Se掺杂Cu2S、Cu2O的第一性原理研究

罗 亮，谢再新，段卓琦，胡永茂，周 豹

（大理大学工程学院，云南大理 671003）

染料敏化太阳能电池（dye sensitized solar cells，DSSCs）一般采用Pt作为对电极，Pt对电极具有良好的导电性和电催化活性，但是抗腐蚀性差且价格昂贵。Cu在自然界中储量丰富，其化合物Cu2S和Cu2O具有较理想的能带宽度和良好的吸光系数，可以替代Pt用于DSSCs的对电极当中。Cu2S、Cu2O作为对电极的缺点是载流子迁移率低，所制备的DSSCs光电转换效率不高，但可以通过掺杂和构建异质结等方式提升材料的稳定性、导电性和催化活性，从而提升太阳能电池的光电转换效率。Yang等〔1〕通过Co掺杂Cu2S制备粉体，检测发现其电催化活性得到了提升。Selopal等〔2〕通过构建异质结Cu2S/Carbon paper对电极，增加了导电性能，也使催化性能更加稳定。Martnez-Ruiz等〔3〕通过模拟研究了金属元素（Ag、Ni、Zn）掺杂对Cu2O性能的影响，并证实Ag掺杂会使Cu2O的带隙减小，而Ni和Zn掺杂会在Cu2O的费米能级附近引入杂质能级，而这些杂质能级会充当载流子复合中心。刘宗斌等〔4〕制备了Mn掺杂的Cu2O，结果发现其光吸收强度和带隙均有增加，光电流增强，光催化活性显著提高。

目前对于Cu2S和Cu2O掺杂或构建异质结复合材料的相关研究不多，并且关于Se掺杂这两类材料的相关研究也很少。本文利用第一性原理计算研究Se掺杂Cu2S和Cu2O的电子结构和光学性质，为Cu2S和Cu2O在太阳能电池电极材料上的应用提供理论参考。

1 计算方法

本研究采用密度泛函理论的量子力学计算方法，即第一性原理计算。

第一性原理的基本思想是：将多原子体系视为由原子核、内层电子和外层自由电子构成的多粒子系统，不需要提供任何经验性参数，只需5个基本常数（光速、电子质量、电子电量、普朗克常数和玻尔兹曼常数），在求解体系薛定谔方程的运算中实现了最大程度上“非经验性”计算〔5〕。

多粒子系统的薛定谔方程可以用以下公式表示：

式中，ħ=h/2π=1.054 5×10-34J·s为约化普朗克常数，ψ与H分别为系统的波函数与哈密顿量。假如粒子间忽略相互作用，其中哈密顿量可以改写为：

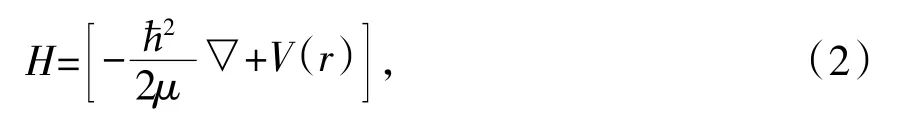
其中μ为粒子的质量，V（r）为外部势场，若考虑粒子间的相互作用，则哈密顿量改写为：

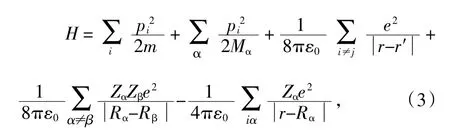
式中，ε0为真空介电常数，m、p、r与e分别为电子的质量、动量、坐标与电荷；而M、P、R与Ze为原子核的质量、动量、坐标与电荷。通过求解体系薛定谔方程的波函数与哈密顿量，可以研究材料的电子结构、光学性质、力学性质等许多物理性质〔5〕。

由于多电子体系计算需要合理的简化和近似，所以计算多电子体系基态通常会转变为单电子体系近似的方法，其中最常用的两种方法分别是Hartree-Fock近似与密度泛函理论（density functional theory，DFT）。其中DFT由Hohenberg等人在1964年首次提出，提出的Hohenberg-Kohn（HK）定理为现代密度泛函理论打下了坚实基础。该定理的核心思想是：体系中的所有物理量都可以通过只包含电子密度的变量来唯一决定，而实现方法是通过变分原理来求得体系基态。但是HK定理中电子密度函数、动能泛函和交换关联能泛函是不确定的，因此具体求解还是无法进行。1965年，Kohn等后续研究得到了Kohn-Sham（KS）方程，即单电子方程：

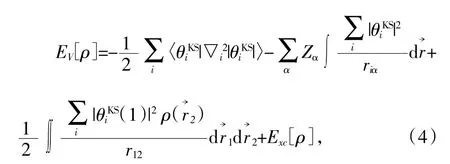
式中，ρ为电子密度，θiKS为K-S轨道，通过求解薛定谔方程得到。等式右边第一项为电子动能，第二项为核与电子的吸引势，第三项为电荷的库伦相互作用，第四项Exc［ρ］为交换关联能。由于KS方程将有相互作用的复杂部分都包含在交换关联能中，所以这一项的精确程度十分重要。

影响DFT计算产生误差的原因有两个：一是交换关联能，对于交换关联泛函通常选用局域密度近似（LDA）、广义梯度近似（GGA）或者混合泛函方法来减小计算误差；二是基组效应，基组效应可以通过扩大基组来减小其计算误差。

经过不断的研究，现代密度泛函理论已经较成熟，具有较高的精度和可接受的计算效率，被广泛用于物理、化学、材料等领域，Kohn也因此在1998年获得了诺贝尔化学奖〔6〕。近年来，基于DFT的计算软件非常多，例如VASP、Material Studio（MS）等，通过计算材料性质为实验提供了较为恰当的预测与验证。其中马骏〔7〕通过MS模拟了GaN光电阴极材料在激活呈负电子亲和势状态时的多种情况，证实了在Ga0.9375Mg0.0625N（0001）表面上难以去除的Ga2O3组分有利于负电子亲和势的形成；Reich等〔8〕通过第一性原理计算了杂质As对白铁矿和黄铁矿的热力学性质有影响；郑江山〔9〕通过MS构建了G/WS2、G/GaN等多种异质结，研究了异质结材料相比单层材料电学性质的变化。

2 计算过程

2.1 模型建立Cu2S属于单斜晶系半导体，空间点群为C2/m，每个原胞由2个-2价S原子和4个+1价Cu原子构成；Cu2O属于立方晶系半导体，空间点群为Pn-3m，每个原胞由2个-2价的O原子和4个+1价Cu原子构成〔10〕。为了通过计算比较Se掺杂前后对Cu2S/Cu2O材料性能带来的改变，本文构建了2×2×2的Cu2S/Cu2O超胞模型，共包含48个原子，其中32个Cu原子，16个S/O原子，然后通过一个Se原子掺杂，替换超胞中的S/O原子，Se在体系中的占比为2.08%。本文将两种Se掺杂模型分别命名为Cu2S-Se与Cu2O-Se，见图1。

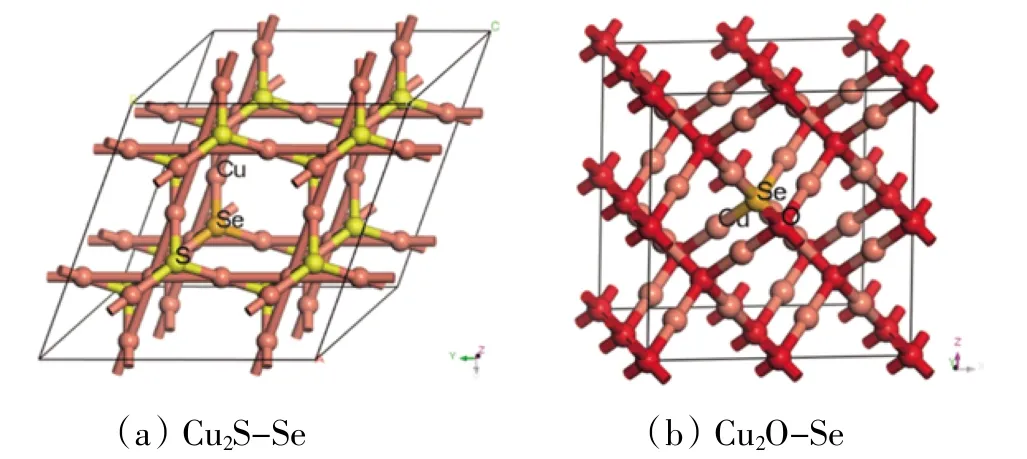
图1 超胞模型

2.2 计算设置在计算之前需要对晶胞进行几何优化，降低晶胞的能量，达到一个稳定的状态结构。计算过程中采用GGA下的PBE泛函确定交换关联能，平面波截断能设置为400 eV，布里渊区的Monkhorst-Pack网格设置为2×2×2。采用Broyden-Fletcher-Goldfarb-Shanno（BFGS）方法进行几何优化，每个原子上的能量收敛值设为1.0×10-5eV/atom，应力偏差小于0.05 GPa，离子力低于0.03 eV/Å，公差偏移小于1.0×10-3Å。计算中选取的原子价电子为Cu 3p63d104s1，S 3s23p4，O 2s22p4，Se 4s24p4。几何优化之后，计算所得的晶格常数与文献中的数据〔11〕基本一致，见表1。

表1 Cu2S和Cu2O晶格参数优化结果

3 计算结果分析

3.1 能带结构与态密度分析Cu2S掺Se前后的能带结构和态密度见图2。从图2（a）中可以看出，零点处为费米能级，计算能带结构时默认的高对称点为（G F Q Z G），导带的最低点与价带的最高点都在G点，证明Cu2S为直接带隙的p型半导体。计算所得的带隙值为1.204 eV，与文献报道的Cu2S带隙在1.21 eV左右基本符合〔12〕。与本征Cu2S相比较，从图2（b）中可以看到，由于杂质Se的掺入，价带变化不大，而导带底向下偏移，带隙值下降为1.008 eV。从图2（c）可以看到Cu2S的总态密度（TDOS）和分态密度（PDOS）。由图可知，Cu2S的价带可以分为-14～-12 eV的下价带和-6.5～0 eV的上价带。下价带主要由S的3s轨道贡献，上价带主要由S的3p轨道和Cu的3d轨道贡献，最主要的还是由Cu的3d轨道贡献。导带部分主要由Cu的3p轨道、4s轨道和S的3p轨道杂化形成。图2（d）为Se掺杂Cu2S的态密度分布，与本征Cu2S的TDOS走势基本相同，但是PDOS可以看到由于Se的4p轨道主要贡献在-6～0 eV和1～3.5 eV这两个部分，都在费米能级处附近，导致了带隙的减小。并且Se的4s轨道还在-14～-12 eV处与S的3s轨道发生了杂化，使底部存在更多的剩余电子。

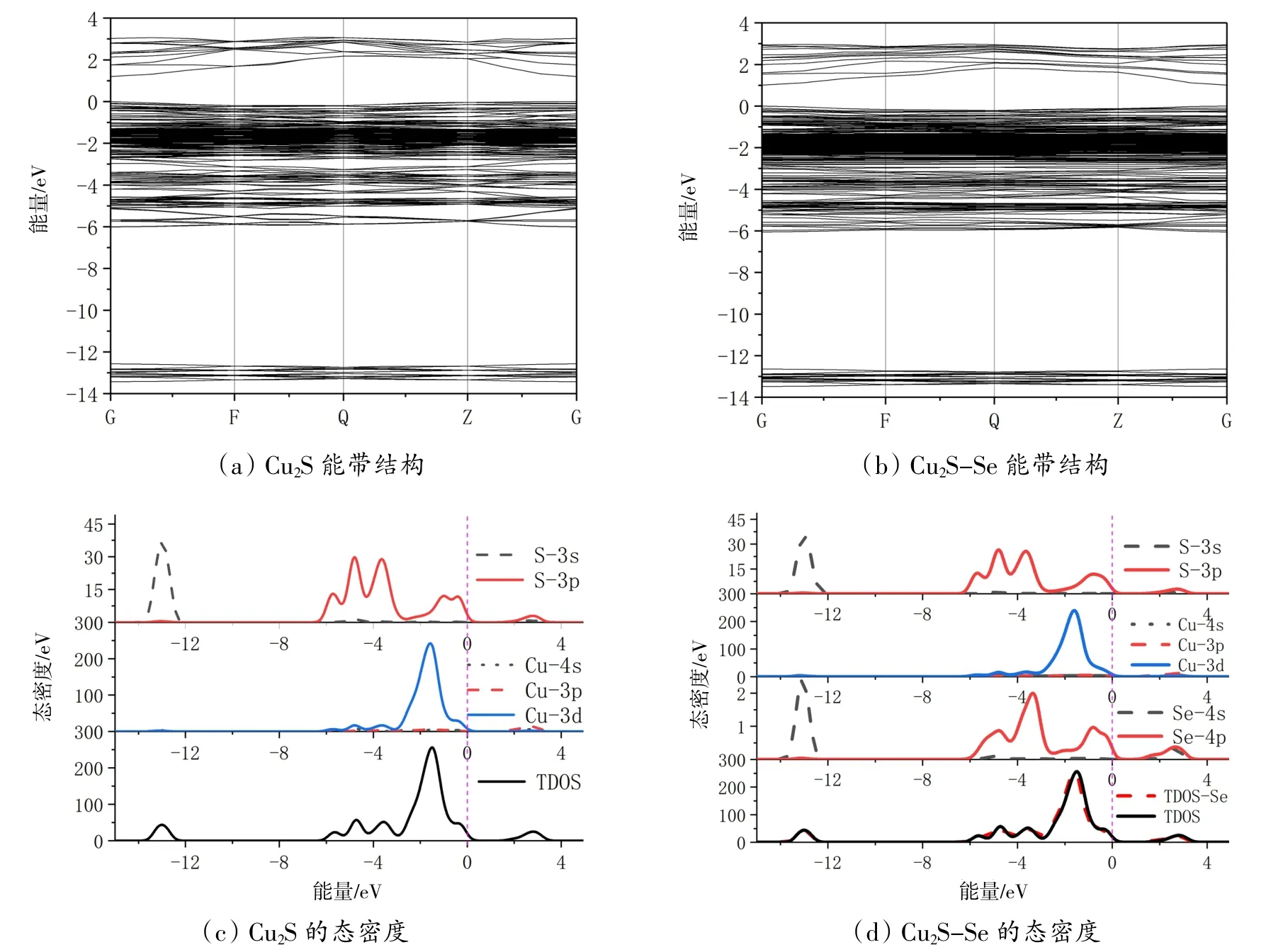
图2 Cu2S掺Se前后的能带结构和态密度

Cu2O掺Se前后的能带结构和态密度见图3。从图3（a）中可以看出Cu2O也是直接带隙的p型半导体。计算所得的带隙值为0.551 eV，与文献报道〔13〕的Cu2O带隙基本相同，但是实验公布的值为1.8～2.2 eV〔14〕，这是由于计算过程中高估了Cu的3d轨道能量的缘故，还有就是在解KS方程时并不会考虑体系的激发态的原因〔5〕。为了计算值和实验值一致，本计算设置了一个1.65 eV的修正值，修正后的带隙值为2.201 eV。从图3（b）中可以看到，由于杂质Se的掺入，与本征Cu2O的能带结构相比较，价带出现了多处杂化，价带向低能端移动，导带向高能端移动，带隙值升高为2.328 eV。从图3（c）可以看到Cu2O的态密度分布。由图可知，Cu2O的价带可以分为3个部分：-21～-18 eV的下价带由O的2s轨道贡献，-7.5～-3.5 eV的中价带由O的2p轨道和少量的Cu的3d轨道贡献，-3.5～0 eV的上价带由Cu的3d轨道和少量的O的2p轨道贡献。导带部分主要由Cu的3p轨道、3d轨道和O的2p轨道杂化形成。在图3（d）中，Se掺入后对于Cu的轨道影响不是很大，但是使得O的轨道峰强降低了30%多，并且使O的轨道价带部分发生了左移，即向低能端移动，导带部分发生了右移，即向高能端移动。由于Se的掺入导致O的轨道偏移，才使带隙增大，上述结论进一步得到了证实。Se的4s轨道在-15～-13.5 eV出现了一个峰值为2.7 eV的小峰，Se的4p轨道主要贡献在-8～-3 eV这部分，在费米能级处附近有少量的贡献。

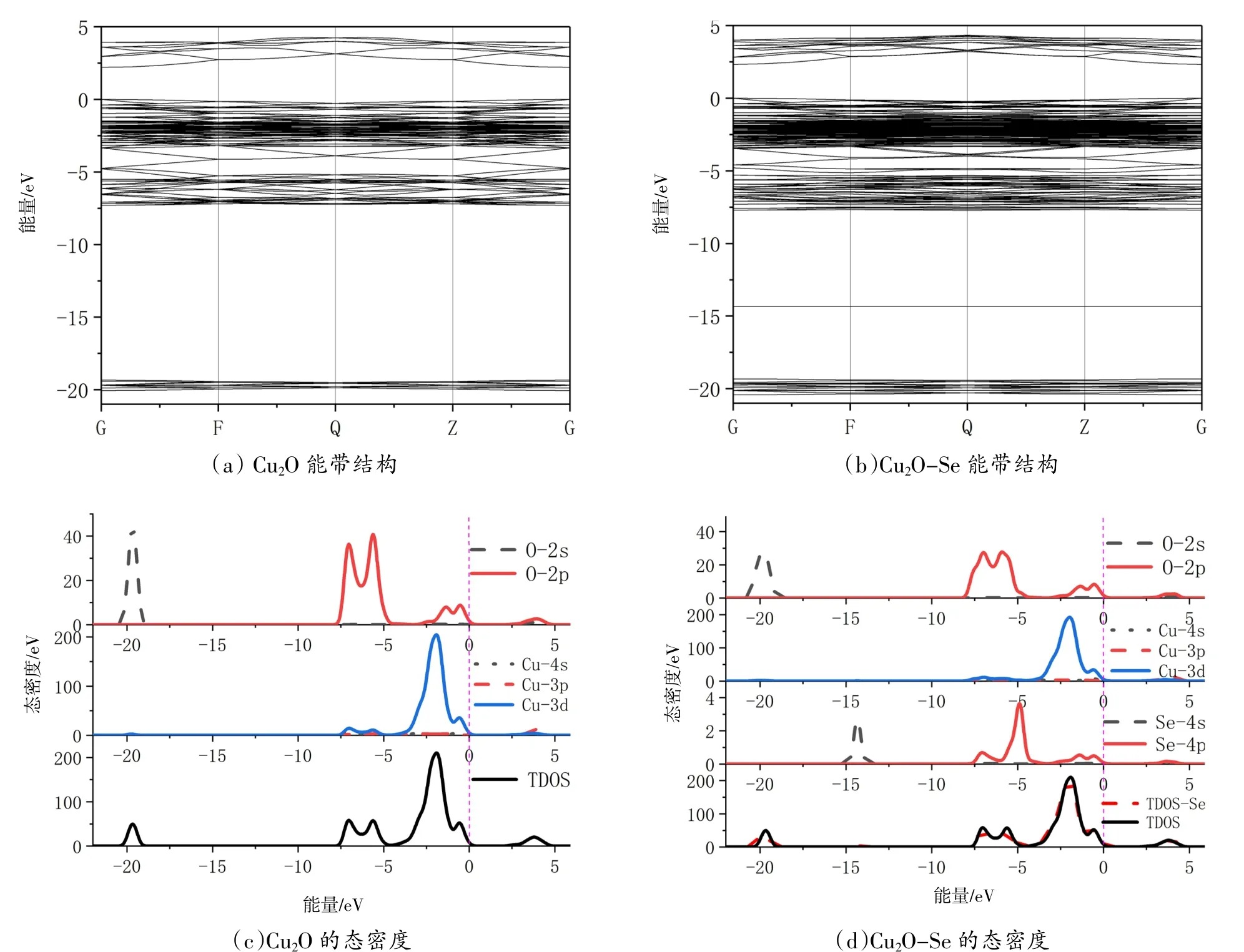
图3 Cu2O掺Se前后的能带结构和态密度

3.2 Mulliken原子布居分析计算中选取的原子价电子为Cu 3d104s1，S 3s23p4，O 2s22p4，Se 4s24p4。表2给出了Cu2S掺杂前后的价电子布居数，结合Cu2S的态密度图看出在掺杂之前价电子主要从Cu的3d轨道向S的3p轨道跃迁，下面的光学性质分析也对此进一步进行了证明。从表2还可看出，Cu原子和S原子之间只存在较强的离子键，当Se掺入之后，原子间的离子键变弱，其临近的Cu原子从失去0.26个电子降到失去0.18个电子，次临近的S原子从得到0.37个电子升到得到0.32个电子。

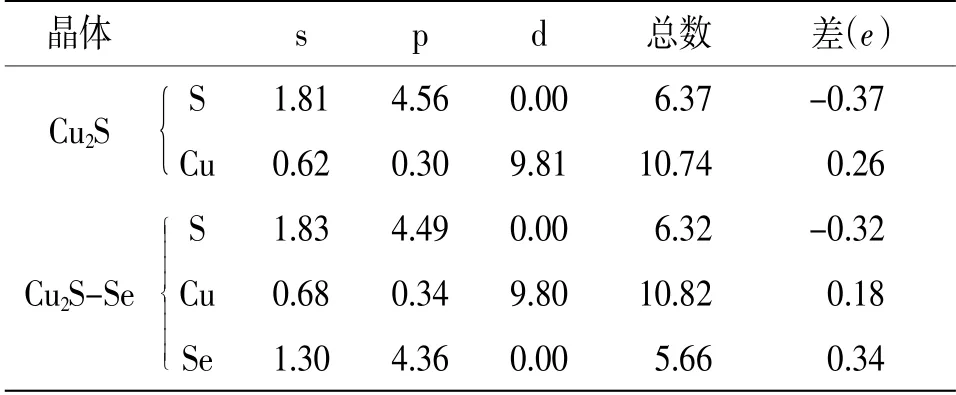
表2 Cu2S掺Se前后的Mulliken电荷

表3给出了Cu2O掺Se前后的最外层电子布居数，本征Cu2O价电子主要从Cu的3d轨道向O的2p轨道跃迁，Cu原子和O原子之间存在共价键，但是当Se掺入之后，Se原子失去1.61个电子，相邻的Cu原子得到0.01个电子，次相邻的O原子得到0.68个电子。说明掺入Se之后，至少存在一个自由电子，使Cu2O呈现金属化〔5，10-11〕。自由电子的存在让Cu2O材料内的自由电子密度增加，改善Cu2O电子传输能力较差的特性，提升其导电性能。

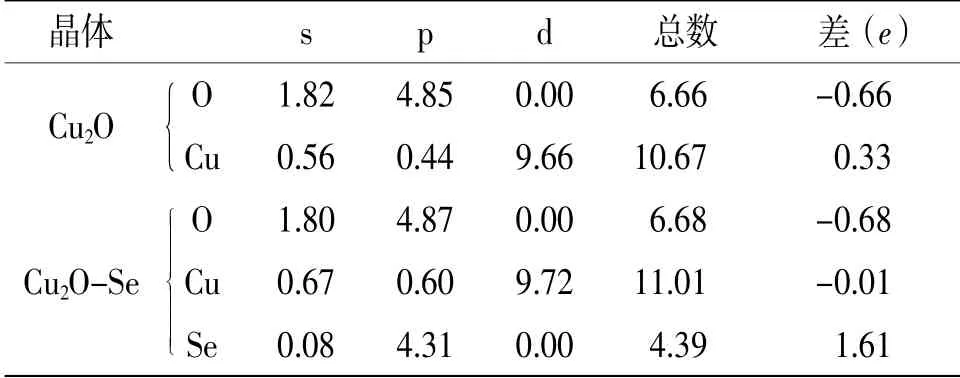
表3 Cu2O掺Se前后的Mulliken电荷

3.3 光学性质分析光学性质的表征可以通过计算复介电函数、光反射率和光吸收系数等参数，这些参数对半导体材料用作太阳能电池电极有着重要的意义。其中复介电函数ε（ω）和光吸收系数α（ω）可以表示为：

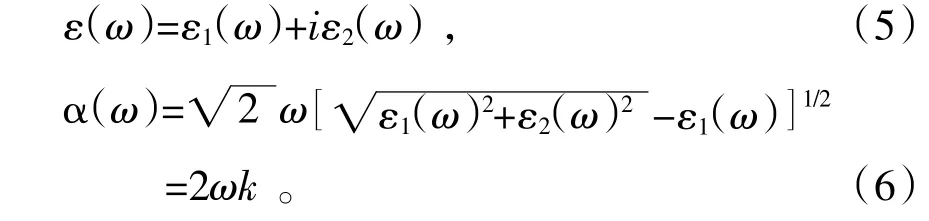
图4是Se掺入前后Cu2S的复介电函数、光反射率。如图4（a）所示，由Cu2S的介电函数实部ε1可知静介电函数为4.1，Cu2S的介电函数实部ε1随着光子能量的增大而增大，根据柯喇末-克罗尼格色散关系〔10〕可知在1.7 eV处能量达到最大，表现为正常色散，然后开始随着光子能量的增大而减小，表现为反常色散。Cu2S的介电函数实部ε1有1.7 eV和6.2 eV两个峰。1.7 eV主要由Cu的3d轨道和S的3p轨道之间电子跃迁引起的，6.2 eV主要由Cu的3p轨道、4s轨道和S的3p轨道之间的电子跃迁引起的。并且光子能量在3.5 eV到5.2 eV和7.8 eV到8.5 eV波段介电常数为负值，与图4（b）光反射率最高两处峰相对应，表面光子在此阶段无法在Cu2S中传播，呈现金属反射特性，反射率的提高有利于将光阳极没有吸收的光反射回去，增加光的利用率。掺Se以后静介电函数增大，同时反射率也有略微的增大，这都有利于对入射光的吸收和电子的跃迁〔15〕。

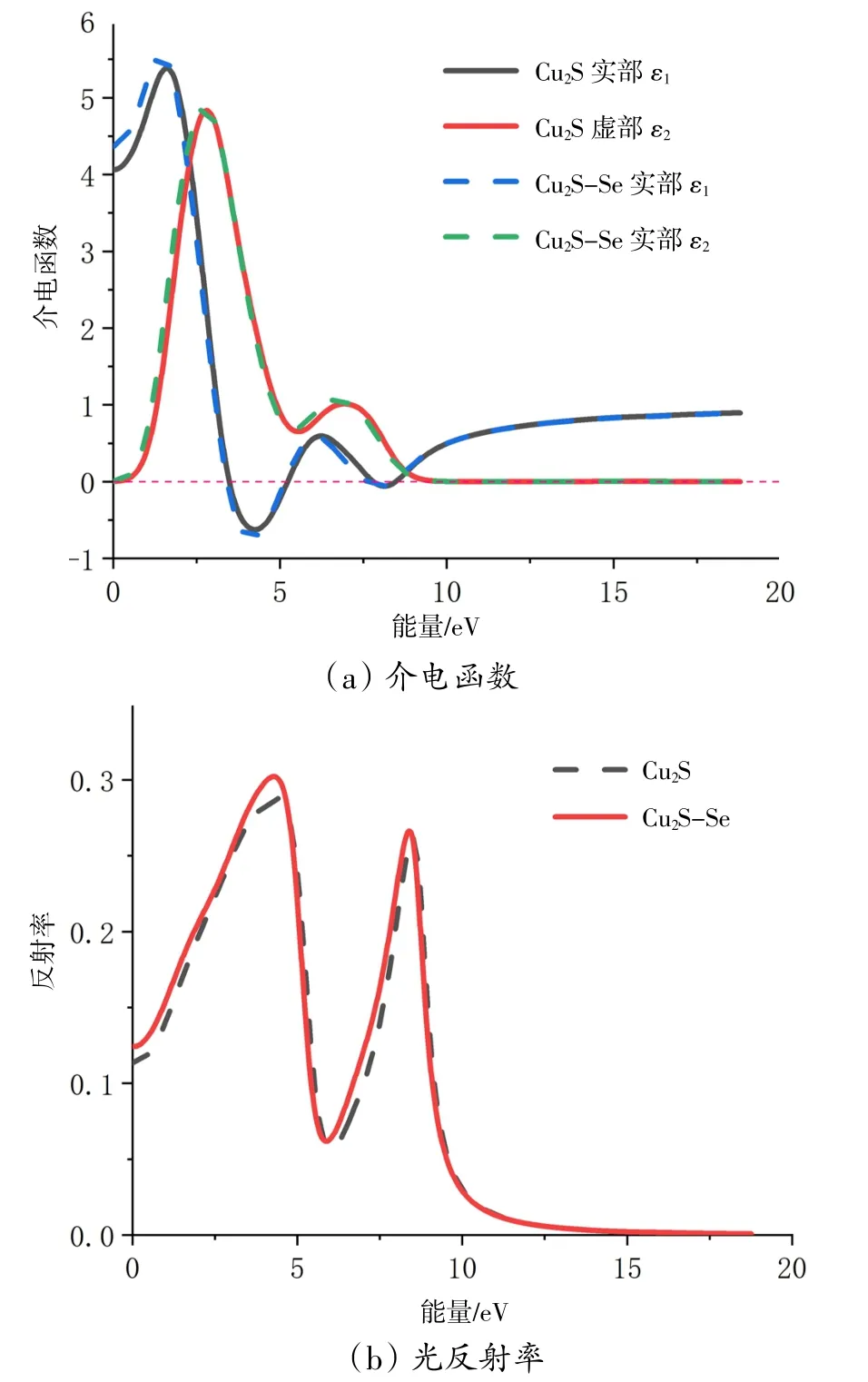
图4 Cu2S掺Se前后的介电函数和光反射率

光吸收系数决定在一个给定波长下光在被吸收之前能在材料中行径的距离。由图5可知，本征Cu2S在163 nm第一个峰处吸收系数为7.71×104cm-1，在309 nm最高峰处吸收系数为8.15×104cm-1。在Se掺杂后，吸收边发生略微的红移，吸收系数也略有提高，对于紫外光（400 nm以下）和可见光（400～760 nm）的吸收都有一定的提升，吸收光效果小幅度提升。

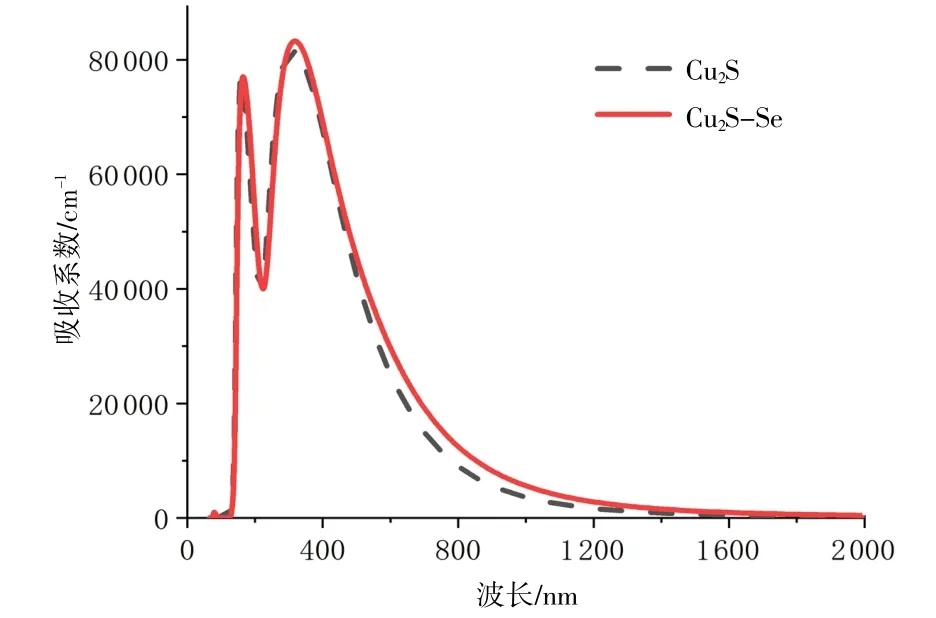
图5 Cu2S掺Se前后的吸收光谱

Se掺杂前后Cu2O的介电函数和光反射率见图6。由图6（a）可知，掺Se后Cu2O的静介电常数由6.1增加到7.1，介电函数实部也随着光子能量的增大而增大，在3.0 eV处能量达到最大，呈正常色散，然后开始随着光子能量的增大而减小，呈反常色散。整体性质的趋势与Cu2S相似。

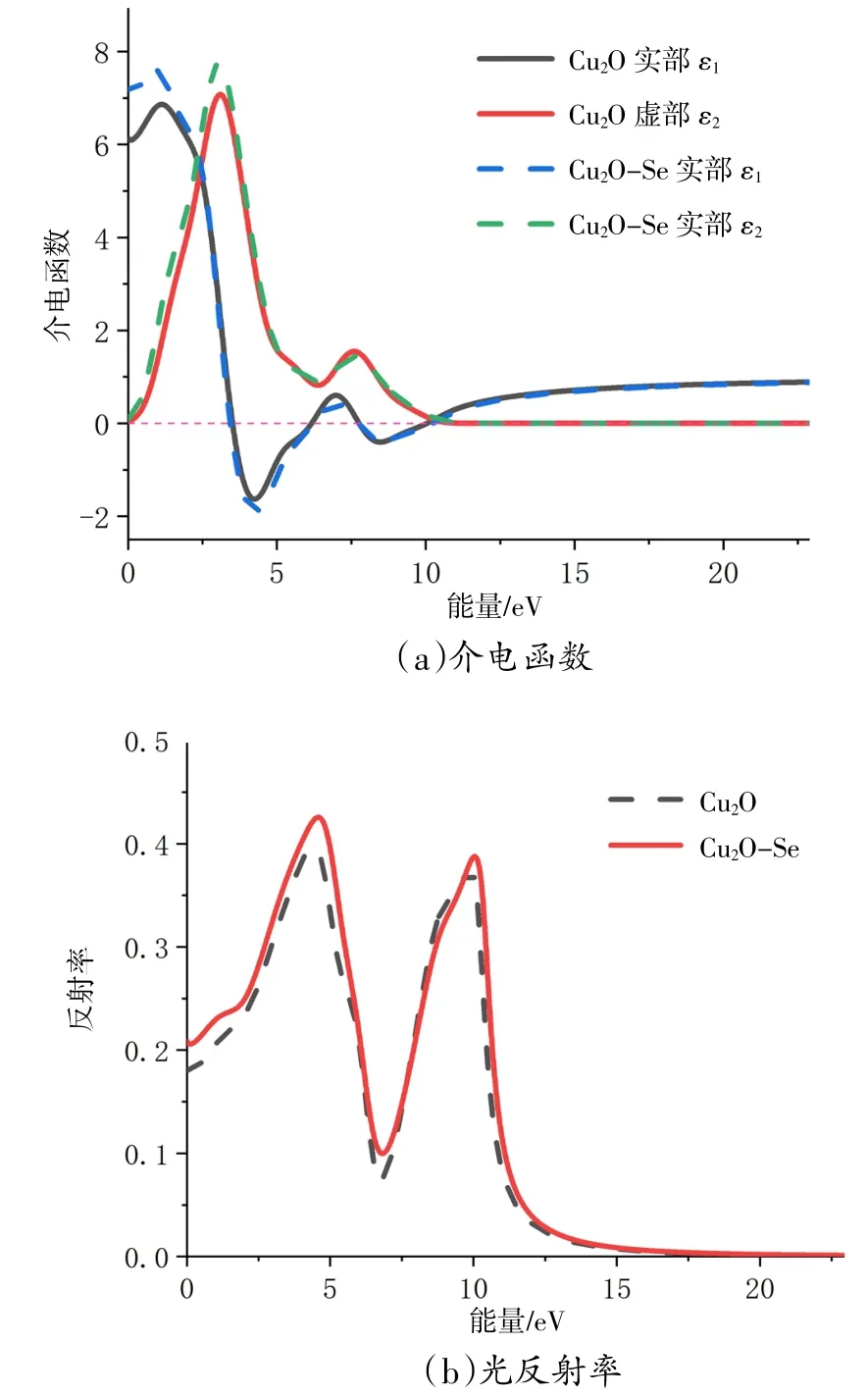
图6 Cu2O掺Se前后的介电函数和光反射率

Cu2O掺Se前后的吸收光谱见图7。由图7可知，掺杂后Cu2O在第一个峰附近吸收系数有所降低，从152 nm处的1.17×105cm-1降低到153 nm处的1.14×105cm-1，但在最高峰附近302 nm处的1.13×105cm-1吸收系数提升为298 nm处的1.19×105cm-1，并且吸收宽度也有扩展，总体吸收光效果略有增强。

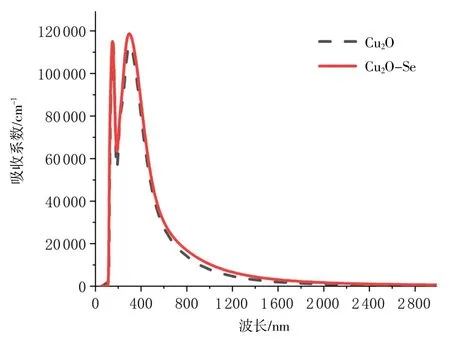
图7 Cu2O掺Se前后的吸收光谱

4 结论

本文研究了Se分别掺入Cu2S和Cu2O后材料电学性质的改变，受Se的4s轨道的影响，Cu2S的带隙从1.204 eV降低到1.008 eV，同时Se使Cu、S原子间的离子键变弱，反射率增强，但是光吸收系数有所提高。总体来说掺杂Se后的Cu2S性能提升并不明显，掺杂Se后的Cu2O在带隙、电子传输、光吸收系数等方面都有所提升。为探索Se掺杂Cu2S和Cu2O作为太阳能电池对电极的研究提供理论支持。