香蕉树的 指标和 指标的显式公式
2022-01-18杨利民
杨利民
(大理大学数学与计算机学院,云南大理 671003)
在文献〔1〕中,通过覆盖方法推出S(n)-因子的计数的分支分析法,分支分析法实际是一种递归计数方法,只不过是以完全图作为分支的计数方法。在文献〔2〕中,利用分支分析法,获得四叶树的Hosoya指标。在文献〔3-4〕中,得到Merrifield-Simmons指标的递归计数方法,它是第二种分支分析法。在这篇论文中,我们分别采用两种分支分析法〔1,4〕,获得香蕉树的Hosoya指标和Merrifield-Simmons指标的显式公式,它们是化学图论中两个重要的拓扑参数,对组合化学具有重要价值和实际意义〔5-7〕。
1 定义和引理
1.1 定义定义1 令S(n)={Ki:1≤i≤n},n≥1,并且Ki是有i个顶点的完全图,如果M是图G的一个子图,且M的任意分支都同构于S(n)={Ki:1≤i≤n}的某一元素,那么M叫做图G的一个S(n)-子图,如果M是图G的一个生成子图,那么M叫做图G的一个S(n)-因子〔1〕。
恰有k个分支的S(n)-因子的个数记为N(G,k),S(n)-因子的所有个数记为A(G)。
定义2 图G的所有k-匹配个数,包括空集,称作Hosoya指标。Hosoya指标用Z(G)表示〔2〕。
定义3 图G的所有独立集的个数,包括空集,称作Merrifield-Simmons指标,用i(G)表示〔3〕。
1.2 基本引理第一种分支分析法如下:
引理1 对于图G的给定一点P,如果过给定点P的完全图是Ki1,Ki2,…,Kir,ij∊[1,n],1≤j≤r,n是G的顶点数,于是G的所有S(n)={Ki:1≤i≤n}-因子个数:

其中A(G-V(Kij))是删除V(Kij)和与V(Kij)相关联的边〔1〕。
引理2 假设G1,G2,...,Gt是图G的t个分支〔1〕,那么
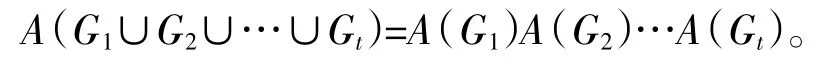
引理3 假设K1,n是n+1个点的星形图,那么A(K1,n)=n+1。
证明:因为K1,n是n+1个点的星形图,所以
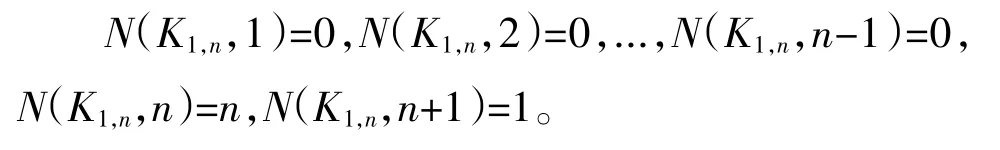
从而A(K1,n)=N(K1,n,1)+N(K1,n,2)+…+N(K1,n,n-1)+N(K1,n,n)+N(K1,n,n+1)=0+0+…+0+n+1=n+1。
引理4 假设图G的顶点数为n并且无K3子图,那么Hosoya指标Z(G)等于图G的所有S(n)-因子的个数:Z(G)=A(G)〔2〕。
第二种分支分析法如下:
引理5 如果v∊V(G),那么i(G)=i(G-v)+i(G-NG[v]),其中v在G中的邻域记为NG(v),并且NG[v]=v∪NG(v)〔4〕。
引理6 假设G1,G2,…,Gt是图G的t个分支〔4〕,那么
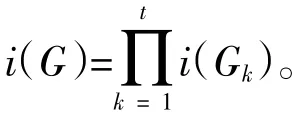
引理7 假设K1,n是n+1个顶点的星形图,那么i(K1,n)=2n+1〔4〕。
2 主要结果
2.1 香蕉树的Hosoya指标的显式公式假设K1,n1,K1,n2,…,K1,nk是一族互不相交的星形图,V(K1,ni)={ci,ai1,ai2,…,aini},并且deg(ci)=ni,1≤i≤k。一棵香蕉树BT(n1,n2,...,nk)是这样一棵树,通过增加一个新的顶点o,并把它连接到a11,a21,…,ak1上,所得到的树〔8〕。
定理1 假设图G是一棵香蕉树BT(n1,n2,…,nk),如图1,那么它的S(n)-因子的所有个数:

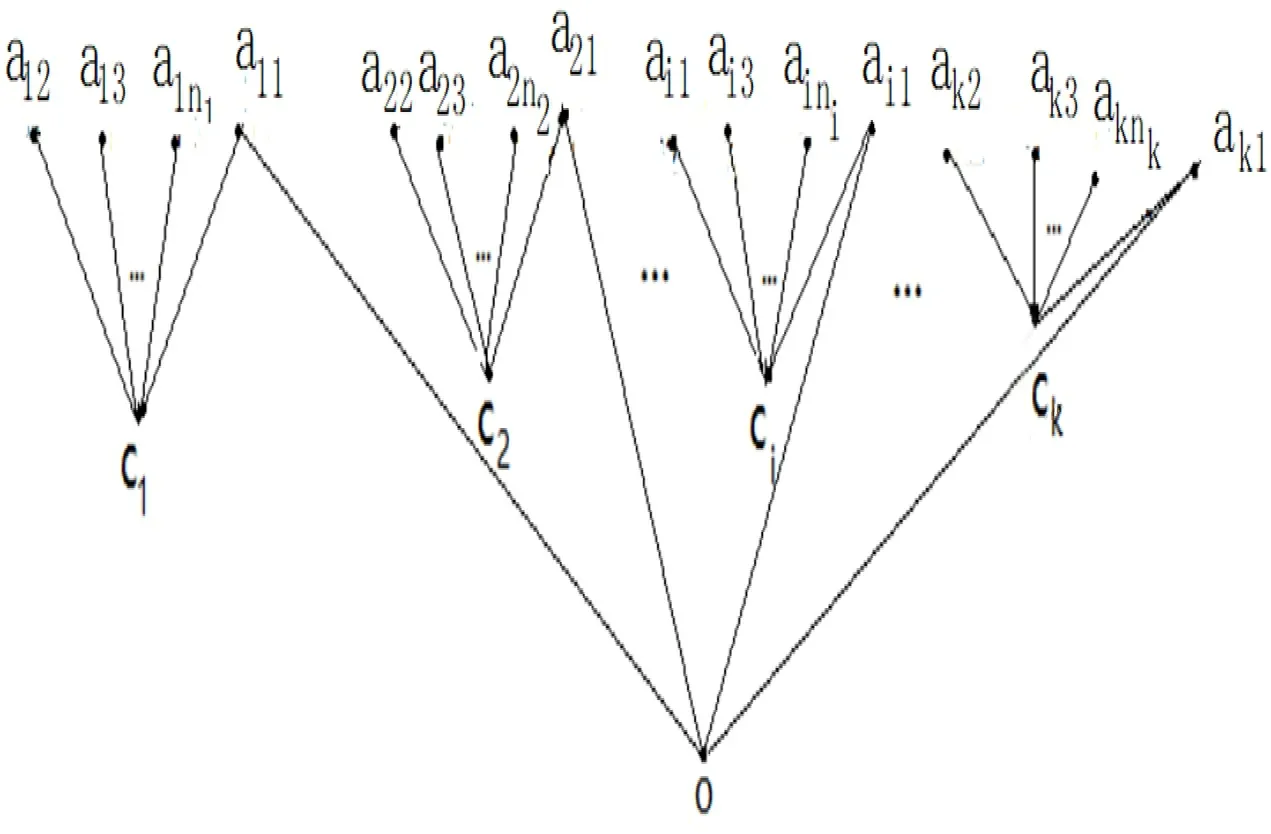
图1 香蕉树BT(n1,n2,...,nk)
证明:因为G是一棵香蕉树BT(n1,n2,...,nk),它是特殊的一棵树,所以香蕉树无K3子图,它也就没有K4,K5,…,Kn子图。利用第一种分支分析法,对固定点o进行分析,过o点的完全图只有点K1和k个K2,即点o和边oa11,oa21,…,oak1。讨论分2种情况:
情况一 过o点的完全图为K1,作为一个分支,则S(n)-因子个数如下:
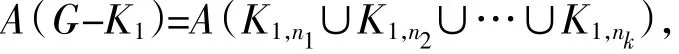
根据引理2得到

根据引理3就有
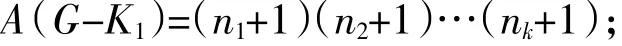
情况二 过o点的完全图为oa11,oa21,...,oak1,这k个完全图K2是对称的,K2作为两个点的完全分支,则

综上所述,根据引理1,于是

以致有
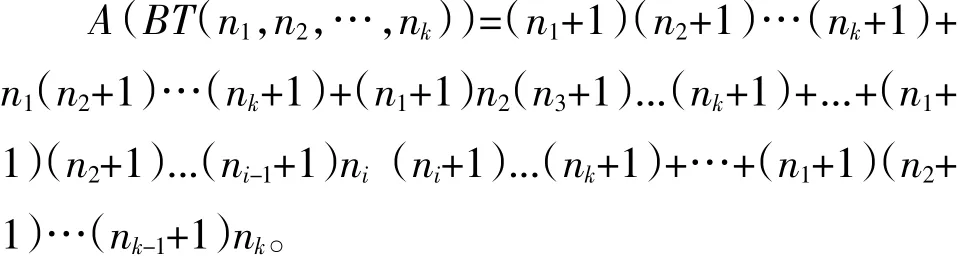
定理2 如果图G是一棵香蕉树BT(n1,n2,…,nk),则它的Hosoya指标
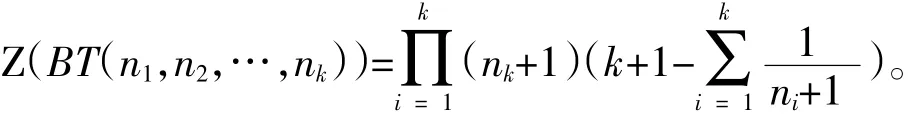
证明:因为G是一棵香蕉树BT(n1,n2,…,nk),它是特殊的一棵树,所以香蕉树无K3子图。
根据引理4,于是
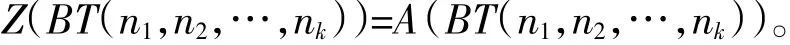
再根据定理1,得到
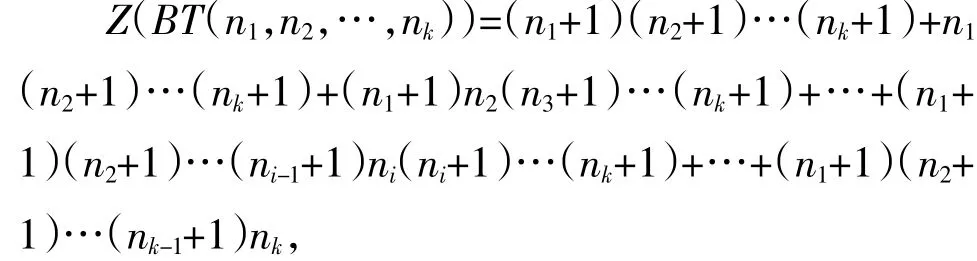
从而有
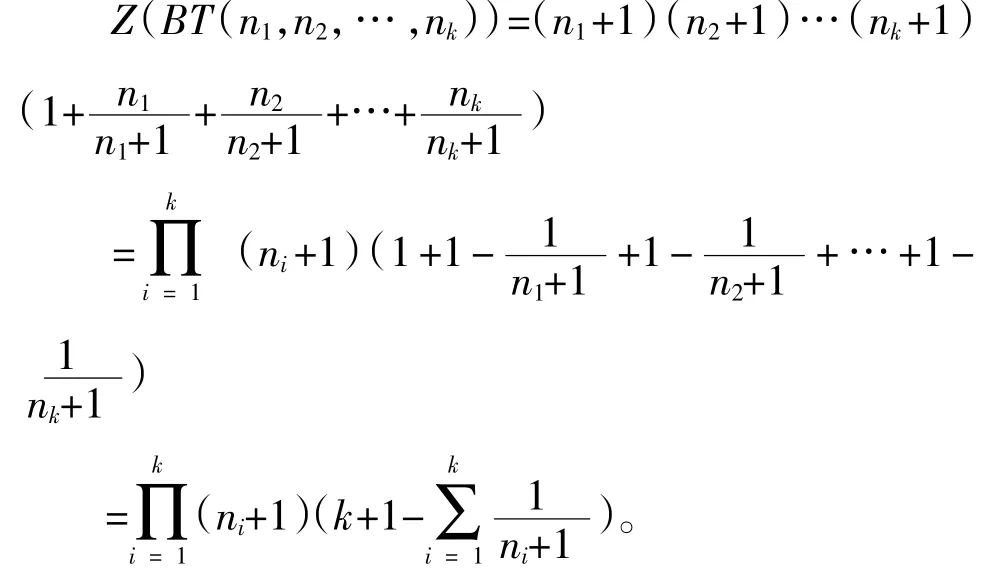
推论1 如果图G是一棵香蕉树BT(n,n,…,n),n的个数是k,则它的Hosoya指标

证明:结论来自定理2,证明略。
例1 假设图G是香蕉树BT(3,3,3,3),如图2,则它的Hosoya指标
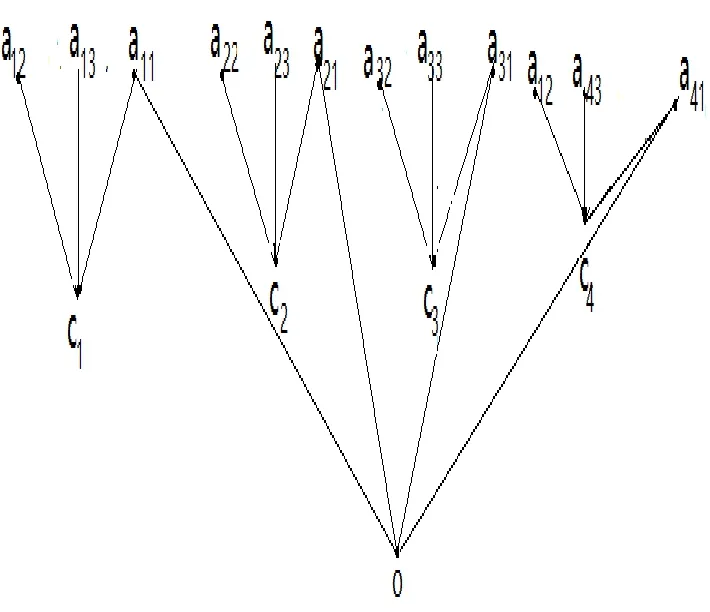
图2 香蕉树BT(3,3,3,3)
Z(BT(3,3,3,3))=1 024。
证明:因为图G是香蕉树BT(3,3,3,3),所以n=3,k=4。
根据推论1,于是
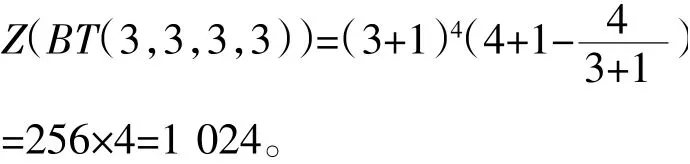
2.2 香蕉树的Merrifield-Simmons指标的显式公式
定理3 如果图G是一棵香蕉树BT(n1,n2,…,nk),则它的Merrifield-Simmons指标
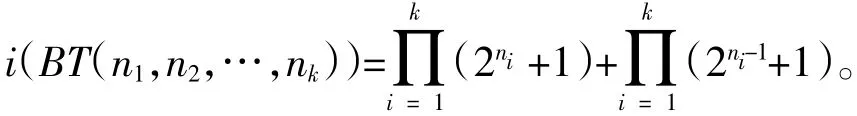
证明:利用第二种分支分析法,在图1中,对o点进行分析,根据引理5,于是
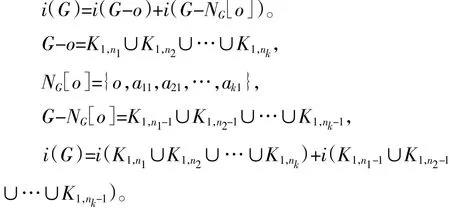
根据引理6,我们有
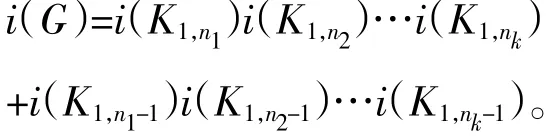
通过引理7,从而

推论2 如果图G是一棵香蕉树BT(n,n,…,n),n的个数是k,则它的Merrifield-Simmons指标
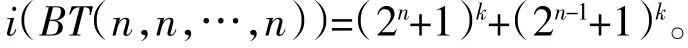
证明:结果来自定理3,证明略。
例2 假设图G是香蕉树BT(3,3,3,3),如图2,则它的Merrifield-Simmons指标

证明:因为图G是香蕉树BT(3,3,3,3),所以n=3,k=4。
根据推论2得到
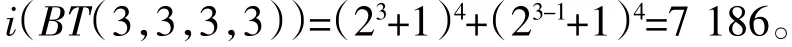
本文分别采用两种分支分析法,得到香蕉树的Hosoya指标和Merrifield-Simmons指标的显式公式,这些结果对化学图论是有价值和实际意义的。
