舰载机/发动机一体化控制着舰复飞动态特性研究

冯玉博，李 冬，姚明智，欧阳文恒，陈浩浦，刘志远

(1.92728部队，上海 200040；2.91899部队，辽宁 葫芦岛 125001；3.海军装备部驻九江地区军事代表室，江西 九江 332000)

1 引言

为提高舰载机的复飞成功率和生存率，需要对舰载机复飞技术进行研究。在众多研究方法中，舰载机飞行仿真简单实用，其计算结果准确可信，还可节省大量的人力物力。特别是在确定复飞边界条件以及模拟飞行训练难以出现的情况时，仿真作用尤为突显。建立精确的舰载机飞/发一体化模型，模拟实际中所处的各种环境和运动，通过加速控制规律设计技术，可提高发动机的加速性能并最终提高舰载机的复飞成功率。

针对舰载机仿真可供收集、研究的国外资料较少，但从有限的公开文献看，其对舰载机复飞能力很重视，且研究得很深入[1-3]。我国的舰载机处于发展阶段，各相关工业部门及院校对舰载机技术开展了大量的工作，特别是针对舰载机复飞性能进行了广泛的研究。如考虑甲板风速和航母在海面上运动等对舰载机的影响，建立了舰载机飞行运动模型；采用牛顿运动定律描述舰载机的运动，通过受力关系求解坐标系下的方程组得到各个变量的约束关系[4-5]。在飞行模拟中加入发动机模型，对发动机加速控制规律进行优化；按照基于飞/发一体化约束的舰载机设计思路，对建立结合舰载机自身特点并考虑发动机推力的舰载机复飞运动模型进行研究[6-9]。

本文基于发动机动态模型和舰载机气动模型，以舰载机复飞过程为任务剖面，依据能量法建立了可准确表述舰载机动态特性的飞/发一体化模型，并给出了复飞时发动机的供油和控制规律。通过飞/发一体化模型得到的舰载机复飞时着舰重力、所需甲板长度和着舰时甲板风速等参数的关系，可为保证舰载机成功复飞提供参考。

2 发动机动态模型

按照气体流经发动机部件的顺序，建立了发动机部件级模型[10-11]。图1为发动机总体结构示意图。

图1 发动机结构Fig.1 General structure of engine

发动机处于加速或减速状态时，需考虑其容积效应。此时，功率平衡方程为：

式中：MT、MC分别为流经涡轮和压气机的气体质量流量，ΔST、ΔSC分别为涡轮和压气机的焓值变化量，N为转速，HPext为剩余功率。

动态流量连续方程为：

式中：Mout、Min分别为出口和进口气体的质量流量，γ、R、J、p、K分别为比例系数，气体常数，气体体积、压力，温度。

动态能量方程为：

式中：hout、hin分别为出口和进口气体的焓值，u为流速。

在给定加、减速控制规律的条件下，上述微分方程中的微分项均采用隐式欧拉格式进行差商求解，求解步长可适当增大。

3 舰载机飞/发一体化控制动态特性模型

如图2所示，如果把舰载机看作一个运动质点，并假设发动机安装推力T和气动阻力(D+Z)(D为带正常外挂物的舰载机阻力，Z为由起落架、非正常外挂物或阻力伞等突出部分引起的附加阻力之和)作用在与舰载机速度V同一个方向上，则对其进行受力分析后运用能量法，可得到起飞推力载荷TSL/W(TSL为海平面发动机安装推力，W为舰载机所受重力)和机翼载荷W/S(S为机翼面积)的主方程：

图2 飞机受力示意图Fig.2 Schematic diagram of aircraft force

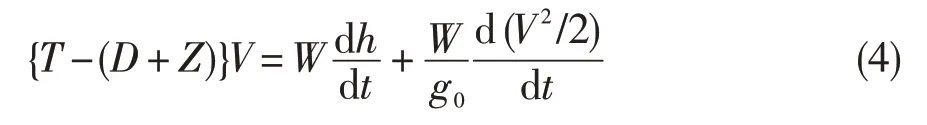
式中：h为高度，dh/dt为高度变化率，g0为重力加速率。

为便于对舰载机和发动机进行一体化评估分析，采用式(4)的无因次形式：

式中：ze=h+V2/2g0，为舰载机的瞬时单位机械能(势能和动能之和)。

式(5)两边乘以V可得单位剩余功率：

速度变化率dV/dt是舰载机的主要特征参数，Ps具有速度的单位。假设发动机安装推力由式(7)给出：

式中：α为推力变化率，取决于飞行高度、速度和发动机工作状态。

舰载机所受重力由式(8)给出：

式中：β为瞬时重力比，取决于舰载机消耗的燃油和投放的有效载荷；WTO为舰载机的最大起飞重力。

将式(5)～(8)合并，得到：

根据图2所示，舰载机的升力和阻力表示为：

式中：n为载荷因子，q=为动压头，CL为升力系数，CD为阻力系数。则，

对一般常规布局舰载机，极曲线表达式为：

式中：K1、K2为比例系数，CDO为零升阻力系数。

将式(9)～(13)代入推重比的表达式有：

舰载机在任务剖面的每一点式(14)都成立。式(14)即为舰载机和发动机评估分析的一般表达式，在飞行各航段提出明确的技术指标，即可得到相应航段的评估方程。

4 舰载机着舰复飞典型阶段评估分析

进行航段评估分析前，需先确定舰载机飞行的典型评估剖面，见图3。

图3 舰载机典型着舰剖面Fig.3 Typical landing profile of carrier aircraft

4.1 等速下降航段

舰载机着舰的第一个航段为等速下降航段。给定条件为：dh/dt=-4.14 m/s，V=601.9 km/h，dV/dt=0，h=300 m，n=1。这些数据代入式(14)可得到等速下降航段的表达式：

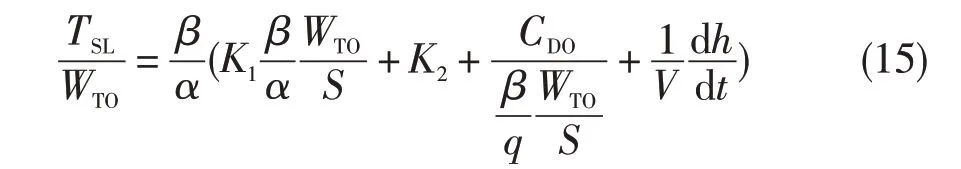
4.2 减速转弯航段

减速转弯航段，舰载机飞越舰首后开始180°的转弯飞行，并不断降低飞行速度。给定条件为：V=485.0 km/h，dV/dt=-1.28 m/s2，h=300 m，转弯半径Rc=1 250 m。在水平等速盘旋情况下，升力的垂直分量与重力平衡，升力的水平分量提供向心力，如图4所示。可得出：

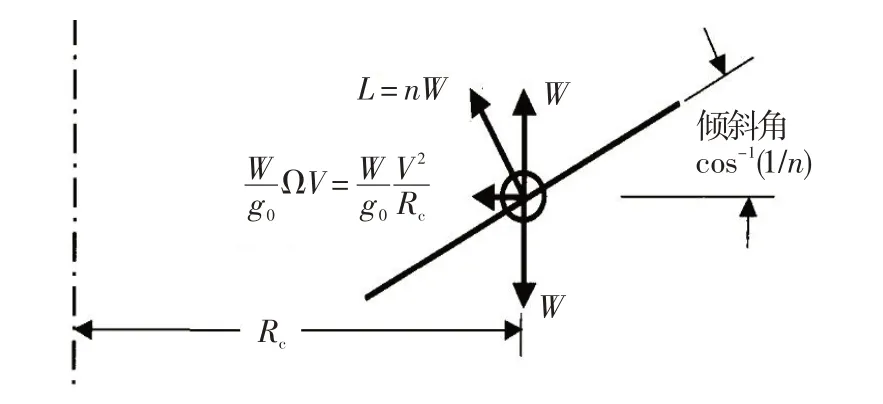
图4 转弯航段舰载机受力分析Fig.4 The force acting on the aircraft in hover

将上述数据代入式(14)，得：

此后，舰载机继续完成水平飞行、转弯、最后进场的等角下滑、触舰滑跑、加速爬升，其计算过程类似。至此，舰载机经历了一个完整的进近着陆和复飞过程。其中，在触舰滑跑航段，舰载机以一定初速度着舰滑跑，最后一个阻拦装置到斜角甲板末端的甲板长度是与复飞性能相关的因素。表1给出了不同航母最后一个阻拦装置到斜角甲板末端的跑道距离。

表1 最后一个阻拦装置到斜角甲板末端的跑道距离Table1 Deck length from the last barrier to the end of angled deck

5 发动机最大状态控制规律

舰载机复飞时，发动机需处于最大状态，在任何飞行条件下最大限度地挖掘潜力，以获得最大推力[12]。基于此，设计了发动机的最大状态控制规律，并表示成以发动机进口总温为变量的函数。所设计的最大状态控制规律见图5，具体如下：

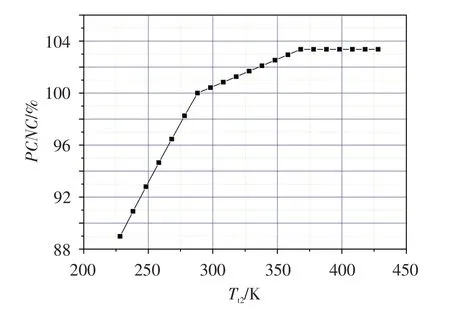
图5 发动机的最大状态控制规律Fig.5 Maximum state control law of engine

(1) 当风扇进口总温Tt2小于288.15 K 时，高压压气机换算转速CNC=100%CNCmax(CNCmax为高压压气机最大换算转速)。此时，高压压气机相对转速PCNC=PCNCdes(PCNCdes为高压压气机设计点相对转速)。

(2) 当风扇进口总温从288.15 K 增加到363.15 K 时，保持CNC=100%CNCmax不变，此时高压压气机相对转速将增加(小于高压压气机最大相对转速PCNCmax)——通过提高涡轮进口总温实现。将涡轮进口总温的最大值设计在较高的发动机进口总温的基础上，是为了提高发动机在较高进口总温时的推力，使得舰载机具有更好的机动性。通常，将最高涡轮进口总温与设计点涡轮进口总温的比值称为节流比(相当于在设计点给涡轮进口总温留有一定的温度裕度)，节流比越高，发动机的高速特性就越好。经过分析，本文取发动机节流比为1.054。

(3) 风扇进口总温大于363.15 K 后，采用高压压气机相对转速保持最大的控制规律，即PCNC=100%PCNCmax。

6 舰载机飞/发一体化控制算例

6.1 舰载机/发动机任务分析

研究舰载机复飞，要求复飞时的发动机状态为85%高压转速加速至最大状态。为此，设计的供油规律为sfcfb=sfcfb,85%+0.628t(sfcfb为耗油率，sfcfb,85%为85%高压转速状态的耗油率)，h=0 km，飞行马赫数为0.147，基于建立的飞/发一体化控制模型，获得的发动机加速性能(推力和耗油率)如图6所示。

图6 舰载机复飞阶段的加速特性仿真Fig.6 Simulation of engine acceleration characteristics of carrier aircraft reflying

基于舰载机飞/发一体化控制模型，计算得到舰载机在不同飞行航段内的结果，见表2。由于舰载机着舰前进场流程各航段所消耗的燃油量并不大，不能通过该阶段直接调节着舰重力。如舰载机重力过大需对其进行调节，可在该阶段通过抛洒燃油等方式进行，从而满足着舰重力要求。

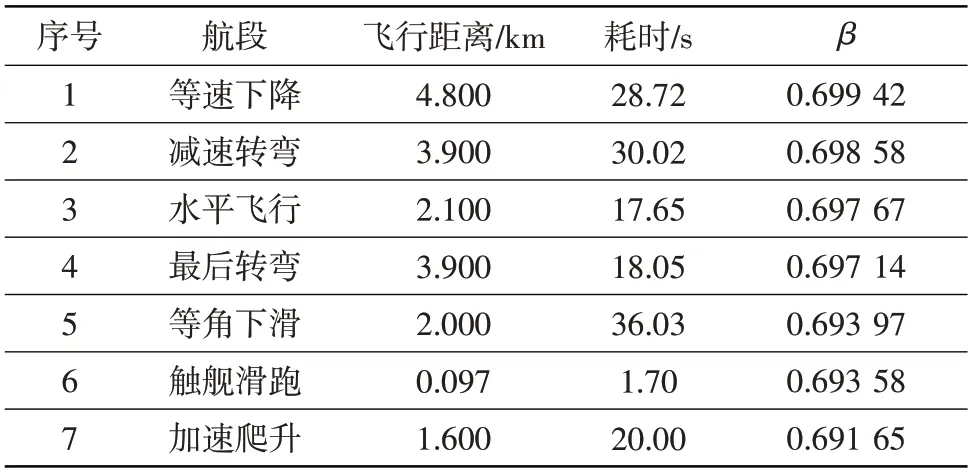
表2 舰载机各个航段计算结果Table 2 Calculation results of each segment process

6.2 舰载机复飞性能分析

根据建立的飞/发一体化控制模型对舰载机进行复飞性能评估。选定确定的着舰β值，在不同甲板风速下计算舰载机起飞速度和甲板长度，结果如图7所示。可看出，随着甲板风速增加，起飞速度减小，所需要的甲板长度也缩短。由于β值一定时，其对应的起飞速度基本不变，所以当甲板风速增加时，起飞速度减小，甲板长度也相应缩短。

图7 β为0.69时起飞速度和甲板长度的对应关系Fig.7 Change of the speed of disembarkation and length of deck with the wind on the deck when β is 0.69

当甲板风速不变(12.86 m/s)时，根据不同的着舰β值计算舰载机的起飞速度和所需甲板长度，结果如图8 所示。可以看出，随着着舰β值增大，舰载机的起飞速度和甲板长度也不断增加。这是因为当舰载机着舰重力增大时，为满足舰载机起飞条件(基本条件为飞行器升力等于重力)，必须增加起飞升力，而起飞升力的增加取决于起飞速度，表现为增加起飞速度来平衡着舰β值的增加，相应的甲板长度也增加。

图8 舰载机的起飞速度和所需甲板长度随β的变化关系Fig.8 Change of the speed of disembarkation and the length of deck slippage with β

舰载机着舰时面临不同的甲板风速，由于风速会对复飞性能产生影响，为了在有限的甲板长度上成功复飞，舰载机必须控制相应的着舰重力。经计算，不同甲板风速对应的最大着舰重力如图9 所示。可看出，当甲板长度一定时，最大着舰重力随着甲板风速增大也相应增加。

图9 甲板长度固定时最大着舰重力和甲板风速的关系Fig.9 The relationship between the maximum weight of landing and deck wind when the length of deck is fixed

7 结论

基于发动机动态模型和舰载机气动模型，以舰载机着舰复飞过程为任务剖面，建立了准确表达舰载机动态特性的飞/发一体化控制模型，并以此模型为基础，开展了舰载机复飞参数变化分析。得到的主要结论为：

(1) 设计了舰载机复飞时发动机的最大状态控制规律，基于飞/发一体化控制模型设计的复飞供油规律为sfcfb=sfcfb,85%+0.628t。

(2) 基于飞/发一体化控制模型，得到了着舰不同航段对应的飞行距离、耗时和β值。各航段所耗燃油量不大，不能通过该阶段直接调节着舰重力，但可通过抛洒燃油等方式调节着舰重力。

(3) 获得了甲板风速、甲板长度、舰载机最大着舰重力三者间的关系。当着舰β值一定时，对应的起飞速度基本不变；当甲板风速增加时，起飞绝对速度减小，起飞甲板长度也相应缩短。