带均压槽双面空气静压止推轴承自激振动的刚体-流场耦合非定常压力脉动分析

李剑雄，侯安平，张久峰

(北京航空航天大学能源与动力工程学院，北京 100191)

1 引言

现代工业应用对于气体静压止推轴承的承载力和刚度等性能要求越来越高，而增加均压槽等提高刚度的措施很容易引起止推轴承气锤失稳[1]，造成转轴剧烈振动，同时伴随着尖锐的气动啸叫，进而导致轴承失效。

针对气体静压止推轴承的气锤稳定性问题，学术界开展了广泛的研究。Powell[2]首次深入探讨了气锤振动现象，指出气锤是一种自激振动，认为气体的可压缩性导致轴承气膜的运动相位改变了180°是引起气锤的主要原因。里见忠笃等[3]研究发现，增大节流孔直径和增设均压槽使得轴承更容易引起气锤现象。Al-Bender[4]提出，简谐振动的形式与轴承振动的形式相一致，可以作为典型扰动形式用于研究气体静压轴承动态特性。李运堂等[5]用大涡模拟分析小孔节流静压气体轴承内气体的流动特性，确定节流器出口湍流区域产生的旋涡破碎是微幅自激的直接原因。翟延武[6]计算并试验验证了气锤自激振动产生与轴承参数的关系，认为共振是引起气锤现象的主要原因。刘暾等[7-11]认为，气锤的产生是因轴承内气体压缩造成的作用力滞后，不断积累能量，出现连续振动导致。郭良斌等[12-13]用能量法对气锤自激进行解释，认为由振荡流动部位形成的非定常力决定了一个周期内振动物体功的稳定性，如果流体不稳定力对振动物体做负功，则流体在振动期间起到阻尼作用，振动衰减，即系统稳定。

本文针对带均压槽的双面空气静压止推轴承发生气锤自激时的振动和流场压力脉动，利用ANSYS CFX进行刚体-流场耦合瞬态模拟仿真，并对计算所得非定常压力脉动现象进行探讨，初步探索了流场压力脉动和轴振动位移之间的相位关系与轴承系统自激振动的相关性。

2 分析模型

2.1 控制方程

采用连续方程、动量方程和能量方程形式的Navier-Stokes方程作为控制方程[14]。

式中：ρ为气体密度；∇为梯度算子；U 为气体速度；p为气体压力；单位气体总焓h*=h+1/2U2，其中单位气体静焓h=cpT，cp为气体定压比热容，T为气体温度；热流密度q=-λeff∇T，其中等效导热系数λeff=λ+λt，导热系数λ=cpμPr，湍流导热系数λt=cpμt/Prt，层流普朗特数Pr设为0.72，湍流普朗特数Prt设为0.90；τ与应变相关，可表示为

式中：δij表示克罗内克函数，等效动力黏度μeff=μ+μt，μ为气体动力黏度，μt为湍流黏度且可表达为

式中：k为湍动能，ε为湍动能耗散率。

k、ε可根据湍动能公式及湍流耗散率公式求得。

式中：cμ、c1、c2、σk、σε为常数。

2.2 计算模型

计算模型采用了应用最为广泛的带均压槽的双面止推轴承，如图1 所示。该轴承的初始设计点参数见表1。

图1 带均压槽的双面止推轴承及其转轴示意图Fig.1 Double-sided aerostatic thrust bearing-rotor system with circumferential equalizing groove

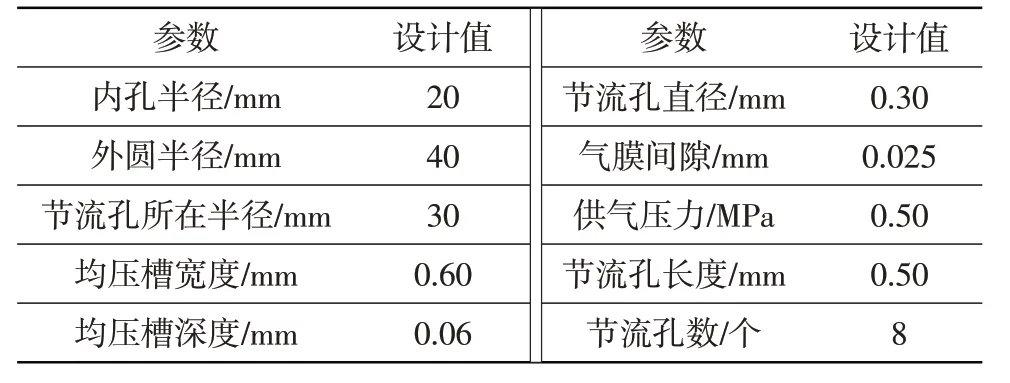
表1 轴承初始设计点参数Table 1 Bearing parameters of initial design

为方便建模，减小止推盘厚度，取轴承与止推盘之间的空气间隙作为计算域，如图2 所示。由于节流孔数量为8 个，可采用1/8 模型进行计算，整体网格数量约160万。以节流孔轴线与轴平面的交点为原点设立坐标系，以轴承半径方向为x方向，节流孔进气的反向为y方向。进口为给定供气压力边界条件；出口为开放边界条件；轴承两侧为周期性边界；计算域的轴双侧，即两个止推面设置为刚体边界条件，进行刚体-流场耦合瞬态计算模拟气锤自激现象，如图3所示。在初始时刻，给定轴承一个微小偏心，轴承因受力不平衡发生位移，在轴承力作用下发生振动。因为气锤振动发生在轴向，因此该刚体设置为允许y方向位移，限制x、z方向和旋转自由度。

图2 计算域和坐标系示意图Fig.2 Computational domain and coordinate system

图3 止推轴面示意Fig.3 Thrust surfaces of shaft

3 结果与讨论

3.1 轴振动和非定常压力脉动频相特征

图4展示了计算得到的轴振动位移和轴承气膜间隙内的非定常压力脉动时域波形。图中轴位移和压力脉动幅值均随着时间增加而逐渐增大，当轴振动位移增大到接近轴承间隙时，轴承与轴发生碰磨，轴承失效。

图4 轴振动位移和压力脉动时域波形Fig.4 Waveforms of shaft displacement and pressure fluctuation

将轴振动位移和压力脉动时域波形进行傅立叶变换，得到轴振动位移和气膜间隙内压力脉动的频域波形，见图5。对计算域内多点的压力幅值做平均值平移后进行频谱分析，占优频率均为177.5 Hz，与轴振动频率相等，说明流场中的压力脉动频率都等于轴的振动位移频率。

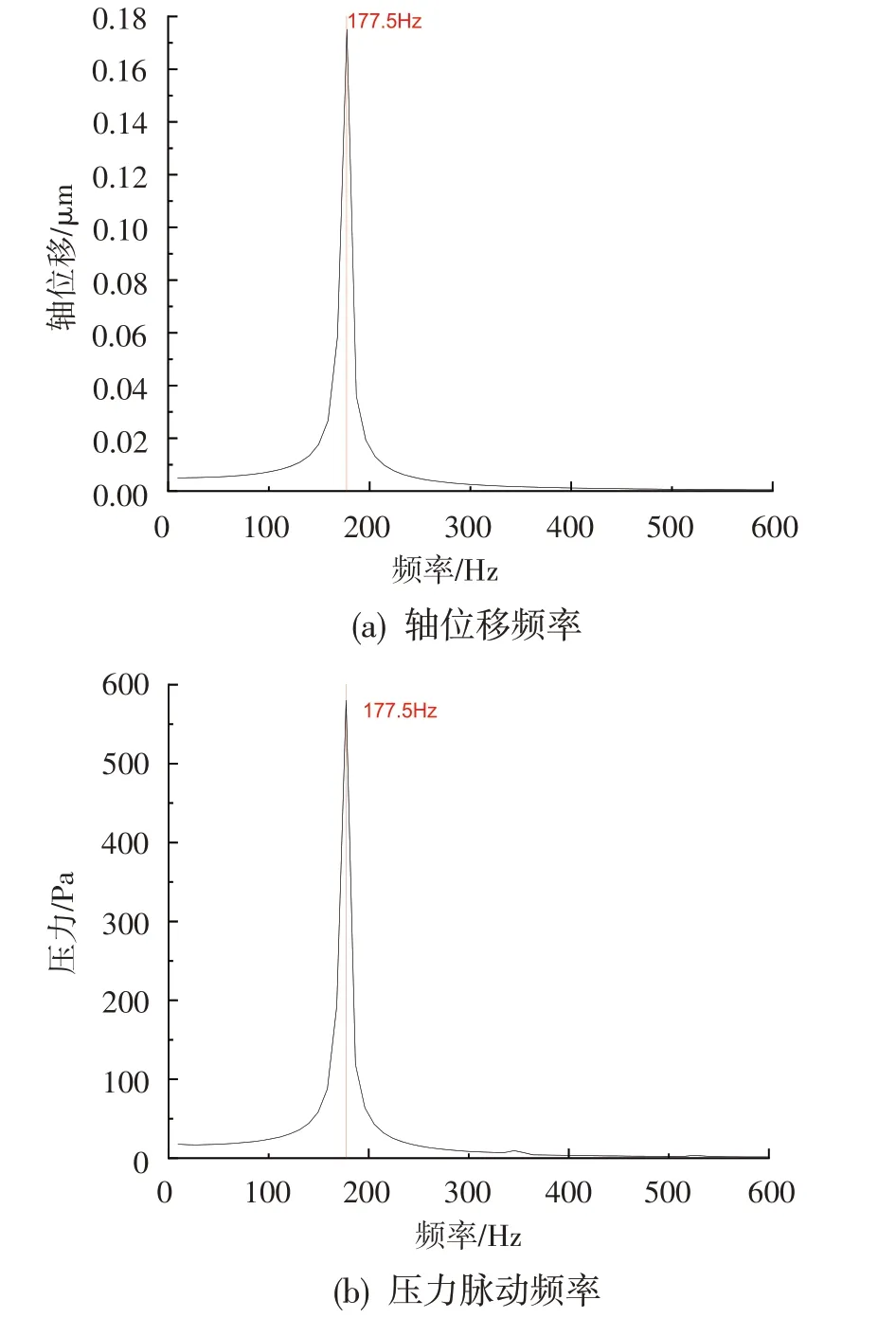
图5 轴位移频率和压力脉动频率Fig.5 Frequency domains of shaft displacement and pressure fluctuation

以轴的振动相位为参考，可以得到轴承气膜流场内任意位置压力脉动与轴振动位移之间的相位差，分别在xz和xy平面内将相位差相等的点连接起来，即可得到xz和xy平面的等相位差图，如图6 所示。分析可知，在平行于轴承面的xz平面内，原点处相位差最大，该点即气流从节流孔流出喷射到止推面的速度滞止点；随着该气流向四周扩散，相位差沿半径方向逐渐减小，并在距离原点150 μm处降低到接近0°。而在垂直于轴承面的xy平面内，沿高度增加方向，越贴近止推面相位差越大，且随着高度增加相位差快速降低。通过xz与xy平面的等相位差图分析得知，气膜厚度方向相位差降低速度比半径方向的降低得更快。xz平面内，等相位差线为椭圆，即z方向的相位差变化得比x方向的慢，相位差扩散范围更大。

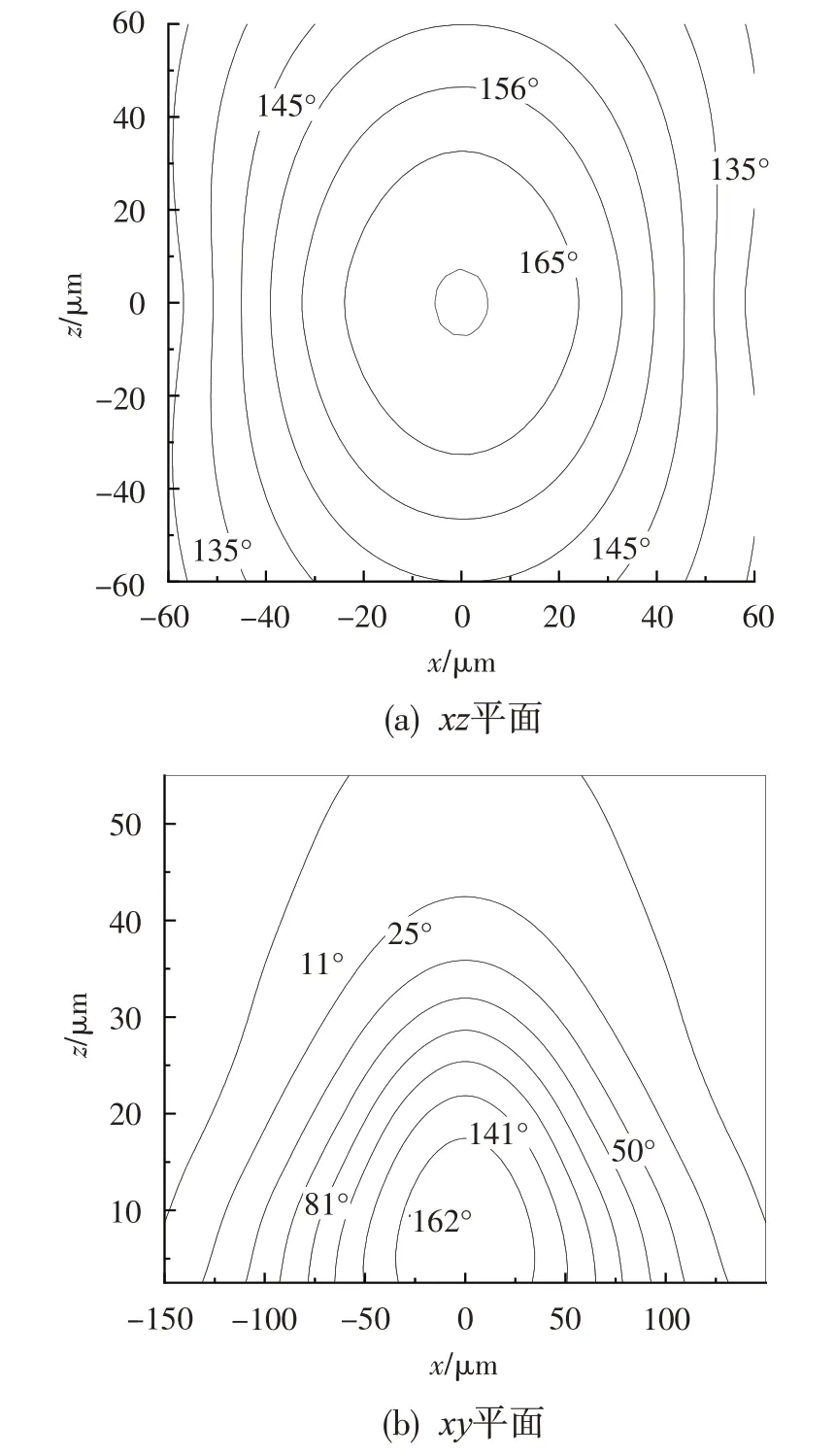
图6 xz平面和xy平面的等相位差图Fig.6 Equal phase difference diagrams in xz and xy plane

图7示出了x分别为0，-30，-60 μm位置，沿y方向从2.5 μm 到55.0 μm 不同高度位置的相位差变化。图8示出了最靠近止推面的y=2.5 μm平面相位差分布。可直观地看到，x方向和y方向上相位差的变化趋势相似，随着距离增加相位差逐渐减小，且变化速度先增大后减小，相位差为0°的点即为滞止区域的边界。

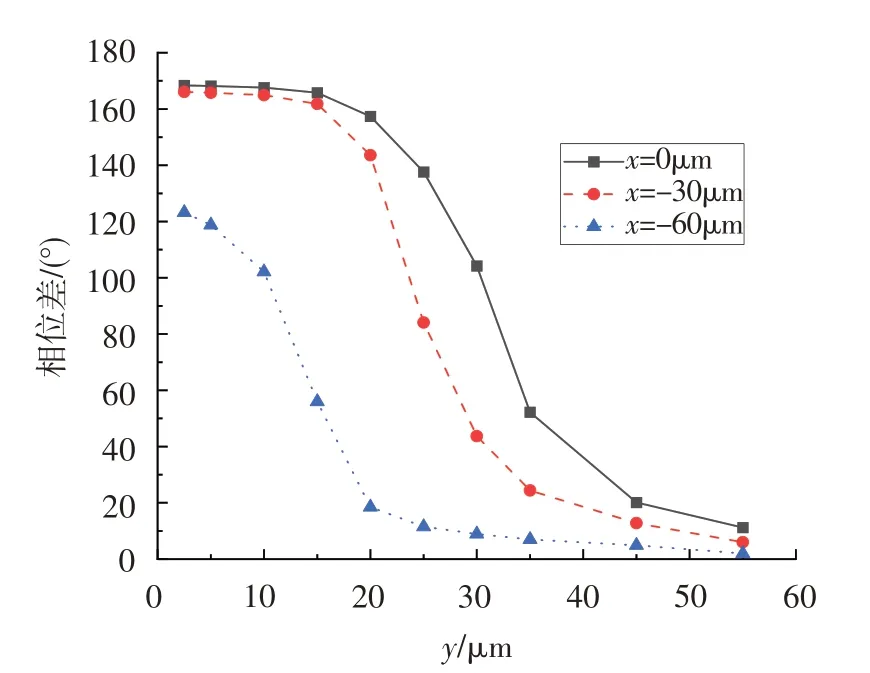
图7 y方向相位差分布Fig.7 Phase difference distribution inydirection

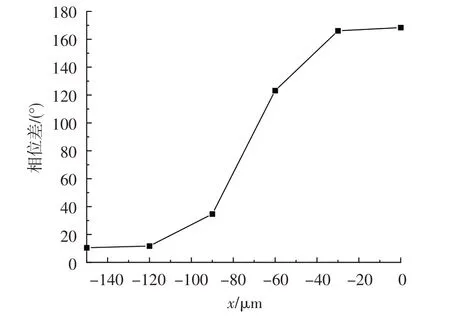
图8 y=2.5 μm平面x方向相位差分布Fig.8 Phase difference distribution in x direction when y=2.5 μm

3.2 非常定流场局部细节分析

图9、图10 分别展示了yz平面和xy平面内的马赫数和压力云图以及流线图。可清晰地看到，由于均压槽的存在，导致x方向与z方向的气流运动存在明显差异。

图10 xy平面马赫数和压力云图以及流线图Fig.10 Mach number,pressure and streamline contours on xy plane

气流从节流孔进入轴承间隙的整个过程可分为三个阶段。第一阶段，高压气流垂直于止推面从节流孔进入轴承，冲刷到止推面上，气流速度滞止为0。该阶段，气流从初始速度急剧减小到0，在原点附近制造了一个近似半椭球形的低速区，该低速区占据了大部分的节流孔面积，导致气流的有效通道面积大幅度减少，产生了一个气流通道喉部。第二阶段，滞止的气流制造了一个局部高压区，导致气体以近90°的角度转向均压槽扩散流动。该阶段气流剧烈转向，高速气流区获得了更大的通道，并且持续增大，同时在均压槽的角区形成涡流。在第一和第二阶段中，气流通道先减小后增大，形成了类似拉瓦尔喷管的收敛-扩张流道，将气流加速到超声速状态。第三阶段，气流在均压槽中发展后，通过均压槽和间隙的连接部分进入小尺度的轴承间隙。该阶段x方向上，受均压槽宽度限制，气流迅速进入轴承间隙内，流动通道减小，流动进入亚声速状态；而气流进入间隙后，由于呈圆形扩散，通道面积再次增加，气流再次加速到超声速，并迅速被小间隙限制为层流状态。y方向气流一直在均压槽内流动，流动充分发展，滞止区范围比x方向的更大。

3.3 不同参数时的轴承稳定性与相位差分析

保持轴承设计点其他参数不变，只改变供气压力(分别为0.45 MPa 和0.60 MPa)，得到如图11 所示的轴位移时域波形。可看到，供气压力为0.45 MPa时，止推轴承的轴振动时域曲线最终收敛，即没有发生气锤自激现象，系统稳定；供气压力为0.60 MPa时，轴振动时域曲线振幅随时间逐渐增大，轴系统能量持续增加直至发散，即会发生气锤自激现象，系统失稳。

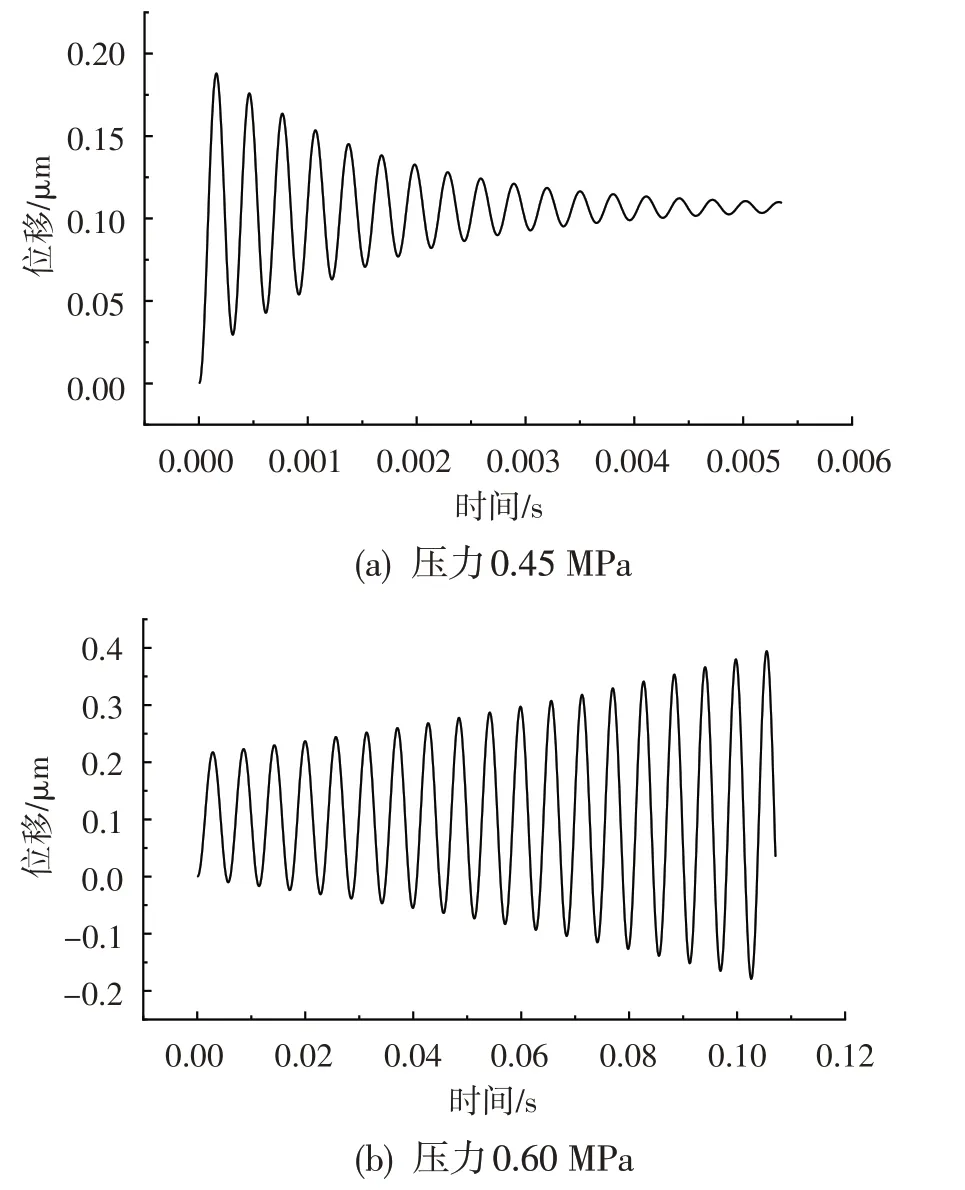
图11 供气压力分别为0.45 MPa和0.60 MPa时的轴振动位移曲线Fig.11 Waveforms of shaft displacement when supply pressure is 0.45 MPa and 0.60 MPa alternatively

图12为不同供气压力下，高度分别为2.5 μm和15.0 μm 平面内，z=0 的各点位置的相位差。可看到，当压力增大时，存在相位差的范围明显增大，即滞止区域面积增加。

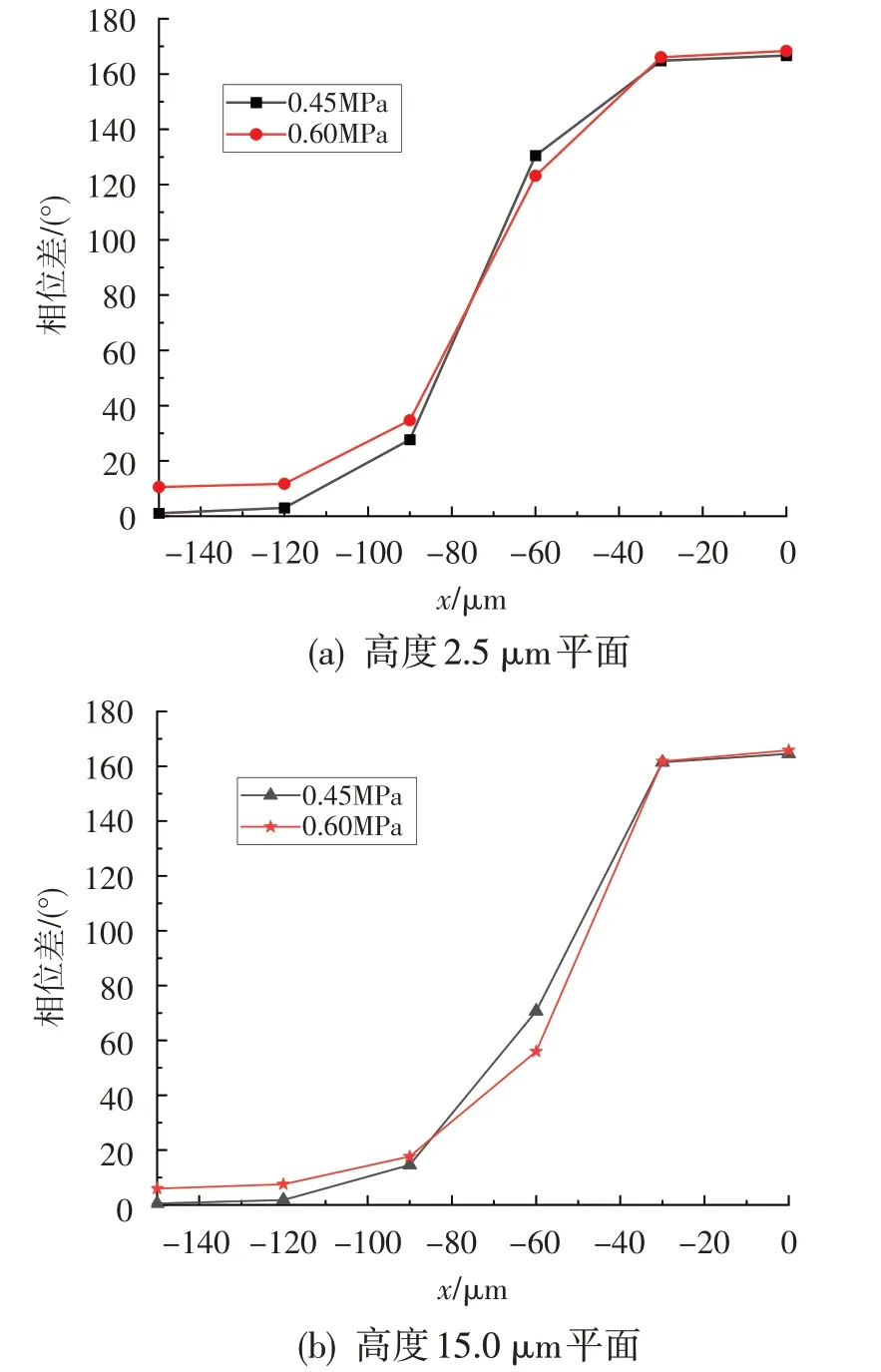
图12 两种供气压力下不同高度平面内的相位差对比Fig.12 Phase difference comparison of two pressures in different planes

保持轴承设计点其他参数不变，只改变槽深(分别为0.045 mm 和0.060 mm)，得到如图13 所示的轴位移时域波形。当槽深为0.045 mm时，止推轴承的轴振动时域曲线呈现收敛现象，即不会发生气锤自激现象，系统稳定；当槽深为0.060 mm时，轴振动时域曲线振幅逐渐增大，系统能量增加且一直持续，即会发生气锤自激现象，系统失稳。

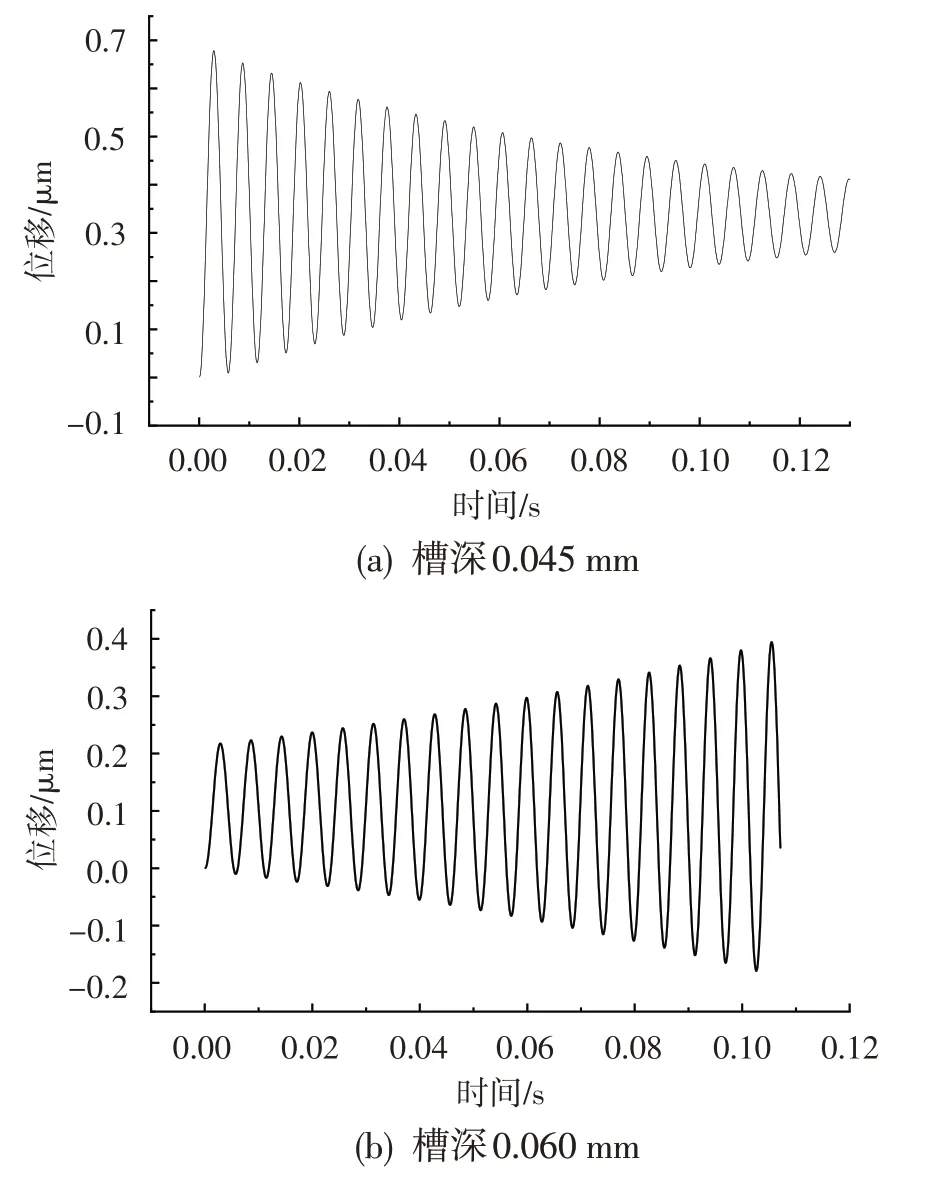
图13 槽深0.045 mm和0.060 mm时的轴振动波形Fig.13 Waveforms of shaft displacement when groove depth is 0.045 mm and 0.060 mm alternatively

图14为不同均压槽深度下，高度分别为2.5 μm和15.0 μm平面内，z=0的各点位置的相位差。可看到，当均压槽深度增加时，存在相位差的范围明显增大，即滞止区域面积增加。

图14 两种槽深下不同高度平面内的相位差对比Fig.14 Phase difference comparison of two groove depth in different planes

4 结论

(1) 静压止推轴承转轴系统中，轴承气膜间隙内压力脉动频率处处相等，且等于轴振动位移频率。

(2) 轴承节流孔与均压槽的交汇处，流场内的压力脉动与轴振动存在相位差，相位差在气流从节流孔进入轴承后的速度滞止点最大，接近180°，并且以该点为中心向外减小。

(3) 轴承气膜流场压力脉动与轴振动的相位差在轴承气膜厚度方向迅速减小到0°；在气流流向平面内，均压槽限制了相位差的分布范围。

(4) 增大轴承供气压力或均压槽深度导致气锤自激现象时，轴承气膜流场压力脉动与轴振动的相位差的分布范围明显扩大。