基于深度学习的结构可靠性分析方法研究
2022-01-17李明刚聂常华刘志龙
欧 柱,李明刚,聂常华,刘 杰,刘志龙,罗 骞
(中国核动力研究设计院, 成都 610213)
0 引言
结构可靠性作为产品的重要属性之一,越来越受到机械行业的重视。近年来,我国相继启动一系列重大工程,如载人空间站、大飞机项目、先进轨道交通、深海探测载人潜水器、航空母舰等。这些重大工程中的服役产品普遍存在缺乏统计数据,使用环境恶劣等问题,对可靠性评估提出了更为严苛的要求。因此,必须在产品分析与设计环节采用更为高效的可靠性分析理论对运行可靠性进行有效评估,否则一旦发生故障,将造成巨大的经济损失和人员伤亡。
针对机械结构可靠性评估,国内外学者提出了很多计算失效概率的方法,如一次二阶矩法[1]、重要抽样法[2]、子集模拟法[3]、方向采样法[4]、响应面法[5]和蒙特卡洛(Monte Carlo,MC)法[6-7]等。这些方法为结构可靠性理论的发展作出了巨大贡献。在结构可靠性评估中,MC法由于其简洁易懂、适应性强、普适性好而被广泛使用,而且常常被视为基准算法用来验证其他方法的计算精度。MC法最大的不足在于计算失效概率时的高计算成本问题,特别是对于非常耗时的有限元计算或其他仿真。因此,对于工程应用,直接采用MC法计算失效概率会面临巨大的挑战。
国内外大量学者为降低MC法自身不足所带来的影响,常将MC法和其他数学理论进行结合。该方式既确保了MC法的强适应性,又弥补了其自身的不足。其中使用较多的当属各类代理模型,如Kriging模型[8]、人工神经网络模型[9]、支持向量机(support vector machine,SVM)模型[10]以及混沌多项式模型[11]等。上述代理模型中涉及的人工神经网络模型仅为浅层次学习模型,属于经典机器学习理论的范畴。2006年,Hinton等[12]首次提出的深度学习理论成为了近年来处理数据的一把利刃。深度学习是通过模拟大脑的学习过程,构造深层次模型,并结合海量数据进行学习,从而刻画数据的有效特征,最终提升分类或预测的精度。相对经典机器学习理论,深度学习理论不需要人为提取特征,而是机器自主学习,因此可进行更深层次学习,找到全局最优解。深度信念网络(deep belief network,DBN)作为深度学习的一种代表性方法,可以通过组合低层特征形成更加抽象的高层表示,从而发现数据的分布特征。它从低层原信号出发,逐层贪婪学习获得高层特征的学习网络,排除了人为影响。目前,DBN被广泛运用到故障诊断[13-14]、图像识别[15]和语音识别[16]等方面,但在结构可靠性评估中应用得较少。鉴于此,本文将DBN模型引入到结构可靠性评估中,详细阐述了整个评估计算流程,并代入算例,验证方法的可行性。
1 深度信念网络
本节首先对DBN物理模型结构进行介绍,接着对DBN参数结构进行介绍,最后对DBN参数结构优化进行介绍。DBN物理模型结构主要为受限制玻尔兹曼机(restricted Boltzmann machine,RBM)的堆叠过程。DBN预训练是RBM逐层贪婪训练过程。本文给出单个RBM参数训练过程,其余堆叠的RBM通过类推可得。DBN参数优化过程是每个RBM参数优化过程的堆叠。本文给出最后一个RBM参数调优过程,其余RBM优化过程从最后一个类推到第一个即可得到。
1.1 DBN物理模型
对多个RBM进行堆叠,将前一层的输出作为后一层的输入,这样就构成了DBN模型。RBM模型和对应DBN模型如图1所示。图1中,每个低层RBM对输入数据进行训练并输出到高层RBM作为输入,逐层传递形成完整的DBN结构,在最高层形成更抽象、更具有表征能力的特征向量。与反向传播(back propagation,BP)神经网络相比,DBN的一大优势是将训练得到的权值用于初始化其他相同结构的网络参数,以此避免因随机初始化参数而陷入局部最优和训练时间过长的困境。

图1 RBM模型和对应DBN模型Fig.1 RBM model and corresponding DBN model
对一个完整的DBN模型,其训练过程分为以下两步。
①预训练阶段采用无监督逐层贪婪训练的方法,从底层到高层,逐次训练每层RBM的参数,确保低层特征向量映射到高层特征空间时,尽可能多地保留特征信息。
②经过预训练后,将整个深度网络视为传统的BP神经网络,进入有监督微调的阶段,即从网络的高层到低层,根据误差的传播,依次对每层的参数进行微调,以修正整个DBN的权值。
对训练好的DBN模型进行分类,只需要在模型的尾部加一个分类器即可。目前,使用比较多的分类器有softmax和SVM两种。
1.2 DBN预训练
DBN的预训练是RBM的逐层贪婪训练。因此,本部分仅给出了单个RBM的预训练。RBM是一种神经感知器,由一个显层和一个隐层构成。显层与隐层的神经元之间为双向全连接。RBM网络结构如图2所示。
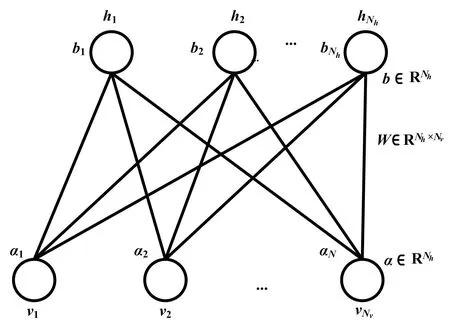
图2 RBM网络结构示意图Fig.2 RBM network structure diagram
图2中:v=[v1v2…vNv]为显层节点;h=[h1h2…hNh]为隐层节点;W={wij},1≤i≤Nh,1≤j≤Nv为显层节点和隐层节点之间的连接权重;a=[a1a2…aNv]和b=[b1b2…bNh]分别为显层节点和隐层节点的偏置向量。
RBM的优点是所有显层(隐层)节点独立于其他显层(隐层)节点,因此可以通过使用基于层的快速学习算法来训练网络,例如对比散度方法。
对于一个给定状态(v,h)的RBM,可定义其能量函数为:
(1)
式中:θ为RBM中的参数,θ=(W,a,b)。
状态(v,h)下的联合概率分布可以根据吉布斯分布得到:
(2)

由式(2)可得显层和隐层的边缘分布为:
(3)
(4)
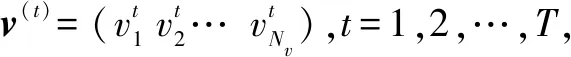
(5)
为方便求偏导数,式(5)可以改写为:
(6)
通常,参数θ是通过最大化训练集上的对数似然函数学习得到的。
(7)

(8)
式中:η为学习参数,η>0。
1.3 DBN微调
DBN预训练主要用于提取数据特征,并得到一个大范围的优化解集,即预训练并不能得到高精度的最优解,此时就需要启用反向微调算法。DBN反向微调和BP神经网络反向调节方法相同。具体过程如下所述。
网络的最后一层由Softmax作为分类器,DBN微调也是从最后一层逐层向前进行的。现假设DBN由l个RBM模型堆叠而成,另有若干个训练样本表示为S={v(1),v(2),…,v(T)},v(i)=(x1x2…xm),i=1,2,…,T,T为m维的样本向量。则最后一层输出向量为:
(9)
第i个样本经前向l层堆叠RBM学习后,属于类别yi(yi∈[1,2,…,c])的概率为:
(10)
式中:V为参数系数,选取最大概率所对应的类别即为Softmax模型判别类型。
第l层误差函数表达式为:
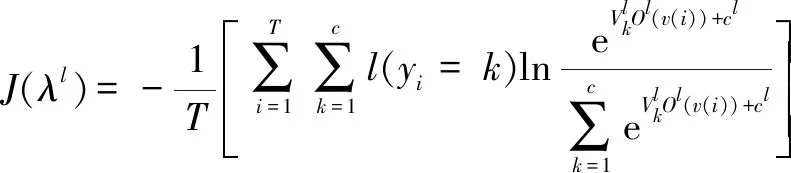
(11)
式中:λl为第l层的参数集合,λl={wl,bl,cl,Vl};l(yi=k)为逻辑指示函数,当yi=k时值为1,当yi≠k时值为0。
为求误差最小值,使用梯度上升法,对参数求偏导如下:
(12)
最终进行微调,参数如式(13)所示:
λl=λl-αλlJ(λl)
(13)
式中:α为学习率。
以此类推,可以微调1层到l层相关参数。
2 基于DBN的可靠性分析方法
2.1 MC法
在结构可靠性分析当中,通过对随机变量的联合概率密度函数进行积分,可以得到失效概率的准确值。失效概率的具体积分过程可如式(14)所示:
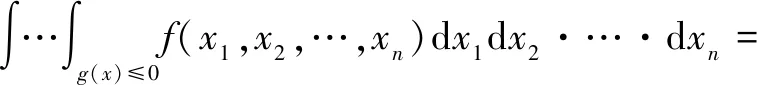
E[IF(x)]
(14)
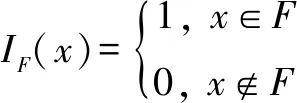
但是在复杂的可靠性分析中,因为概率密度函数极难获取,所以通常计算失效概率采用的是MC法而不是积分的方法,可以表示为:
(15)
式中:xj为由伪随机发生器根据联合概率密度函数生成的第j个伪随机样本点;N为总样本点数;Nf为失效样本点数。
2.2 基于深度信念网络的结构可靠性评估法

得到训练模型以后,根据随机变量的联合概率密度函数f(x;μ,σ2)生成N个需要的数据样本xj(j=1,2,…,N)。将xj(j=1,2,…,N)代入训练好的模型并且判断该样本是否为失效样本,并计算失效概率。基于DBN的失效概率估算流程如图3所示。该流程具体步骤如下。
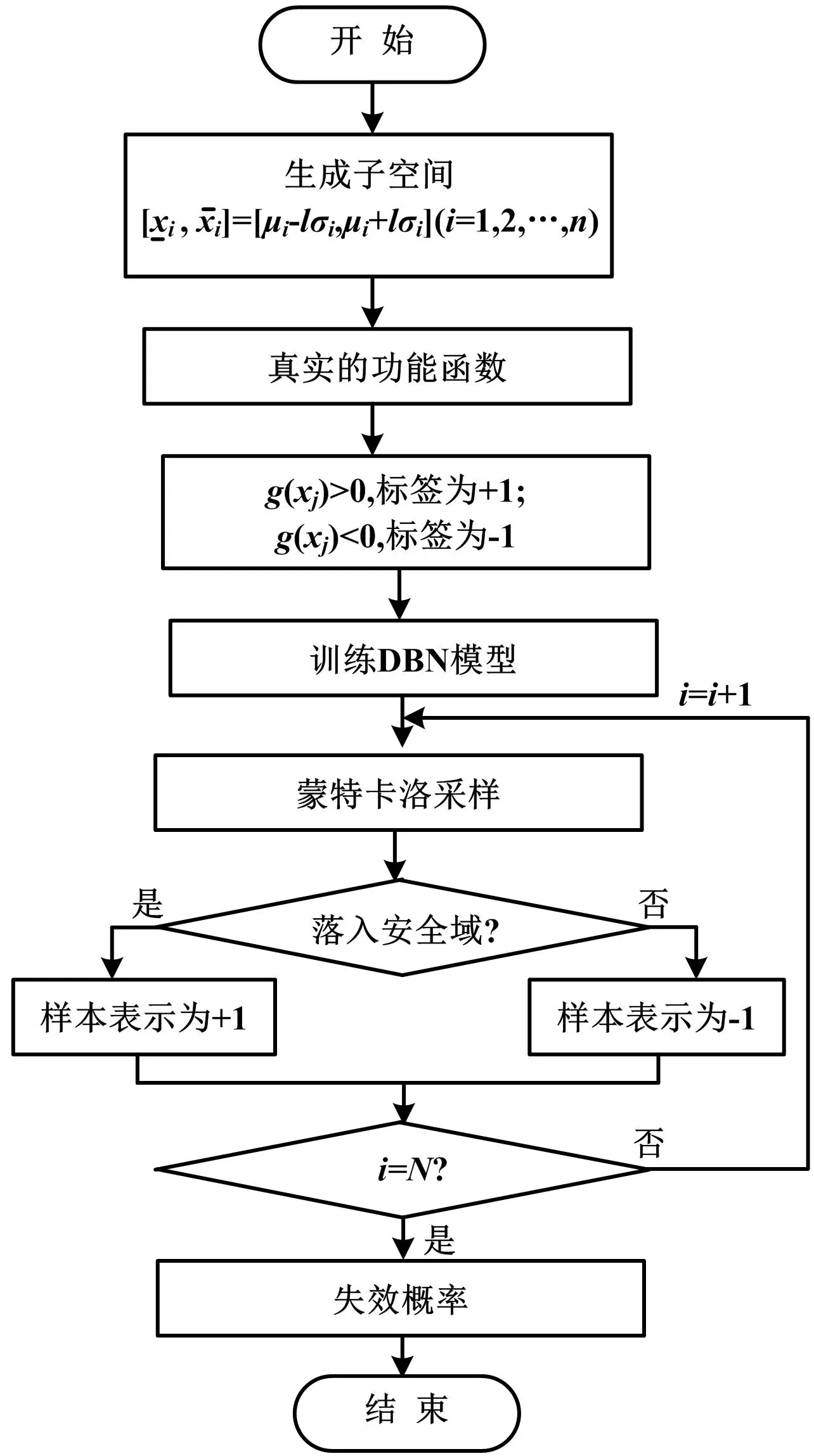
图3 基于DBN的失效概率估算流程Fig.3 Estimation process of failure probability based on DBN
②通过极限状态函数,可以求出Ntraining个训练样本中的失效样本和安全样本。
③根据训练样本训练DBN模型,包括DBN的预训练和微调两部分。
④根据联合分布概率密度函数f(x;μ,σ2),使用伪随机数发生器生成N个样本xj(j=1,2,…,N)。利用训练好的DBN模型代替功能函数判断第j个训练样本xj(j=1,2,…,N)是否落入安全域。如果它落入安全域,则对应的样本点标签为+1,然后判断下一个样本点;如果它落入失效域,则对应的样本点标签为-1。

(16)
(17)
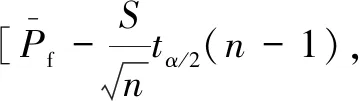
(18)

3 算例
为了说明本文所提出算法的精度和效率,将给出一个数字算例和一个工程算例。数字算例主要是为了说明该方法的精度,而工程算例则主要是为了说明该方法的效率。
3.1 数字算例
算例1 现有一个非线性功能函数如下所示:
g(x)=2x1x2x3x4-x5x6x7x8+x9x10x11x12
(19)
式中:xi为服从均值为8、方差为1的正态分布的变量,即xi~N(8,1)(i=1,…,12)。
对于式(21)中的功能函数,分别使用MC法和建立的DBN模型来求解失效概率、失效概率的标准差,并在此基础上求得了DBN模型相对于MC法的相对误差。算例1计算结果如表1所示。

表1 算例1计算结果Tab.1 Calculation results of Example 1
表1中,MC法作为一种标准来验证本文提出的模型,平均失效概率为100次失效概率的平均值,每次进行106次抽样。DBN每次的训练样本个数为4 000。由表1结果可知,两种方法所计算的平均失效概率值很接近,相对误差不到2%。因此,DBN模型可以运用在结构可靠性分析中。
算例2 现有一个具有两个极限状态函数的并行系统y=g(x)=max{g1(x),g2(x)}。其中,两个函数为y1=g1(x)和y2=g2(x),可以被重新定义为:
(20)
式中:c=4,xi为相互独立的标准正态分布变量,即xi~N(0,1),i=1,2。
针对式(22),分别利用MC法和DBN模型去求解失效概率。算例2计算结果如表2所示。
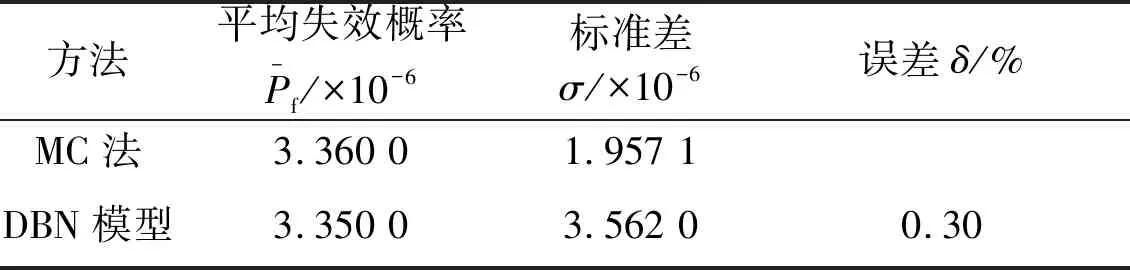
表2 算例2计算结果Tab.2 Calculation results of Example 2
表2中的DBN模型利用4 000个训练样本点,采用DBN方法进行训练。其中,平均失效概率为100次失效概率的平均值,每次进行106次抽样。从表2可以看出,DBN模型与MC法计算出的失效概率非常接近,分别为3.36×10-6和3.35×10-6,相对误差为0.3%。因此,本文所提出的DBN模型在一定程度上可以替代传统的MC法。
3.2 工程算例
本实例考虑单摆振荡问题,并且对摆动的最大振荡角速度进行研究。最大振荡角速度不能低于y0=309 rad/s,否则认为钢棒失效,则相应的功能函数可以表示为:
y=g(r,L,ρ)-y0
(21)
式中:r、L和ρ分别为钢棒的半径(m)、长度(m)以及密度(kg/m3)。这三个变量之间相互独立,且服从正态分布,均值分别是μr=0.01、μL=1及μρ=7 930,标准差为σr=10-4、σL=0.007及σρ=0.05。

该算例使用Simulink建立单摆的振荡模型,其Simulink仿真模型如图4所示。分别使用MC法和DBN模型对失效概率进行估计,仿真计算结果如表3所示。由于仿真中利用MC法进行失效概率所花费的时间太长,本算例以105次仿真为例进行说明。
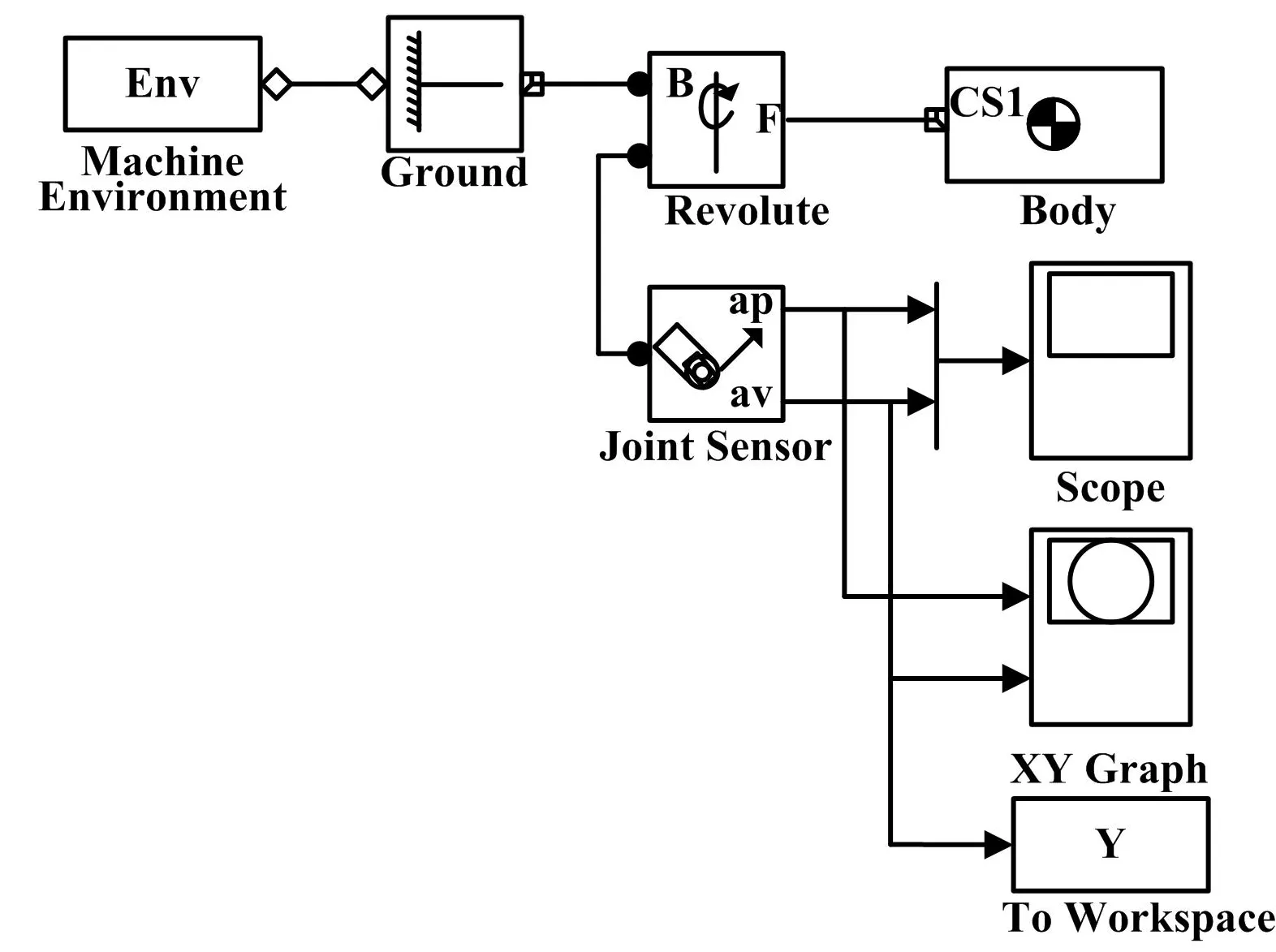
图4 Simulink仿真模型Fig.4 Simulink simulation model
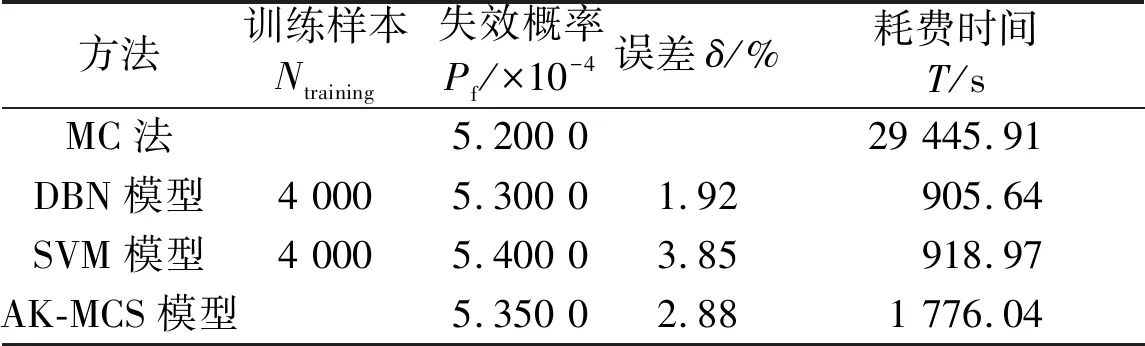
表3 仿真计算结果Tab.3 Simulation results
从表3可以看出,以MC法为参考时,DBN模型计算的失效概率与MC法计算的失效概率之间相对误差仅为1.92%,但是MC法所消耗的计算时间却约为DBN模型的32倍。这是因为MC法耗费了100 000次仿真时间,而DBN只耗费4 000次仿真时间。为了进一步对比该方法的准确率和效率,分别运用SVM模型和克里金-蒙特卡洛结合仿真(active Kriging and Monte Carlo simulation,AK-MCS)模型进行对比,可知DBN模型的精度最高,证明所提出的模型极大地提高了问题分析效率。
4 结论
本文提出的方法在数字算例中对精度和传统的MC法进行对比,结果表明提出的DBN模型有较高的计算精度。
在工程算例中对DBN模型的效率进行了对比,结果表明提出的DBN模型能够将传统的计算方法效率提高约32倍,和传统的可靠性评估方法(SVM模型和AK-MCS模型)进行对比,结果表明所提出的DBN模型精度最高。
