聚焦三角函数问题中的常用数学思想

■冉淑华

三角函数是高中数学的重要内容之一,其中蕴含着丰富的分类讨论思想、等价转化思想、函数与方程思想、换元思想、整体代换思想等。下面举例说明,供大家学习与提高。

一、分类讨论思想

分类讨论思想的基本思路是将一个较复杂的数学问题,分解(或分割)成若干个基础性问题,通过对基础性问题的解答来实现解决原问题的思想策略。

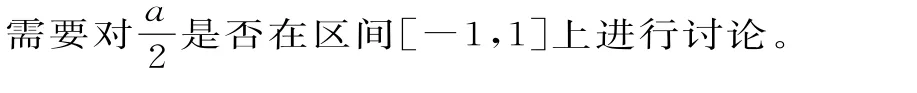
二、对称思想

对称思想是研究数学问题常用的思想方法,对称是一种美。数学中的对称美主要表现在几何图形的对称、式子的对称、解题方法的对称等方面。

三、等价转化思想

解决数学问题,离不开转化与化归思想,如未知向已知的转化、新知识向旧知识的转化、复杂问题向简单问题的转化、不同数学问题之间的互相转化、实际问题向数学问题的转化等。

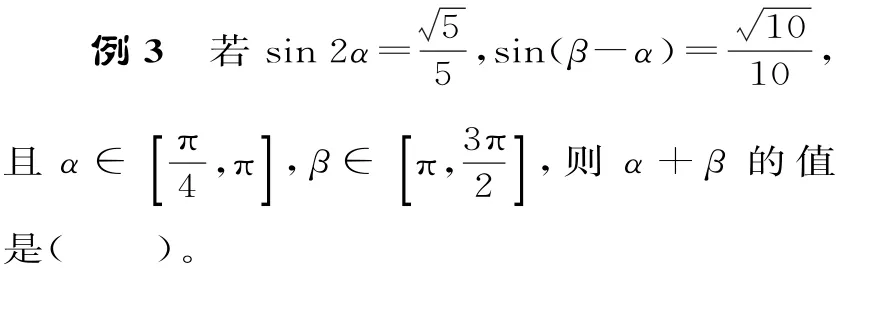
四、换元思想

解题时,把某个式子看成一个整体,用一个变量去代换它,从而使问题得到简化,这叫换元法。换元法的实质是转化思想的应用。

评析:在三角恒等变换中,有时可把一个代数式整体视为一个“元”来参与计算和推理,这个“元”可以明确地设出来,但要注意新元的取值范围。

五、方程思想

方程思想就是利用变量间的等量关系,建立方程或方程组,通过解方程或方程组,或者运用方程的性质去分析、转化问题,使问题获得解决。

六、整体代换思想

当已知的代数式中不能求出每个字母的值或求出的值比较烦琐时,往往通过对比已知条件和所求问题之间的联系,考虑在所求问题中把已知条件(或其变式)整体代入,从而使计算变得简洁。整体代换是换元思想的延伸。

例6 已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(2020)=1,则f(2021)的值为( )。

A.-1 B.1 C.3 D.-3

解:因为f(2020)=asin(2020π+α)+bcos(2020π+β)=asinα+bcosβ=1,所以f(2021)=asin(2021π+α)+bcos(2021π+β)=asin(π+α)+bcos(π+β)=-asinαbcosβ= - (asinα+bcosβ)= -1,即f(2021)=-1。应选A。

评析:题中字母较多,不可能求出每个字母的值。利用f(2020)=1,得到asinα+bcosβ=1,从而可得f(2021)的值,这是整体代换思想的具体应用。