浅析诱导公式的导向功能

■刘长柏

学习诱导公式要紧紧抓住“导”,那么诱导公式主要“导”什么呢? 让我们一起来通过例题导出诱导公式的“精彩”。

一、导“角”

诱导公式有一个很重要的功能就是求三角函数值,在求值时有一个原则,即“负角变正角、大角变小角、小角变锐角”,这就是诱导公式的导角功能。

知角求值时,要分析“特殊角”和“待求角”之间的联系,设法用“特殊角”通过诱导公式表示“待求角”。本题的两种解法,看似没有区别,其实是诱导公式的正向与逆向的运用。

二、导“值”

已知一个三角函数的值,求另一个三角函数的值,往往要先利用诱导公式“导”出某一三角函数的值,然后利用同角三角函数的基本关系进行求解。

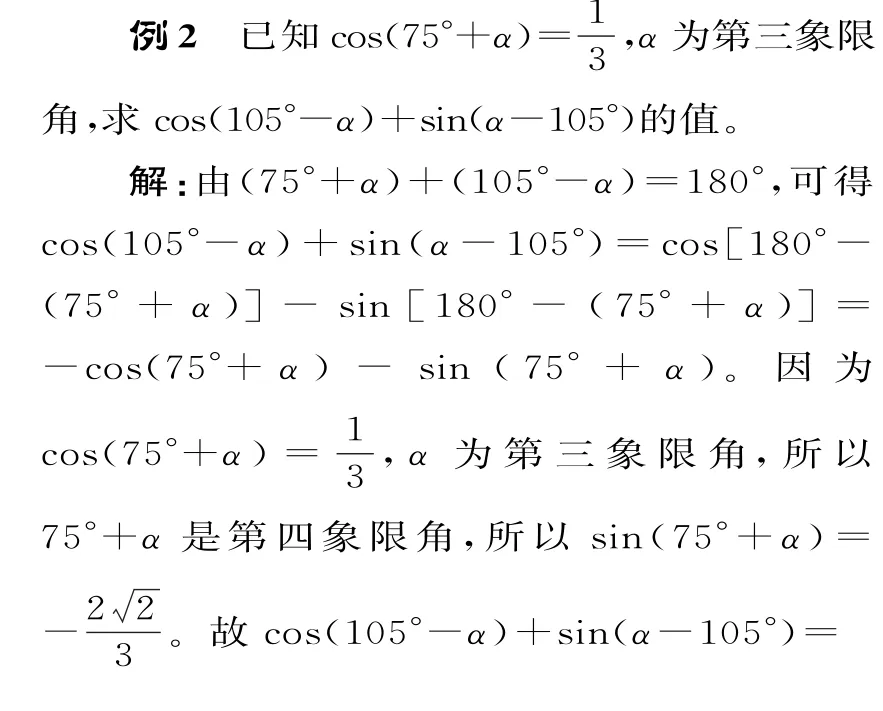
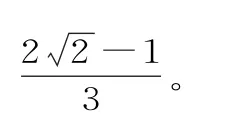
观察角的结构特征,将所求的三角函数值中的角,转化为所给角与特殊角的和与差的形式,实现由未知向已知的转化。

三、导“名”

当函数名称不同时,可以仔细观察角的关系,借助于诱导公式将其“导”为同名三角函数。

例3 求sin21°+sin22°+sin23°+…+sin289°的值。

对于正弦函数与余弦函数的互余关系问题,都可用诱导公式导出所需要的函数,即若α与β是互余角,则sinα=cosβ,cosα=sinβ。