面向狭小空间的起落架收放轨迹智能设计方法

朱林昊，邹泽铧，印寅，刘相阳，蔡新之

（1.南京航空航天大学理学院，南京 210016； 2.南京航空航天大学机电学院，南京 210016；3.南京航空航天大学机械结构力学及控制国家重点实验室，南京 210016； 4.南京工业大学2011学院，南京 211816）

起落装置是飞机实现安全可靠起飞和着陆的重要装置，早期飞机采用不收放的构架式起落架，其结构形式简单，但会产生较大的阻力，因而仅适用于速度较慢的飞机［1-2］。随着飞机速度的不断提升，起落架产生的空气阻力已经影响了飞机的机动性能，因此现代飞机起落架大多采用可收放形式。对于常规飞机而言，舱段空间大多比较充裕，因而起落架收放路径和形式相对简单，如客机B737、A320，其前起落架收入机身前段舱内，主起落架收入机翼中央盒段中，这种方式既不影响飞机的气动外形，也大幅降低了空气阻力［3］。而对于一些空间有限的飞机，起落架难以布置在机身内部，则会在机身外侧增加鼓包来收藏起落架，如US-1、运20、AG-600，但这样的形式会影响飞机的气动外形［4］。

当前，具有重大战略意义的高超声速飞行器飞速发展［5-7］，而可重复使用的定位要求使得高超声速飞行器的研究带来了诸多难题，苛刻的起落架收放空间就是瓶颈问题之一。显然，扁平化的气动外形及大量的燃油储备严重压缩了起落架的收藏空间，而大起降载荷增加了起落架的设计尺寸，这样的矛盾只能限制起落架在合理的运动轨迹下收入狭小的机身舱内，其运动轨迹区别于常规的直前或展向收放形式，大多为空间轨迹线。如何设计空间轨迹线及收放形式则成为起落架设计的一大难题。

传统的方法［8］主要通过理论计算［9］、经验改型和作图法进行设计［10］，这2种思路均采用“设计—制造—试验—改进—设计”的串行设计过程，设计中往往基于经验或根据解析式得到初步的设计［11］，并通过样机试验，进行迭代设计［12-13］。但经验改型和作图法容易造成设计不合理，致使设计反复。理论计算方法对于简单的模型尚可以适用［14］，但是对于复杂的模型而言，计算量巨大，且很难清楚描述几何形态，无法找出起落架收放轨迹的最优解［15］。

随着计算机辅助设计和数字样机技术的快速发展，计算机能够通过CAD和CAE技术［16］，描述起落架的几何外形，通过仿真计算检查起落架运动过程中的干涉问题［17-18］，采用多学科协同仿真技术进行复杂机构的设计、机构运动分析，完成相应的虚拟试验，能够在设计阶段就考虑较多的不确定因素，充分评估各个系统的性能，降低了研制成本并缩短研制周期［19-21］，减少所需实验的次数和复杂性。南京航空航天大学印寅等［22-23］通过仿真软件建立了前起落架的收放动力学模型，分别分析了收放作动器对起落架收放载荷的影响和起落架在收起过程中的动力学性能。虽然相较于传统设计方法，通过计算机辅助技术的发展，可以大幅节省用于作图和进行理论计算的成本，但其采用串行设计模式，仍无法免去人工参与的反复迭代设计。与此同时，由于几何形态的不规则性，该方法得到最优轨迹仍是困难的。

为解决传统设计方法在开展复杂收放机构设计方面存在的局限性问题，本文创新性地提出了基于人工智能自主化设计起落架收放路径的方法。该方法关键在于建立起落架运动模型，处理起落架与机舱环境几何体之间的关系，进行两者的碰撞检测，并选取合适的优化方法进行优化设计。对于碰撞检测而言，主流的三维运动碰撞检测算法按照检测方式分为离散的静态碰撞检测与连续的碰撞检测。前者通过将运动对象的运动划分为多个离散时刻，并对每个时刻进行静态检测，从而完成整体的碰撞检测；后者则通过计算整个运动过程中所形成的四维空间超体进行碰撞检测。相较于前者，连续碰撞检测虽然具有精度高等优点，但运算过程开销较大，故本文使用了离散的静态碰撞检测。面对复杂的优化设计问题，需要选取合适的优化方法。随着近年来人工智能的发展，相应的梯度下降算法也随之不断的发展。传统的梯度下降算法存在无法收敛到全局最优，并且在收敛过程中陷入振荡的问题。为此，在下降过程中引入动量因素，一定程度上可以解决振荡问题［24］。Nesterov［25］提出了一种新的动量下降方式，进一步改善了优化过程中的振荡问题。Dean［26］和Duchi等［27］提出一种具有初步的自适应学习率的梯度下降算法，通过累积历史梯度的方法，改善了学习过程当中固定步长带来的不收敛问题［28］。Kingma和Ba［29］提出了著名的适应性矩阵估计（Adaptive Moment Estimation）算法，通过结合自适应学习率和动量的算法，实现了一种新的梯度下降算法。在凸优化当中，改进的梯度下降算法已经可以非常高效地收敛到最优值。故而本文在此采用具有自适应学习率带动量的梯度下降算法进行优化。

在之前的研究当中，鲜有学者应用人工智能优化设计方法来求解起落架收放装置路径的问题，为了弥补相关研究的不足，本文提出了一种自动求解起落架回收路径的方法。首先，讨论并分析了起落架回收的运动形式，并建立了相应的运动学模型，得到了起落架的转轴分布规律。然后，给出了表示起落架和机舱环境的几何信息以及计算两者之间相对距离的方法，建立了相关的优化模型。最后，以某一高超声速飞行器的起落架收放机构设计为例开展智能设计，并讨论了模型划分精度对最终结果的影响，验证了理论模型的可行性。

1 起落架的收放路径寻优方法

1.1 起落架的收放形式

从收放的角度看，飞机的起落装置主要由主支柱、收放机构、起落架舱段3个部分构成。其中，主支柱由缓冲系统及机轮组件构成整体参与收放动作，由于缓冲器和机轮需要承受飞机较大的进场冲击和减震的任务，其体积往往较大，占据了起落架的绝大部分体积，并且主支柱是收放过程当中需要竭力去避免与舱段结构发生空间干涉的部分。对于执行起落架收放的运动机构而言，虽然这一部分占据体积较小，但主支柱的收放形式及运动路径是由运动机构决定的。而位于机身内部的起落架舱段，其空间形状和收藏位置决定了起落架的运动轨迹限制和收上位置条件。

目前，起落架的收放方式主要是平面收放以及空间收放2种方式。平面收放依靠四杆运动机构驱动起落架在空间中作圆弧线运动，而空间收放方式则依靠更加复杂的驱动机构实现起落架的空间三维运动。但是无论是平面机构还是空间机构，驱动起落架运动时起落架的末端所划出的轨迹均可视为一条球面弧线。而起落架的主体部分支柱及轮胎的收放运动所产生的扫掠体对于平面运动机构而言是一圆面，对于三维空间机构则可以视为圆锥面的变形体，如图1和图2所示。总的来讲，可以将起落架的空间收放过程视为绕某根主转轴进行转动的过程。运动路径设计就主要着眼于在确定的收藏空间以及确定的工作位置下，寻找合适的转轴。

图1 起落架的收放过程示意图Fig.1 Schematic diagram of landing gear retraction and extension process

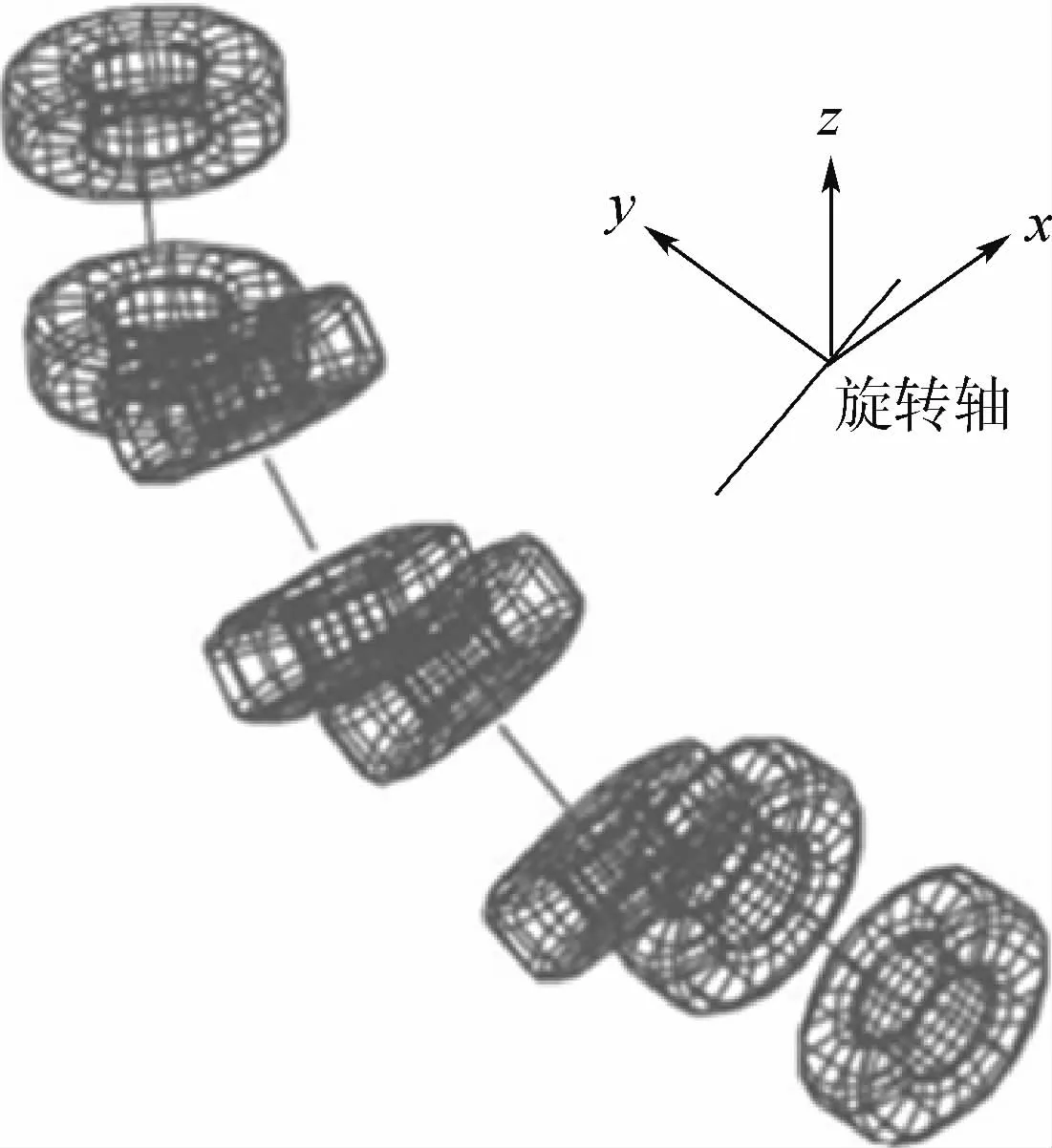
图2 起落架运动过程中产生的扫掠体示意图Fig.2 Schematic diagram of swept body generated during landing gear movement

起落架所受到的主要约束在于必须保证起落架的收放过程不与机身舱段的任意部分发生干涉，并且能够使得起落架在收起过程中与飞机舱段的几何边界的距离最大化。故而本文建立起落架收放的运动学模型，得到起落架几何信息表示，运用三角网络的相互距离进行碰撞的检测与度量，通过梯度下降算法进行运动路径的分析与设计。

1.2 起落架收放运动学模型

起落架及附近机舱环境真实机构零件众多，结构连接复杂，为便于进行优化分析，同时不使模型过于理想化偏离实际，对于起落架支柱、收放装置以及机舱环境作出如下假设：

1）将执行起落架收放的收放装置，以及承受冲击的机轮、支柱简化为一个整体构件，将其视为由一近似圆柱体以及两机轮所组成的几何体。

2）将航空发动机、进气道等共同组成的复杂机舱环境统一视为一个整体，对于复杂的连接部分以包络体代替。

3）在起落架回收过程当中，不考虑机舱环境本身的变化，也不考虑安装点位置的变化。

对于整个优化过程，建立坐标系如图3所示。

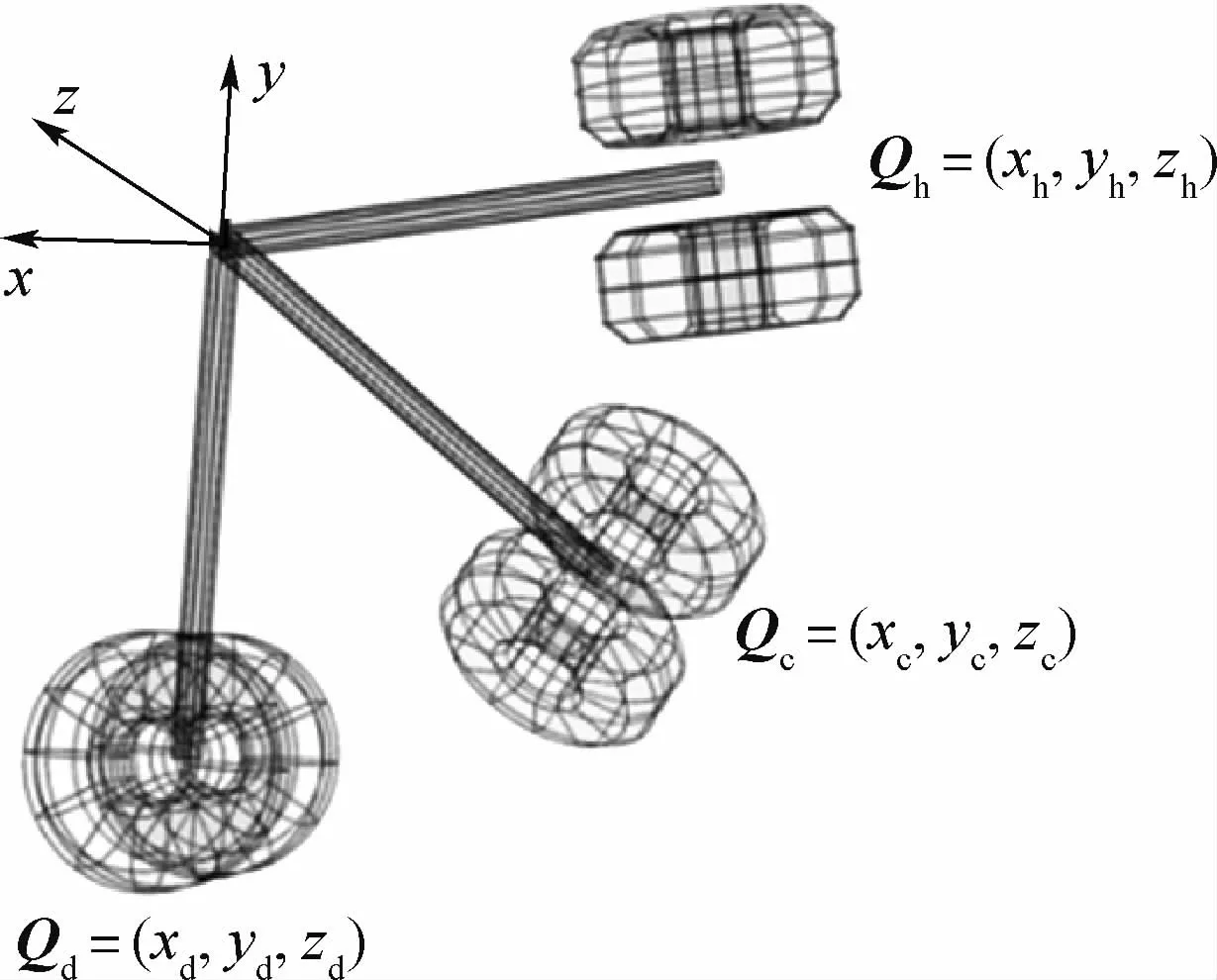
图3 坐标与位置向量示意图Fig.3 Schematic diagram of coordinate and position vector

以起落架在放下状态时主支柱的中心轴方向作为y轴方向，垂直于y轴的向前方向作为x轴方向，两机轮中心点的连接线作为z轴方向，以起落架的安装点作为坐标原点，建立全局坐标系。

在全局坐标系下，对于确定安装点与放下状态的起落架在空间中所处的位置，可由其末端位置的坐标决定。起落架处于放下状态时，其末端的位置由向量Qd＝（xd，yd，zd）表示，其中xd、yd、zd分别表示放下状态时起落架末端位置在全局坐标下的x、y、z坐标值。起落架处于收起状态时，其末端的位置由向量Qh＝（xh，yh，zh）表示，其中xh、yh、zh分别表示收起状态时起落架末端位置在全局坐标下的x、y、z坐标值。

起落架处于收放过程中任意位置时，其末端的位置坐标可以由向量Qc＝（xc，yc，zc）描述。

对于确定的起落架放下位置与收起位置，能使得起落架从放下位置旋转到收起位置的所有旋转轴，必定分布在收起位置向量和放下位置向量的角平分面上，如图4所示。该平面通过安装点即坐标原点，其法向量可以表示为

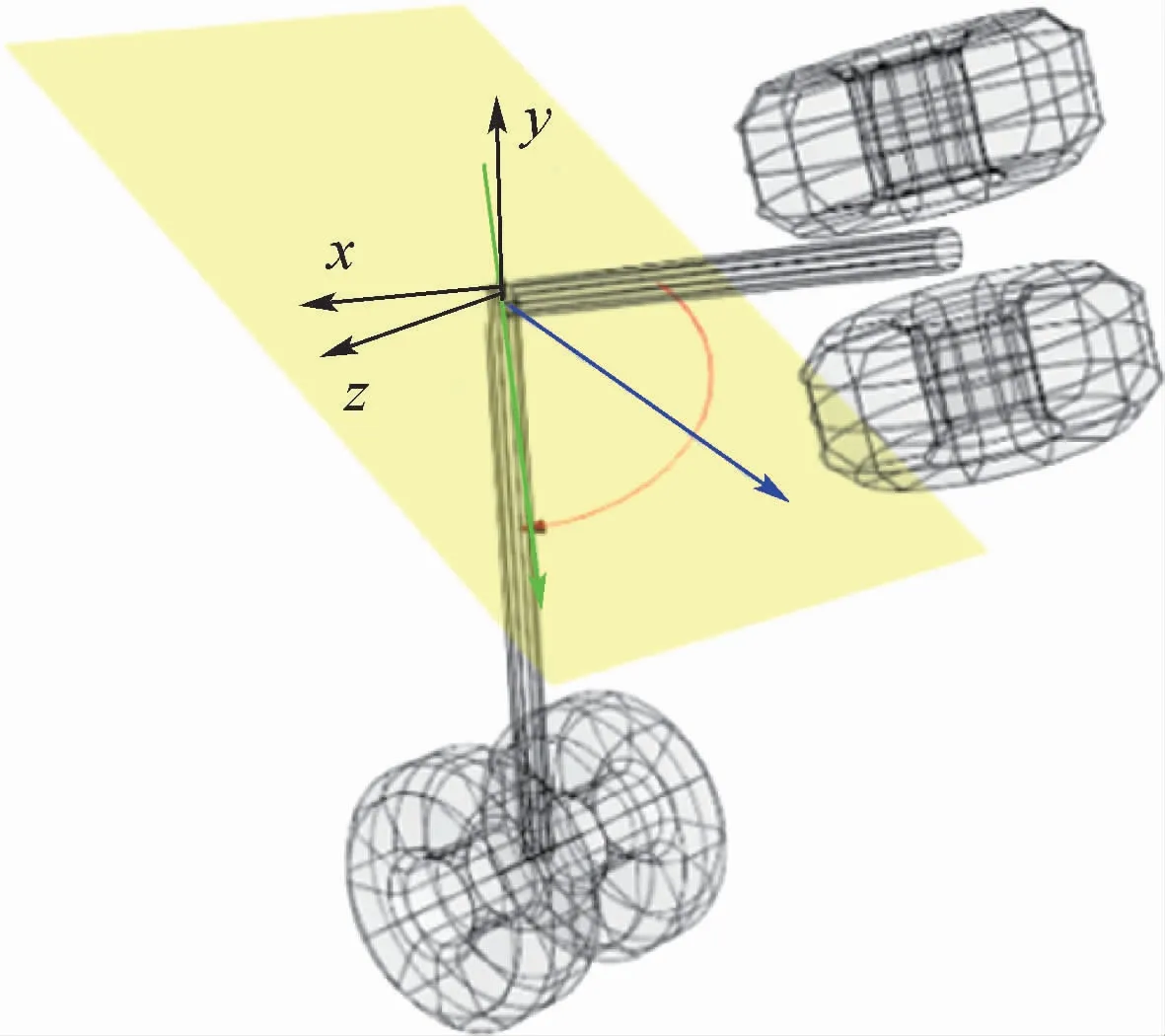
图4 转轴分布平面Fig.4 Shaft distribution plan

所有满足条件的旋转轴，其相应的单位向量R（xr，yr，zr）必然分布在这一角平分面上，满足：

式中：ρ为单位长度旋转轴在全局坐标xy平面上的投影长度；xf、yf、zf为起落架所处平面法向量的分量；θ为单位长度旋转轴在全局坐标xy平面上的投影与x轴所夹的角度，在该参数确定的情况下，可以完全确定起落架的旋转轴。

1.3 起落架几何体及相互距离的描述

为了进行起落架收放路径的优化设计分析，需要对起落架及机舱环境的三维模型进行描述与表示，在此基础上计算相关几何信息作为优化值。三维模型的表示方法主要有以下4种：深度图方法、点云方法、体素方法以及网格方法，如图5～图8所示。

图5 深度图方法Fig.5 Depth map method

图6 点云方法Fig.6 Point cloud method

深度图方法无法获得完整的三维信息，点云的表示方法具有稀疏性，且对于本文所选取的优化变量来说，具有额外的内部点，难以直接获得表面信息。故而在这里采用三角网格表面剖分的方法描述起落架及机舱环境等几何体。

STL文件是一种用于存储三角网格的文件格式，其通过储存每一个三角面片的顶点信息，以及该三角面片的法线信息，实现对三角网格的储存。用于STL文件的三角网络，需要满足以下要求：①每个三角面片必须与其相邻的三角面片共享2个顶点；②所有三角面片的法线方向必须朝外。因此，三角网络必须是封闭的，有可以明确定义的不相连通的内部与外部。在起落架的收放路径设计分析当中，无需考虑起落架的材料信息、力学信息以及表面纹理等特征。使用该文件格式储存，可以以较小的文件大小获得完整的表面几何信息，并且实际飞机的三维模型可以轻松地从大型三维设计软件所生成的商业三维模型文件转换为STL文件。通过设定代表三角面片与真实曲面之间距离的弦高，以及控制三角面片夹的角度可以较为轻松地控制划分精度。

典型的STL文件储存的三角网格，可以视为由n个较小的三角面片以及文件头信息组成，其中每个三角面片当中储存如下格式数据：

在优化过程中，要度量2条不同的运动路径之间的优劣，需建立一个能够比较当前运动路径与其他运动路径优劣的指标，并且该指标具有较好的优化性能，且能够很好地体现设计目标。本文中，将起落架在收放过程中与机舱环境之间的最近距离作为评价该条运动路径的指标，在具体实现中，用机舱环境的三角网格与起落架的三角网格之间的距离作为优化的度量。2个三角网格之间的距离考虑为三角面片所组成的集合之间的距离，即2个集合当中距离最近的2个三角面片之间的距离：

式中：A为起落架三角网络；B为机舱环境三角网络；a为起落架当中的面片；b为机舱环境中的面片。

1.4 运动路径的优化设计

具有确定的放下位置和收起位置时，起落架主转轴的方向可通过式（7）由单个参数θ予以决定，该参数的取值范围在有限区间［0，2π］上。故仅需要考虑在该有限区间上取得最优的参数，可以得到最合适的主转轴。

考虑起落架从放下位置收起到收藏空间的全过程中与机舱环境等障碍物之间的最短距离作为评价该回收路径的指标，在收放过程当中通过判断起落架当前位置向量Fc与目标位置向量F之间的夹角β的余弦函数值cosβ作为判断起落架是否收藏到预计目标空间的依据。

在具体的实现当中，通过设置围绕代表旋转轴的单位向量R＝（xr，yr，zr）的旋转矩阵：

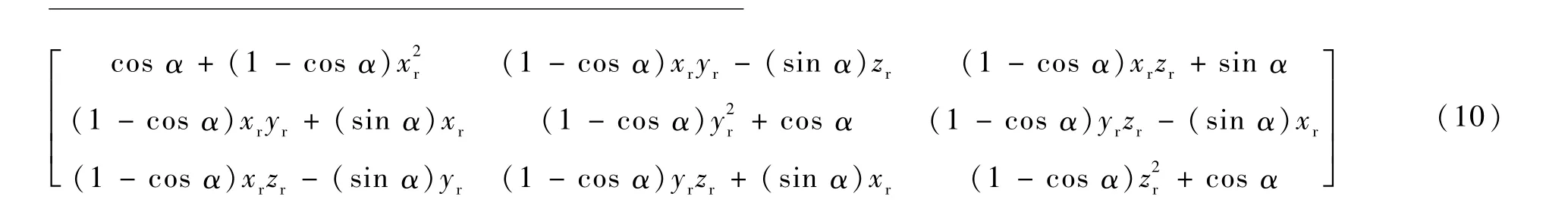
该矩阵使得起落架每次旋转特定的度数α。在每次旋转过后计算起落架与机舱环境之间的最小距离dis，并且判断其当前位置向量与目标位置向量之间夹角的余弦函数值cosβ，当满足cosβ≥1-ε，认为起落架已抵达目标位置，其中ε为一个正的小量，一般取为1-cosα，以规避起落架非连续旋转所带来的误差。

故而针对在具有确定的收起状态和放下状态的起落架回收路径设计，可以等效为如下优化模型：

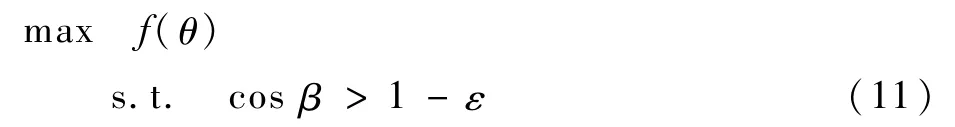
式中：函数f（θ）表示沿参数θ所确定的回收路径运动时起落架与机舱环境之间的最短距离。控制条件要求沿该回收路径运动必须能够抵达目标位置。对单参数θ的优化可以通过简单的梯度下降或者搜索较为快速地获得全局最优解。但是在给定收起位置与放下位置的情况下，最优解未必满足起落架与机舱环境之间存在足够间距的设计条件，需要考虑起落架在收藏空间中不同的放置状态，故而在这里需要对目标位置向量进行优化。

起落架的目标位置向量是一个三维向量Qh＝（xh，yh，zh），但考虑起落架杆长长度L一定，存在一个约束x2h+y2h+z2h＝L2，因此，实质上该问题是二维优化问题。

为消除该约束，将起落架目标位置向量归一化过后，可以通过方向角-笛卡儿坐标转化公式，将起落架的坐标转化为方向角坐标（又称球坐标）描述：

式中：L为起落架的长度，当模型给定时，L是一个定值；θ，φ为方向角，用于确定向量的方向。

以给定初始期望的收起位置作为起始条件，对该位置向量向四周延伸一定弧度r的区域，作为优化范围。

所有可能的解在空间中将构成一个锥形区域，如图9所示。对于某一个确定的收起位置，考虑当前位置条件下，计算得到最优的回收路径，作为当前位置的最优路径。通过比较不同收起位置的最优回收路径所对应的最短距离值，优化收起位置。可以得到如下优化模型：

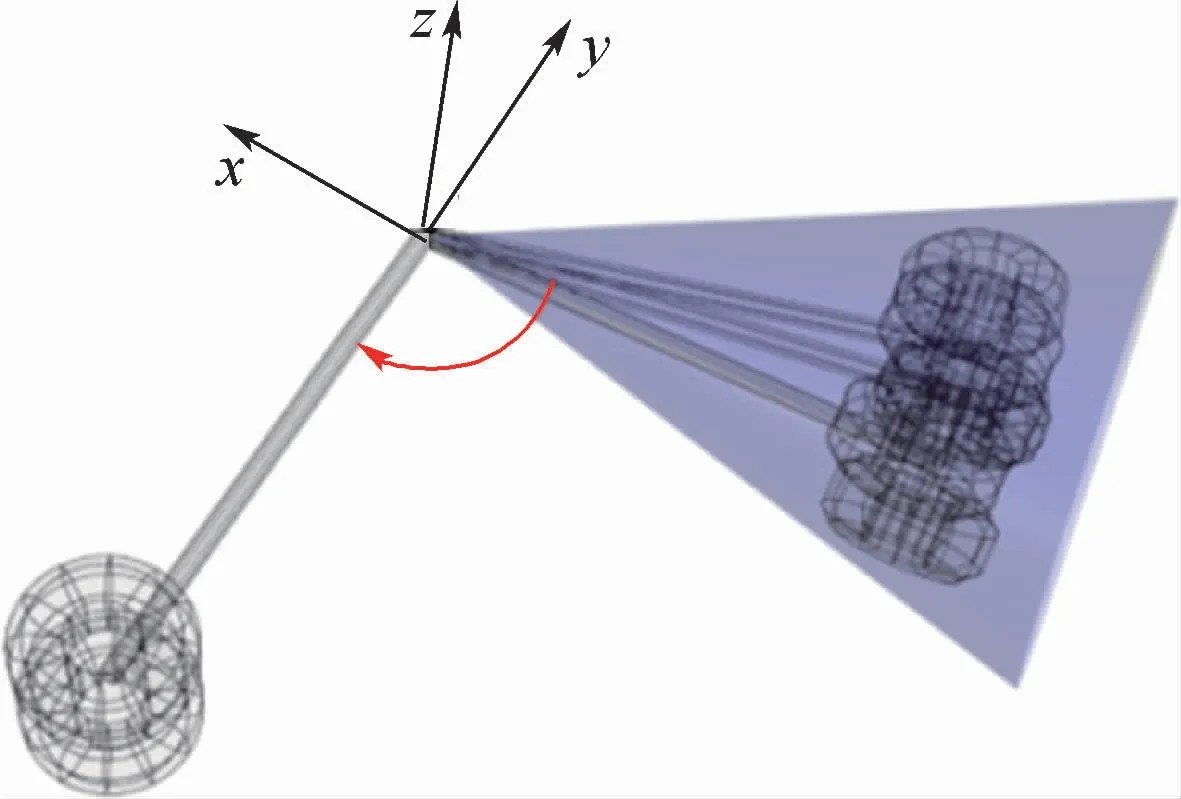
图9 可能解构成的区域Fig.9 Regions of possible solutions

式中：函数f（θ，φ）表示在选取方向角θ与φ的情况下，起落架能够抵达该目标位置的最优路径的最短距离。控制条件则要求目标位置偏离期望目标位置方向角度，必须在所限制的一定弧度r内。

ADAM算法是一种通过结合动量梯度下降与自适应学习率方法所形成的一种新型的用于优化深度神经网络的梯度下降算法。该算法适用于解决非凸优化问题，易于实现高效计算且能够很好地处理非稳态问题，超参数可以得到直观解释。对于优化起落架在目标收藏空间当中的放置位置这样一个二维非凸的优化问题而言，具有良好的特性。通过该算法来优化所建立的运动学模型，主要需要调节的超参数为学习率。

2 计算案例

以某一高超声速飞行器的起落架收放机构设计为例，开展起落架运动路径的优化设计计算。该飞行器的进气道结构、机载设备及隔热层设计使得起落架收藏空间极为狭窄，致使起落架的收放路径设计非常困难。该案例的模型简化如下：对于起落架本身，通过简化不必要的附加机构，仅保留其支柱及轮胎部分，得到如下模型。对于由进气道与航空发动机及飞机外部的蒙皮等所共同组成的复杂机舱环境，通过截取起落架安装位置部分的舱段，考虑舱门处于打开状态时，通过包络体覆盖复杂的连接部分，过后得到如图10所示机舱舱段。

图10 机舱舱段模型Fig.10 Cabin model

以起落架的安装点，即起落架支柱的末端位置作为全局的坐标原点，建立如图11所示的坐标系。主支柱的中心轴方向为y轴方向，垂直于y轴的向前方向作为x轴方向，两机轮中心点的连接线作为z轴方向。

图11 起落架模型Fig.11 Landing gear model

起落架的收起和放下位置如图12所示，这里的收起位置是由飞机总体设计给定的目标位置，坐标值为（2 201.37，1 180.98，-94.09）mm，而相对的起落架放下位置坐标为（0，0，2 500）mm。

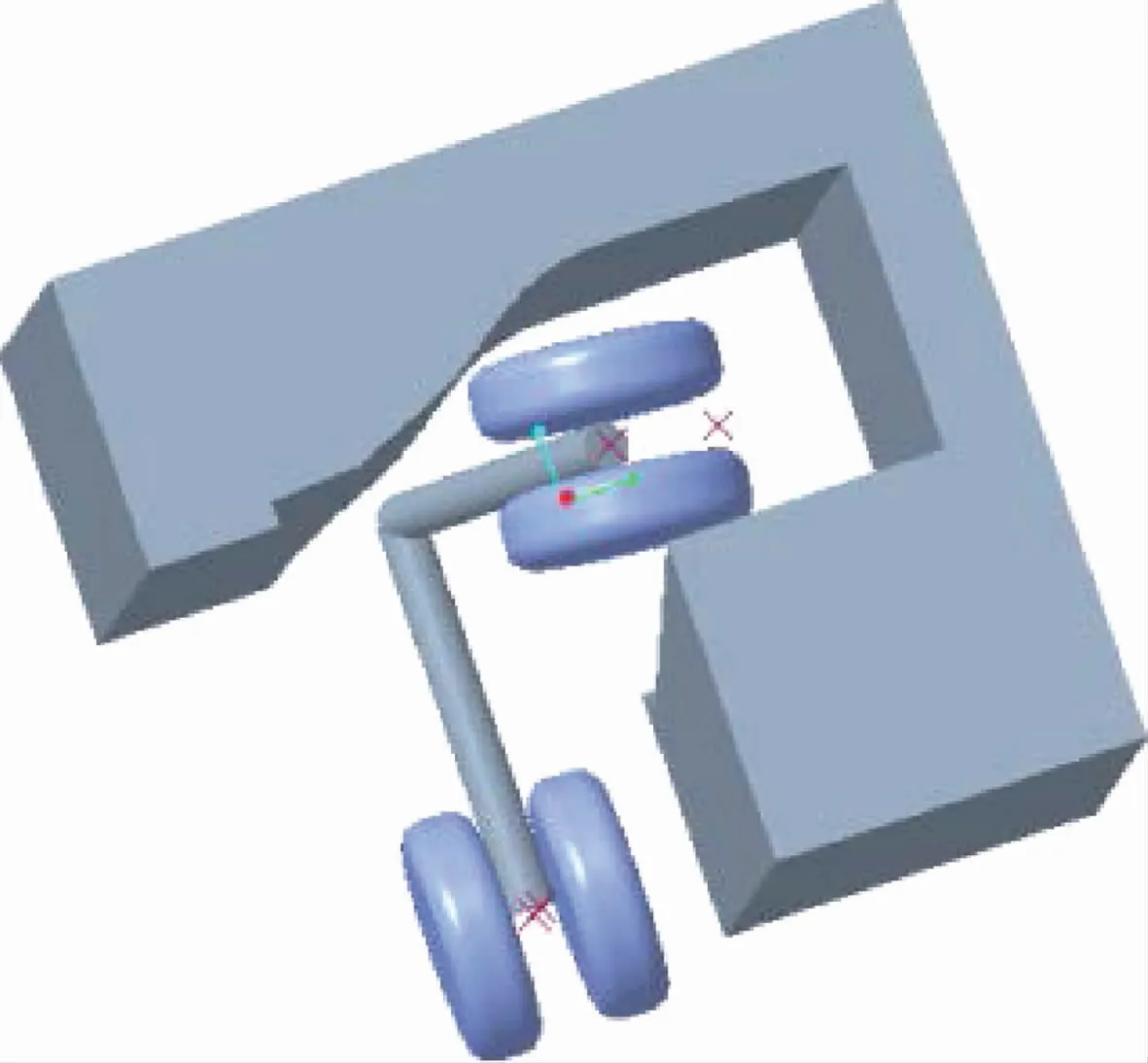
图12 收放位置示意图Fig.12 Schematic diagram of retraction and extension position

利用creo paramicas软件对于所得到的起落架模型及障碍物舱段模型进行网格划分，导出成为STL文件，生成三角网格模型。这里需要指出的是，STL的网格化精度对于最后计算精度以及速度的影响也是不可忽视的，为了说明网格精度对结果的影响，这里以低精度和高精度2种情况进行说明。

图13～图16为三角网格低精度（面片数较少）划分与高精度（面片数较多）划分。图13和图14分别表示起落架舱段低精度和高精度网格划分示意图，低精度以角度与弦高分别为0°和2 558 mm划分为138个面片，高精度以角度与弦高分别为0°和15 mm划分为634个面片。图15和图16分别为起落架低精度和高精度网格划分示意图，低精度以角度与弦高分别为0°和2 335 mm划分为88个面片，高精度次角度与弦高分别为0°和245 mm划分为158个面片。

图13 低精度的舱段划分Fig.13 Low-precision cabin division

图14 高精度的舱段划分Fig.14 High-precision cabin division

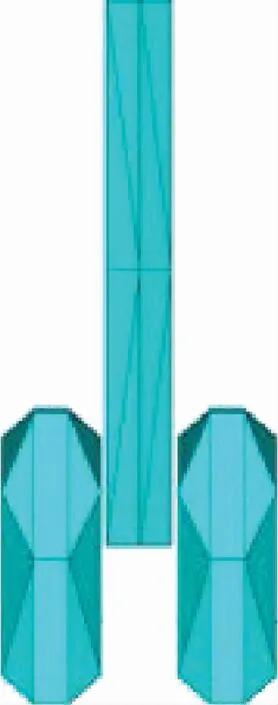
图15低精度的起落架划分Fig.15 Low-precision landing gear division

以理想的收藏状态位置向量（2 201.37，1 180.98，-94.09）mm作为目标位置，建立单参数优化模型，由式（2）可以得出转轴分布平面的法向量为（-0.613 3，-0.327 9，0.720 3）mm。因此，通过该平面的法向量可以由式（7）得到起落架的转轴。将舱段和起落架以不同划分精度进行交叉组合，应用所建立的优化模型进行计算分析，得到如表1所示的结果，其中最优参数为起落架的旋转轴空间角。

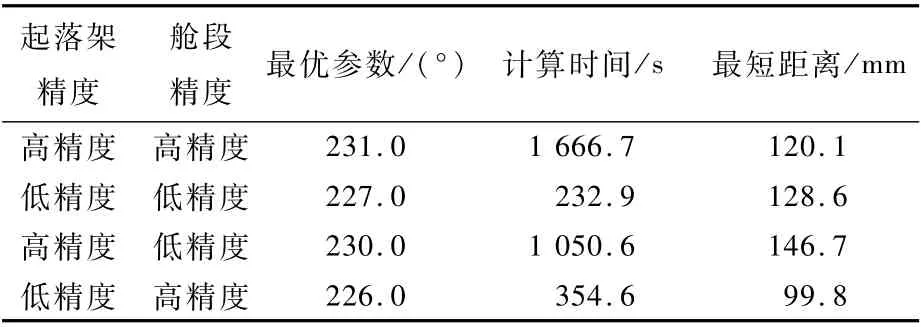
表1 应用不同的划分方式得到的结果Table 1 Results by different partition methods

由分析结果可知，面片精度的高低确实会影响三角面片距离的计算精度，但只要在低数量的面片网格不影响起落架及舱段结构体几何形态的前提下，对于起落架收放空间轴的计算结果就不会有本质的差异。但是，面片精度较低的模型的计算效率明显高于高精度划分的模型，这一结论对于降低复杂结构体间运动干涉的计算量具有非常重要的意义。

在考虑机舱环境为单开口的情况下，观察随着参数θ的变化所得到的回收路径的最短距离结果，可以看出，在给定收起位置和放下位置的情况下，对绝大多数参数θ的取值而言，起落架无法回收到收藏空间，最短距离为0 mm。仅当θ取值在某个区间上时对应的回收路径可以使起落架穿过开口，不与机舱环境发生干涉而抵达目标位置。在该区间上对参数θ的优化模型可以视作是凸优化，该类问题可以通过多点启动的全局寻优快速获得最优值，即最短距离的最大值，进而得到相应的收放路径。

图17的结果虽然已经满足了设计条件，但是仍具有改良的空间，在这里使用二维优化模型，寻找更好的回收目标位置。

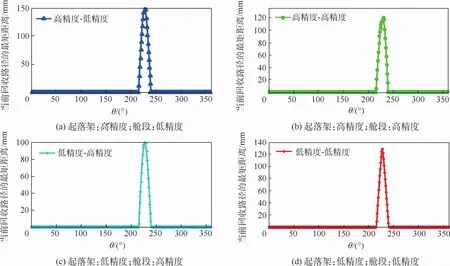
图17 回收路径的最短距离与参数θ的关系Fig.17 Relationship between the shortest distance of retraction path and parameterθ

通过方向角-笛卡儿坐标转化公式，可以得到当前理想目标位置的方向角坐标为（28.21，-2.150）mm，以此处作为梯度下降的起始点，运用ADAM 算法进行优化，选取不同的学习率，可以得到如表2所示的结果。

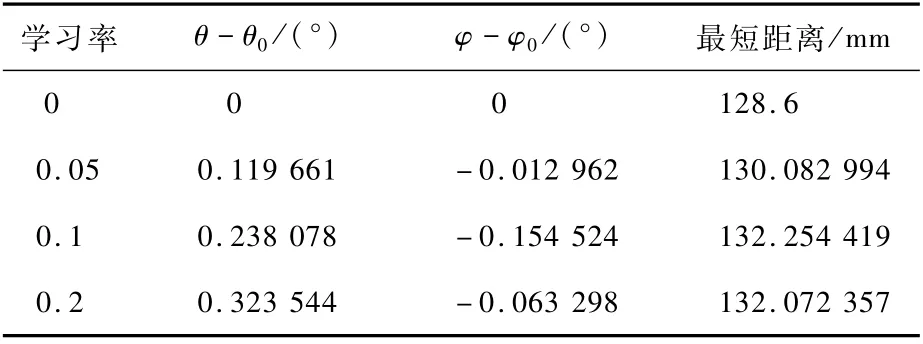
表2 选取不同优化参数得到的结果Table 2 Results by selecting different optimization parameters

表2中对比了不进行二维优化（即学习率为0）和使用不同学习率进行二维优化在用ADAM算法迭代一定轮数过后的结果。可以看出，相比于不进行二维优化，进行二维优化过后，最短距离有所增长，而相比原始目标位置角度偏离不大。当学习率取于0.1～0.2之间，优化所得的结果趋于稳定。

3 结 论

本文针对起落架收放轨迹的优化问题，提出基于智能优化算法的起落架复杂机构自主设计方法，获得了起落装置的最优收放轨迹，相关结论如下：

1）为了求解出最优的起落架收放轨迹，先后建立了起落架的运动学模型，运用STL文件、最短距离检测的方法，实现了起落架的几何信息表示及碰撞检测。建立了针对起落架回收的优化模型，给出了利用ADAM进行优化的方法。以某一高超声速飞行器起落架收放部分舱段为例，对比了不同学习率和划分精度对寻找起落架最优位置及相应收放路径的影响，最终寻找到了该例中最优的收起位置和相应的收放路径。

2）提出了基于智能化设计来解决起落架收放轨迹优化的方法，并以某狭窄的机舱环境为例进行了相应的智能优化设计，对比了传统的设计方法。本文飞机起落装置收放轨迹智能设计方法能够切实提高起落装置收放轨迹的设计效率和性能，实现起落装置收放轨迹的快速设计和最优设计。

3）经过对不同划分精度的对比，本文智能设计方法对划分精度的容忍敏感度较低，可以以较快的速度在误差范围内完成设计。而通过设置0.1～0.2的学习率对收藏位置进行优化，可以使得起落架相对人工给定的位置，以不超过0.5°的偏离，获得起落架和机舱环境距离4～5 mm 的提升。