基于复杂网络的证券市场智能建模与分析*
2022-01-15李双宏舒子宸肖雅雯
李双宏 舒子宸 肖雅雯
(1.东方证券股份有限公司系统研发总部 上海 200010)(2.哥伦比亚大学梅尔曼公共卫生学院 纽约 10032)
1 引言
对股票市场的建模与分析主要从20世纪五十年代开始。Harry M.Markowitz在1952年提出了均值-方差组合模型,通过协方差来衡量股票间的相关性[1]。随后的数十年,研究者大多对影响股票价格的因子进行了进一步研究,其中以William F.Sharpe的夏普单指数模型[2]以及Eugene F.Fama和Kenneth R.French在1992年提出的三因素模型[3]最为著名。在衡量股票间相关程度时,主要通过Pearson相关系数和归一化互信息这两种方式。而在构建股票市场网络时,国内外学者对最小生成树法(MST),最大平面过滤图法(PMFG),阈值筛选法,随机过程以及随机矩阵理论等方法均进行了尝试和研究,成功地揭示了股市的某些运行机理,并对各网络构建方法的优劣势作了全面的对比。
由于MST和PMFG存在破坏股市内部结构和股票间的关联信息以及边信息大量损失问题[4~5],不便用于考察股市网络的动态演化情况,近年来,研究者开始改用阈值筛选法来进行股票市场网络的研究。相较于前两种方法,阈值筛选法更为简单易用。在阈值筛选法中,股票节点的连边保留与否取决于其与设定阈值的比较关系。同时,社团划分算法的提出和发展也为对股票市场网络的分析提供了新的方法,其中被广泛应用的有Newman的fast greedy算法[6],Pascal Pons的walktrap算法[7]和Vincent D.Blondel等的BGLL算法[8]。文献[9~12]中已证明以上算法能够有效发现股票市场中的社团结构。
以往研究中[13~14]均使用的是日收盘价数据,且在描述股票间关系时所选取数据的时间跨度常为数百个交易日,反映的是股票市场中主要指数成分股长期的变化情况。为了能够有效观察到股市中短期的演化情况,本文将尝试从已取得较好效果的阈值筛选法出发,改进方法,调整参数,探索构建基于日内数据的涵盖整个股票市场的时序动态网络,并分别使用fast greedy,walktrap和BGLL算法进行社团结构分析。本文的主要创新点在于:
1)将对股市网络的研究对象扩展到整个股票市场中的所有股票,而不再限于指数的成分股集合或部分板块。过往的研究者多关注构成主要市场指数的成分股和具有相同特征的股票集合,如大市值股票,某板块内股票。如此构建股市网络虽能够在一定程度上保留市场整体信息的同时减少构建过程中的计算复杂度,却往往忽略了市场中处于“边缘”的股票对网络结构的影响。为尽可能保留市场价格信息,本文选择构建针对全股票市场的网络,并将所有股票纳入到分析研究的范围中。
2)利用日内价格数据构建能够反映市场中短期行情变化的股市网络,并在此基础上采用多种社团划分算法进行社团结构分析。上述研究所用数据均为日收盘价数据,着眼于股票市场的长期网络结构演化情况。鉴于本文的研究目的之一是为投资决策提供参考,因而改用日内价格数据以更好地捕捉中短期的市场变化。
3)选用了研究中常用的fast greedy,walktrap和BGLL三种算法进行网络划分,采用Salton,Jaccard和Sorenson相似性指标,并自行设计和提出了继承比这一相似性指标,在网络结构分析的同时比对三种划分算法的优劣,从中选出最优者用于以后的分析研究。
2 股票市场时序动态网络构建方法
假设时序动态网络中包含N只股票,当前片层对应的观测时间区间为[t0,t0+T]。在观测区间的任一时点τ股票i的收益率为

其中,股票i在τ时段的价格(收盘价或均价)为Pi(τ),上一个时段的价格(收盘价或均价)为Pi(τ-Δt)。
在获得了该观测区间内所有股票的收益率序列后,计算股票间的Pearson相关系数pij(t0),即有:

其中,ri和rj分别为股票i和股票j在该观测时间区间的对数收益率序列,E(ri)和E(rj)分别为股票i和股票j在该观测时间区间的收益率数学期望;对于加权时序动态网络,该片层下节点i和节点j之间的连边权重即为ρij(t0);而对于阈值筛选法下的无权网络,连边存在与否通过与阈值进行比较决定。
3 股票市场加权网络构建和社团分析
选取2019年10月8日至2020年3月31日A股股票30分钟均价数据,涉及3809支股票,共计952个交易时段记录。采样步长以使得网络参数同全市场指数变化的相关性最大,从而能够有效反映股票市场网络演化为选取标准,计划分别选择ΔT=24个交易时段和ΔT=8个交易时段来进行测试,最终选定能有效反映网络演化过程的为步长。先进行数据对齐,时间窗口内按第二部分所述方法计算股票间相关系数。两个不同步长下,股票间相关系数均值变化如图1和图2所示。

图1 步长为24个交易时段网络平均相关系数与市场指数走势对比

图2 步长为8个交易时段网络平均相关系数与市场指数走势对比
当步长ΔT=8个交易时段时,相关系数为-0.5540,同步长ΔT=24个交易时段时的结果相差无几。对于所构建的网络,再分别利用fast greedy社团划分算法来进行划分,发现社团个数基本维持在2~3个左右,且在输出社团内节点个数进行观察后可知,绝大多数股票集中于几个大规模社团中,这符合社团个数保持相对稳定这一要求。最后,为判断所构造的时序动态网络是否满足能有效地观察到演化过程这一要求,最为重要的标准之一便是评估动态网络各片层间对应社团的相似性(继承性)。采用基于局部信息的节点相似性指标:Jaccard指标,Salton指标和Sorenson指标,来设计和选取社团相似性指标,并将所对应数据从节点相关扩展至社团相关[15~16]。

在式(3)~(5)中,A1为上一时间窗口(片层)中的社团,A2为本时间窗口(片层)中继承自A1的社团;Γ(A1)为前一时间窗口下社团A1内的节点集合;Γ(A1)∩Γ(A2)代表社团A1和A2的交集内节点个数;kA1为社团A1内的节点间度值之和。此外,为了更直观的体现所在时间窗口下的社团同所继承的社团之间的节点相似程度,本文中另设计继承比率这一指标,其定义式如下:

对于相邻时间窗口(片层)的社团继承关系的确定,判定原则为对于后一时间窗口内的一个社团,遍历其与前一时间窗口下的所有社团的交集,认为其继承自与其交集内节点数目最大的前一时间窗口下社团。
考虑到步长ΔT=24个交易时段时的股票市场加权网络同股市整体价格变化的相关性更大,先对其进行社团划分和社团结构分析。首先利用上一章中fast greedy社团划分算法所得到的结果进行片层间相似性分析,相关指标的变化如图3所示。

图3 步长为24个交易时段fast greedy算法划分后社团相似性指标变化
在每一个时间窗口,对于其划分所得的各个社团分别计算上述四个指标,而后进行加总平均,最终所得均值展现在了图3中。需要特别说明的是,计算所得的Salton和Sorenson指标值过小而不便于比对,因而进行分析时分别对其数值乘上100予以放大,随后的相似性分析中也将采用同样的操作。根据Salton指标和Sorenson指标的定义式可以发现,要使得两个指标的数值相近,应使得被考察的两个社团在节点度值之和上近似相等。对于继承比率和Jaccard指标而言,指标构成仅仅与节点相关,当且仅当所考察的社团的节点组成大致相同时,两个指标才能取得较大数值。而从图3中不难看到,Salton指标和Sorenson指标在2019年10月到2020年3月近半年的时间跨度中维持了近似相等的状态,说明从度中心性的角度进行考量,片层间社团的相似性较高。然而,从继承比率和Jaccard指标来看,社团的相似性较低,这说明从社团内节点集的角度出发,片层间社团的继承关系不够明显。
使用fast greedy算法所得社团划分结果在良好反映网络动态演化过程这一评价维度上表现不够理想,认为可能和所使用社团划分算法分辨率限制等不足有关[17],因而尝试使用另外两种基于模块度的划分算法——walktrap和BGLL算法来进行社团划分,而后对当前网络片层间的相似性进行分析。两种算法划分结果在不同时间窗口下非单节点社团个数均在2到8个之间波动,保持了相对稳定。至于划分结果的社团相似性,相关指标展示如图4和5所示。从Salton指标和Sorenson指标来看,两种算法基本保持了Salton指标和Sorenson指标的近似相等,度中心性维度上的社团相似性较高。从继承比率和Jaccard指标来看,片层间相对应社团的节点相似性依旧较低,这意味着对于个股而言,其难以长时间处于对应的社团中,这不利于基于时序动态网络社团划分结果的高稳定性股票选取和权益组合构建。类似的结果在表1中得到了印证。在表1中,给出了不同社团划分算法下,从2019年10月到2020年3月的38个时间窗口下相关指标的均值。继承比率和Jaccard指标表征的节点相似性在三种不同的社团划分算法中均录得较低值,这已然证明了股票市场时序动态网络中特定社团无法长期稳定存在,ΔT=24个交易时段的步长过大,不利于观察股市网络的动态演化过程。

图4 步长为24个交易时段walk trap算法划分后社团相似性指标变化

表1 步长为24个交易时段不同社团划分算法下社团相似性指标均值
现对于步长ΔT=8个交易时段所构建的股票市场加权网络进行社团划分和社团结构分析。同样地,先利用fast greedy社团划分算法结果进行片层间相似性分析,Jaccard等四个指标的变化图如图6所示。

图5 步长为24个交易时段BGLL算法划分后社团相似性指标变化

图6 步长为8个交易时段fast greedy算法划分后社团相似性指标变化
对应地,步长ΔT=8个交易时段的股票市场加权网络在不同社团划分算法下片层间相似性指标结果如表2所示。

表2 步长为8个交易时段不同社团划分算法下社团相似性指标均值
同ΔT=24个交易时段所构建的股市网络相比,当前加权网络进行社团划分后Salton指标和Sorenson指标仍近似相等,从度中心性的角度而言,保持了较高的相似性;同时,继承比率和Jaccard指标也在半年的时间段内始终处于较大数值,这说明从对应社团的节点构成而言,相似性有了明显提升,即意味着能够更为细致而准确地观察到股票市场加权网络的动态演化过程,并根据继承关系从中选取符合相关条件的稳定性较高个股。这里给出从2019年11月11日到2019年11月20日期间相邻的四个片层(时间窗口)的社团划分结果,使用gephi软件,通过Force Atlas算法实现可视化,如图7所示。不同图中涂色为橙色,绿色和紫色的社团存在着继承关系,即下一张图中的某颜色社团继承自上一张中的同色社团。可以看到,尽管存在着社团的演化,但绝大多数为一个大规模社团的拆分和合并,如图7(d)中淡蓝色涂色社团即继承于图7(c)中橙色社团,继承比率为61.68%,因而依旧能够保持较高的相似性。


图7 社团划分结果
此外,社团划分结果同行业分类也密切相关。从整个时序动态网络中随机抽取三个片层,分别为2019年12月20日 到2019年12月26日 的 片 层,2020年1月14日 到2020年1月20日 的 片 层 和2020年2月19日到2020年2月25日的片层。获得这三个片层在fast greedy算法下的社团划分结果,取出其中规模最大的两个社团,社团内节点个数如表3所展示。可以看到,片层中绝大多数的股票节点均集中在最大的两个社团当中。
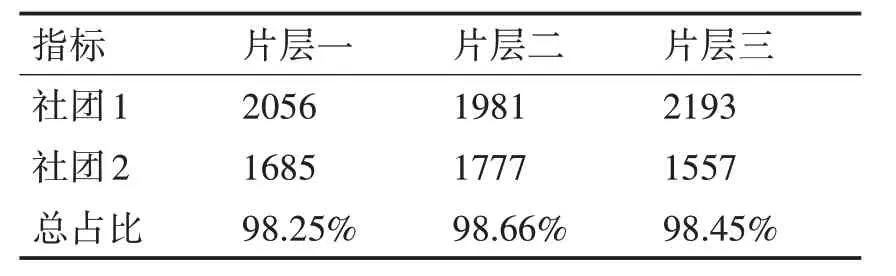
表3 片层内社团股票节点个数及总占比
行业分类参照的是证监会2019年第四季度的行业分类表,并将包含股票过多的制造业拆分至二级分类进行行业结构分析。对于社团内出现的2020年上市股票,则被列入无法识别这一类别。在计算社团内股票在各行业占比时,使用的是该社团内归属于某行业的股票节点个数与某行业的股票总个数的比值。不难从表4和表5的对比中发现,在抽取所得的片层中,虽然最大的两个社团内部的节点个数相差并不大,但两者内部股票节点的行业构成差别明显,且在本文的测试时间段内保持了相对的稳定。这不仅证明了社团划分的有效性,而且不同社团内股票的类别差异也能够为分散化投资提供参考。
4 结语
本文通过将股市网络的研究对象扩展到所有股票,而非限于指数的成分股集合或部分板块,更加充分地挖掘市场“边缘”股票对网络构建的影响信息。创新性地选用了日内均价数据来构建涵盖整个股票市场的时序动态网络,观察股票市场网络在短期内的社团结构性质和演化过程,捕捉中短期市场变化。针对阈值筛选法所得网络存在不连通等问题,提出直接构建基于价格数据的Pearson相关系数的股票市场加权网络。在确定股票市场加权网络参数和短期市场走势相关后,设计提出改进的继承比相似性指标,与Jaccard和Salton等片层间社团相似性指标更为全面地分析网络构建与社团划分的有效性。最终选定了较好的加权网络步长参数和所使用的社团划分算法。根据所得结果,基于日内均价数据的Pearson相关系数所构建的股票市场加权网络可以反映市场的短期走势变化(相关指标为负相关),且在fast greedy社团划分算法下,加权网络的划分结果与行业分类有明显而稳定的对应关系,可以用于指导在股票市场的分散化投资。
