基于股市网络中心性的投资组合构建与分析

李晨辉 舒子宸 陈俣睿 李双宏 肖雅雯

（1.东方证券股份有限公司系统研发总部 上海 200010）（2.哥伦比亚大学梅尔曼公共卫生学院 纽约 10032）（3.上海交通大学电子信息与电气工程学院 上海 200240）

1 引言

股票市场是一个公认的具有复杂度的系统，通过股市中各股票之间的相关性构建网络，对于研究股市的运行机理有着很好的帮助。国内外许多专家学者将复杂网络的方法应用到股票市场的研究中，通过Pearson相关系数和归一化互信息（normal mutual information，NMI）去衡量各支股票股价波动之间相关程度，并采用相应的网络构造方法，如最小生成树法（Minimum Spanning Tree，MST）［1-5］，最大平面过滤图法（Planar Maximal Filtering Graph，PMFG）［6~7］以及阈值筛选法［8~10］。此外，随机过程以及随机矩阵理论同样被利用与分析股市的相关性中［11~14］。但是，MST生成的网络中包含很少的连边，虽能减少网络的复杂性从而利于分析，但也有可能破坏股市内部结构与关联信息，使得分析结果并不准确，因此不便用于考察股市网络的动态演化情况。近年来，研究者开始改用PMFG和阈值筛选法来进行股票市场网络的研究。相较于MST和PMFG这两种方法，阈值筛选法更为简单易用，但同时也更依赖于研究者的建模经验。根据近几年的研究进展［15~16］，在进行指数构建和策略因子设计时A股市场中度值较大的股票能够取得不错的市场表现。社团划分算法的提出和发展也为对股票市场网络的分析提供了新的方法，其中被广泛应用的有Newman的fast greedy算法［17］，Pascal Pons的walktrap算法［18］和Vincent D.Blondel等的BGLL算法［19］。相关文献已证明以上算法能够有效发现股票市场中的社团结构。Pereira等［20］对不同规模股票市场的复杂网络特性研究中利用BGLL社团划分算法发现H股市场同样具有层次化结构，BGLL已越来越多被用于股票市场动态网络研究。

参考相关研究，本文从选取股票间相关性指标和股票网络构建方法出发，通过比对不同的指标和方法，确定以Pearson相关系数作为衡量股票价格波动间的相关性指标，通过阈值法构建股票市场时序动态网络。随后，构建度中心性策略并进行实证性分析，根据所得结果确定度中心性策略的有效性和策略的优缺点。在此基础上，本文创造性的引入社团挖掘算法来对度中心性策略进行改进，通过实证研究选定挖掘算法，并调整参数，构建了基于社团分析的度中心性策略。本文的主要创新点在于：

1）根据相关分析结果构建了度中心性策略，并且利用社团挖掘算法来对权益组合进行大幅度改进。首先，选用了研究中常用的FN，walktrap和BGLL三种算法进行网络挖掘，并通过Salton，Jaccard，Sorenson和继承比率四个相似性指标，在网络结构分析的同时比对三种挖掘算法的优劣，从中选出最优者用于选股。随后，将动态网络的思想引入到选股的过程当中，通过比较多个时间窗口下的社团挖掘结果，从不同的社团中选取属性相对稳定的大度值股票构建权益组合。实证分析表明，由此改进的度中心性策略能够在保留大度值股票上涨行情跑赢大盘的优点的同时维持波动性的相对稳定，从而可以取得较好的市场表现。

2）本文探讨了不同相关性指标和网络构建方法下的股市网络，通过彼此间的比较，发现了A股市场和美国股市等其他股票市场在网络特性上的不同，并进行了相应的分析论证。

2 基于相关性的A股市场时序动态网络构建

本章分别采用两种相关性的度量Pearson相关系数和NMI去衡量沪深股市中的各支股票价格波动之间相关性并择优，随后通过阈值法以及PMFG算法两种不同的股市网络构建方法尝试构建的中国股市网络，分析其动态演化特性，寻找股市网络与证券市场状况之间的联系，从而找寻一种合适的股市相关性网络建模方法反应真实股市的状况。

2.1 股票数据选取和动态网络相关性指标确定

本文所使用数据来自聚宽（joinQuant）提供的金融数据接口，主要包括日收盘价，包含从2010年1月4日 至2020年2月20日 共计3798支股 票 的日收盘价格。其中，使用2010年1月4日至2016年12月30日共1700个交易日的数据用于选定相关性指标和网络构建方法，剩余部分则进行基于时序动态网络的投资策略的实证性分析。

收益率的计算公式如下：

其中，股票i在t时段的价格（收盘价或均价）为pi(t)，上一个时段的价格（收盘价或均价）为pi(t-Δt)。

设定以100个交易日为时间窗口长度，20个交易日为步长，分别计算不同时间窗口下的Pearson相关系数和NMI，得到股票间的相关系数矩阵，构建两个均有81个时间窗口的加权时序动态网络模型。Pearson相关系数和NMI的均值变化情况如图1所示。

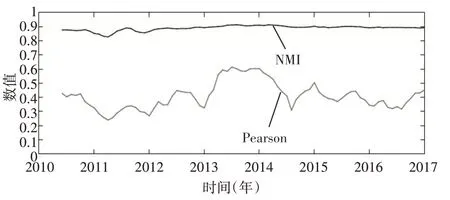
图1 两种相关性指标均值的变化情况

不难看到，相较于Pearson相关系数，NMI的均值较高且波动区间很小，说明NMI均值难以反映股票市场行情走势。进一步分析并观察NMI数值分布的变化情况，如图2所示。

图2 股票价格波动之间归一化互信息分布的变化情况

2010年1月至2016年12月 区间内，NMI分布集中在0.8~1之间且方差较小。结合之前结果，NMI不适合选定为相关性指标用于动态网络分析。究其原因，我国A股市场严格的涨跌停板制度和交易过程中明显的板块效应影响了基于归一化互信息的股市网络的性质［21~22］。因此，依据上述相关性指标性质分析结果，选择Pearson相关系数来描述股票间关系。

2.2 网络构建方法的选定

已有研究［2，6，23~24］中将阈值范围定为Pearson相关系数均值变化区间下界和上界加上一倍标准差之和。考察阈值［0.45，0.70］区间内的网络性质，以0.05为步长择取阈值参数生成网络。当两股票间Pearson相关系数值大于阈值时，则在网络中对应节点间加入连边；否则不加入。所得到的无权动态网络的连边密度变化情况如图3所示。

图3 不同阈值下网络连边密度的变化情况

随着阈值θ的增大，连边密度均值和变化幅度均逐渐变小，并且随时间的动态变化是稳定的，表现在它们的动态曲线具有相近的趋势。为使得生成的时序动态网络随着时间存在明显的变化情况，同时变化幅度不宜过于剧烈，综合考虑选定θ=0.60。

为了考察股市阈值网络拓扑结构的稳定性，引入一个相似性指标，其定义为相邻两个时间窗口的股市网络中共有连边的比例［16］：

其中，Ei为第i个网络的连边集合，|Ei|为其对应的连边数目。两种不同算法所得到网络的相似性指标变动情况分别如图4和图5所示。

图4 阈值法下股市网络相似性指标的变化情况

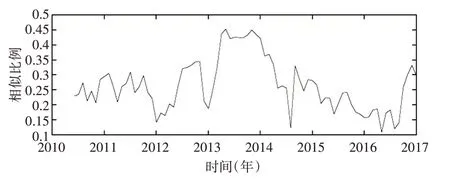
图5 算法下股市网络相似性指标的变化情况

可以看到，阈值法所得到的股市动态网络在相似性指标上明显高于PMFG所得网络。前者相似性指标均值为0.623，而后者的相似性指标均值仅为0.279。这意味着对于PMFG所构建的网络，在2010年1月至2016年12月的区间内，前一时间窗口的连边平均只有27.9%被下一时间窗口所继承。因此，基于PMFG所得网络的连边动态变化剧烈，无法满足能有效反映网络演化过程这一要求。综上所述，选择以Pearson相关系数作为衡量股票价格波动间的相关性指标，通过阈值法构建股票市场时序动态网络。

3 基于度中心性的投资策略实证性分析

在上文所构建的时序动态网络的基础上，引入度中心性投资策略，并进行实证分析。所使用日收盘价数据来自聚宽（joinQuant），共涉及3798支股票，所在时间段为2017年3月8日至2020年2月20日，在剔除了法定节假日等股票市场非交易日后，剩余720个交易日记录。利用Pearson相关系数衡量股票价格波动间相关性，并通过阈值筛选法来构建股票市场时序动态网络。

对于所得网络，依据度中心性来选股构建权益组合。具体方式如下：选取前一时间窗口网络中度值为前20名的股票，按照资金等额分配的原则确定这些股票的仓位，构建权益组合。该权益组合在本时间窗口开始时建立，持有至20个交易日后，即下一时间窗口开始前。由此所得到的投资策略表现如图6所示。

图6 基于度中心性的投资策略的市场表现情况

在同上证综指和沪深300指数走势的比对中，可以发现，基于度中心性策略所构建的权益组合在大多数情况下能够跑赢市场，但也存在如下问题：当整体市场行情向好时，能取得明显高于市场指数的收益；在处于震荡行情时，表现和市场指数相近，并不能取得超额收益；而在处于熊市时，表现较差，跌幅大于市场整体表现。以上的实证性研究表明，在A股市场当中，处于股票市场网络中心位置的大度值节点更容易受到宏观经济和国家政策的影响，在出现利好时，其能够拥有较优的表现，获取超额收益。因而，在市场情绪开始提升或是市场整体估值偏低时，投资具有股市网络的中心节点是不错的选择。更进一步，我们希望通过对度中心性节点进行“分散”，实现风险降低效果。

4 基于社团分析的度中心性策略

4.1 社团挖掘算法的选定

在选定所需的社团挖掘算法的过程中，最为重要的评判标准便是算法能否反映动态网络各时间窗口下对应社团的相似性（继承性）。选取的节点相似性指标有Jaccard指标，Salton指标和Sorenson指标，并将这些指标中所用的对应数据从节点相关扩展至社团相关［15~16］：

在式（3）~（5）中，A1为上一时间窗口（片层）中的社团，A2为本时间窗口（片层）中继承自A1的社团；Γ(A1)为前一时间窗口下社团A1内的节点集合；|Γ(A1)∩Γ(A2)|代表社团A1和A2的交集内节点个数；k(A1)为社团A1内的节点间度值之和。此外，为了更直观的体现所在时间窗口下的社团同所继承的社团之间的节点相似程度，提出继承比率指标：

对于相邻时间窗口（片层）的社团继承关系确定的原则为：对于后一时间窗口内的一个社团，遍历其与前一时间窗口下的所有社团的交集，认为其继承自与其交集内节点数目最大的前一时间窗口下社团。

在这里，我们依旧使用第三部分所得到的网络进行分析和选定，而候选的社团挖掘算法有FN，walktrap和BGLL三种，在每一个时间窗口中，对于社团挖掘算法所得的各个社团分别计算上述四个指标，而后进行加总平均。股票市场网络在不同社团划分算法下片层间相似性指标结果如表1所示。

表1 不同社团划分算法下社团相似性指标均值

不难看到，FN算法所得结果在继承比率和Jaccard这两项指标明显高于另外两种算法，说明不同时间窗口下，社团内节点变化较小；相较之下，walktrap算法在Salton和Sorenson指标上表现优于FN算法，即其在网络拓扑结构上相对稳定。考虑到策略中主要关注社团节点的稳定性，最终选定使用FN算法进行社团划分。

4.2 基于社团分析的度中心性策略的实证性分析

基于社团分析的度中心性策略具体步骤如下：设定动态网络构建时间长度为140个交易日，在该段时间内，以100个交易日为时间窗口长度，20个交易日为步长，得到3个时间窗口，并以此便获得了时序动态网络。在该动态网络中，利用FN算法进行社团挖掘，找寻能够始终位于同一社团的股票，并从不同社团中均匀挑出共20支股票构建权益组合。该权益组合持有20个交易日，直到下一个动态网络给出新的权益组合。对这一改进后的策略进行实证分析，结果如图7所示。

图7 基于社团分析的度中心性策略市场表现情况

可以看到，基于社团分析的度中心性策略整体市场表现要明显优于之前的度中心性策略，相关的市场表现指标可见表2，其中，两种策略的波动率是按照初始价值等于沪深300指数计算的，而计算夏普比率时使用的无风险收益率为rf=2%。

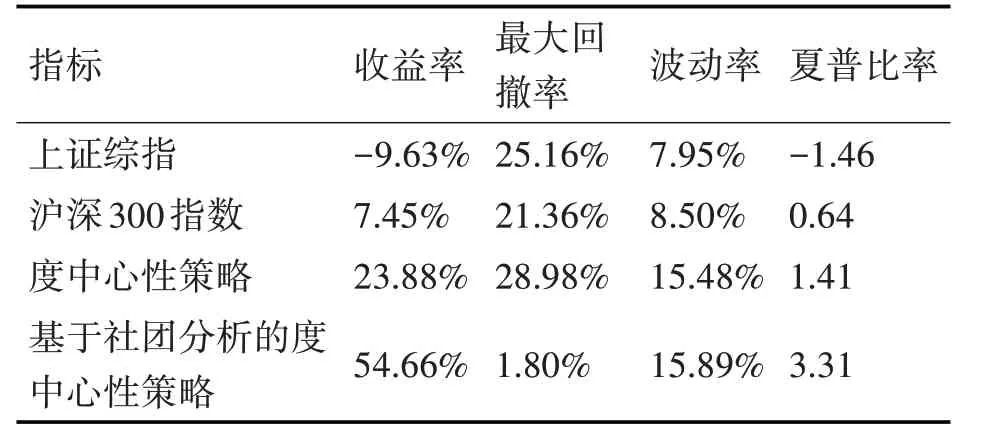
表2 两种不同的度中心性策略市场表现相关指标

尽管基于社团分析的度中心性策略在波动率指标上没有明显的下降，但收益率和最大回撤率的明显改善已经证明了策略的有效性，由此使得夏普比率提高了1.34倍。基于社团分析的度中心性策略把社团挖掘，动态网络和度中心性的思想融合在了一起，在一定程度上实现了分散化的要求，并保留了大度值股票能够跑赢市场的特性，因此取得较好的市场表现。

5 结语

本文分别采用两种相关性度量Pearson相关系数和归一化互信息（NMI）指标衡量沪深股市中各支股票价格波动之间相关性，并通过阈值法以及PMFG算法分别构建股市网络，分析所得股市网络的网络性质的演化过程。通过比较分析，并考虑到我国股市实际情况，选定Pearson相关系数作为股票间相关性指标，并利用阈值法构建时序动态网络，网络的时间窗口长度为100个交易日，步长为20个交易日，阈值为0.60。

在获得股票市场时序动态网络后，参考相关研究，选取度中心性占优的股票构造投资组合，分析表明处于股市网络中心位置的股票可以从利好政策中获取明显超额收益，但波动较为明显，未进行良好的风险分散。为此进行改进，引入动态网络和社团挖掘算法，通过从不同社团中找寻位置稳定且具有大度值的股票构建权益组合。实证研究显示，基于社团分析的度中心性策略的市场表现明显优于之前，可以给出投资者在中国股市中选股的相关建议。