密度峰值自动检测聚类算法*

吴 昊 周建涛 祁瑞东

（内蒙古大学计算机学院 呼和浩特 010021）

1 引言

聚类分析是数据挖掘［1］领域中的一种数据分析方法，它根据数据特征，利用相似性度量规则，将未被预先标记的数据对象相似的数据集归到同一组中。现在，聚类方法已经成为一个重要的研究领域，在互联网［2］、地质［3］和材料学［4］等多个领域都有广泛的应用。为了解决经典聚类算法［5~7］存在参数设置复杂、需要预先输入分类数、无法识别任意形状簇等局限性，2014年Alex与Alessandro在《Science》提出密度峰值聚类算法（CFSFDP）［8］，该算法不需要设置初始簇数量，只需设置一个参数且聚类结果对该参数的选择并不敏感，聚类过程中可以自发地发掘数据集内部结构，并具有非常好的鲁棒性。但密度峰值聚类算法还存在一个问题，初始簇中心的确定需要人工手动选择。

为了弥补密度峰值聚类存在的缺陷，本文基于最小二乘法结合决策图选点提出一种自动选择聚类中心方法，并结合此方法提出自动聚类算法，实验结果表明，该算法可有效地自动识别初始簇中心，并有较好的聚类效果。

2 研究现状与基本知识

2.1 初始簇中心选择

初始簇中心选择的方法大致分为三类，结合其他聚类方法结果两阶段聚类、计算阈值对决策点划分以及寻找区域对决策图划分。结合其他聚类方法两阶段聚类的方法通常要先运行可确定簇数的聚类算法，Sun［9］等使用min-max聚类结果指导密度峰值聚类初始簇的选择，在一定程度上可以找到合适的簇，但时间成本相当高，Zhou［10］等则使用Canopy进行初始簇识别也存在以上问题。阈值计算方法与b-ayes信息准则相类似，迭代计算阈值进行参考簇中心的选择，2019年Sun和Jiang［11］提出使用高斯分布异常点检测思想迭代概率阈值对初始簇进行划分，虽可以较有效地确定簇数，但在计算过程中引入了新的参数需要选择，这淡化了密度峰值聚类算法的优势。寻找区域的方法参照S.Salavador［12］所述Gap检验，通过结合决策图的图像特征计算来找到下降剧烈和平缓之间的分界区域，如2017年Wang［13］等使用点组角度余弦最大值来界定区域。寻找区域的方法往往需要设置少量参数，更适用于对密度峰值聚类算法初始簇的选择，但现有的区域寻找方法计算量较大。本文提出使用拟合直线的方法且对该方法进行优化，并结合新的选点策略提出自动聚类算法，下一小节介绍密度峰值聚类算法的基础知识。

2.2 密度峰值聚类算法

本节介绍密度峰值聚类算法中的一些定义、算法思想和具体算法过程，并分析算法过程中存在的问题。

算法思想基于一个观察：每一个簇中的密度大的区域总被密度小的区域包围。算法的聚类中心满足局部密度较大且离比它局部密度大的点较远。

密度峰值聚类算法首先需要选择初始聚类中心，在簇中心的选择过程中，设数据点i，需要计算局部密度ρi和到密度比自身高的点的距离δi，数据点i的局部密度的计算公式为

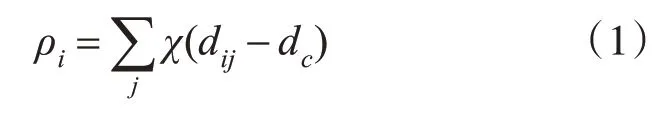
其中，dij为点i到点j的距离，dc为截断距离，χ(x)在当x<0时χ(x)=1其他情况χ(x)=0，局部密度ρi也就等于点i在dc范围内的点的数目。

局部密度较大且δi较大的点将被选为簇中心，δi的计算公式为

在当前计算点为密度最大点时δi=maxj(dij)。选择初始聚类中心的具体步骤需要依照上述密度和距离组成的决策图，通过在决策图中选取离群较远的点。决策图是选择聚类中心的关键，Alex给我们提供的决策图由ρ和δ组成，他同时给出的手动选点方法是尽量选择决策图右上方区域中的离群点，也就是ρ和δ同时显著大的点，但这些点可能仅仅是部分而不是全部的簇中心，如图1。

图1 Iris数据集手动选择决策图

图中右上角两个实心点是非常突出的更容易被人为视作仅有的两个初始簇中心，但Iris数据集正确分类数应为3，可见出现了簇中心少选的情况，而这种情况在手动选择簇中心时是很常见的。找到初始簇中心之后，其他点归于最临近且局部密度最大的簇。对于每个簇都需要一个边界区域来对不同簇进行划分，边界区域（border region）为每个簇的划分界限，每个簇的边界区域由该簇中的点集组成，点集中成员点满足距其他簇中点的距离在dc之内。

不属于该簇且未被划入边界区域的点则为该簇的环（halo），环点则适合选为噪声点。

根据上述算法思想，密度峰值聚类算法的关键步骤如下：

1）输入数据集S的距离矩阵

2）使用式（1）计算每个点的局部密度ρ。

3）使用式（2）计算距离密度较大点的距离δ。

4）根据计算结果构造ρ-δ决策图，选择ρ和δ都明显大于其他点的数据点作为初始簇中心。

5）将簇中心外的数据对象归到距离较近且局部密度大于它的簇。

6）输出数据对象的聚类结果。

3 自动聚类算法

本节将针对密度峰值聚类算法存在的手动选择簇中心的问题，使用最小二乘法结合决策图进行选点自动化。并且，为了提高运算速度，使自动选点更快速，同时使选点策略脱离经验化，使用了新的选点策略。以此又提出密度峰值自动聚类算法ADPCA（A-utomatic Density Peak Clustering Algorithm），在无需人为干预的情况下取得更好的聚类效果。

为了减小计算误差同时便于实现自动选择簇中心，本文在计算局部密度和决策图的使用与上文介绍方法有所不同，局部密度计算使用了高斯核，相比式（1），高斯核计算数据点有相同局部密度的概率较小，从而有效避免冲突；决策图方面使用γ-n决策图。具体公式见式（3）。

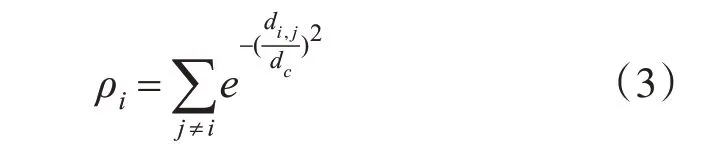
其中di，j表示di和dj之间的距离，dc表示截断距离。γ计算公式见式（4）。

在γ-n决策图中，γ分布曲线特点总体呈单调递减，且在下降过程中存在一个位置，该位置我们称为中间位置，它将图像分为左右两部分，左半部分下降速度快点较为稀疏，右半部分点较为密集下降更平缓。我们想要求得的簇中心特点是局部密度ρi和δi都较大的点，即γ值较大点，也即是要求左半部分的所有点作为簇中心点，由于簇中心点相比于其他点会大很多，那么我们接下来的工作就要寻找中间位置从而找到中间位置左侧曲线上的点作为簇中心，γ-n决策图例如图2所示。

图2 γ-n决策图在Aggregation数据集中使用

本文中我们选择使用两条直线来表示左右两部分区域，并在两直线交点处作为中间位置［11］。拟合直线时我们使用最小二乘法［14］，对于曲线左右两部分分别使用最小二乘法寻找拟合直线，对于每条拟合直线，我们设直线通过计算最小化平方误差和来解得直线，平方误差和如式（5）。

要想求得式（5）的最小值，对式（5）中a和b分别求偏导数，让它们分别等于零。推导后得出正规方程（6）和（7）。

求解得a和b的表达式（8）和（9）。

从而得出左右直线。

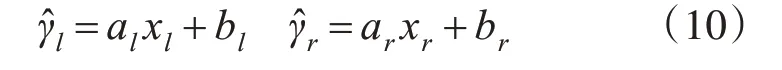
下面的工作我们需要通过式（11）计算每条直线的均方根误差（RMSE）并通过式（12）计算结果求得全局均方根误差，从而在全局均方根误差最小处找到合适的分界点C。其中xl=[2 ，3，…，c]，xr=[c +1，c+2，…，m]。

我们设左直线为L右直线为R，以左直线L（右同理）为例的RMSE计算式（11）：

总的RMSE计算公式为式（12）：

我们要求的目标C为式（13）：

上述过程中由于分界点更容易偏向于左半部分分布，我们不使用所有点进行迭代，从而将有限的计算力集中于最可能出现分界点C的区域，因此我们从x=2开始向x轴正向选m-1个点。因为c是区分是否为簇中心的分界点，我们的选点策略根据这一点首先要计算最可能成为簇中心的点的个数，然后将求得的个数乘以倍数k以覆盖潜在的分界点C，选点策略过程在算法计算ρi和γi时同时完成，选点策略主要步骤如下：

1）计算平均局部密度mp，和δ值的标准差sδ。

2）统计点集

{x|ρ(x)>mp，且δ(x)>1.5sδ}中的点的数量n。

3）当 数 据 集 大 小DT<1000时m=6n，当DT≥1000时m=10n。

策略中第一步与第二步意在找出近似簇中心的点的数量，而在第三步中对可能存在的分界点C进行覆盖，且保证不选择过多的点造成计算压力，同时在实际应用过程中m应小于，N为数据集大小。最终的自动聚类算法关键步骤如下：

1）输入数据集S的距离矩阵；

2）计算数据点i的ρi和γi通过式（3）、（4）；

3）通过γ值构造γ-n决策图；

4）使用选点策略计算m，设RMSEC={}；

5）使用式（8）~（12）迭代计算每个选点处的RMSEC加入到RMSEC向量；

6）使用式（13）计算C的位置；

7）在γ-n决策图中选择[1 ，2，…，C]点作为初始簇中心；

8）分配非簇中心点到最近且ρ较大的簇中；

9）输出簇k的点集a。

算法流程图3所示。

图3 ADPCA算法流程图

4 实验分析

本文实验环境为，3.5GHz CPU，16GB内存，Windows10操作系统下，使用Matlab2020a完成。实验选用6个UCI常用数据集来验证自动密度峰值聚类算法对于聚类工作的有效性，数据集包括二维数据和多维数据，使实验过程尽可能广泛含盖数据的各种分布形式。

具体数据集信息见表1其中数据集都有不同的分布特征。Aggregation数据集有7个类圆形的分布，其中两个类圆形之间有连接部分；Iris是一种常用的多重变量分析的数据集，在统计学和机器学习领域都很常用的数据集，通过它既可测试算法的准确度，也可以检验算法识别噪声的能力；R15是生成用以测试多个聚类数的数据集，它包含15个不同形状的簇；Spiral数据集呈旋涡形状分布，其中组成旋涡的每一条圆弧曲线为同一簇，数据集用以测试不规则曲线形簇是否能准确聚类；Ruspini数据集成四部分较分散分布，用以测试对不规则分布的数据集聚类效果；Sonar数据集用以测试在较高维度情况下的聚类效果。

表1 数据集信息

该算法只需设置一个参数截断距离dc，聚类结果对该参数设置不敏感，此参数的选择时使在每个数据点的截断距离范围内的邻居点数应占数据点总数的2%~3%［8］，本文在实验过程中将此值选择范围定在4%。ADPCA算法在计算距离矩阵、局部密度、较高密度距离时的时间复杂度为O(n2)，选点策略实施包含在上述计算中。类算法必在降序排γ值时的时间复杂度为O(n log(n))，而聚类时的时间复杂度为O(n)，综上ADPCA算法的时间复杂度为O(n2)，而距离矩阵是每个聚须计算的一步，因此如果不考虑参数计算，ADPCA算法在时间复杂度仅为O(n log(n))［15］。

我们使用DBSCAN、K-Means、DPC、ADPCA算法并使用ARI［16］（调兰德指数）对相同数据集聚类结果进行对比分析。

表2所示结果中，DBSCAN想要趋近期望结果，需要不断调整两个参数，可见该算法结果对参数设置的敏感性，如果提供的数据集预先未知期望簇数的情况下想要较为准确的聚类难度较大。K-Means算法需设置初始k值，从表中可以看出聚类效果相比其他三种算法较差，实际实验过程中在识别任意形状的簇时效果较差，如在Spiral旋涡型数据集中，在输入k正确的情况下，存在将不同曲线的点划分到同一簇中的情况。DPC在初始簇数选择正确的情况下对任意形状的数据聚类效果较好，在手动选择初始簇时不可避免会出现多选或少选。ADPCA无需人为干预的情况下即可获得较好的聚类结果，对参数的设置不敏感，参数设置都较为相似情况下也能取得期望的结果。ADPCA算法通过自动寻找初始簇中心进行有效聚类，我们使用UCI常用数据集测试该算法。图4为ADPCA聚类结果，可见不同形状的簇也可以有良好的聚类效果，从图4（a）聚类结果中，可见ADPCA可准确识别任意形状的簇；对于在图4（b）聚类结果中存在的连通点干扰的两个簇也有较好的聚类效果；图4（c）中的螺旋形数据与图4（e）的非规则数据集可准确聚类；图4（d）为ADPCA面对多分类数时的聚类结果表现，综上说明ADPCA可以自动准确地计算簇数，同时可以将每个点正确地分配到任意数据集形状的类中。

表2 聚类算法对相同数据集聚类数对比

图4 ADPCA在UCI常用数据集决策图和聚类结果

从图5中数据分布无特定形状，密度较高的点分配在一个簇中，而黑色数据点被识别为噪声点，可见ADPCA对任意形状数据识别能力和对噪声点的识别能力较强。

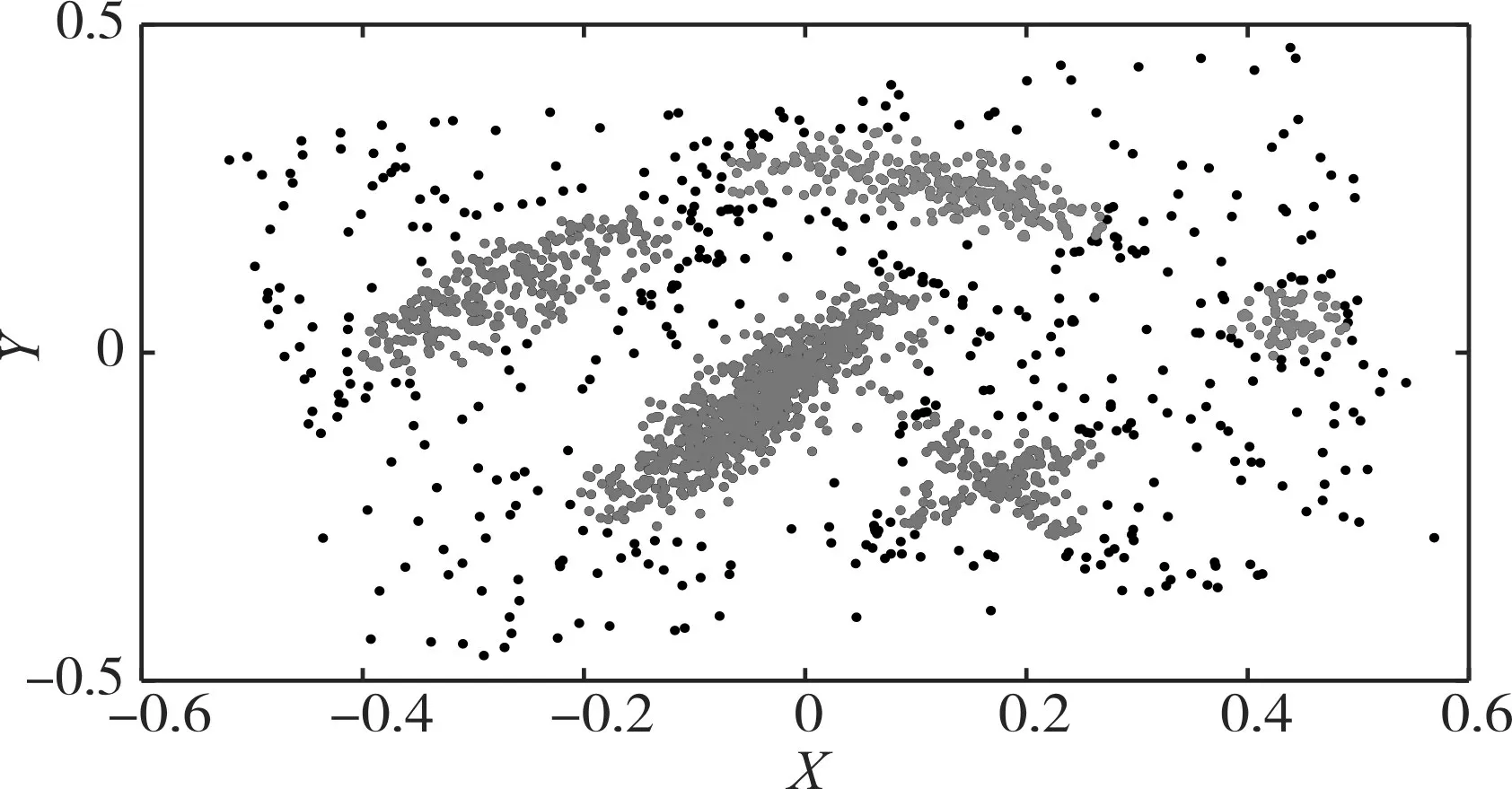
图5 文献［8］数据集聚类结果

5 结语

本文提出了一种自动选择密度峰值聚类算法ADPCA，该算法在聚类过程无需人工参与，能够在聚类前自动识别簇数，无需结合聚类结果分析簇数，同时我们对该算法聚类过程进行优化，提出选点策略减少需要考虑的数据量来减少算法运行时间。为了证明ADPCA算法有效性，我们使用6种UCI数据集进行测试，并测试了在高位数据集下的性能表现，实验结果看来算法的表现良好，在达到有效聚类的同时发现数据集的内部规律，并对噪声点进行识别。

在未来的工作中我们想进一步改进dc选取方法，并解决可能出现的簇中心多选问题，使算法更具鲁棒性。