基于级联加性噪声模型的因果结构学习算法

乔 杰，蔡瑞初，郝志峰

（1.广东工业大学计算机学院，广州 510006；2.佛山科学技术学院数学与大数据学院，广东佛山 528000）

0 概述

因果网络是一种描述多维数据间因果关系的网络［1-3］，在地球系统学［4-5］、生物基因学［6］等领域均具有广泛应用。随机试验是因果关系推断的黄金标准［7］，然而通常存在实现成本高、实际操作困难等问题。因此，如何从观测数据中推断出因果结构是一个重要且具有挑战性的课题。目前，研究人员已提出一系列从数据中发现因果关系的方法［8］，但仅能观测到整个因果结构的部分变量，还有研究人员针对存在隐变量的因果结构学习提出FCI［1］、RFCI［9］、GFCI［10］等算法，然而这类算法具有大量不可识别的因果边。对于某个不存在v-结构［6］的因果对，如果其结果变量无法观测，只能观测到结果变量的子代，那么就存在一条级联式传递的因果关系，而这样的因果关系通常会破坏非线性函数式因果模型的可识别性。CAI 等［11］在2019 年提出级联加性噪声模型（Cascade Additive Noise Model，CANM），该模型在数据服从非线性加性噪声假设下级联结构仍是可识别的，但只能识别两个结点的因果对，无法学习因果结构。本文针对包含隐变量的级联加性噪声模型，结合基于约束的因果骨架学习算法以及级联函数式因果模型，提出一种混合因果结构学习算法。

1 相关工作

从观测数据中学习因果网络主要包括面向时序序列（如格兰杰因果［12］、基于神经网络的联合识别方法［13］等）以及非时序序列两类算法。本文主要针对非时序数据，从非时序观测数据中学习因果网络分为以下两类方法：第一类是基于独立性的方法，包括基于约束［1］、基于评分［14］等方法，此类方法存在无法有效区分马尔科夫等价类的问题［15］，导致无法推断部分因果结构；第二类是基于函数的方法，此类方法通常假设原因变量与结果变量间存在某种特定的函数映射关系，使得结果变量是由相互独立的原因变量与噪声变量经过映射得到的。通过判断该噪声与原因变量的独立性，在某些条件下能够推断出因果关系的方向，将这类可以推断因果方向的模型称为可识别模型，典型的函数式因果模型一般只考虑两个结点的因果对关系，主要包括线性非高斯无环模型

（Linear Non-Gaussian Acyclic Model，LiNGAM）［16-17］、

非线性加性噪声模型（Additive Noise Model，ANM）［18］、后非线性（Post-Nonlinear，PNL）因果模型［19］。

2 基于CANM 的因果结构学习框架

定义因果结构为图G={X，E}，其中，X={X1，X2，…，Xn} 表示n个因果变量结点，E={(i，j)|Xi→Xj}表示结点间的因果边集合，数据集为，样本量大小为m。假设Xi是Xj的父母，若满足直接因果关系则Xi→Xj，假设Xi是Xj的祖先，若存在间接因果边则Xi→Xk→Xj或Xi←Xk←Xj。定义Xi⊥G Xj|S为给定条件集S，Xi与Xj在图G上条件独立。同时，给出因果忠诚性假设［1］、因果充分性假设等常见的基本假设。因果忠诚性假设保证了真实数据分布与因果结构独立的一致性，这一假设使得通过条件独立性进行因果骨架学习成为可能。因果充分性假设保证了任意两个可观测的因果结点不存在一个共同的隐变量父亲根结点，这一假设使得在隐变量下利用级联因果模型进行方向推断成为可能。

本文使用一种典型因果结构［20］来表达隐因果结构网络。简而言之，对于因果路径，若Xi→Xk→Xj且Xk是隐变量，则在典型因果结构上认为Xi→Xj，对于因果路径Xi←Xk→Xj且Xk是隐变量，同时Xk没有任何可观测的父亲或祖先结点，则认为Xi↔Xj，反复迭代直到结构不再变化。在因果充分性假设下，典型因果结构并不存在形如Xi↔Xj的双向边。

本文的目标是学习典型因果结构网络。图1 给出了基于级联非线性加性噪声模型的因果结构学习算法SCANM 框架。该框架分为两个阶段：第一阶段是将输入的观测数据通过因果骨架来学习因果变量间的骨架；第二阶段利用级联非线性加性噪声模型，针对存在隐变量的数据进行因果方向推断。

图1 因果结构学习框架Fig.1 Causal structure learning framework

3 基于CANM 的因果结构学习算法

3.1 因果骨架学习

因果骨架学习的基本流程为：首先初始化一个完全图作为因果结构；其次使用条件独立性检验对独立边进行删边，直到无法再删除边为止。

算法1因果骨架学习

在算法1中有3层关键的循环：第1层循环（第3行）的目的是从小到大遍历不同长度的条件集以测试条件独立性，条件集长度从0 开始，即初始条件集为空集。这么做是因为如果条件越多，那么条件独立性的判断会越不准确，所以倾向于从小到大遍历。第2 层循环（第5 行）的目的是找到每条满足给定条件集的边，此外，对于某条边(Xi，Xj)而言，其条件集应该只会出现在Xi的邻居中，即属于集合Y⊆adj(G，Xi){Xj}，通过该方法可以加快遍历条件集的速度。第3 层循环（第7 行）的目的是遍历所有满足集合长度等于length 的条件集，即|Y|=length，并使用遍历的条件对结点Xi和Xj进行独立性检验，如果发现存在一个条件使得它们独立，则删除这条边。通过以上步骤，可以学习到典型因果骨架图G。

3.2 因果方向推断

通过因果骨架学习找到典型因果骨架后，需要对每条边进行因果定向。由于隐变量的存在且在因果充分性假设下，因此会遇到X→Z→Y和X→Y←Z两类存在隐变量的结构，其中Z均是不可观测的。

3.2.1 结构级联非线性加性噪声模型

对于第1 类结构已在非线性级联加性噪声模型中得到解决。对于第2 类结构，CANM 是没有考虑的，即X→Y←Z*，在此使用Z*加以区分。该结构满足ANM 模型，即Y=f(X，Z*)+ε，且Z*是隐变量。因此，本文认为非线性级联加性噪声模型可以应用于该结构，通过对第1 类结构的边缘分布进行变换使其得到等价于第2 类结构的形式：

其中：nz是在第1 类结构分布下X→Z的噪声，在第2 个等式中使用一般的f表达了中间传递过程，即Y=fy(fz(X)+Nz)=f(X，Nz)。关键在于第3 个等式，如果令噪声分布与Z*的分布相等，则可以得到等价于第2 类结构的边缘分布。换而言之，可以使用CANM框架对第2 类结构进行建模。在下文中将给出CANM 的变分下界以及基于变分自编码机的优化方案。

3.2.2 变分下界

根据式（1）可进一步将单个隐变量推广到多个，并且它们的噪声用向量n表示，因此非线性级联加性噪声模型的边缘似然度可表示如下：

基于式（2）可以给出在样本点(x(i)，y(j))下的边缘似然度的变分下界：

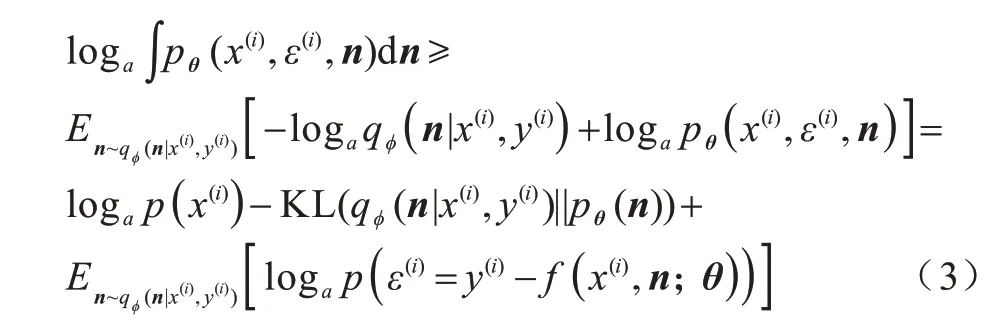
其中：qφ(n|x(i)，y(i))是变分分布的，其作用是近似后验分布pθ(n|x(i)，y(i))，当且仅当KL(qφ(n|x(i)，y(i))||pθ(n|x(i)，y(i)))=0 时，上述下界的等号成立，即只要能够找到一个足够近似的变分分布，就能近似最大化模型的边缘似然度。

3.2.3 变分自编码机

为更好地优化边缘似然度的同时近似后验分布pθ(n|x(i)，y(i))，使用基于变分自编码机（Variational Auto-Encoder，VAE）［21］的求解方案。具体地，使用多层感知机（Multi-Layer Perceptron，MLP）来分别作为编码机qφ(n|x(i)，y(i))和解码器pθ(n|x(i)，y(i))的全局近似器［22］。同时，针对期望项中的梯度求解问题，使用一种重参数化技术，假设先验分布p(n)～N(0，I)服从高斯分布，使得式（3）改写如下：

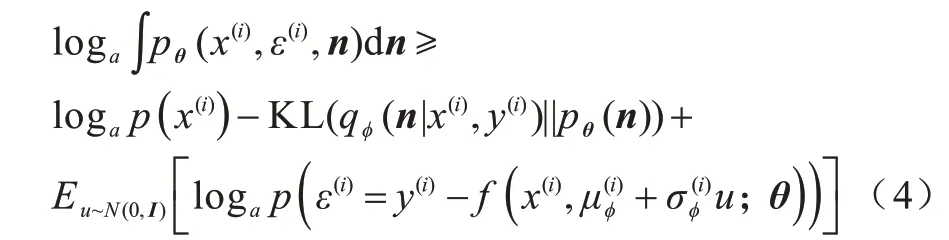
3.3 算法描述

在得到各种隐变量结构下仍然适用的因果方向推断方法后，将这种结构级联非线性加性噪声模型应用到典型因果骨架上，得到一种基于级联非线性加性噪声模型的混合因果结构学习算法。

算法2混合因果结构学习

算法2 分为两个阶段：第一阶段是使用算法1 学习出典型因果骨架（第1 行）；第二阶段是使用级联非线性加性噪声模型对每个因果边进行方向推断（第2～12 行）。最终算法的输出是典型因果结构（第13 行），该结构揭示了变量间存在隐变量下的因果结构关系。

4 实验与结果分析

使用虚拟因果结构与真实结构数据集对模型进行评估，将本文SCANM 算法与以下主流因果结构学习算法进行对比：1）基于盲源分离方法在线性非高斯数据下进行因果结构学习的LiNGAM 算法［16］；2）基于爬山法与贝叶斯评分进行因果结构搜索的HC 算法［23］；3）将约束与贝叶斯评分两者集成进行因果结构搜索的MMHC 算法［24］。为验证隐变量建模的有效性，在因果结构上的每一个因果对之间均会引入额外的隐变量，该隐变量满足级联加性噪声的形式。在实验中，每组参数都至少运行80 次以上，并采用F1 值（F）作为评价指标，计算公式如下：

4.1 虚拟因果结构数据集实验

在虚拟因果结构数据集中设计4 个变量控制实验，每个实验都会随机生成不同的虚拟因果结构，具体设置为：隐变量数量为0、1、2、3、4，结构维度为6、10、15、20，平均入度为1.0、1.5、2.0，样本数量为250、500、1 000、2 000、3 000、4 000、5 000，其中加粗数据表示在各控制实验中的默认设置。

图2 给出了不同隐变量数量下的实验结果。由图2 可以看出：一方面，SCANM 算法在0 个和1 个隐变量下F1 值都在0.87 附近，验证了隐变量实验的有效性；另一方面，随着隐变量数量的增加，在隐变量数量为4 时，SCANM 算法的F1 值下降至0.73，这是因为隐变量的增加会导致信噪比的降低，从而影响模型学习效果。

图2 不同隐变量数量下的实验结果Fig.2 Experimental results under different number of hidden variables

图3 给出了不同结构维度下的实验结果，可以看出在不同的结构维度下SCANM 算法的F1 值在0.83 附近波动，这意味着级联非线性加性噪声模型在不同的结构维度下具有较强的鲁棒性。

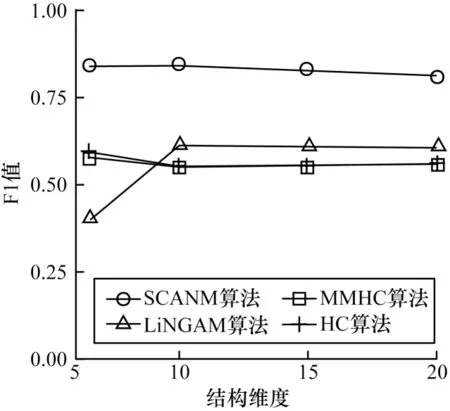
图3 不同结构维度下的实验结果Fig.3 Experimental results under different structural dimensions

图4 给出了不同平均入度下的实验结果。由图4 可以看出，HC 与MMHC 算法对平均入度较为敏感，而且随着平均入度的增加F1 值下降比较明显，尤其在平均入度在1.0～1.5 时，F1 值下降了近0.1，其原因是当边数较多时，若算法无法识别存在的隐变量，则出错的边数会增多，从而使得F1 值下降，而SCANM 算法由于对于隐变量的方向也可识别，因此对平均入度不敏感。

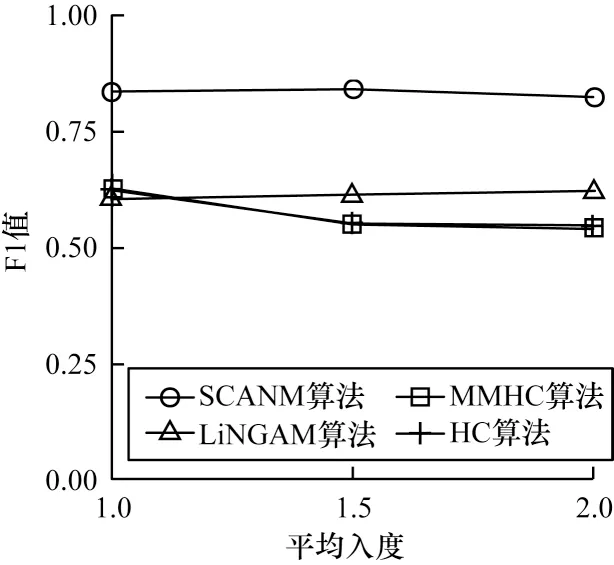
图4 不同平均入度下的实验结果Fig.4 Experimental results under different average in-degree

图5 给出了不同样本数量下的实验结果。由图5可以看出，所有算法对于样本数量都较为敏感，样本数量是一个较为重要的变量。尽管在样本数量较少时，所有算法的F1 值均不太理想，但SCANM 算法的F1 值仍至少比其他算法高0.15，体现出其性能的优越性。

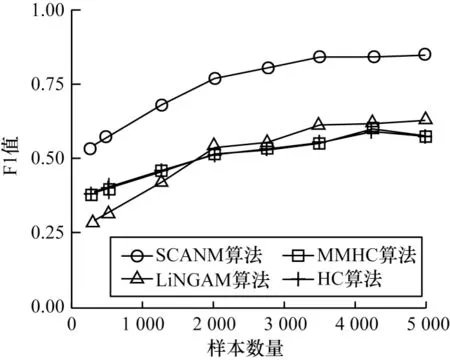
图5 不同样本数量下的实验结果Fig.5 Experimental results under different number of samples

4.2 真实因果结构数据集实验

选择4 种真实结构进行测试，真实结构数据来自https：//www.bnlearn.com/bnrepository/，具体信息如表1所示。

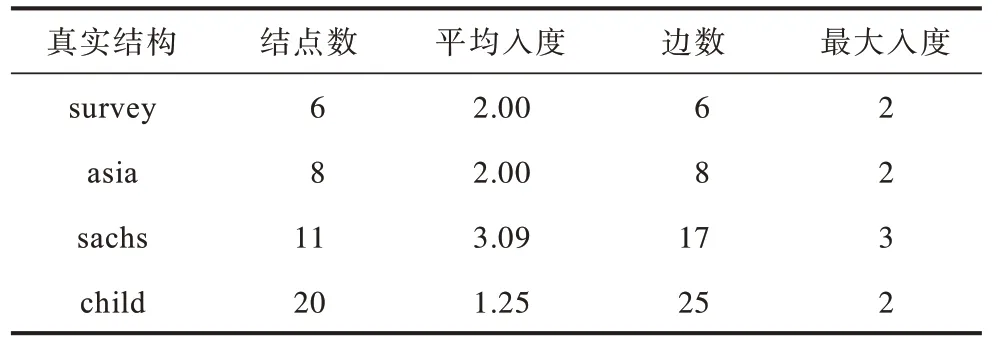
表1 真实因果结构数据集信息Table 1 Real causal structure dataset information

在真实因果结构数据集实验中使用F1 值、准确率、召回率作为评价指标，计算公式如下：

在真实因果结构数据集中，使用与虚拟因果结构数据集实验相同的设置，实验结果如图6～图8 所示，总体而言，SCANM 算法在不同真实结构的平均F1 值为0.82，相比其他算法提升了51%。特别地，可以看出：在不同的真实结构中SCANM 算法均取得了最好的效果，尤其在sachs 结构中，其原因是sachs 结构的平均入度更大，级联非线性加性噪声模型在该情况下具有更好的效果；对比算法在不同的真实结构中召回率偏高而准确率偏低，尤其在child 结构中最为明显，主要原因为没有考虑隐变量的存在，容易学习出冗余边。上述结果验证了SCANM 算法的有效性。

图6 真实因果结构数据集中的算法F1 值比较Fig.6 Comparison of F1 values for algorithms in real causal structure dataset

图7 真实因果结构数据集中的算法准确率比较Fig.7 Comparison of precision for algorithms in real causal structure dataset

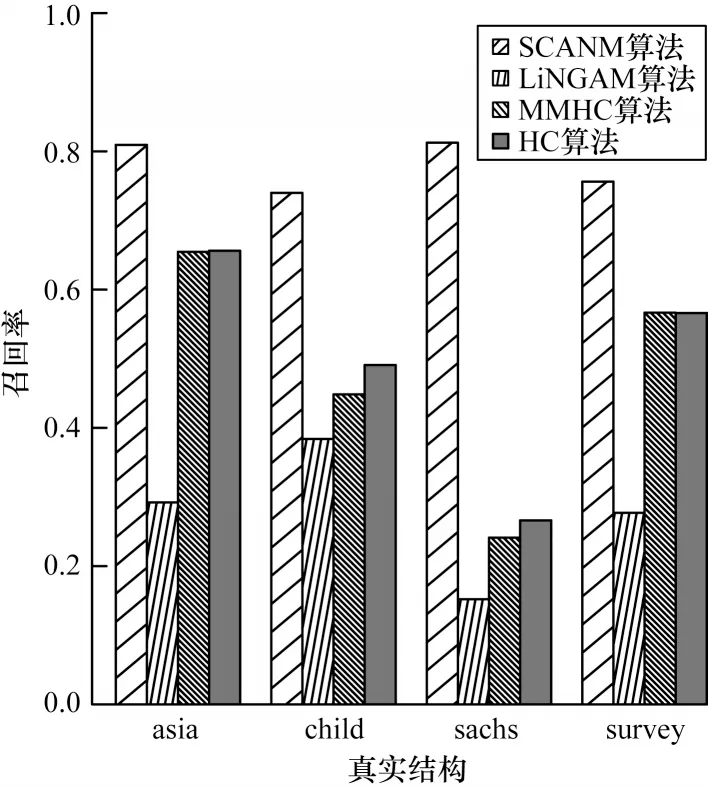
图8 真实因果结构数据集中的算法召回率比较Fig.8 Comparison of recall for algorithms in real causal structure dataset

5 结束语

本文提出一种基于结构级联非线性加性噪声模型的因果结构学习算法，通过联合传统基于独立性的因果骨架学习算法以及级联加性噪声模型，解决了存在隐变量的因果结构学习问题。实验结果表明，在虚拟结构数据集和真实结构数据集下，该算法相比主流因果结构学习算法准确率更高、鲁棒性更强。后续将研究不满足因果充分性假设下的因果结构学习算法，进一步扩展级联非线性加性噪声模型的适用范围。