基于径向曲线与支持向量回归的颅骨修复方法

陈仲晗，赵俊莉，黄瑞坤

（青岛大学数据科学与软件工程学院，山东青岛 266071）

0 概述

颅面复原是根据颅骨和面皮之间的形态学特征建立一一对应关系，从而可以依据未知颅骨生成对应的面貌。完整的颅骨能更好地复原出人脸，如果颅骨上有洞或者较大的缺损就很难准确地复原人脸。考古学和刑侦学等领域在研究颅面工作时，针对缺损颅骨，在复原面貌之前要对有缺失的颅骨进行修复。现有孔洞修复技术［1-2］采用数字几何的方法对孔洞进行修复，但补洞效率和准确性还有待提高。

孔洞修复法主要包含体数据修复法和三角网格修复法。基于体数据方法是将待修补颅骨模型转化成体网格的形式，在体空间中定位到孔洞及其孔洞周边区域，建立孔洞和周边曲面函数关系，从而实现孔洞区域修复。DAVIS 等［3］建立孔洞与周围区域之间的空间函数关系，根据对应关系利用体素扩散算法实现孔洞的修复，但该方法在修复过程中耗时较长。NOORUDDIN 等［4］将待修补的孔洞转换为体模型，通过体表示提取连续的曲面，从而进行孔洞修复，该方法能够处理比较简单的孔洞，但复杂孔洞难以修补。JU 等［5］利用八叉栅格对复杂的孔洞进行修复，该方法可以保持特征不丢失，但对于尖锐的地方不敏感。CENTIN 等［6］使用泊松重建方法得到一个隐式函数，然后利用插值的方法对缺失部分复原，复原效果较好，但算法时间复杂度较高。LIN 等［7］提出恢复特征曲线或拐点处缺失点的新型孔洞修补方法，提取边界点和特征点后，使用张量投票来修复孔洞，该方法可有效地恢复尖锐的孔洞。体数据修复法能够较好地处理多种孔洞，但时间复杂度高，在有些情况下修复后颅骨的拓扑结构会出现问题。

基于三角网格的修复方法是直接在待修补三维颅骨模型中进行补洞操作，首先定位到孔洞的周边区域，根据孔洞的边界边和边界点的特征规律，从而在孔洞中插入三角网格。LIRPA 等［8］将网格中的孔洞采用三角网格化方式处理，然后使用光顺等步骤移动和改变点位置，使复原精度进一步提高，但对复杂的孔洞很难直接进行修补，因此JUN 等［9］提出将复杂孔洞转化为相对简单的孔洞进行修补，能够修补复杂孔洞。该方法有时会忽略孔洞周围的网格形态，导致修补结果并不理想。ZHAO 等［10］首先采用波前法和泊松方程对新增顶点进行未知调整，该方法在调整较大位置时会导致修补精度不高。LI等［11］提出基于泊松方程的修复法，对模型曲面全局拟合，调整曲面与孔洞最大化拟合从而实现孔洞修补，但该方法对缺失较大区域修复不理想。WANG 等［12］运用系统灰度预测的方法对缺失洞进行修复，但该方法不稳定，会出现预测错误的情况。QUINSAT 等［13］提出网格变形的方法来填充数字化孔洞，通过最小化网格的变形能量进行实验，能够较好地修复复杂形状。WU 等［14］提出使用边界法向量与误差度量相结合的网格修复法，但对显著特征信息的模型修复效果差。WEN 等［15］在三维网格修复过程中提出自动识别孔洞方法，其在修复过程中忽略了缺失区域存在复杂拓扑结构的情况，且算法的时间复杂度也较高。网格修复法可以较好地保留待修复数据的几何特征，能够保证不改变原有的网格信息，但该方法无法保证修复结果的好坏。

以上两种修补方法对简单孔洞恢复较好，但对于复杂的孔洞区域修补结果较差。虽然当前可收集大量的三维模型建立模型库，并通过合并等方法进行修复孔洞，但需要手工选择特征点，这导致修复的方法效率低。基于样例的复原方式能对较大缺失进行修复，为更好地复原待修复颅骨，耿等［16］提出多样例的三维缺失颅骨的修复方法，在三维颅骨库中寻找一个或多个与待修复模型相似的完整三维模型作为样例，对待修复模型进行分割拼接和融合即可完成修复，但此过程需要选择足够多的样例。

目前改进的修复方法需建立颅骨数据库寻找与待修复模型相似的颅骨模型，同时手动标定特征点，然后进行平移旋转等操作，效率较低。在颅面复原统计模型中，基于回归的方法［17］已经取得了显著的复原效果，而且为应对颅面［18-19］数据点数多、运算量大的特点，研究人员提出颅面的曲线表示方法［20-22］，提高了复原过程的效率，因此将基于曲线的回归方法应用在颅骨修复领域，提高颅骨修复效果。本文通过提取颅骨径向曲线数据进行训练，采用基于非线性回归最小二乘支持向量回归方法，寻找待修复模型中已有数据与缺失数据之间的函数关系，将复原出的孔洞径向曲线与待修复模型中的已有数据进行合并，从而基于统计模型复原出完整颅骨。

1 径向曲线与支持向量回归的颅骨修复模型

从颅骨上提取径向曲线，采用径向曲线上的点表示颅骨的形状，避免人工从颅骨上标定特征点带来的误差，同时也提高了效率。本文将提取的完整颅骨的径向曲线分成两个部分：待修复数据和已有数据。将这两部分数据作为训练样本送入回归模型中，计算出待修复数据和已有数据之间的映射关系，然后根据待修复颅骨径向曲线复原出缺失径向曲线，最后将待修复颅骨径向曲线和生成的缺失数据径向曲线合并后送入颅骨统计模型，估计出待修复颅骨。颅骨修复模型过程如图1 所示。

图1 颅骨修复模型过程Fig.1 Skull repair model process

1.1 径向曲线提取

颅骨径向曲线根据颅骨对称面和颅骨曲面的交点确定，用颅骨径向曲线表示颅骨。颅骨径向曲线提取方式和人脸径向曲线［23］提取方式相同，但重点要解决颅骨上经过洞时径向曲线的提取方法。

1.1.1 颅骨洞

完整的颅骨所具备的洞的个数如图2 所示，主要由鼻洞、左右眼洞、左右耳洞、左右颌骨洞和一个背面洞组成，共8 个洞。由于颅骨的径向曲线是颅骨对称面绕轴线与颅骨三角网格之间的交点，完整颅骨洞内无三角网格，即不能在洞内提取径向曲线，因此在提取颅骨径向曲线时需要定位这8 个洞的边界，从而定位到所属的洞。

图2 完整颅骨图Fig.2 Complete skull diagram

颅骨模型由大量的三角网格构成，在寻找孔洞边界时，需要依次输入三角网格点进行孔洞边界边搜索。除孔洞的边界三角网格外，其他每个三角网格的边都是两个三角网格的公共边，但孔洞边界每个三角网格都有一条边只属于一个三角网格。

在所有的颅骨中查找边界点，以此循环找到所有的边界点和边界边。将这些边界边保存起来，从第一个保存的边界边开始（以图3 中的CD边为例），在所有的边界边中找上一边界边的末点（即含D的边界边），依次类推，直到最后找到一个边界边的末点是第一个边界边的第一个点（即C点）为止，即为第1 个洞。再根据洞的坐标关系，从而确定洞的位置。

图3 孔洞三角网格Fig.3 Triangular grid of holes

1.1.2 颅骨对称面估计

在提取径向曲线时需要估计颅骨对称面，参考文献［24］的方法，采用坐标系平面YOZ选取为镜像平面，对称面和平面YOZ 平行，三维颅骨模型中的颅骨数据关于镜像平面对称，颅骨数据中有N对对称点，根据对称点采用最小二乘拟合的方法求取颅骨的对称面。

通过颅骨对称面与颅骨的三角网格模型的交点计算径向曲线，将颅骨对称面绕轴线以鼻洞上y值最大的点为旋转点逐次旋转（m为径向曲线的条数），对称面每旋转θ度角后与颅骨三角网格的交点就是求取的其中一条径向曲线。

在提取径向曲线后，对曲线中的点数进行了重采样，实验中每条径向曲线的点数取200 个，提取30 条径向曲线，即每套颅骨曲线上共有均匀采样点6 000 个。提取的完整颅骨径向曲线如图4 所示，其中最左边是左侧面，中间是正面，最右边是右侧面对应的径向曲线。

图4 完整颅骨径向曲线Fig.4 Radial curve of complete skull

1.2 支持向量回归

本文采用最小二乘支持向量回归（LSSVR）［25］方法找到以最小偏差，来表示颅骨待修复径向曲线和已有径向曲线间关系的平滑函数，即：

其中：xi(1≤i≤n)表示已有径向曲线；yi(1≤i≤n)表示修复径向曲线。

支持向量回归的目的是找最适合的ω来保证可以表示颅骨已有径向曲线和待修复径向曲线之间的函数关系，则需求解：

其中：ε表示函数的偏差。下面引进松弛变量来允许更多的误差，称为损失函数。所以，可以将式（2）、式（3）写成以下形式：

其中：常数C>0 决定了函数对偏差的容忍度，即模型可以忍受的平滑度和偏差度。通过拉格朗日乘数法得到ω，即：

在式（6）中，αi、是拉格朗日乘数，有：

通 过Karush-Kuhn-Tucker（KKT）［26-27］最优化条件和上面求得的ω可以求得b：

1.3 最小二乘支持向量回归

LSSVR 回归在支持向量回归的基础上可以写成如下优化问题：

其中：C表示正则化参数；ξi是松弛变量。利用拉格朗日函数解这个优化问题，得到如下形式：

1.3.1 基于LSSVR 的颅骨修复

LSSVR 用来找到颅骨待修复径向曲线和已有径向曲线之间的关系。在实验阶段，训练集和测试集套数分别为160 套和30 套。在复原阶段，将一个待修复颅骨径向曲线作为输入数据，并且利用训练得到的映射复原出缺失部分的径向曲线。具体步骤如下：

步骤1将训练样本中待修复颅骨径向曲线数据表示为xi；颅骨已有径向曲线数据表示为yi。

步骤2利用主成分分析（Principal Component Analysis，PCA）法得到的矩阵Ux、Uy，并且将每一个样本都由PCA 矩阵表示，例 如所以，新的测试待修复颅骨径向曲线则表示为

步 骤3根 据LSSVR 算法得到和′间的映射。根据映射关系，可将待修复颅骨径向曲线测试集的缺失径向曲线重构出来。具体步骤如下：

1）确定LSSVR 函数的两个参数：正则化参数和RBF 核函数的参数；

步骤4将复原缺失部分的径向曲线和待修复颅骨径向曲线进行合并，得到合并后的颅骨径向曲线。待修复颅骨径向曲线复原出的缺失部分径向曲线的生成图和合并图如图5 所示，其中，图5（a）是待修复颅骨的径向曲线，图5（b）是恢复的径向曲线，图5（c）是合并后完整的径向曲线。

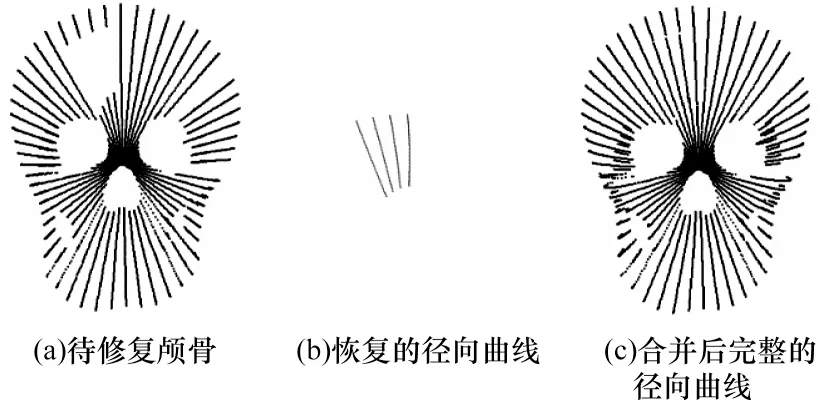
图5 合并后的径向曲线Fig.5 Combined radial curves

1.3.2 基于合并颅骨径向曲线估计待修复颅骨

将图5 中的合并颅骨径向曲线恢复三维颅骨模型需要经历以下2 个过程：

1）颅骨统计模型的建立

2）模型系数α的确定

确定模型系数需要使||S(α)-S*||的结果最小（S*是根据合并径向曲线得出的颅骨模型），即求min||S(α)-S*||。为 求S(α)、S*的最小值，本文使用ICP 算法确定颅骨模型S(α)与复原出的径向曲线Yc（Yc为已有的径向曲线与复原的修复部分径向曲线合并后的径向曲线）的对应点Y′，然后根据Y′-Yc=hyα求解α，其中hy是径向曲线点的对应分量，那么通过可以计算出α系数，多次迭代求最小值时的α。得到确定的模型系数α后，代入颅骨模型进行更新，从而得到待修复颅骨的颅骨模型S(α)。

2 实验结果与分析

本文颅骨数据来自北京师范大学虚拟现实应用教育部工程研究中心创建的颅面CT 扫描数据库，提供数据志愿者年龄最小为19 岁，最大为75 岁。实验中用到190 套颅骨数据，对160 套颅骨数据提取径向曲线，同时将160 套颅骨径向曲线分为颅骨已有径向曲线和待修复颅骨径向曲线，将它们作为模型的训练样本，然后将30 套有缺损的颅骨径向曲线作为测试样本。将复原出测试颅骨缺失部分径向曲线与待修复径向曲线合并，从而复原出修复的颅骨。

2.1 不同核函数与参数核函数的颅骨修复精度对比

2.1.1 线性核函数与高斯径向基核函数的对比

LSSVR 中不同的核函数对实验的影响也不同，算法需要对核函数进行选择，本文实验使用线性核函数和高斯径向基函数（RBF）2 个核函数进行实验，同时将2 种方法生成结果进行误差对比，如表1 所示，将2 种核函数对应生成的修复颅骨与原始颅骨之间采用平均欧式距离计算误差，同样从最小距离误差、平均距离误差、最大距离误差和方差4 个指标比较修复颅骨与原始颅骨之间的精度，表1 最后一行Diff代表不同核函数之间的误差，4 个指标中的均值这一列可以较为明显地观察出RBF函数生成的误差小，同样在最大值和方差这2个指标中也能观察出RBF 的误差较小，第1 列最小值线性较小。

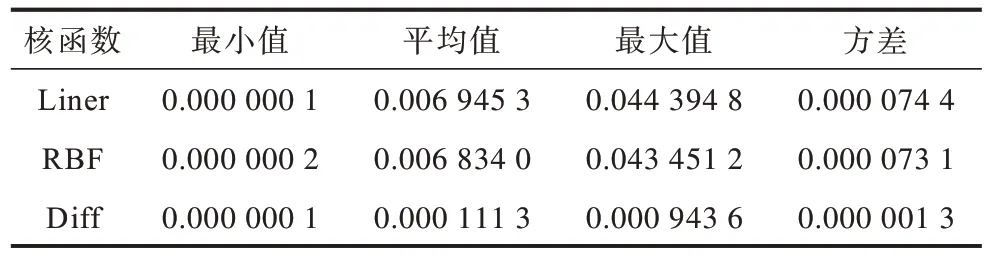
表1 线性核函数与RBF 核函数误差对比Table1 Error comparison between linear kernel function and RBF kernel function

2.1.2 RBF 核函数不同参数误差的对比

通过2 种核函数的最小距离误差、平均距离误差、最大距离误差和方差4 个指标可以比较出RBF核函数生成的修复颅骨的误差更小。RBF 核函数有正则化系数与RBF 核函数系数，调整这2 个系数可以改变误差。最小值、平均值、最大值、方差对比如图6～图9 所示。

图6 不同参数最小值距离误差比较Fig.6 Comparison of minimum values distance error of different parameters

图7 不同参数平均值距离误差比较Fig.7 Comparison of average values distance error of different parameters

图8 不同参数最大值距离误差比较Fig.8 Comparison of maximum values distance error of different parameters

图9 不同参数方差比较Fig.9 Comparison of variance of different parameters

在图6～图9 中，曲线RBF1000 代表正则化参数设置为1 000，RBF 核函数参数为100，曲线RBF20 代表正则化参数设置为20，RBF 核函数参数为100。通过折线图可以看出，在曲线RBF20时的曲线较低，说明RBF20选择的参数效果更好，此参数取值是多次实验取得的结果。

2.2 基于径向曲线的LSSVR模型颅骨修复精度对比

取上面实验得出的最优参数，即LSSVR 函数的正则化参数设置为20，RBF核参数设置为100进行实验。本文采用4 种方法对颅骨修复精度进行对比，分别是基于径向曲线的PCA［28］颅骨修复方法、基于径向曲线的偏最小二乘回归（PLSR）［17］颅骨修复方法、基于径向曲线的最小二乘回归［26］（Least Squares Regression，LSR）颅骨修复方法和基于径向曲线的LSSVR 颅骨修复方法。4 种方法生成的修复颅骨与原始颅骨的平均欧式距离作为修复颅骨与原始颅骨之间的误差，对这4 种方法分别从最小距离误差、平均距离误差、最大距离误差和方差4 个指标比较修复颅骨与原始颅骨之间的精度，对比结果如表2～表4 所示，表中Diff 代表两者之间提高的精度，对应于两种方法的差值。

从表2 数据可以看出，LSSVR 方法的平均误差达到6.834×10-3，比PCA 方法降低了2.90 倍，基于LSSVR方法优于PCA 的方法。表3和表4分别是基于PLSR 方法和基于LSR 方法与LSSVR 方法的误差对比。从表3和表4 数据可以看出，虽然3 种方法产生的差别不大，但是通过4 个指标的误差值可以看出基于LSSVR 方法的误差更小，所以基于LSSVR方法也优于PLSR和LSR的方法。

表2 基于PCA 和LSSVR 方法误差对比Table 2 Error comparison based on PCA and LSSVR methods

表3 基于PLSR 和LSSVR 方法误差对比Table 3 Error comparison based on PLSR and LSSVR methods

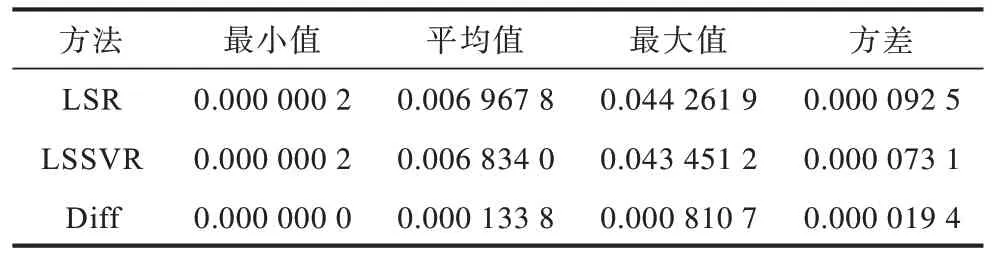
表4 基于LSR 和LSSVR 方法误差对比Table 4 Error comparison based on LSR and LSSVR methods

将4 种方法对颅骨进行修复的效果图与原始完整颅骨进行比较，如图10 所示，其中，图10（a）是样本的源颅骨样本，图10（b）是基于PCA 方法修复后的效果，图10（c）是基于LSR 方法修复后的效果，图10（d）是基于PLSR 方法修复后的效果，图10（e）是基于LSSVR 方法修复后的效果，图10（f）～图10（i）分别是PCA、LSR、PLSR 及LSSVR4 种方法修复后的效果图与源颅骨之间的误差。误差图中的颜色代表修复后的颅骨与源颅骨间的误差大小，其中蓝色表示误差较小，红色表示误差较大（彩图效果见《计算机工程》官网HTML 版）。

图10 4 种方法的效果图和误差图Fig.10 Effect diagrams and error diagrams of four methods

通过图10 可以看出，基于PCA 方法生成洞的误差图中洞区域红色较多，说明PCA 生成的颅骨效果图很差，表示恢复颅骨不理想。观察LSR、PLSR 和LSSVR 方法生成的误差图，可以看出LSSVR 方法的误差图中蓝色区域要多一些，基于LSR、PLSR 和LSSVR 方法生成的效果图和误差图比PCA 方法生成的好，所以基于LSSVR 方法修复颅骨洞更好。通过表2～表4 和图10 可以看出，基于径向曲线与LSSVR 的颅骨修复效果更好。

综上，基于LSSVR 方法的生成效果优于LSR 方法、PLSR 方法和PCA 方法的生成效果。

3 结束语

本文提出基于径向曲线与最小二乘支持向量回归的颅骨修复方法，采用径向曲线表示颅骨特征，同时结合最小二乘支持向量回归方法构建颅骨修复模型，将提取出的颅骨径向曲线分为已有径向曲线和待修复径向曲线，同时将这2个部分作为训练样本，并使用LSSVR统计模型复原出缺失部分径向曲线，然后将待修复径向曲线和复原出缺失部分径向曲线进行合并，最后通过迭代最近点算法将合并颅骨径向曲线与颅骨统计模型进行匹配生成完整的颅骨。实验结果表明，本文方法平均误差达到6.834×10-3，比PCA 方法降低2.90 倍，生成结果优于PLSR 和PCA 方法。本文采用径向曲线表示颅骨曲面，仍属于人工提取特征的方法，下一步将根据深度学习的特征提取能力，自动学习颅骨特征，修复颅骨孔洞。