电场和温度对三角势量子点中极化子基态性质的影响

李志新，张 星，杨名超

(河北科技师范学院物理系，河北，秦皇岛，066004)

量子点中的电子结构并不是像分子或者体材料那样是一个简单的内部极化，对于半导体量子点，量子限制本质上导致了离散能级结构。由于量子点的尺寸分布和形状变化，光谱的不均匀带宽掩盖了其能量状态下的精细结构。随着量子光学器件的广泛应用，发现许多新的效应，而温度对极化子效应的影响已成为低维量子系统中的研究热点。特别是在量子系统中，量子限制增强了电子-声子相互作用。因此，人们对低维量子点系统进行了大量的理论和实验研究[1～3]。同时，随着量子信息和量子计算的发展，许多研究者通过各种理论方法对量子点的性质进行了深入的研究[4～6]。这些研究主要集中在量子点中极化子的性质[7～10]。Sun等[11]利用Pekar类型的变分方法从理论上研究了CsI量子Pseudodot中电场和温度对强耦合极化子第一激发态能量的影响。Sun等[12]利用Pekar类型变分方法、量子统计理论和费米黄金法则，研究了磁场和温度对RbCl抛物型量子点消相干时间的影响，结果表明，极化子消相干时间随着温度的增大而减小。通过求解薛定谔方程的方法，Khordad等[13]研究了GaAs双环类型量子点中热动力学的性质。在外加磁场和电场的情况下，Xiao[14]通过使用Pekar类型的变分方法和量子统计理论，系统的研究了温度对类氢杂质中强耦合RbCl量子Pseudodot极化子基态能量的影响。Khordad[15]利用Lee-Low-Pines幺正变换方法研究了Rashba效应对量子Pseudodot中受限极化子基态能量的影响。Yu等[16]使用Pekar类型的变分方法系统的研究了抛物型量子点中极化子的基态跃迁性质，研究发现极化子基态寿命随着极化子基态能量的增大而增大，随着电子-声子耦合强度、温度和量子点受限长度的增大而减小。额尔敦朝鲁等[17]基于LLP幺正变换，采用Pekar型变分法得到了二维量子点中双极化子的基态和第一激发态的能量和波函数，进而构造了一个双极化子的量子比特。Cai等[18]利用Lee-Low-Pines幺正变换方法讨论了温度对RbCl抛物型量子点中磁极化子基态能量的影响。Tiotsop等[19]利用Lee-Low-Pines-Huybrechts变分技术，三角形束缚势和库仑受限势对极化子基态和第一激发态本征能级的影响。Han[20]通过使用Lee-Low-Pines-Huybrechts变分方法计算了外磁场、体纵光学声子和量子盘厚度对电子-LO声子强耦合磁极化子和量子比特的影响。刘佳丽[21]和米广龙等[22]采用LLP幺正变换、线性组合算符和变分相结合的方法，分别对不同基底上单层黑磷烯中束缚极化子的基态性质和有限深势阱中球型量子点中极化子的基态性质进行了深入研究，然而，采用Pekar类型变分方法研究外加电场下温度对极化子基态能量的影响的研究非常少。为此，笔者拟采用Pekar类型变分方法探讨电场、量子点的受限长度、温度参量、三角势极角对三角形量子点中强耦合极化子基态能量的影响。主要探讨了量子点的电子性质随外加电场、温度和受限长度的变化，期望为新材料和功能量子器件的设计提供理论依据。

1 理论模型与计算

考虑电子在z方向上比在x和y方向受限更强，电子被受限在xy平面上运动。假设量子点中的受限势为三角形束缚势

(1)

式中m*是电子的有效质量，ρ为电子在xy平面上的坐标，ω0和θ分别是量子点受限强度和角参量。在有效质量近似下，沿x方向外加电场的情况下，电子-LO光学声子系统的哈密顿量为

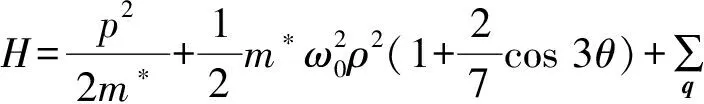
(2)

(3)

上式中

(4)

(5)

这里α是电子-LO体纵光学声子耦合常数。对方程(3)引进Lee-Low-Pines变换，得到

(6)

上式中fq为变分参量，方程(6)代入方程(3)，得到

H′=U-1HU

(7)

假设高斯波函数对基态波函数一直是有效的，电子-LO体纵光学声子系统的波函数被选择为

(8)

(9)

(10)

2 结果与分析

为了更清楚的说明三角势量子点基态能量对量子点受限长度、三角势角参数、外加电场强度和温度参数的依赖关系，进行了数值模拟计算。结果表明，在α=6,γ=0.01，和θ=20°时，对于不同的电场强度F=10,15,20情况下，三角势量子点中极化子基态能量E0随着量子点受限长度l0的增大而减小(图1)。这是因为受限势限制了电子的运动，当受限势减小(ω0降低)时，三角势对电子的束缚减弱，导致极化子能量降低。此外，随着量子点受限长度的减小，量子点受限长度l0对基态能量E0的影响是非常显著的，然而，随着量子点受限长度的增大，电场强度对基态能量的影响逐渐变大，这说明随着三角势束缚的减弱，外电场的影响增强。

图1 不同电场强度下，量子点受限长度l0与 图2 不同温度参数下，量子点受限长度l0与极化子基态能量E0的变化关系曲线 极化子基态能量E0的变化关系曲线

在α=6,F=10和θ=20°，对于不同的温度参数γ=0.01,0.03,0.09时，极化子基态能量E0与受限长度l0之间的变化关系(图2)。结果发现，极化子基态能量E0随量子点受限长度l0的增大而减小。其原因与图(1)相同，同时发现当受限长度足够大时，其影响愈来愈小，最后趋于不变。另外，还发现当量子点受限长度l0保持不变时，极化子基态能量E0随着温度参数γ的减小而增大，这是因为温度升高，更多的声子被激发，声子系的能量增大，进而导致基态能量增大。特别是受限长度足够大时，温度起主要作用。

在α=6,l0=0.16和θ=20°和时，对于不同的温度参数γ=0.2,0.25,0.29,极化子基态能量E0随着外加电场强度F之间的变化关系曲线(图3)。结果表明，随着电场强度F的逐渐增大，极化子基态能量E0将逐渐减小。同时，还可以发现，当外加电场强度保持不变时，极化子基态能量E0随着温度参数的减小(温度增大)而逐渐增大(图3)。

图3 不同温度参数下，外加电场强度F与 图4 不同电子-声子耦合强度下，温度参数γ与极化子基态能量E0的变化关系曲线 极化子基态能量E0的变化关系曲线

在F=10,l0=0.16和θ=20°时，对于不同的电子-声子耦合强度α=6,7,8，极化子基态能量E0随着温度参数γ的变化关系曲线(图4)。结果发现，随着温度参数γ的升高，极化子基态能量E0几乎保持不变。换句话说，当温度参数变大时，温度对极化子基态能量E0的影响是非常弱的，而电子-声子之间的耦合强度α对极化子基态能量E0的影响非常显著。但是当温度参数迅速减小时，电子-声子之间的耦合强度对极化子基态能量的影响不显著，而温度对其影响较大。

对于不同的温度参数γ=0.02,0.09和不同的电场强度F=10,20时，极化子基态能量E0随着角参量θ的变化关系(图5(a)和(b))。结果表明，极化子基态能量E0周期性的随着角参量θ变化。当角参量取值在36°～45°,56°～67°和79°～86°之间时，极化子基态能量E0周期性的随着角参量的增大而增大。然而，当角参量取值在45°～55°和67°～79°之间时，极化子基态能量E0周期性随着角参量θ的增大而减小。这种现象来源于三角形受限势。

图5 不同温度参数(a)和不同电场强度下(b)，极角θ与极化子基态能量E0的变化关系曲线

3 结论与讨论

对于电子-LO-声子强耦合的情形，本次使用Pekar类型的变分方法研究了三角势量子点中极化子的基态能量。从而得到了极化子基态能量与量子点受限长度、外加电场强度、角参量和温度参数之间的变化关系。数值结果表明：在低温情况下，电场强度和量子点受限长度对极化子基态能量的影响起主要作用，而在高温和受限长度足够大时，温度对极化子基态能量的影响起主要作用。