一类非线性系统模糊自适应固定时间量化反馈控制

王焕清 陈 明 刘晓平

量化控制问题一直以来受到很多学者的广泛关注,作为网络控制中不可或缺的重要环节,旨在通过量化器把连续信号转换为在有限集中取值的分段信号.尤其随着数字设备性能的提高及网络化系统的应用和发展,量化控制已然成为解决网络化控制问题最有效的方法之一.

近年来,非线性系统的量化控制问题成为了一个新的研究热点[1].文献[2]针对一类非线性系统,提出了一种对数量化反馈控制器设计方法.文献[3]探讨了一类非线性离散系统的量化反馈控制问题,利用具有可数个固定控制输入的方法,解决了用“可数”去镇定“不可数”问题.在文献[4]中,基于Lyapunov 稳定性理论和线性矩阵不等式研究了包含均匀量化器的非线性系统的一致有界稳定问题.文献[5-6]针对具有量化输入的非线性系统,研究了自适应控制问题.

在工程实践中,系统的暂态性能是非常重要的.一般来说,为了提高生产效率,要求系统满足一定的快速性.如调节时间不能太短,容易造成系统机械冲击,影响设备使用寿命;反之,调节时间也不易过长,影响生产效率.固定时间控制是一种改善系统暂态性能的有效控制策,保证系统具有快速收敛性的同时,收敛时间存在确定上界,且与系统初始状态无关.文献[7]在最早的研究中首次提出了固定时间稳定的概念.基于此,文献[8-9]研究了非奇异固定时间控制问题,给出了固定时间收敛控制器的设计方法.文献[10]针对一类具有模型不确定性和外部扰动的时变非线性系统,研究了固定时间收敛特性的终端滑模控制问题.文献[11]研究了具有输出受限多输入多输出非线性系统的自适应固定时间控制问题.当前,随着对模糊控制/神经网络技术研究的不断深入,非线性系统自适应模糊控制和神经网络控制相关成果不断涌现,尤其利用反演控制算法,设计了很多不同的自适应控制算法解决非线性系统控制问题[12-15].

上述文献提出的方法有效地解决了某些特定非线性系统控制问题,然而针对非线性系统的模糊自适应控制尚有研究空间.例如,针对非线性系统的模糊自适应固定时间量化反馈控制,成果不多.因此,受上述文献启发,本文将固定时间控制、量化反馈控制及模糊控制等相结合,基于李雅普诺夫有限时间稳定理论和反演控制算法,研究具有迟滞量化器的非线性系统实际固定时间量化反馈控制问题.拟解决如下问题:1) 针对一类严格反馈不确定非线性系统,提出一种使系统实际固定时间稳定的控制策略,能够保证系统的跟踪误差在固定时间内收敛于原点的一个很小邻域内,且收敛时间与系统初始状态无关;2) 针对具有迟滞量化器的非线性系统,利用反演控制算法,基于李雅普诺夫有限时间稳定性理论,设计模糊自适应量化反馈控制器,使得闭环系统的所有信号均有界.最后,通过一个仿真示例验证了设计方法的有效性.

1 系统描述及预备知识

1.1 系统描述

考虑如下一类严格反馈非线性系统

其中,(t)=[x1(t),···,xi(t)]T∈Ri,i=1,···,n,y(t)∈R分别表示系统的状态变量及输出变量;gi(·),fi(·)为原点邻域内未知光滑非线性函数.

为了增加新的量化水平、避免量化信号的快速切换及抖振问题,本文选取如下迟滞量化器[16]

本文的控制目标为:确定区间Ω={0,±uj,±uj(1+δ)}和控制输入u(t),使得量化反馈控制器Q(u(t))确保系统的跟踪误差在固定时间内收敛于原点的一个很小邻域内,并且闭环系统的所有信号实际固定时间稳定.

根据文献[17],量化输入Q(u(t)) 可以描述为

且满足如下条件

1.2 预备知识

下面的定义、引理及假设对系统自适应实际固定时间量化反馈控制起了重要作用.

定义1[18].考虑系统

其中,x(t)∈Rn是系统的状态变量,f(·)为光滑非线性函数.若系统(6)是李雅普诺夫意义下稳定,若存在有限收敛时间Ts(x0),对于所有时间t ≥Ts,x(t)=0 恒成立,且收敛时间Ts存在与状态变量无关的确定上界,则该系统是固定时间稳定的.

引理1[18-20].考虑系统(6),若存在正定函数V(x)及正实数μ1,μ2,χ ＞1,0＜ϑ ＜1,满足

则称系统(6) 是固定时间稳定的,其收敛时间为

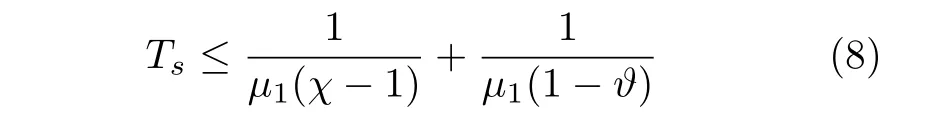
进一步,若存在正常数1,1 和0＜＜∞,使得

成立,则该系统是实际固定时间稳定.

注1.为了证明推导方便,在后面的设计过程中,令引理1 中的参数ϱ=1,χ=0.75,ϑ=2.

引理2[21].对于x∈R及∀ε＞0, 满足

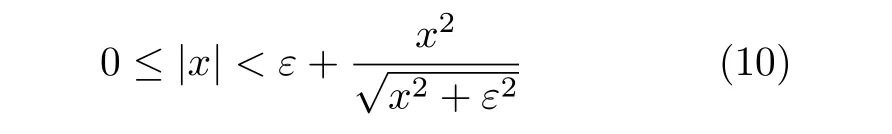
引理3[19].κi∈R,i=1,···,n及o∈(0,1],有

引理4[11].对于xi≥0,下列不等式成立

引理5[22].对于o1＞0,o2＞0,o3＞0,γ1≥0,γ2≥0,γ3≥0,如下不等式成立

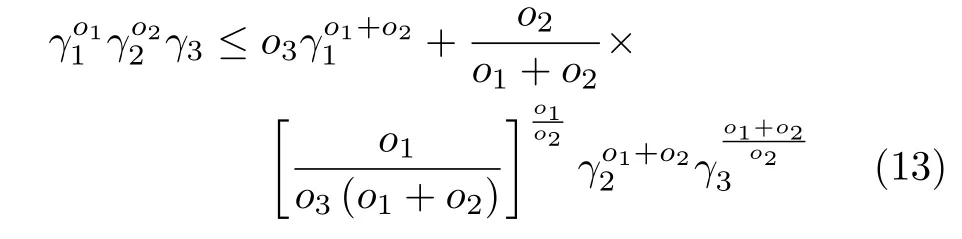
引理6[11].对于任意的ϵ＞0,下式成立

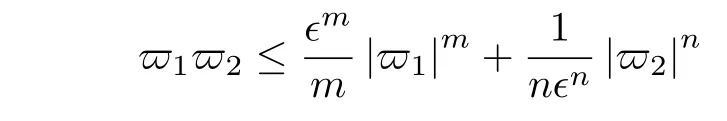
其中,m＞1,n ＞1 且(m-1)(n-1)=1.

引理7[22].函数f(Z):Rq→R是在紧集 ΩZ中定义的连续函数,对于任意常数τ＞0,存在模糊 逻辑系统WTR(Z)使得

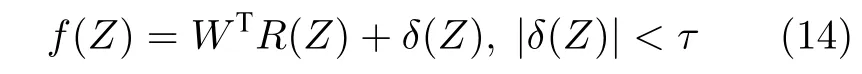
其中,δ(Z)为逼近误差,W=[w1,w2,···,wl]T∈Rl表示权值向量,R(Z)=[r1(Z),r2(Z),···,rl(Z)]T,ri(Z)=exp[-(Z-ςi)T(Z-ςi)/]是模糊基函数向量,这里,i=1,2,···,l,ςi=[ςi,1,ςi,2,···,ςi,l] 是基函数的中心,ηi是基函数的宽度.

假设1[11].系统(1)中的函数gi(·)(i=1,···,n)有界,即:存在正常数0,使得

不失一般性,假设gi(·)为严格正的.

假设2[11].输出跟踪信号yr(t)及其直到n阶导数 均为连续有界.

2 控制器设计

2.1 设计过程

本节中,应用反演算法,在假设1 和假设2 下设计实际固定时间跟踪控制器.首先,引入如下坐标变换

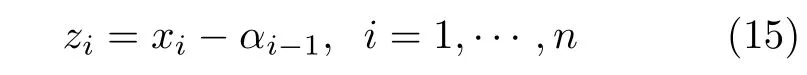
其中,αi-1是虚拟控制律,α0=yr.整个控制器设计过程分n步,具体为:

步骤1.根据式(1)和式(15),有

考虑如下Lyapunov 函数

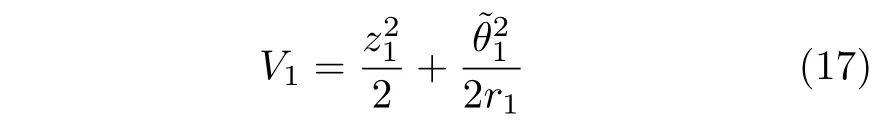
其中,=θ1-,是θ1的估计,r1为大于零的设计参数.

它的时间导数为

其中,δ1(Z1)为逼近误差,Z1=[x1,yd,].

利用完全平方公式,z1Λ1可以表示为

其中,θ1=‖W1‖2.将式(20)代入到式(18),得到

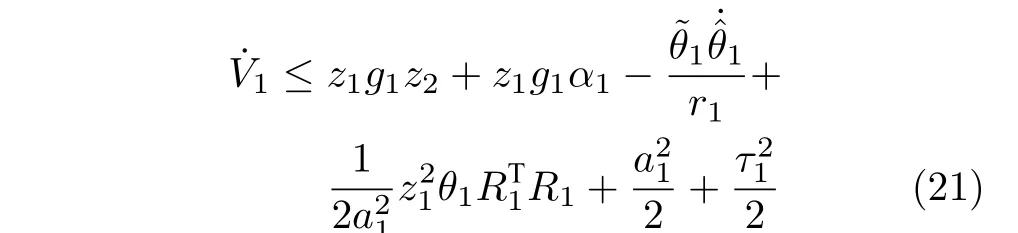
设计第1 个子系统的自适应律和虚拟控制律α1为

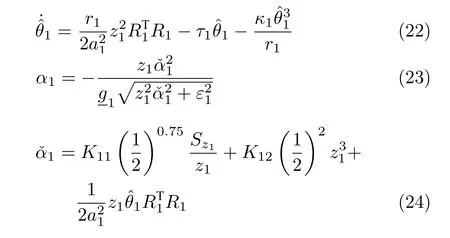
其中,a1,K11,K12,κ1,ε1均表示正的设计参数,且Sz1定义为

其中cj(j=1,···,n)各系数由如下方程计算求得:

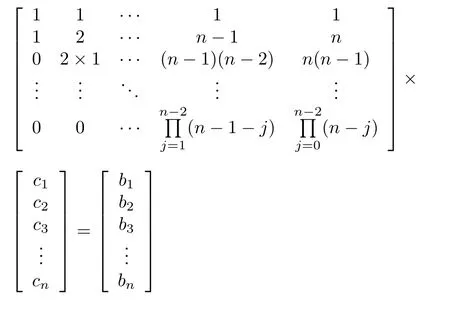
注2.上述分析过程仅考虑了当|z1|≥ε10的情形.当|z1|＜ε10时,通过重复上述的分析过程,可以得出式(27)中存在一个有界的附加项,其可以看作是式(27)中常数项σ1产生的一个微小增量.为了讨论方便,在理论分析过程中仅讨论|zi|≥εi0的情况.

步骤i(2≤i ≤n-1).考虑第i个子系统,对zi求导得

定义李雅普诺夫函数Vi为

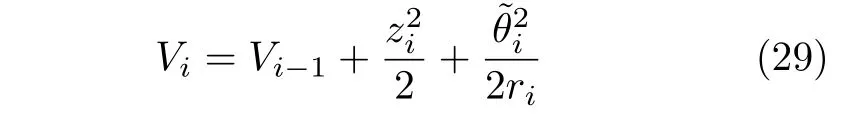
计算Vi的导数,得

根据完全平方公式,如下不等式成立

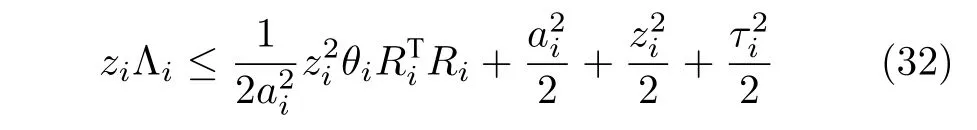
其中,θi=‖Wi‖2.

设计自适应律和虚拟控制αi为

其中,参数cj的取值与式(25)相同.

根据式(34)和式(35),得

结合式(30)～(37),如下不等式成立

步骤n.构造李雅普诺夫函数

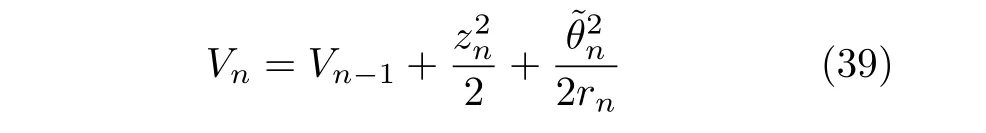
利用式(15),于是

结合式(3)和式(40),计算Vn的导数,得

利用完全公式,式(4)和式(5),如下不等式成立

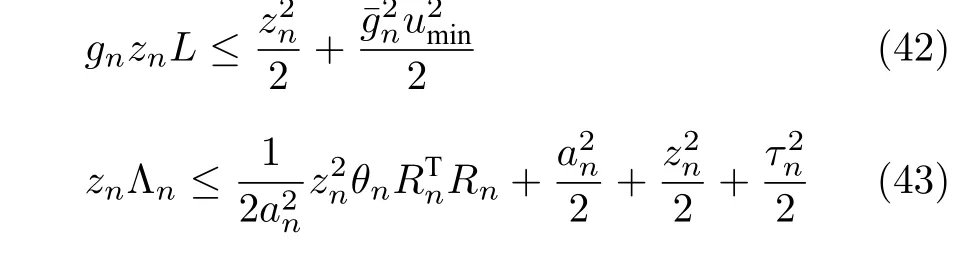
其中,θn=‖Wn‖2.

将式(42)和式(43)代入式(41),得到

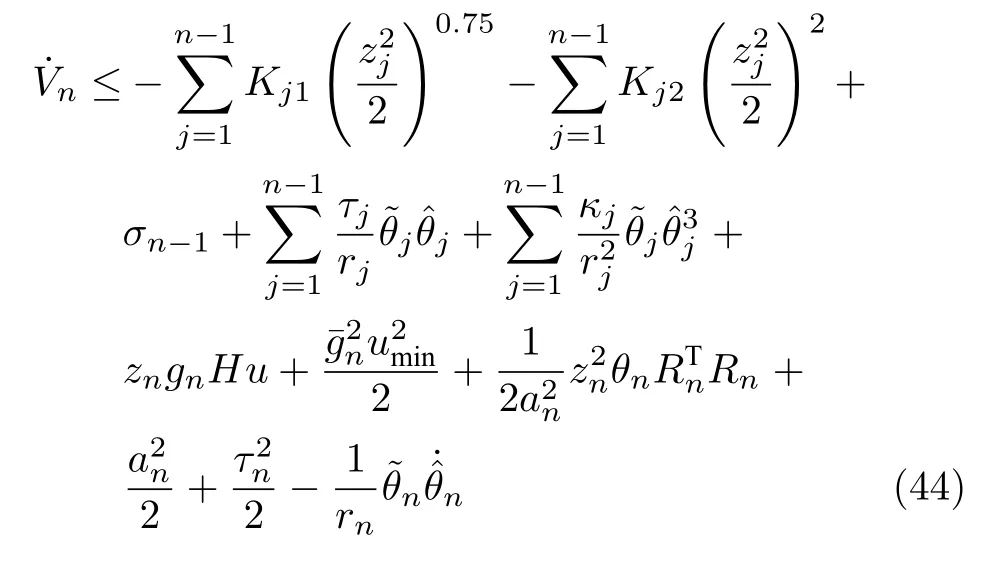
其中,an,Kn1,Kn2,κn,εn均为大于零的设计参数,且Szn定义为

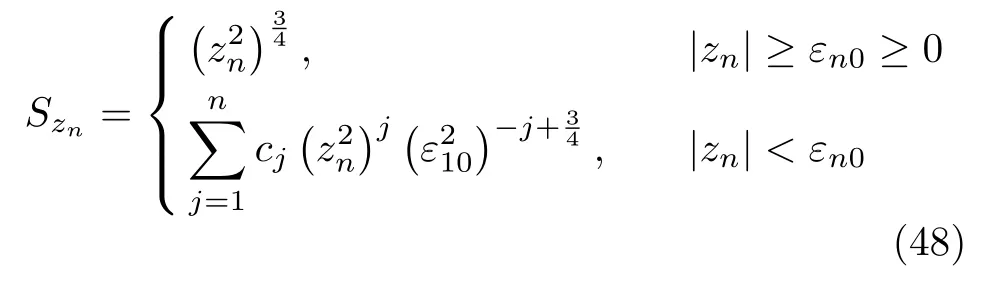
根据式(4),式(46)及引理2,得

将式(45),式(47)和式(49)代入式(44),有

进一步,利用Young 不等式[11],可得

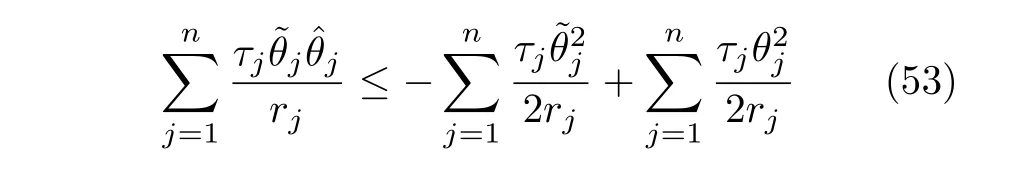
将式(51)～(53)代入式(50),有

显见,o3是大于零的正常数.

利用引理6,容易得到

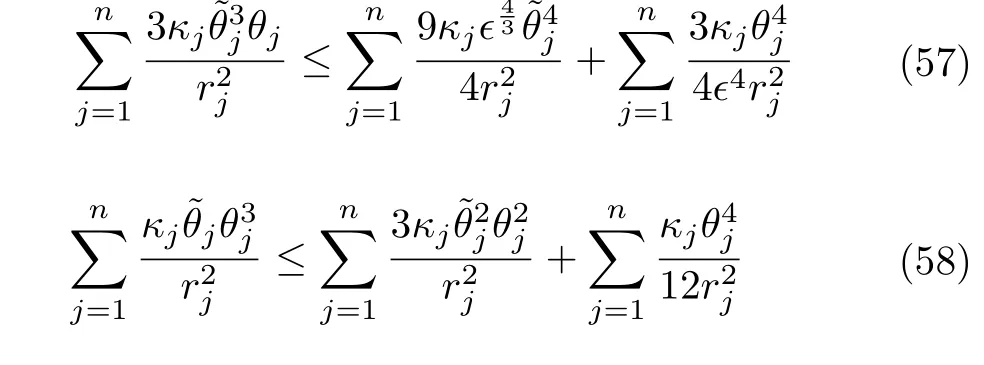
将式(57)和式(58)代入式(56),得到

至此,控制器设计过程结束.本文的主要结果可总结为第2.2 节中的定理1.

2.2 稳定性分析

接下来,基于引理1,对系统(1)进行稳定性分析.

定理1.考虑系统(1)在迟滞量化器(2)及满足假设1 和假设2 的条件下,设计实际控制律(46),并采用式(23)和式(34)所描述的虚拟控制律及式(22),式(33)和式(45)表示的自适应律,则

1) 被控系统(1)内所有信号均有界;

2) 系统的跟踪误差在固定时间内收敛于原点的一个很小邻域.

因此,称该系统是实际固定时间稳定的.

证明.根据引理1 和式(60),可知Vn有界,进而推出zi,有界.进一步,由式(23),(24),(34),(35),(46)和(47),可知αi及u有界.又因为zi=xi-αi,可确定xi的有界性.综上,闭环系统内所有信号均有界.

进一步,将式(60)变换成如下形式

3 仿真分析

下面将通过如下算例来验证本文所设计的控制算法的有效性.考虑如下非线性系统

根据定理1,设计系统(64)自适应固定时间量化反馈控制律.仿真过程中发现,设计参数的选择合适与否对系统性能有较大影响,通过反复试凑,选择如下设计参数:K11=K12=10,K21=K22=10,a1=a2=10,ε1=ε2=0.01,r1=r2=0.01,τ1=τ2=0.001,κ1=κ2=1;量化参数选择如下:δ=0.2,umin=0.1;系统初始条件为x1=0.2,x2=-0.5,=0.4,=0.1.

图1 表示系统实际输出和期望输出响应曲线,图2 绘制了跟踪误差响应曲线,从仿真结果可以看出,,跟踪误差收敛于原点的一个小邻域内.图3～6 分别为系统状态x2、控制输入u、量化输入Q(u)及自适应在固定时间内律的响应曲线,表明系统内所有信号均是有界的.仿真结果表明该系统是实际固定时间稳定的,验证了设计方案的有效性.

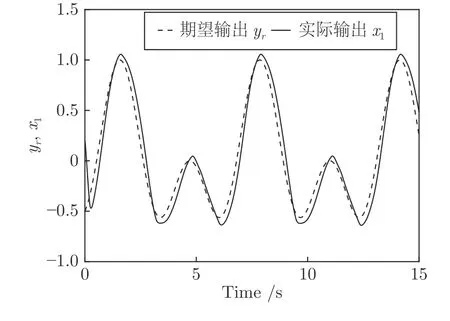
图1 期望输出和实际输出曲线Fig.1 Trajectories of desired output and practical output

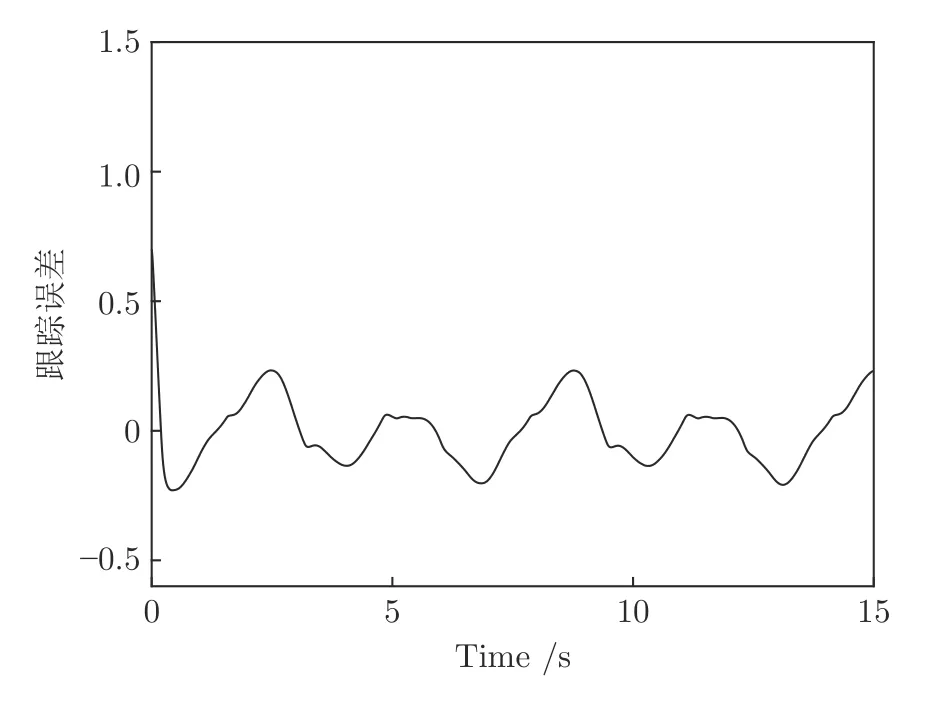
图2 跟踪误差响应曲线Fig.2 Response curve of tracking error

图3 状态变量x2响应曲线Fig.3 Response curve of x2

图4 控制输入 u 响应曲线Fig.4 Response curve of control input u

图5 量化输出响应曲线Fig.5 Response curve of Q(u)

图6 自适应律,响应曲线Fig.6 Response curves of adaptive control law ,

4 结论

本文针对具有量化输入的一类严格反馈非线性系统,基于有限时间Lyapunov 稳定理论和模糊控制方法等,研究了非线性系统的模糊自适应实际固定时间跟踪控制问题.所设计的控制器能够保证系统的跟踪误差在固定时间内收敛于原点的一个小邻域,同时保证闭环系统内所有信号有界.仿真算例验证了所提控制方案的有效性.值得指出的是,本文所得到的结果是在假设控制系统的所有状态变量可测的前提条件下成立,然而该假设条件在许多实际系统中难以满足.为此,下一步将考虑在状态不可测的条件下,研究基于状态观测器的固定时间输出反馈控制问题.