基于双向螺旋水套永磁同步电机散热特性研究
2022-01-13龚京风
龚京风,刘 帅
(武汉科技大学汽车与交通工程学院,湖北 武汉,430065)
近年来,国家将新能源汽车作为未来研发的重点方向,其中,以电动车用永磁同步电机(PMSM)为代表的驱动电机技术显著提高了电动汽车的性能和舒适性。由于PMSM功率密度高,其产生的热量较高,要确保PMSM有效运行,就必须保证电机能够及时散热[1-6]。
关于电机温升与散热的研究,目前主要采用等效热网络法和数值计算法,前者计算速度快,后者计算精度高,但对计算机资源要求较高。文献[7-9]对电机的电磁损耗进行分析,通过等效处理和简化研究对象,提高了其数值计算的速度,且数值计算误差较小。针对PMSM的散热问题,目前主要采用在机壳中嵌入水道的方法,利用流体有效带走电机内部的热量,水道中流体的流动状态和流道的结构会对电机温升产生较大的影响,目前国内外研究人员在水道方面展开了诸多分析和优化设计。杨学威等[10]针对高功率密度电机的散热问题,综合考虑水道的散热效果和水道的压力损失,给出了轴向Z字型水道的设计方法;王晓远等[11]分析了不同因素对螺旋水套散热特性的影响,为车用电机冷却散热的研究提供了一定的参考;文献[12-13]对永磁同步电机端部绕组温升过高的问题进行研究,发现采用热管可以有效抑制额定功率下的电机绕组温升;吴柏禧等[14]设计了一种折返型水道,为水冷电机的流道设计提供了参考;王钰琦[15]对轴向 Z字型水道进行研究,发现在电机水道中加入扰流片可以提高其冷却效果。
目前电机水套大都采用单向水道冷却散热的方式,存在水套散热不充分、散热不均匀、压力损失大等问题,为此,本文以一台额定功率为80 kW的永磁同步电机为研究对象,采用一种错位布置的双向螺旋水套冷却散热方式,通过建立PMSM的电磁损耗数学模型和流固耦合传热数学模型,计算在额定工况下双向螺旋水套PMSM各部件的电磁损耗,仿真分析其温度场分布,并与单向螺旋水套对PMSM各部件的散热效果进行对比,以期为永磁同步电机散热的研究提供参考。
1 数学模型的建立
1.1 电磁损耗数学模型
电机运行时产生的损耗是电机发热的主要原因,损耗计算的正确与否直接影响电机温度场计算的准确性,其中绕组铜耗、铁芯损耗和永磁体涡流损耗是永磁同步电机损耗的主要来源,本文应用有限元数值计算方法分别求解电机各部位的损耗。
1.1.1 绕组铜耗
当趋肤深度大于导线半径时,近似认为导线内部的电流是均匀分布的,因此可不考虑集肤效应引起的铜耗变化,绕组铜耗(PCu)的计算公式为:
PCu=mI2R
(1)
式中,m为绕组的相数;I为电流的有效值,A;R为电阻的平均值,Ω。
1.1.2 铁芯损耗
铁芯损耗(PFe)包含磁滞损耗(Ph)、涡流损耗(Pc)和异常损耗(Pe)三部分,采用经典的Berttotti损耗分离方法进行计算,其计算公式为:
(2)
式中,kh为磁滞损耗系数;kc为涡流损耗系数;ke为异常损耗系数;f为频率,Hz;BP为磁通密度幅值,T。
1.1.3 永磁体涡流损耗
内转子内置式永磁体的涡流损耗一般较小,但由于转子内部的散热条件恶劣,对永磁体的温升影响仍然较大,永磁体涡流损耗(Pmag)的计算公式为:
(3)
式中,V为涡流损耗空间积分区间,m3;σ为永磁体的电导率,S/m;E为电场强度,N/C;Jw为电流密度,A/m2。
1.2 流固耦合传热数学模型
将水道中冷却液的流场与整机的温度场作为一个整体来求解,在不同的区域采用通用的控制方程,使冷却液与水道壁面之间的对流传热面成为耦合面,无需再设置该传热面的传热系数,采用流固耦合传热的仿真方法不但避免了传热面传热系数难以确定的问题,而且使仿真结果更符合实际。
水道中冷却液不可压缩,其流动处于湍流状态,通用控制方程为:

(4)

电机传热过程遵循能量守恒方程,其导热微分方程及边界条件为:
(5)
式中,λ为导热系数,W/(m·K);T为物体温度,K;Q为热源,W/m3;cp为比热容,J/(kg·K);T0为边界上已知的温度分布,K;q为边界面已知的热流密度,W/m2;h为传热系数,W/(m2·K);Te为周围介质温度,K。
2 电磁损耗计算分析
本文以12级72槽永磁同步电机为研究对象,电机的转子采用内置“V”型永磁体结构,其基本参数如表1所示。根据表1中的基本参数,利用Maxwell建立电机的电磁损耗模型如图1所示。
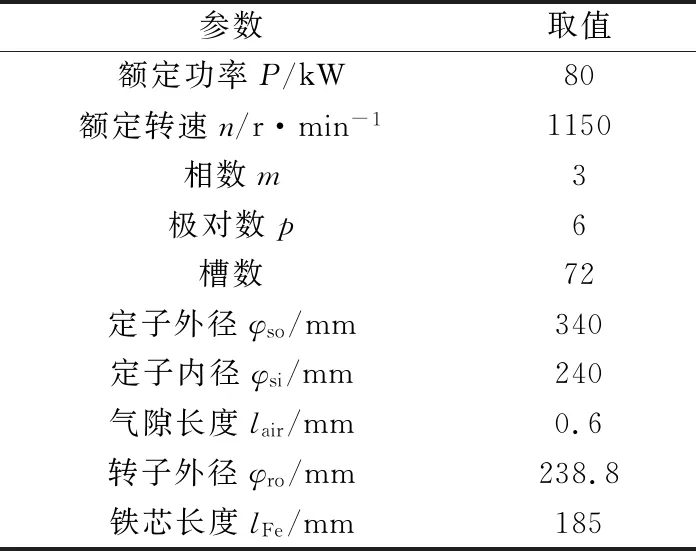
表1 PMSM基本参数Table 1 Basic parameters of PMSM
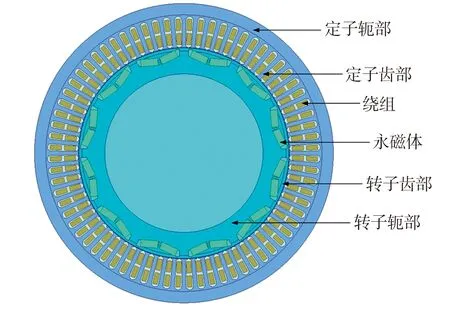
图1 PMSM电磁损耗模型Fig.1 Electromagnetic loss model of PMSM
PMSM铁芯损耗密度图如图2所示。从图2中可以看出,定转子铁芯中的磁密分布并不均匀,且铁芯齿部磁通密度往往要高于轭部的磁通密度,因此齿部比轭部的铁耗高出许多,为了更加精确地计算电机的温度场分布,以便对电机不同部位分别加载热源,将电机定转子齿部和轭部的铁芯损耗分开计算。此外,端部绕组和槽内绕组的散热条件相差较大,可按照实际用铜的体积比进行铜耗划分。基于建立的电磁损耗分析模型,在额定工况条件下,利用有限元法求得PMSM各部位的损耗,其中铁耗取周期性稳定后的平均值,PMSM铁芯损耗曲线如图3所示,PMSM各部位损耗的计算结果如表2所示。
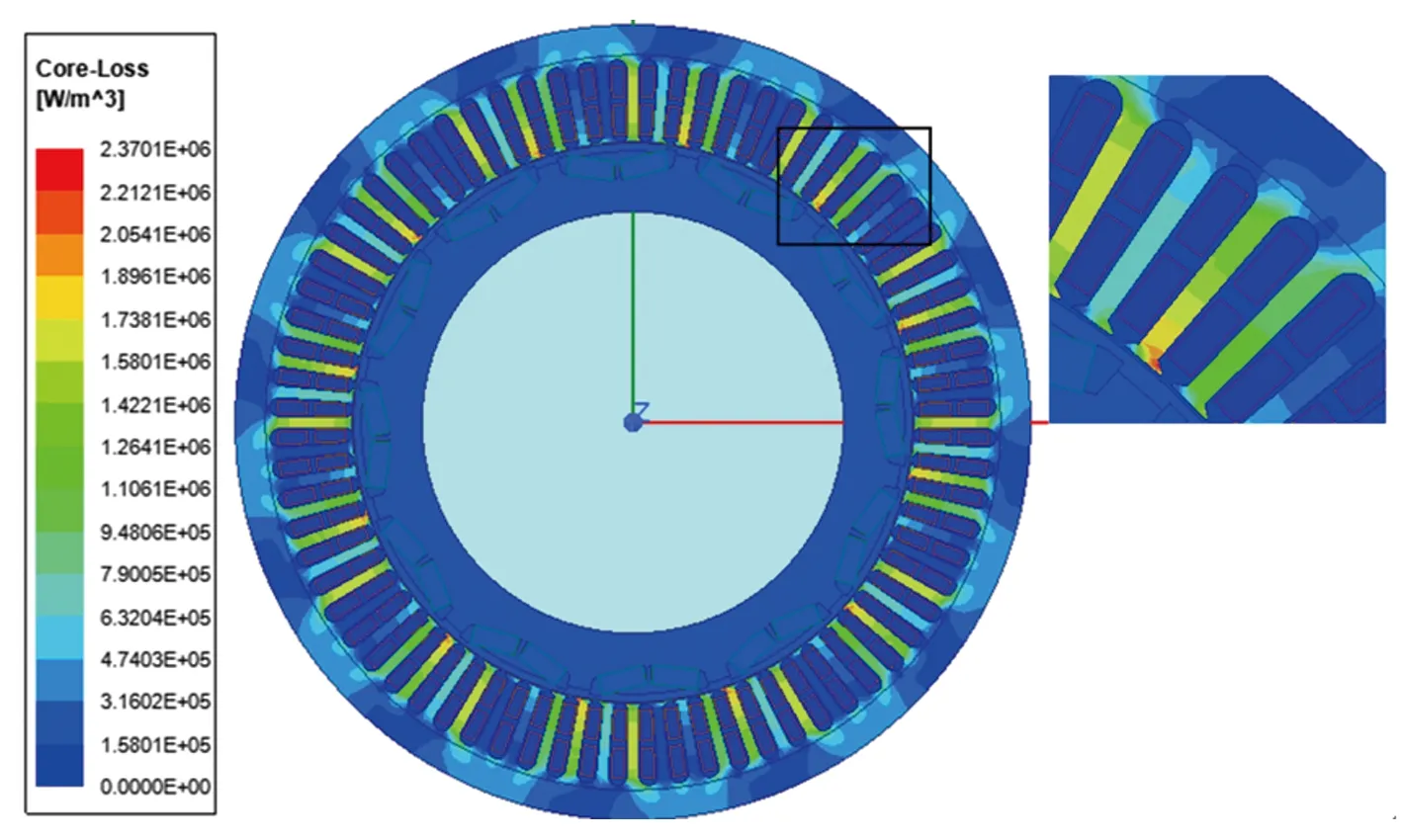
图2 PMSM铁芯损耗密度图Fig.2 Core loss density diagram of PMSM
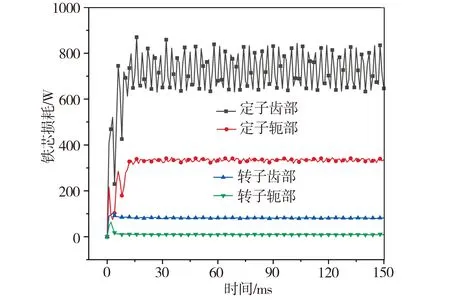
图3 PMSM铁芯损耗曲线Fig.3 Core loss curves of PMSM
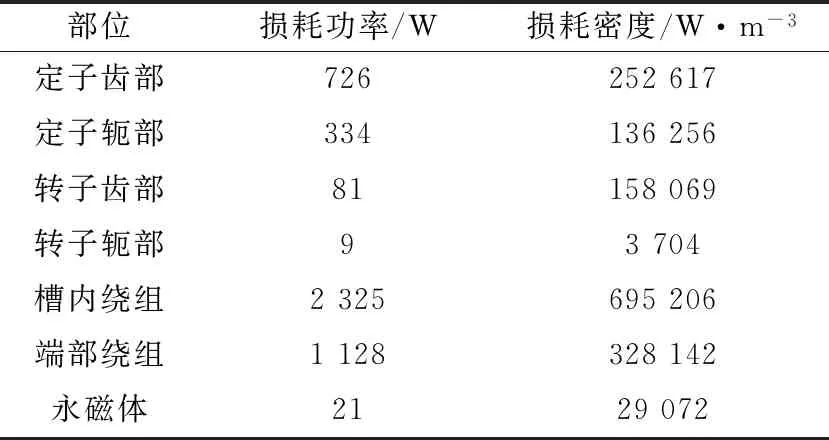
表2 额定工况下PMSM各部位的损耗Table 2 Loss of all parts of PMSM under rated operating condition
3 双向螺旋水套结构优化
3.1 双向螺旋水套的提出
现有电机水套种类繁多,虽结构差别较大,但大都采用单进单出的方式,随着冷却液的单向流动,带走电机内部热量的同时,冷却液的温度也会上升,因此不可避免地会存在驱动电机水套散热不足、散热不均匀等问题。若只是依靠增大冷却液流量的方式提高电机的散热效果,会导致水套的压力损失较大,水泵的负荷也会随之增加。鉴于现有单向水道存在的不足,本文提出了一种新型双向螺旋水套,采用错位布置的结构方式可以形成一对互逆的“S”型水道结构,如图4所示。双向螺旋水套可以采用普通单向螺旋水套的制造工艺,在整个散热系统中只需引入分流阀即可完成散热循环工作,因此具有较强的可操作性。

图4 双向螺旋水套结构示意图Fig.4 Schematic diagram of bidirectional spiral water jacket
3.2 计算模型的基本假设
因电机模型过于复杂,直接进行全三维模型计算将会占用较多的计算机资源和时间,研究水套本身的散热特性,可忽略电机内部的温升情况,现将传热模型做如下假设:
(1)电机内部所有热源等效为一个总热源,电机产生的热量基本通过水道冷却结构散发,绝少部分由机壳传递给周围的空气,不计辐射换热。
(2)电机外壳的表面为光滑平整的圆柱面,忽略其它外部结构的影响。
基于上述假设,将80 kW永磁同步电机的总损耗4.62 kW作为热源,已知水套内壁面的有效面积为0.1973 m2,则等效热流密度q为23.42 kW/m2,将其加载于水套内壁和定子接触面,作为热力学边界条件。
3.3 结构参数对双向螺旋水套散热特性的影响
水道截面结构示意图如图5所示。水道的结构参数主要包括其截面长(a)、宽(b)、径向高度(d2)以及水道间距(d1),为了保证水套具有足够的结构强度,d1、d2的取值不宜过小,在此将d1、d2、b设为定值,统一进水口体积流量为10 L/min,通过改变a的大小将水道的环数(N)调整为4~8环,并应用Fluent软件对双向螺旋水套进行流固耦合传热仿真分析。针对水道环数(N)为4、6、8三种结构进行温度场、壁面压力和流体流速的特征分析,仿真结果如图6所示。从图6(a)中可以看出,双向螺旋水套温度场呈中心对称式分布,从两侧至中间温度逐渐上升,温度场分布较均匀,不同于普通水套进、出口两侧温差较大的状况;当N=4时,双向螺旋水套的温度最高,其峰值温度为72.6 ℃,表明4环双向螺旋水套的散热效果最差;当N=6和N=8时,水套的峰值温度非常接近,仅相差0.3 ℃,表明两者的散热效果差距较小;从图6(b)中可以看出,三种水道的进水口压强均较大,且沿水路方向压强逐渐降低,当N=8时,双向螺旋水套的压力损失最大,这是由于随着环数的增加和水道截面的减小,会使螺旋水套中的流阻增大;从图6(c)中可以看出,三种水道的流速分布均匀,进、出口处由于有拐角的存在,其流速较快,且湍流明显,随着双向螺旋水套环数的增加,水道整体流速不断增大。
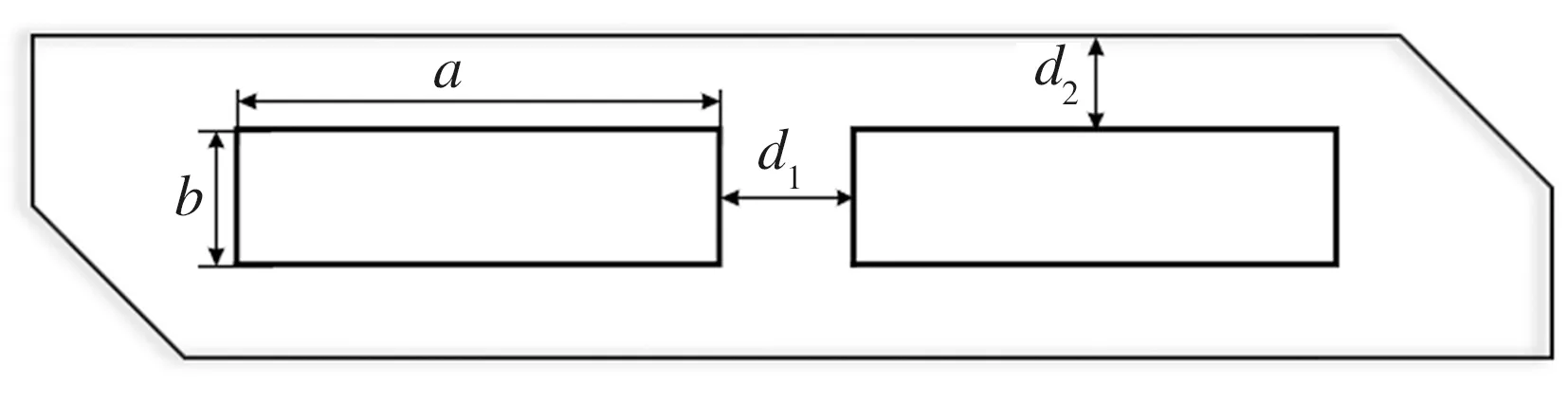
图5 水道截面示意图Fig.5 Schematic diagram of channel section
不同环数双向螺旋水套的散热特性如表3所示。结合图6和表3可以看出,虽然8环水套的散热效果最好,但其压差较大,在注入相同流量冷却液的情况下,则需外部水泵的功率也最大,制造
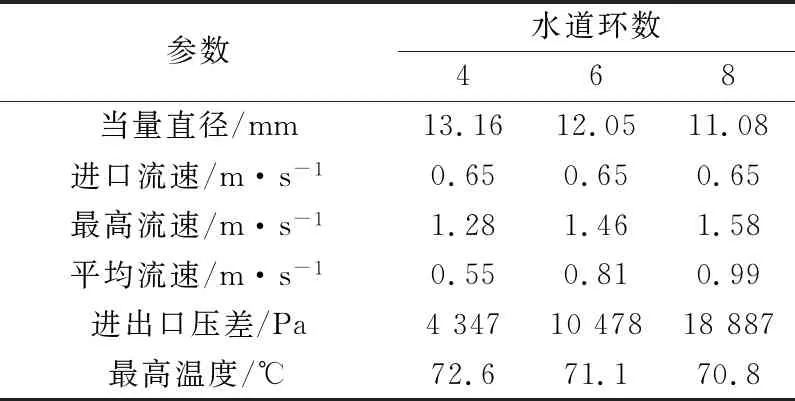
表3 不同环数双向螺旋水套的散热特性Table 3 Heat dissipation characteristics of bidirectional spiral water jacket with different numbers of loops
成本也会相应增加;4环水套的压差最小,但是其换热效果相对较差,温升较高。综合考虑水套中的流速、压差、冷却效果和水泵功耗及其制造成本等多方面因素,永磁同步电机采用6环的双向螺旋水套为最佳结构方案。
4 永磁同步电机温度场仿真分析
4.1 数值计算方法验证
因永磁同步电机模型过于复杂,为简化仿真计算和分析,作如下假设:绕组线圈用等效导体和等效绝缘层代替;各部件接触面采用等效热阻的方式处理;电机各部分损耗不随温度变化而变化;与空气接触的表面用经验公式计算的换热系数表示。
单向螺旋水套PMSM轴向截面温度分布云图如图7所示。为了验证额定工况下对螺旋水套进行流固耦合传热仿真计算的温度场结果是否准确,将相同条件下的仿真数据与实验数据[16]进行对比,单向螺旋水套的PMSM温度场计算值与实验值对比如表4所示。从表4中可以看出,本文计算结果整体较实验值偏低,存在一定偏差,但是PMSM各部件温度分布趋势基本一致;本文计算结果与文献计算结果吻合较好,这是因为数值仿真时考虑了各部件间接触热阻的影响,由此表明,本文基于流固耦合传热的计算方法可用于研究单/双向螺旋水套对PMSM温升特性的影响。

图7 单向螺旋水套的PMSM轴向截面温度分布云图Fig.7 Cloud diagram of temperature distribution of PMSM axial section of unidirectional spiral water jacket
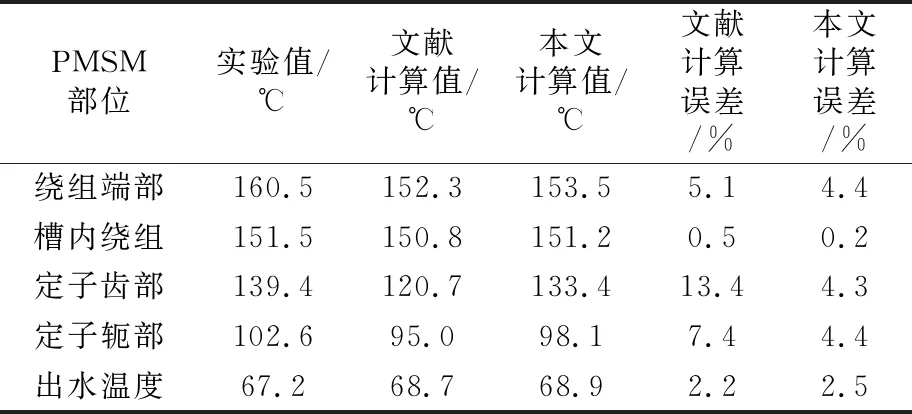
表4 单向螺旋水套的PMSM温度场计算值与实验值对比Table 4 Comparison between calculated and experimental values of PMSM temperature field of unidirectional spiral water jacket
4.2 螺旋水套的PMSM温度场计算与分析
为探究双向螺旋水套对PMSM各部件散热效果的影响,本文将与常用的单向螺旋水套进行对比分析。双向螺旋水套和单向螺旋水套的水道结构采用相同的截面和环数,其中N=6,水套中冷却液以及PMSM的初始温度均设定为65 ℃,冷却液的进口流量为10 L/min,当仿真达到稳态时,PMSM槽内绕组、定子铁芯、永磁体的的温度分布云图如图8所示。从图8中可以看出,相同条件下,双向螺旋水套的散热能力明显优于常用的单向螺旋水套,最高温度降低2~3 ℃。从图8(a)中可以看出,定子铁芯径向温差较大,这是因为定子铁芯轭部紧贴机壳,散热效果好,因此定子铁芯齿部温升较高,轭部温升较低;从图8(b)中可以看出,上、下层绕组存在温差,靠近定子铁芯齿部的绕组散热条件较靠近定子铁芯轭部的差,所以靠近定子铁芯齿部的绕组温度较高,由于端部绕组发热严重,散热条件又较差,所以端部温度较高;从图8(c)中可以看出,永磁体的整体温差并不大,由于存在气隙,永磁体的径向散热较少,而端部存在一定的对流换热,所以会出现两端温度低、中间温度高的状况。

(a)定子铁芯
由图8的温度分布云图还可以看出,两种水套的散热均匀性也存在一定的差异,为便于分析,截取PMSM轴/径向截面的温度分布云图以及沿轴/径向截线l1和l2(截取位置见图9)的温度变化曲线,分别如图9和图10所示。从图9(a)中可以看出,单向螺旋水套进水口和出水口的温度不一致,表明水套靠近进水口一侧比靠近出水口一侧的散热效果要好,这是由于水套中水的流动吸收带走PMSM中各部件产生的部分热量,使水温逐渐上升,导致其散热能力有所下降;从传热学的角度分析,由于定子铁芯紧贴水套内壁面,因此水套对定子铁芯的散热效果较好,而端部绕组的散热主要依靠与空气的对流换热,因此绕组沿轴向的温度梯度较大。从图9(b)中可以看出,双向螺旋水套的PMSM轴向整体温度较低,且分布较均匀,这是由双向螺旋水套轴向结构对称性所决定的。从图10(a)中可以看出,两种水套的PMSM沿轴向在进水口一侧的温度仅相差0.5~1 ℃,而在出水口一侧的温度却相差1~2 ℃,这表明双向螺旋水套可以弥补单向螺旋水套出水口一侧散热较差的问题;且从整体来看,双向螺旋水套散热效果好于单向螺旋水套。从图10(b)中可以看出,两种水套的PMSM沿径向的温度差逐渐变大,温差从贴近水套部位的1~2 ℃增加到内部的4~5 ℃,表明双向螺旋水套对PMSM内部各部件的散热能力更强。综上所述,双向螺旋水套可以克服单向水套出水口一侧散热较差的问题,且整体上对PMSM内部各部件的散热效果更好。
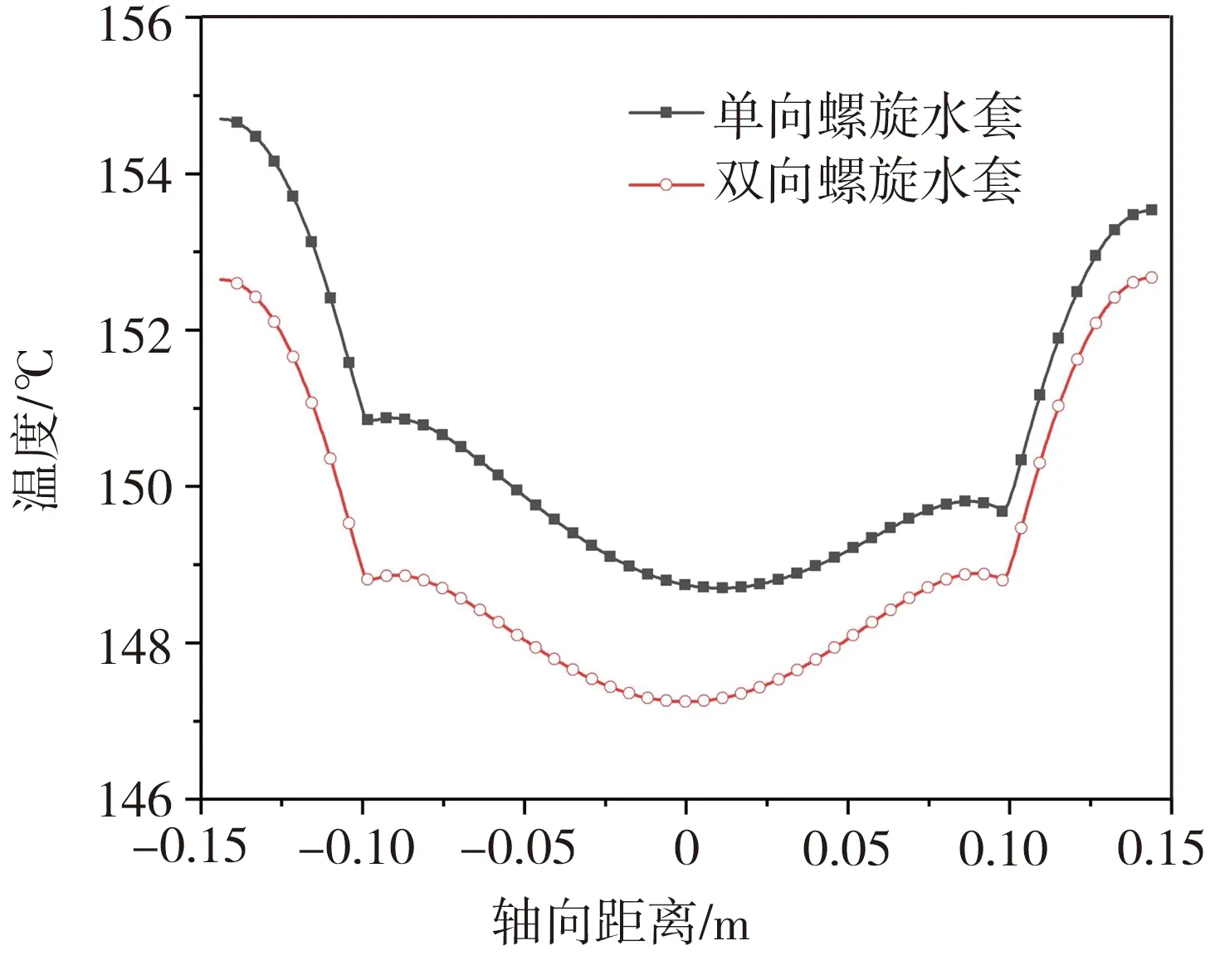
(a)截线l1
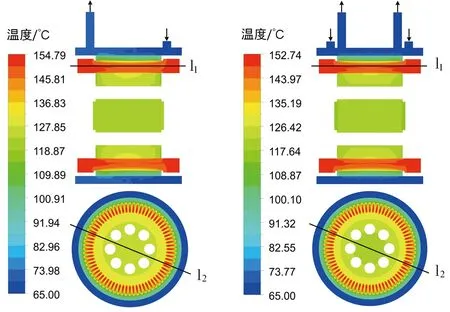
(a)单向螺旋水套N=6 (b)双向螺旋水套N=6图9 PMSM轴/径向截面温度分布云图Fig.9 Temperature distribution cloud of PMSM axis/radial section
4.3 冷却液流量对PMSM温度场的影响
注入不同流量冷却液的情况下电机各部件的平均温度和水套进、出口压力损失变化曲线如图11所示。从图11中的温度变化曲线可以看出,随着注入冷却液流量的增加,最开始PMSM温度下降比较明显;当流量在8~16 L/min范围时,电机温度下降趋势较为平缓;当流量超过16 L/min以后,电机温度下降十分缓慢,出现了热饱和现象;在注入相同流量冷却液的条件下,双向螺旋水套的散热效果总是优于单向螺旋水套,并且注入冷却液的流量越低,两者的散热效果差距越明显。此外,从图11中水套进、出口压力损失曲线可以看出,压差与注冷却液的流量基本呈线性分布,注入冷却液的流量越大,流体的压力损失就越大;图11中双向螺旋水套的压力损失为单程进、出口压差,明显小于单向螺旋水套的压力损失,而实际上双向螺旋水套双程进、出口的总压力损失要大于单向螺旋水套的压力损失,特别是当流量超过16 L/min时,双向螺旋水套总的压力损失约为单向螺旋水套的1.3倍,表明当流量超过16 L/min后,流量的增加不仅对电机的降温效果不明显,反而会增加水套的压力损失,相反,双向螺旋水套在注入冷却液的流量较低时仍具有较好的散热能力,同时可减小水泵功率的消耗。在实际工程操作中,由于注入冷却液的速度过快,不仅对电机机壳的机械强度要求较高,而且在注入冷却液过程中会消耗更高的水泵功率,不利于节能。当注入冷却液的流量达到一定值后,继续增加冷却液流量对于电机的冷却效果并不明显,综合考虑节能以及冷却效果等因素,将注入冷却液的流量范围为8~16 L/min作为此水套的最佳流量选择区域。
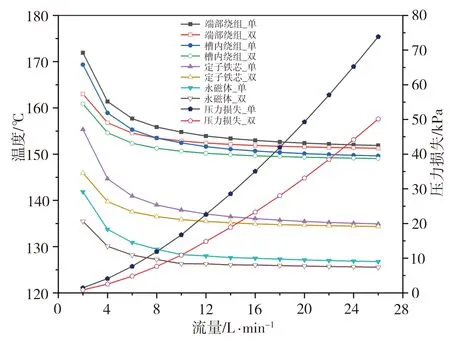
图11 PMSM温度和压力损失随注入冷却液流量的变化曲线Fig.11 Temperature and pressure loss change curves of PMSM with injection flow rate
5 结论
(1)与单向螺旋水套相比,双向螺旋水套对电动车用永磁同步电机内各部件的散热效果更好,且具有轴向散热均匀的优点。
(2)双向螺旋水套对永磁同步电机内定子铁芯和绕组的散热效果更加明显,克服了单向螺旋水套出水口散热不足的问题。
(3)在注入冷却液流量较低的工况下,双向螺旋水套对永磁同步电机也具有较好的散热效果。
