Riemann-Liouville分数阶时变时滞惯性神经网络的一致稳定性
2022-01-13李德宜邓宗娜冯育强
李德宜,邓宗娜,冯育强
(1.武汉科技大学理学院,湖北 武汉,430065;2.武汉科技大学冶金工业过程系统科学湖北省重点实验室,湖北 武汉,430065)
近年来,各类整数阶惯性神经网络得到研究者的广泛关注,如Cui等[1]利用线性矩阵不等式,得到了比例时滞惯性神经网络的全局渐近稳定性条件和全局鲁棒稳定性条件;Rakkiyappan等[2]利用矩阵测度法和Halany不等式,研究了具有时滞的惯性忆阻神经网络的周期性和同步性;Lakshmanan等[3]研究了具有离散分布时变时滞的惯性忆阻神经网络的全局指数耗散性;Zhang等[4]给出了离散分布时变时滞惯性神经网络全局Lagrange稳定性的几个充分条件,并给出了全局指数吸引集;Wang等[5]研究了具有反应扩散项和时变时滞的耦合惯性神经网络的采样数据同步问题。
分数阶微积分作为经典的整数阶微积分的推广,在描述一些系统时更为精准,有研究者将神经网络系统与分数阶微积分相结合,并对其稳定性进行研究,如Wu和Chen等[6-7]对分数阶忆阻神经网络的全局Mittag-Lefler稳定进行了研究;李倩等[8]研究了分数阶BAM神经网络平衡点的唯一存在性和全局渐近稳定性;Ke等[9-10]研究了分数阶时滞Cohen-Grossberg和BAM神经网络的有限时间稳定性;Gu等[11]研究了Riemann-Liouviue(R-L)分数阶时滞惯性神经网络模型的稳定性与同步性。
在神经网络应用过程中,由于两个神经元之间信号传输速度有限,不可避免地会产生时滞效应,特别是时变时滞,这在很大程度上会影响神经网络的同步性、稳定性和振荡性。为此,本文将文献[11]提出的R-L分数阶时滞惯性神经网络推广至R-L分数阶时变时滞惯性神经网络,基于R-L分数阶微积分有关性质,构造了Lyapunov-Krasovskii函数,并给出了判定R-L分数阶时变时滞神经网络模型一致稳定性的充分条件,最后通过实例分析,对该方法的合理性和有效性进行验证。
1 模型描述
R-L分数阶时滞惯性神经网络模型[11]可描述为:
0<β≤1,β≤α≤1+β,t>0,i=1,2,…,n
(1)
本文将上述模型推广至可用于描述时变时滞的情况,考虑模型如下:
t>0,i=1,2,…,n
(2)
式中:n表示神经网络中节点的数量;xi(t)表示第i个神经元的状态;ai、bi为常数,ai>0,bi>0;hj(t)为变时滞延迟量;fj和gj均表示神经元反应函数;fj(xj(t))表示神经元在t时刻的输出值;gj(xj(t-hj(t)))表示神经元在t-hj(t)时刻的输出值;cij表示在t时刻节点i与节点j之间的连接权重;dij表示在t-hj(t)时刻节点i与节点j之间的连接权重;Ii(t)表示外部输入量。
2 预备知识
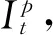
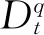
式中:Γ(·)为Gamma函数。
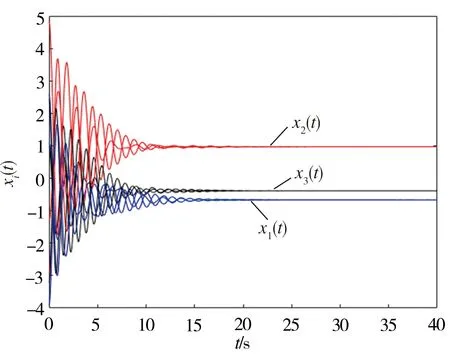
另外,当分数阶微分算子的阶数为-q(n-1≤q 此时,上式表示q阶分数阶积分。 性质3 a,b∈R,q>0 性质4 m,n∈Z+,n-1≤q≤n 性质5[13]R-L分数阶导数和分数阶积分有如下组合性质: 引理6[11]假设x(t)是[0,θ]上的连续可导函数,则 0 -hi(0)≤s≤0 本文中,始终假设神经元反应函数fi和gi满足Lipschitz条件,即存在正常数pi、qi,对于任意X1,X2∈R,满足 |fi(X1)-fi(X2)|≤pi|X1-X2| |gi(X1)-gi(X2)|≤qi|X1-X2| 引理8[11]若函数F(t)可导,且其一阶导数F′(t)连续,那么 (3) 证明:上述不等式(3)等价于 根据R-L导数的定义,有 同理, 于是, ((F(0)-F(t))2t-q- 证毕。 那么,式(2)对应的系统是全局一致稳定的。 -hi(0)≤s≤0 gj(xj(t-hj(t)))] (4) (5) 于是,式(4)可改写为 选取Lyapunov型函数如下: (7) gj(xj(t-hj(t))))vi(t)≤ 根据均值不等式,有 (8) 由式(8)可得 于是,在定理9的条件下,有 表明式(2)对应的时变时滞系统是全局一致稳定的,证毕。 采用Adams-Bashforth-Moulton预测校正法[14]对式(2)进行近似求解,并通过数值模拟方法对定理9进行验证。 考虑如下的分数阶微分方程: yh(tn+1)= 在实际仿真过程中,通过预测公式和校正公式的反复迭代,不断逼近理论真实值yh(tn+1)。 预测公式为: (n-j)q))f(tj,yh(tj)), 0≤j≤n 校正公式为: 其中 误差估计为 p=min(2,1+q) 例 考虑R-L分数阶变时滞惯性神经网络 t>0,i=1,2,3 本文采用的离散化算法中步长h=0.01。通过计算机数值模拟,可以得到该系统在3个不同初始值下,依次为(1.1,-1.3,1)、(2.1,-2.3,2)、(-2.1,2.3,-2),xi(t)(i=1,2,3)随时间变化的轨迹图如图1所示,可以看出,数值模拟结果与该定理相符,从而验证了本文所提出理论的准确性。 图1 不同初始值下xi(t)的轨迹图Fig.1 Trajectory diagram of xi(t)with different initial values 本文将R-L分数阶时滞惯性神经网络推广到R-L分数阶时变时滞惯性神经网络,并对其稳定性和同步问题进行研究。首先,基于Lyapunov直接法,构造了一个包含R-L分数积分项的Lyapunov-Krasovskii函数,并利用R-L分数阶导数和积分的组合性质,计算了Lyapunov函数的一阶导数,从而推导出R-L分数阶时变时滞神经网络模型一致稳定的条件。最后,通过数值实例验证了本文所提出理论的合理性和有效性。 另外,本文主要研究了分数阶为 的R-L分数阶时变时滞惯性神经网络,特别是当β=1时,分数阶惯性神经网络被简化为整数阶惯性神经网络。因此,整数阶惯性神经网络可以看作是分数阶惯性神经网络的一种特例。由此看来,本文提出的模型保守性较低,通用性较强。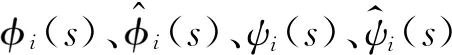
3 模型证明
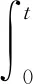


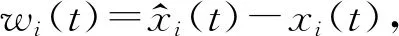
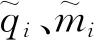
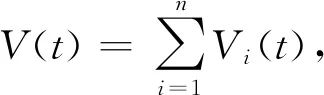
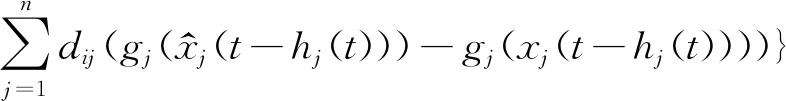
4 数值仿真
4.1 Adams-Bashforth-Moulton方法的基本原理
3.2 实例验证
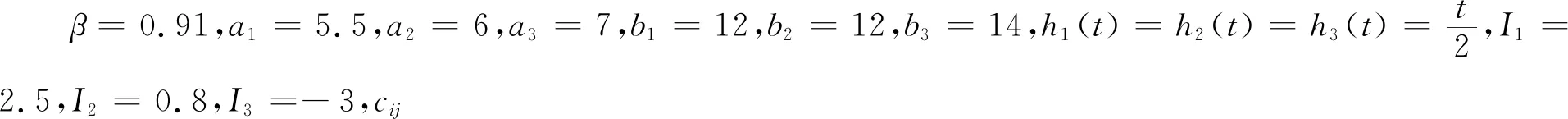
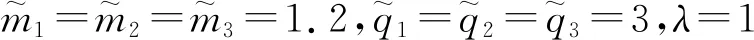
5 结语
