基于差分进化算法的FMS中机器与AGV同时调度方法

2022-01-12宋豫川吕向飞

重庆大学学报 2021年12期

伍乐，宋豫川，吕向飞，雷琦

(重庆大学机械传动国家重点实验室，重庆 400044)

在现代制造业生产中，多品种小批量、多样化个性化定制的生产模式已成为发展趋势，这必将会对柔性制造系统(flexible manufacturing system, FMS)提出更高的要求。生产调度是柔性制造系统的基础，制定科学合理的调度方案，对柔性制造系统的性能具有重要影响。其中，柔性作业车间调度问题(flexible job shop scheduling problem，FJSP)是非常复杂的NP难题。在以往的FJSP研究中，为了简化数学模型解决问题，大多忽略了工件在不同机器之间的运输时间，或将其包含在工件加工时间内，这都是不合理的，特别是当工件的移动完全依赖于自动导引小车(automated guided vehicle，AGV)并且运输时间与加工时间相当时[1]。因此，有必要对FMS中的机器与AGV同时调度问题进行研究。

针对机器与AGV同时调度问题，国内外学者进行了很多研究。早期，Bilge等[2]将问题表述为一个非线性混合整数规划模型，采用带滑动时间窗的迭代启发式方法进行求解。这种精确求解算法能够在简单小规模问题上取得全局最优解，但随着问题复杂度的增加，无法在合理时间内搜索到满意解。近年来，智能优化算法如遗传算法[3-8]、差分进化算法[9]、粒子群算法[10-11]、蚁群算法[12]、花授粉算法[13]等，在求解具有复杂约束的同时调度问题上，取得了较好的进步。Abdelmaguid等[3]提出一种新的启发式编码方案，采用混合遗传算法同时调度机器与AGV。Kumar等[9]提出机器选择和车辆分配两种启发式算法，并与差分进化算法相结合，为工件分配合适的机器与AGV，但没有对算法进行改进，仅对工序操作进行了基本差分变换。Zhang等[10]结合主粒子和嵌套粒子的特点，设计了一种改进粒子群优化算法来求解同时调度问题。

差分进化(differential evolution，DE)算法是一种基于种群进化的智能优化算法，具有全局搜索能力强，操作简单，鲁棒性好的优点。为了增强算法性能，通常需要对算法进行改进。Pan等[14]提出一种求解车间调度问题的离散DE算法，并结合局部搜索算法以改善算法性能。杨锋英等[15]提出一种改进DE算法求解AGV调度问题，设计了基于个体生存时间的种群更新机制以增强种群多样性，提高算法的搜索能力。吴秀丽等[16]针对分布式柔性作业车间调度问题，为离散DE算法设计了新的变异和交叉方式，并引入模拟退火方法以提高算法的局部搜索能力。

从现有文献来看，DE算法在求解复杂组合优化问题上能有较好的表现，但在机器与AGV同时调度问题上应用还较少。并且，大多文献把集成调度问题分解为了机器调度和AGV调度两个子问题，忽视了机器调度与AGV调度的紧密联系，以及忽略了可变工艺路线对AGV搬运的影响。因此，针对FMS中机器与AGV同时调度问题，在完善集成调度数学模型和改进算法性能方面有进一步研究价值。另外，当AGV数量大于1时，可能会发生冲突，对机器与AGV调度造成影响。但文中主要围绕零件加工尺寸较小的车间，其运输的AGV载重和尺寸也较小，虽然可能发生冲突，但是在车间区域内能并行通过，冲突问题产生的概率较小。

笔者针对FMS中机器与AGV同时调度问题，建立了以最大完工时间最小为优化目标的调度数学模型，提出了基于工序、机器、AGV的3层编码结构，以解决机器分配和AGV分配。针对DE算法易陷入局部最优的问题，设计了一种混合变邻域搜索的改进离散差分进化算法，以每次迭代的最优解作为局部搜索的初始解，设计了3种不同的邻域结构进行变邻域搜索，并采用种群更新策略以增强种群多样性，进而提升算法搜索到更好解的可能性。最后，通过对比实验，验证了所提算法求解FMS中机器与AGV同时调度问题的有效性和优越性。

1 问题描述及建模

1.1 问题描述

假设柔性作业车间有n个待加工工件在m台机器上加工，若干辆相同的AGV负责工件在机器之间运送。每个工件有ni道不同的工序，每道工序可选择的加工机器不唯一，每台AGV可以在任意两台机器之间运送工件。已知每个工件加工所需的工序，每道工序在对应加工机器上的加工时间，以及小车在不同机器间的运输时间，要求在满足一定约束条件下，为每道工序选择最合适的加工机器和搬运小车，确定每个工件的每道工序在各机器上的最佳加工顺序和开工、完工时间，以及在各AGV上的最佳搬运顺序和开始搬运、完成搬运时间，最终满足优化目标。

为了简化FMS中机器和AGV同时调度问题，假设条件如下：

1)零时刻，所有机器与AGV都可用，机器与AGV连续工作。

2)任意时刻，每台机器一次只能加工一个工件，每辆小车一次只能搬运一个工件。

3)同工件的工序有先后约束，不同工件之间无约束。

4)AGV数量提前确定。

5)AGV行驶速度恒定，其负重不影响小车行驶速度。

6)AGV在任意两台机器之间的运输路线是固定的，运输时间仅与机器之间的距离有关。

7)每台机器前设置有缓冲区，缓冲区无限大，以避免死锁。

8)所有待加工工件在开始加工前都放在装载台M0，完成所有工序加工的工件放入卸载台Mm+1。

9)小车每次执行完任务后停靠在加工机器旁，不返回起点。

10)小车没有装载工件的行驶过程称为空载，装载工件的运送过程称为负载。

11)不考虑AGV可能发生冲突、故障、电量不足等问题。

1.2 数学模型

为了建立问题的模型，引入如下符号和变量：

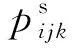
为了便于理解，变量的表示含义如图1所示。假设工序Oij在机器Mk上加工，工件i的前一道工序Oi(j-1)在机器Mk′上加工，工序Opq在机器Mh上加工。若小车Rv有一搬运任务Tij，需从当前位置Mh空载行驶至Mk′领取工件i，再从Mk′搬运工件i至Mk进行加工。

图1 变量含义示意图Fig. 1 Schematic diagram of variable meaning

以最大完工时间最小为优化目标，针对FMS中机器与AGV同时调度问题，建立数学模型如下。

目标函数：

(1)

约束条件：

1)每道工序一次只能分配给一台机器加工。

(2)

2)每道搬运任务一次只能分配给一辆小车运送。

(3)

3)同一辆小车，只有前一道任务Tpq搬运完后，才能开始下一道任务Tij的搬运。

(4)

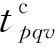
4)小车从当前的机器位置Mh行驶至该工件前一道工序的加工机器Mk′处领取工件。

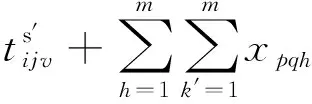
(5)

5)小车空载到达机器Mk′并且工序Oi(j-1)加工完成，才能开始搬运。

(6)

6)小车从机器Mk′搬运工件到工序Oij的加工机器Mk处进行加工。

对于宝宝来数，由于宫缩力度过强、频率过快、子宫收张的间隔太短，会导致胎盘血液循环受阻，宝宝易在分娩过程中出现缺血、缺氧。而且，胎儿出生过快，由于宫内和外界压力的变化，很容易造成宝宝皮肤下的毛细血管破裂，出现面部发红紫，严重者会引起头部血管破裂，发生颅内出血。胎儿骨折、产伤风险亦升高。

(7)

7)小车负载到达机器Mk并且机器空闲，才能开始加工。

(8)

8)工序Oij在机器Mk上加工。

(9)

2 混合变邻域搜索的改进离散差分进化算法

基本DE算法是基于实数编码的，主要作用于连续域的优化问题。而柔性作业车间的调度问题是离散的组合优化问题，所以需要改进DE算法的变异、交叉操作，以适应算法的离散搜索过程。同时，变邻域搜索(variable neighborhood search，VNS)算法能够有效避免算法陷入局部最优，提高算法的局部搜索能力。因此，提出混合变邻域搜索的改进离散差分进化(improved discrete differential evolutionVNS，IDDE-VNS)算法求解FMS中机器与AGV同时调度问题。

2.1 总体流程设计

IDDE-VNS算法的总体流程设计如图2所示。

图2 IDDE-VNS算法流程图Fig. 2 Flow chart of IDDE-VNS algorithm

具体步骤如下。

步骤1：输入调度信息，工件加工信息和小车运输时间。设置DE算法控制参数，初始种群规模P，最大迭代次数Gmax，变异概率F，交叉概率Cr，小车数量Nagv，初始温度T0。

步骤2：根据编码方式和初始种群规模，随机生成初始种群。

步骤4：全局搜索。

1)根据变异概率F，选择初始目标种群X执行变异操作得到变异种群V。

2)根据交叉概率Cr，对目标种群X与变异种群V进行交叉操作得到试验种群U。

3)重新计算试验种群U的适应度值。

4)引入模拟退火思想，比较目标种群X与试验种群U，按退火概率选择相应的个体进入下一代。

2.2 详细设计

2.2.1 编码和解码方法

为了表示问题的解，首先需要设计编码。算法的性能和效率很大程度上取决于染色体的编码，需要考虑染色体的可行性、完备性、健全性和非冗余性。对于FMS中机器与AGV同时调度问题，不光要安排工序的加工顺序，还要确定每道工序的加工机器和每次负责搬运的小车。因此，编码分为3个部分。第1行表示基于工序的编码，第2行表示基于机器的编码，第3行表示基于AGV的编码。为了便于解释编码过程，采用一个3×3FJSP算例来描述，其工件加工信息如表1所示。2台AGV在任意机器之间的运输时间如表2所示。

表1 FJSP算例的工件加工信息

表2 各机器之间AGV的运输时间

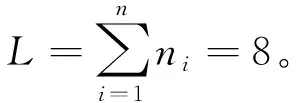
图3 基于工序、机器、AGV的3层编码结构Fig. 3 The three-layer coding structure of operation, machine and AGV

考虑AGV约束的柔性作业车间调度问题解码时，比传统的车间调度问题更加复杂。除了要确定每个工件的每道工序的开工时间和完工时间，还要确定AGV运送工件的空载、负载开始和完成时间。针对1个工件的某道工序Oij加工过程，如图1所示，设计解码方法如下。

1)确定AGV运送工序Oij空载、负载开始和完成时间，具体步骤如下。

步骤1：读取由上述编码方式生成的染色体信息，工序顺序P、对应加工机器Mk和运送小车编号Rv。

步骤2：记录AGV当前位置及其走过的路径。

步骤3：判断本道工序Oij是否为工件i的第1道工序。若是，跳转步骤4；若否，跳转步骤6。

步骤4：判断AGV的当前位置是否在装载台M0。

①若是，AGV空载运输时间t′= 0。

②若不是，AGV需要从当前位置Mh行驶到装载台M0领取工件，AGV空载运输时间t′=Mh→M0。

步骤5：AGV从装载台M0运送工件行驶到本道工序的加工机器Mk处，AGV负载运输时间t=M0→Mk。

步骤6：判断AGV的当前位置是否在紧前工序加工机器Mk′处。

①若是，AGV空载运输时间t′= 0。

②若不是，AGV需要从当前位置Mh行驶至该工件的前一道工序的加工机器Mk′领取工件。若该工件正在机器Mk′上加工，需等待加工完成后再搬运。AGV空载运输时间t′=Mh→Mk′。

步骤7：AGV从紧前工序加工机器Mk′运送工件行驶到本道工序的加工机器Mk处，AGV负载运输时间t=Mk′→Mk。

步骤8：输出AGV空载开始和完成时间，负载开始和完成时间。

2)确定工序Oij的开工时间和完工时间。

(10)

(11)

根据设计的编码和解码方法，结合工件的加工信息和2台AGV的运输信息，随机产生一个可行调度方案，其甘特图如图4所示。分析甘特图可知，工件加工过程和小车的运输过程具体如下，其中“*→”表示AGV空载运行。

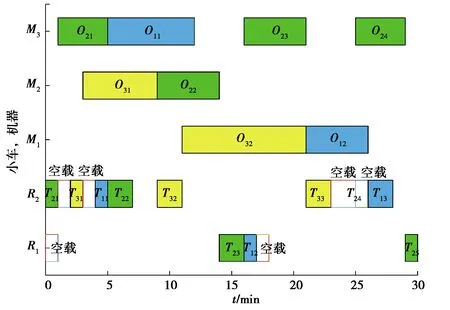
图4 调度方案的甘特图Fig. 4 Gantt chart of scheduling scheme

R1的运输过程：M0*→M2(取工件2)→M3(加工O23并取工件1)→M1(等待加工O12)*→M3(取工件2)→M4(工件2完成加工后运到卸载台)。

R2的运输过程：M0(取工件2)→M3(加工O21)*→M0(取工件3)→M2(加工O31)*→M0(取工件1)→M3(加工O11并取工件2)→M2(等待加工O22并取工件3)→M1(加工O32)→M4(工件3完成加工后运到卸载台)*→M3(加工O24)*→M1(取工件1)→M4(工件1完成加工后运到卸载台)。

2.2.2 全局搜索

根据上述编码方式，为了使个体直接在离散域搜索，以提高算法搜索速度，对DE算法的操作算子进行了改进。

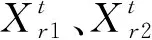
(12)

(13)

(14)

对基于工序编码的基因串，采用IPOX交叉[18]。其具体交叉过程为：将工件集{1,2,…,n}随机分为非空互补的两个子集S1和S2，复制父代染色体P1中包含S1的工件号到子代染色体C1，复制P1中包含S2的工件号到C2，保留它们的位置；同样复制P2中包含S1的工件号到C1，复制P1中包含S1的工件号到C2，也保留它们的位置，如图5所示。

图5 IPOX交叉过程图Fig. 5 Crossover process of IPOX

对基于机器编码的基因串，采用MPX交叉[18]。其具体交叉过程为：首先随机产生一行长度与父代染色体相等，由0和1组成的基因串。将父代染色体P1中1对应位置的机器号复制到子代染色体C2，父代染色体P2中1对应位置的机器号复制到C1，P1中剩余的机器号保留到子代C1，P2中剩余的机器号保留到子代C2，如图6所示。

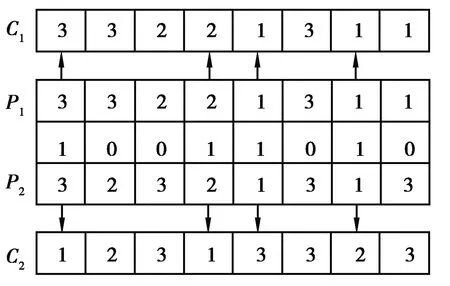
图6 MPX交叉过程Fig. 6 Crossover process of MPX

对基于AGV编码的基因串，采用简单的两点交叉。

(15)

(16)

式中，T为退火温度，为了提高算法搜索效率，采用自适应变温方法，不进行循环。T的变化见式(17)。

(17)

2.2.3 局部搜索

变邻域搜索算法比单一的邻域搜索算法性能更强，它通过改变算法的邻域结构来扩大其搜索范围，从而找到更优解。文中对当前种群中的最优个体执行变邻域搜索，以提高DE算法的局部搜索能力。

设计VNS算法首先需要构造邻域结构，算法采用了以下3种邻域结构来产生局部最优解：

1)邻域结构N1。在基于工序编码的染色体上，随机选择2个基因位置，所选的2个位置对应2道不同工件的工序，互换这2个位置。

2)邻域结构N2。在基于机器编码的染色体上，随机选择1个基因位置，所选位置对应工序的可加工机器不唯一，重新从该工序的可选机器集合中选择不同的机器替换该位置的机器。

3)邻域结构N3。在基于AGV编码的染色体上，随机选择1个基因位置，从可选AGV集合中选择不同的AGV编号替换该位置的AGV编号。

基于上述3种邻域结构，变邻域搜索算法的操作步骤如下。

步骤1：算法初始化，将全局搜索得到的最优解设为初始解X，设置q←1，qmax=3，cmax=40。

步骤2：判断循环终止条件q>qmax是否满足，若满足，输出最优个体；否则，转到步骤3。

步骤3：振动环节。初始解X通过邻域结构Nq搜索得到1个扰动解。

步骤4：局部搜索。

①以振动后的新解作为局部搜索的初始解X′，设置c←1。

②判断循环终止条件c>cmax是否满足，若满足，输出局部最优解X′；否则转到步骤③。

③使当前解X′在Nq中搜索得到一个新解X″，若满足f(X″)

④设置c←c+1，返回步骤②循环。

步骤5：判断邻域移动条件f(X′)

3 实验分析

实验测试以MATLAB2016b为开发环境，运行环境为Intel Core i5-6200 CPU，2.40 GHz主频，4 GB内存。

为了验证IDDE-VNS算法的性能，展开以下测试实验：

1)算法对比试验。针对遗传算法、差分进化算法和混合变邻域搜索的改进差分进化算法，对比这3种算法产生的解的质量，为客观评价提出的改进方法提供依据。

2)非柔性算例实验。选取Bilge等[2]提出的82个算例中的一部分进行实验，与其他文献使用各种优化算法得到的计算结果进行对比，为客观评价IDDE-VNS算法的性能提供依据。

3)柔性算例实验。选取Zhang等[10]提出的柔性算例进行计算，并与Zhang等[10]得到的优化结果对比，为客观评价IDDE-VNS算法作用在柔性作业车间时的性能提供依据。

3.1 算法对比实验

为了验证提出的改进方法的有效性和可行性，采用Bilge等[2]提出的测试算例中的EX11算例进行实验。将遗传算法，差分进化算法和混合变邻域的改进差分进化算法分别命名为GA、DE、IDDE-VNS，重复运行20次，对比3种算法的迭代曲线和优化结果。

3种算法的种群规模、迭代次数和小车数量都设为：P=80，Gmax=200，Nagv=2；GA的交叉概率和变异概率设为：Pc=0.8，Pm=0.4；DE的变异概率和交叉概率设为：F=0.7，Cr=0.5；IDDE-VNS的变异概率、交叉概率和初始退火温度设为：F=0.7，Cr=0.5，T0=20。

3种算法的搜索过程曲线如图7所示，红色实线为GA，蓝色虚线为DE，黄色点划线为IDDE-VNS。由收敛曲线图可知，GA能快速收敛到一个较优解，但易陷入局部最优；DE在进化前期较GA收敛得慢，但在搜索后期发现更优解的可能性更大，使搜索最终得到更好的解；改进后的IDDE-VNS的收敛速度在GA和DE之间，在进化后期，由于引入了变邻域搜索算法增强了DE算法的局部搜索能力，使其最终搜索到的解的质量在3种算法中最好。

图7 3种算法收敛曲线对比Fig. 7 Comparison of convergence curves of three algorithms

3种算法计算EX11算例的优化结果如表3所示，采用GA进行实验20次，得到的最优解的平均值为100.5，搜索到全局最优解96的概率为5%；采用DE进行实验20次，得到的最优解的平均值为98.5，搜索到全局最优解96的概率为10%；采用IDDE-VNS进行实验20次，得到的最优解的平均值为97.1，搜索到全局最优解96的概率为35%。由此可得，3种算法搜索到的解的质量和稳定性的关系为IDDE-VNS>DE>GA。

表3 3种算法求解EX11算例实验结果

综上所述，IDDE-VNS比GA、DE的稳定性和寻优能力更好，证明了文中提出的改进方法是有效可行的。

3.2 非柔性算例实验

Bilge等[2]提出了82个算例用来测试算法的有效性，由装载台、卸载台、4台加工机器和2台AGV构成的4种不同布局和10个不同的工件集组成。EX后面的数字中第一个表示工件集编号，第二个表示布局编号，如“EX32”表示工件集3-布局2。为了验证IDDE-VNS相比其他算法的优越性，选取其中一部分算例进行了测试。IDDE-VNS算法的控制参数设置为：种群规模P=80，最大迭代次数Gmax=500，变异概率F=0.7，交叉概率Cr=0.5，初始退火温度T0=20，小车数量Nagv=2。

每个算例独立计算20次取最优值，与其他文献得到的最优解进行对比，如表4所示。其中STW表示文献[2]采用滑动时间窗求得的最优解，AGA表示文献[3]采用遗传算法混合启发式方法求得的最优解，FDE表示文献[9]采用差分进化算法求得的最优解，FMAS表示文献[19]采用基于MAS方法求得的最优解。

由表4可知，IDDE-VNS算法计算测试算例时，其中100%的解优于或等于STW和AGA的实验结果；85%的解优于或等于FDE的实验结果；90%的解优于或等于FMAS的实验结果。特别地，IDDE-VNS算法计算EX71和EX92的解在对比实验中结果最好。由此可看出，IDDE-VNS在计算机器与AGV同时调度问题时表现优秀，与其他优秀算法相比有较高的搜索质量，证明了IDDE-VNS算法的优越性。

表4 非柔性算例实验结果

3.3 柔性算例实验

上述算例中工件的每道工序可选择的加工机器是唯一的，没有体现生产系统的柔性。在FMS中，不同加工机器的选择会影响AGV路线的选择，从而影响AGV的空载时间和负载时间以及工序的开工时间和完工时间。为了更好体现IDDE-VNS算法在FMS中的作用，借鉴Zhang等[10]给出的柔性作业车间集成调度算例，由6个工件、6台机器和4台AGV构成。

IDDE-VNS算法的控制参数设置与非柔性算例实验一致，其中最大迭代次数与文献[10]一致，小车数量改为Nagv=4，运行10次取最优值，最优实验结果的调度甘特图见图8，最大完工时间为75.6 min。对比Zhang等[10]采用改进粒子群优化算法得到的最大完工时间85 min，IDDE-VNS算法搜索到的解的质量更好，证明了IDDE-VNS算法求解FMS中机器与AGV同时调度问题的优越性。