圆环非线性隔振设计和动力学研究

顾栋浩，陆泽琦，丁 虎，陈立群

（1.上海大学上海市应用数学和力学研究所，上海200072；2.上海大学力学在能源工程中的利用重点实验室，上海200072；3.上海大学力学与工程科学学院，上海200072）

引言

传统线性隔振系统只有在激励频率大于系统固有频率的2倍时才能有效。因此，尽可能降低隔振系统的固有频率，可以显著提高低频隔振效果。考虑工程应用、制作成本等因素的限制，传统线性隔振系统很难通过降低有效刚度和增大隔振器质量来实现低频隔振。因此，利用非线性特性来提高隔振系统的性能，是一种有前景的振动控制方式。

弹性曲梁、弹性环、轴向移动梁、弹性曲板等弹性元件往往具有特殊形状结构的力与变形的非线性关系［1］，对实现低频隔振具有重要意义。屈曲荷载和后屈曲行为对结构设计具有重要意义，例如，将弹性环的屈曲状态作为静平衡状态时，设计了弹性环低频隔振器，从而降低了动态刚度［2］。

圆环的屈曲和后屈曲变形是Love提出的经典问题，主要研究圆环面内和面外弯曲的平衡和稳定性［3］。Love的研究引起了许多学者的关注，他们利用多种理论，尝试解决圆环的大变形问题。Wu等［4］研究了在一些平衡点附近弯曲和扭转弯曲环的弹性稳定性。Tse等［5］研究了正交各向异性对称圆环非线性弹性行为，推导了力与位移的关系。Wu等［6］运用牛顿法和谐波平衡法，得出了圆环大变形的近似解析解。上述研究主要集中在静力作用下圆环的平衡位置、稳定性和挠曲等方面问题。Lacarbonara等［7］在考虑材料非线性行为的影响下，研究了圆环在自由状态下的非线性振动。Xu等［8］从理论上研究了功能梯度（FGM）环的自由振动，导出了FGM环自由振动的频率方程，考察了静平衡时的动刚度特性，得出了静载质量引起的静平衡偏差对隔振器的失稳有重要影响的结论。Liu等［9］通过在平衡位置处引入预变形欧拉屈曲梁来提供负刚度，抵消正刚度，降低隔振器的整体动刚度，并优化梁的结构参数提高隔振性能。Huang等［10］利用欧拉屈曲梁作为负刚度修正器，研究了非线性隔振器的隔振特性。Ding等［11］研究了具有垂直弹性支承边界的黏弹性梁的振动。

此外，在平衡点附近的动态刚度特性是设计非线性隔振系统的关键因素。虽然，Lacarbonara等［12］论述了弹性绳索、三维实体、弯曲梁和板的静态和动态特性。然而，研究仅限于对它们的振动分析，还没有利用弯曲弹性体以提高隔振性能的研究。

由于高静态低动态刚度能改善低频隔振性能，同时不产生较大的静态变形，近年来被广泛采用［13］。实现高静态低动态刚度的一种简单方法是三弹簧结构非线性隔振器，即利用两个水平预压的弹簧和一个竖直弹簧构成隔振系统，系统在振动过程中由于几何关系产生非线性刚度［14-15］。实现这一特性还有其他许多方法，见参考文献［16-19］。此外，可以通过使用非线性阻尼元件来改进线性隔振系统，特别是为了在共振时抑制响应和在高频时保持良好隔振性能［20-23］。与垂直阻尼相比，水平阻尼具有一些优势，其隔振效果已与垂直线性弹簧结合考虑［24-25］。

本文的目的是研究如何将水平刚度和阻尼有效地应用于环形梁隔振系统中。其目的是将非线性刚度和非线性阻尼结合起来，综合两种结构的优点，提高隔振的频率范围，同时改善共振抑制和高频隔振。将直接分离运动法用于推导所研究隔振器的位移传递率［26-27］，并比较解析与数值结果。

1 系统建模

图1所示为一个添加水平弹簧和水平阻尼的圆环隔振系统，圆环上端是质量为m的水平平台，下端固定在底座上，圆环的半径为R，厚度为H，宽度为W，水平放置的弹簧kh和水平阻尼ch通过几何变形使得整个圆环隔振系统产生非线性刚度和非线性阻尼。底座受到位移激励xe的作用，研究非线性刚度和非线性阻尼的变化对位移传递率的影响，以此来评价隔振系统的性能。

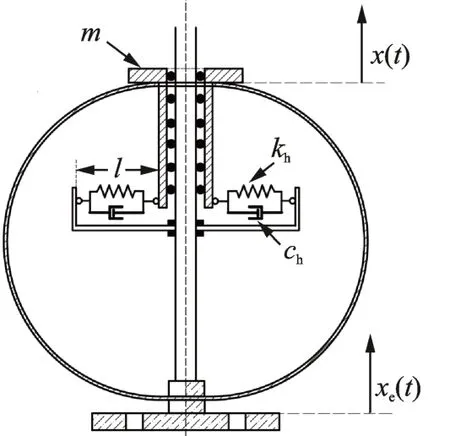
图1 非线性刚度、非线性阻尼的圆环隔振器示意图Fig.1 Schematic of a circle ring isolator combined with nonlinear stiffness and damping

根据圆环结构的非线性特性，圆环在受到水平平台预压的前提下，在静平衡位置力与位移的关系式可表示为

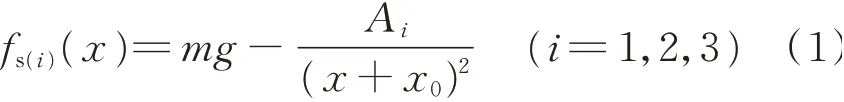
式中x0表示在预受压状态下圆环的静变形，x表示离平衡位置的位移，Ai表示圆环力与位移的关系在受压过程中三个不同变形阶段的参数［5］。

圆环受压阶段1：

圆环受压阶段2：

圆环受压阶段3：

式中φB=sin-1(1/p2)，E22表示杨氏模量，I表示惯性矩，E（p，φB）和F（p，φB）分别表示第一类不完全椭圆积分和第二类不完全椭圆积分，p=表示构 造圆弧 半径［5］，在位移激励xe=Xecosωt作用下，系统的运动方程可写为

式中xr=x-xe表示水平平台与底座间的相对位移，Xe和ω分别表示位移激励的振幅和激励频率。c表示圆环自身阻尼，cn表示由水平阻尼产生的非线性 阻 尼 项表 示 由 水 平弹簧产生的非线性刚度项，kn=2kh[1-l0(x2+l2)12]，l表示弹簧在水平位置的长度，如图1所示。l0表示水平弹簧的自由长度，当位移很小时，非线性阻尼项和非线性刚度项可分别简化为

2 位移传递率

2.1 直接运动分离法

利用直接运动分离法，研究系统的位移传递率，令方程（5）解的形式为

式中新的时间尺度T0=ωt，T1=εT0。ε表示小参量，α表示慢变量，ψ表示快变量，ψ(T1，T0)=0，将快慢运动分离得到：

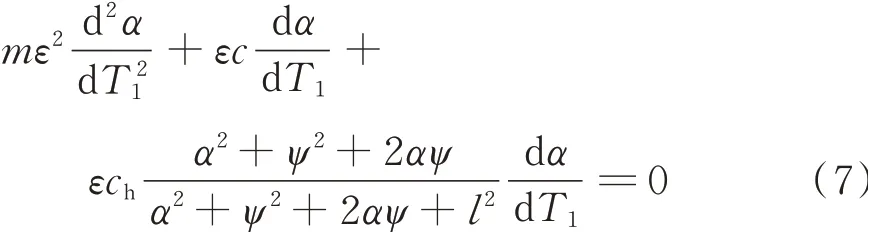
考虑到ψ(T1，T0)是时间T0的周期函数，方程（8）的解可以设为

忽略含B2和θ2的项及更高次项，将式（9）代入式（8）可得：

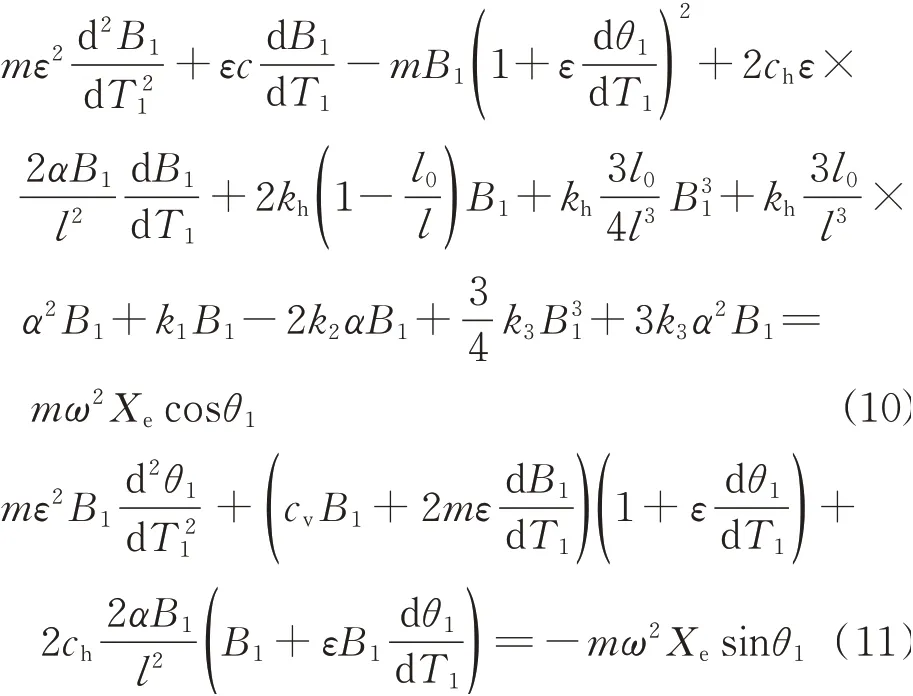
式中k1=2Ai/x30，k2=3Ai/x40，k3=4Ai/x50。

稳定状态下，慢变运动方程可得

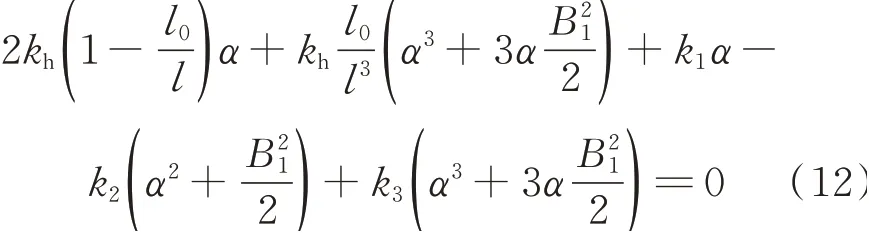
快变运动方程可得：

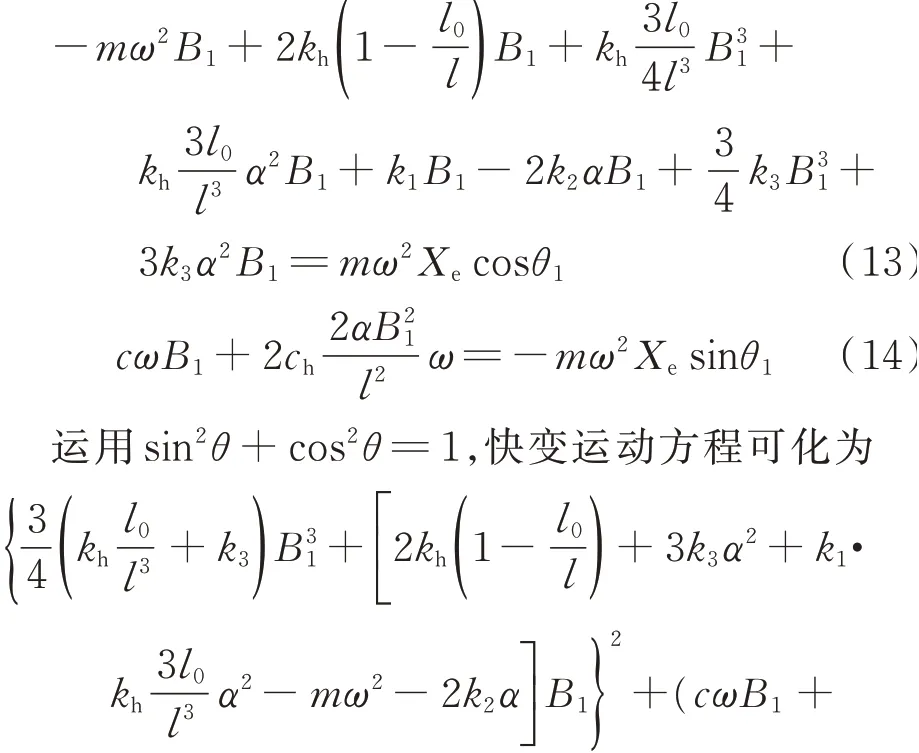
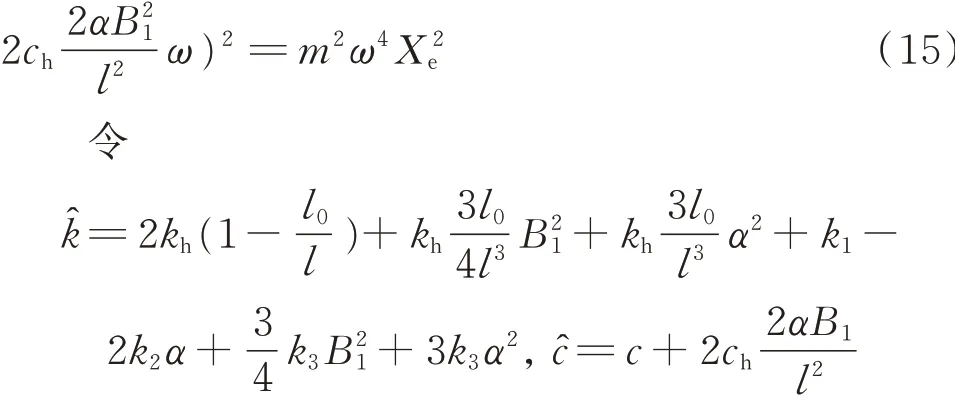
由方程（15）得出稳态激励频率解

由系统的相频关系可以得到

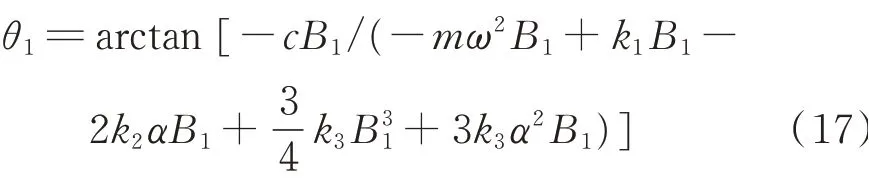
隔振器的位移传递率表达式可表示为

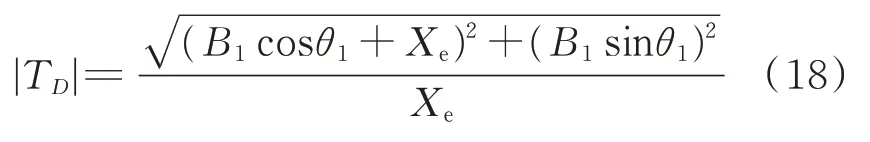
2.2 数值验证

圆环隔振器的物理和几何结构基本参数选取如表1所示，隔振系统参数如表2所示。在下面的案例分析中如果没有特殊说明将采用表1和表2中的参数值。

表1 圆环的物理和几何参数值Tab.1 Physical and geometrical properties of the ring

表2 隔振系统参数值Tab.2 Parameters of the vibration isolation system

圆环在质量m=0.20 kg作用下达到预屈曲阶段1，k1=2.04 kN/m，k2=3.19×102kN/m，k3=4.43×104kN/m，令水平刚度kh=800 kN/m，水平阻尼cn=0.3 N·s/m，如图2点划线所示。在质量m=2.04 kg作用下达到预屈曲阶段2，k1=0.165 kN/m，k2=2.09 kN/m，k3=23.44 kN/m，令水平刚度kh=80 kN/m，水平阻尼cn=0.3 N·s/m，如图2虚线所示。在质量m=5.10 kg作用下达到预屈曲阶段3，k1=0.051 kN/m，k2=0.204 kN/m，k3=0.72 kN/m，令水平刚度kh=20 kN/m，水平阻尼cn=0.3 N·s/m，如图2实线所示。图2中位移传递率小于1的部分为有效隔振区域。

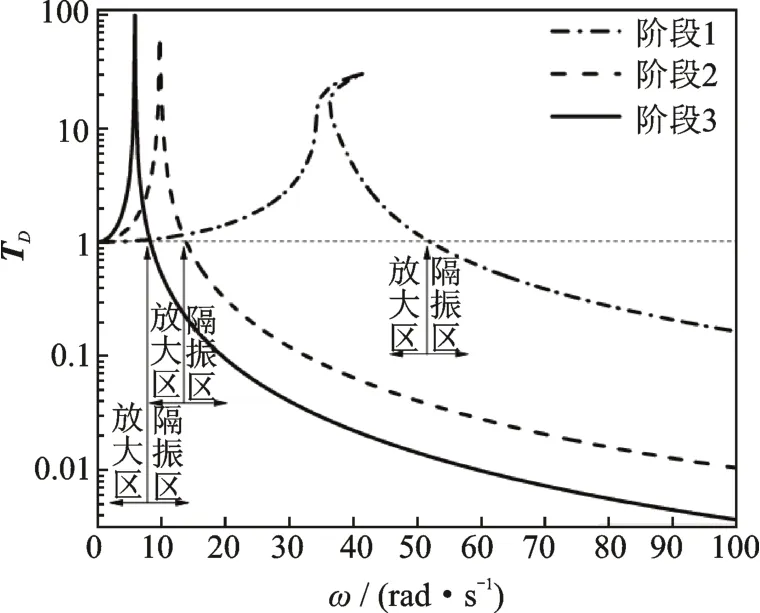
图2 含有水平刚度阻尼圆环隔振器的位移传递率Fig.2 Displacement transmissibility with horizontal stiffness and horizontal damping in three stages

采用四阶龙格库塔法对圆环隔振器的位移传递率解析结果进行数值验证，三个阶段的解析结果和数值结果对比如图3所示，两者吻合良好。说明直接运动分离法能很好地捕捉非线性圆环隔振的动力学特性。

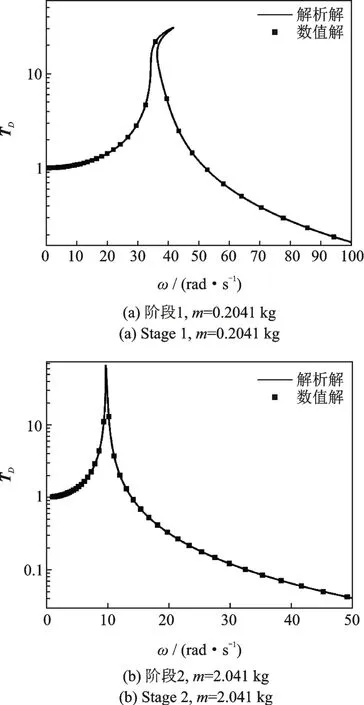
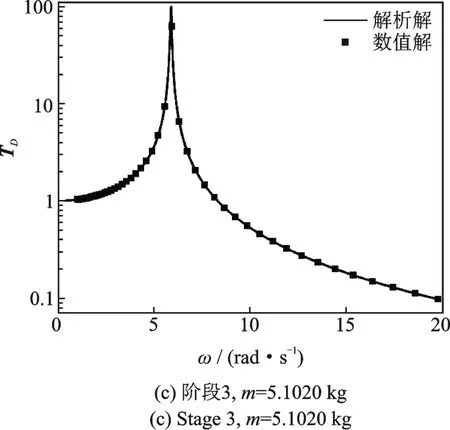
图3 含有水平刚度阻尼圆环隔振器的位移传递率数值结果与解析结果对比Fig.3 Comparisons between numerical and analytical results of displacement transmissibility of circular ring isolators with horizontal stiffness and damping

在阶段3时，对比研究了含有水平弹簧和不含有水平弹簧的圆环隔振器位移传递率，如图4所示，圆环隔振器加上水平弹簧后，隔振频率频带往低频拓展。三个阶段圆环刚度依次减小，因此，为了不出现负刚度，三个压缩阶段水平刚度最大取值也应该依次减小。水平刚度的引入是为了减小系统总刚度，进一步提高隔振带宽。

图4 在阶段3时，含有水平弹簧和不含有水平弹簧的圆环隔振器位移传递率对比Fig.4 Comparison of the displacement transmissibility between with and without horizontal stiffness for stage 3

3 参数研究

研究了非线性刚度和非线性阻尼分别对圆环隔振器的影响，从动力学方程（5）中可以看出，水平非线性刚度kn和水平非线性阻尼cn的变化影响隔振性能。

首先，考虑水平刚度的影响，令水平非线性阻尼cn=0，在不同屈曲状态，水平刚度系数选择如图5所示，可以看出随着受压屈曲变形增大，圆环隔振器的整体共振频率下降，同时在单一受压平衡状态随着水平刚度的增加，位移传递率的峰值减小，共振频率值减小，系统隔振频带变宽，在高频处，位移传递率曲线会逐渐翘起，隔振性能逐渐恶化。

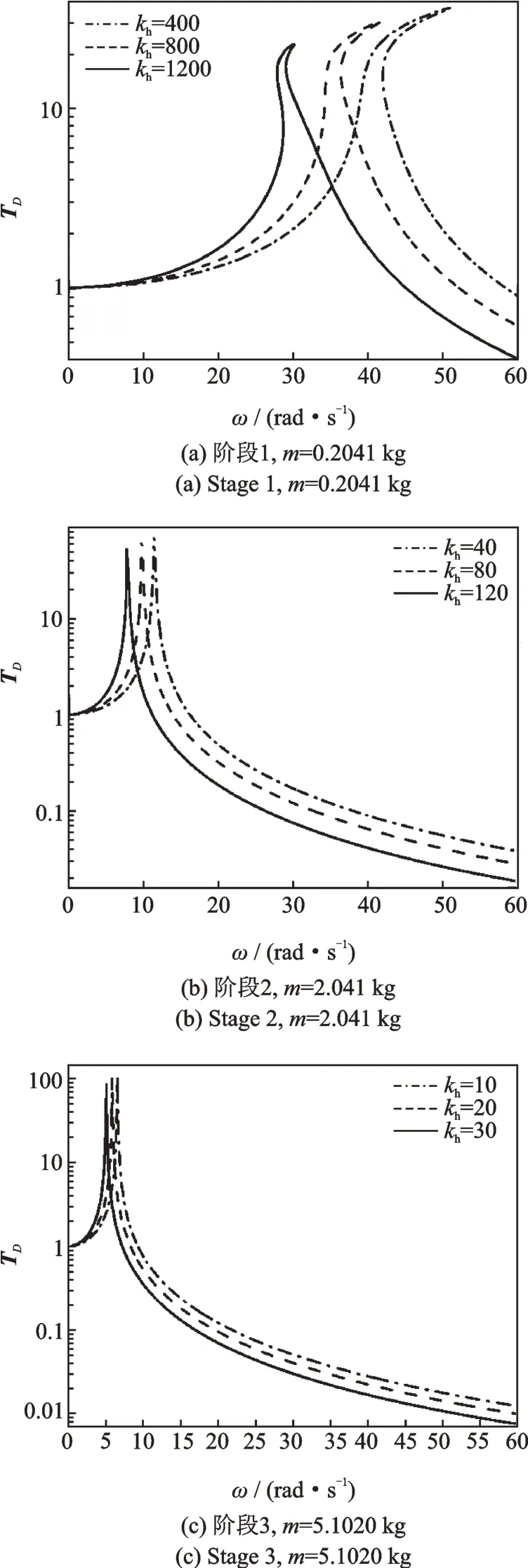
图5 刚度变化对圆环隔振器不同阶段的影响Fig.5 Displacement transmissibility of the isolator with horizontal stiffness in three stages for different stiffness coefficients

考虑水平阻尼对圆环隔振器的影响，令第一阶段kh=1200 kN/m，m=0.2041 kg；第二阶段kh=120 kN/m，m=2.041 kg；第三阶段kh=30 kN/m，m=5.102 kg。阻尼系数变化分别为0.3，30，300 N·s/m。得到响应的位移传递率如图6和图7所示。可以看出，随着水平阻尼的增加，位移传递率的峰值减小，同时降低了隔振的初始频率，也就意味着拓宽了隔振频带。与图5相比较，阻尼系数的改变对拓宽隔振频带的能力不如刚度系数的变化，但是，在隔振频域，水平阻尼不损害隔振器高频隔振表现。因此，添加水平阻尼能够很好地抑制共振峰值，同时在高频隔振能够表现很好。

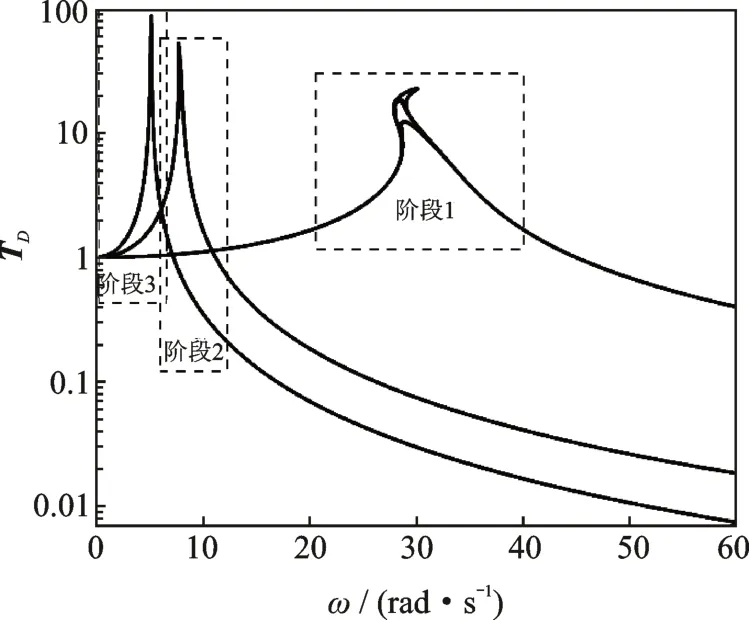
图6 在三个阶段水平阻尼对位移传递率的影响总图Fig.6 Effects of horizontal damping on the displacement transmissibility in three stages

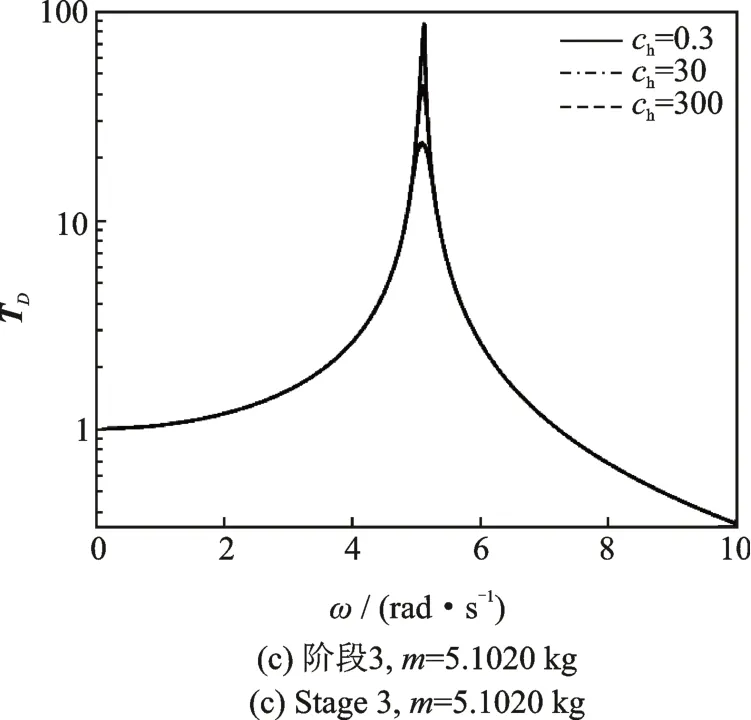
图7 水平阻尼对位移传递率各个阶段影响图Fig.7 Effects of horizontal damping on the displacement transmissibility in three stages for different damping coefficients

4 结论

针对圆环隔振系统，添加水平弹簧和阻尼产生非线性刚度和阻尼来实现低频隔振。利用圆环自身的静力学特性，将圆环隔振研究分为三个阶段。运用直接运动分离法分析动力学方程，从而得到位移传递率，来评价隔振器性能。对位移传递率的解析结果进行数值验证，两者吻合良好。在此基础上，研究了水平刚度和阻尼对位移传递率的影响。结论如下：（1）水平刚度能够减小共振频率，拓宽隔振频带，有效抑制共振响应；（2）水平阻尼能有效抑制共振，不改变系统的共振频率，具有较好的高频隔振表现；（3）同时利用水平阻尼和水平刚度能够获得更好的隔振性能。