高阶非线性刚度的调谐质量阻尼器控制性能分析

孙 毅，李芦钰

（大连理工大学建设工程学部智能结构系统研究所，辽宁大连116024）

引言

调谐质量阻尼器由于其具有结构简单、无需耗能、稳定性好等优点，在土木工程结构振动控制方面得到了广泛的应用［1-4］。例如美国波士顿的John Hancock大楼、澳大利亚的悉尼电视塔和日本明石海峡大桥的桥塔上均安装了TMD装置［5］，这些TMD装置成功抑制了结构在地震荷载和风荷载作用下产生的动态响应。然而，在实际应用过程中，TMD由于其过大的位移或者限位装置的应用而表现出非线性特性［6-7］。因此，研究非线性调谐质量阻尼器（NTMD）的控制性能具有实际的工程意义。

近些年来，关于NTMD的研究已经取得了极大的进展。作为NTMD的一种形式，非线性能量阱（Nonlinear Energy Sinks，NES）得 到 了 广 泛 的 研究［8-10］。相较于线性TMD，NES能够与结构的任意阶模态产生共振现象，因此具有更宽的有效控制频率范围［11-14］。此外，NES能够从低阶模态到高阶模态分配结构的输入能量，并且使得能量从结构到NES单向、不可逆地传递，进而抑制结构的振动［15］。但是，非线性TMD也存在不稳定现象及结构响应幅 值 被 放 大 的 问 题［16-17］。Alexarder等［18］和Djemal等［19］通过实验，证明了非线性TMD存在跳跃现象。Alexarder等［18］指出，只有消除或减小非线性TMD产生的高幅值周期解，系统的稳态响应才会优于线性TMD控制下系统的稳态响应。为了消除高幅值的周期解，Starosvetsky等［20］提出了半主动的分段二次黏性阻尼器。数值分析表明，这种阻尼器能够消除被分离的高幅值周期解。此外，Eason［21］通过在NTMD系统上附加一个可调刚度的单摆，同样能够有效地消除共存的高幅值周期解。

在NTMD参数优化方面，一些学者根据不同的性能指标和优化方法对NTMD参数优化做了研究。其中Habib等［22］利用Den Hartog的等峰值方法研究了NTMD的参数优化问题，并给出了参数优化的解析 形式。Fallahpasand等［23］对非 线 性 单 摆 式TMD的控制性能进行了分析，利用H∞和H2方法对TMD进行参数优化，得到了TMD设计的最优参数值。陈勇等［24］进行了基于NES的高耸结构减振分析，获得了非线性模态的解析解，并给出最优参数计算的经验公式。

本文考虑TMD的五次刚度非线性对结构的控制性能进行分析，并结合Li等［25］提出的NTMD改进的设计方法，提出一种适用于五次非线性刚度的NTMD的改进设计方法。然后，利用该方法对NTMD进行设计修正，并根据数值模拟的结果验证了所提出的改进设计方法的有效性。

1 NTMD理论分析

1.1 系统运动方程

本文以有阻尼受迫振动为例，系统运动模型如图1所示。可见，系统由线性主结构与耦合非线性TMD两部分组成。其中非线性TMD的形式为五次刚度非线性，其力-位移关系可表示为Fd=k21x-k22x3+k23x5，其中k21为线性刚度系数，k22为三次软化刚度系数，k23为五次硬化刚度系数，且以上刚度系数均大于零。系统的运动方程可表示如下：

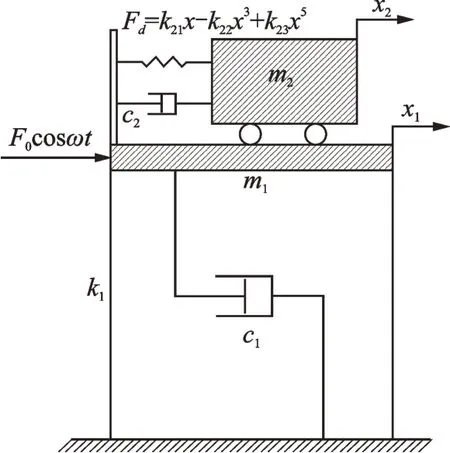
图1 系统受迫运动示意图Fig.1 Schematic diagram of forced movement of the system

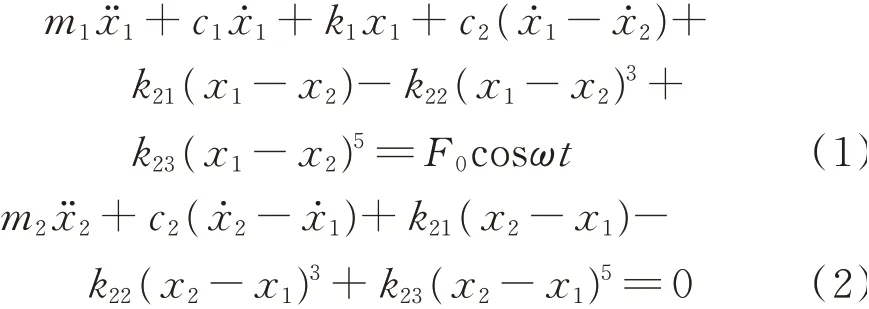
式中m1，c1，k1，x1分别为结构的质量、阻尼、刚度和绝对位移；m2，c2，k21，x2分别为NTMD的质量、阻尼、线性刚度和绝对位移；系统的输入假设为正弦激励即u(t)=F0cosωt，其中F0为激励幅值，ω为激励频率。

由方程（1），（2）可知，直接对系统的运动方程进行分析是非常困难的，为了将NTMD的分析从整个系统分离出来，可以认为在正弦激励作用下，当系统的非线性较弱时，主结构的稳态响应可近似为一阶谐响应x1=Acos(ωt+β)。在分析的过程中，忽略相角的影响，仅考虑稳态响应。则NTMD的运动方程可表示为

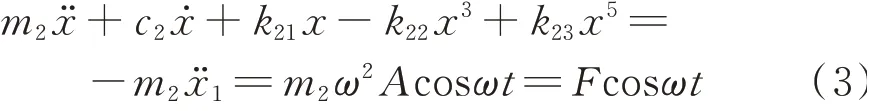
式中x=x2-x1为NTMD相对于主结构的位移；A为主结构的稳态振幅；F为NTMD的等效激励幅值；ω为相应的激励圆频率，本文在设计过程中取ω为主结构的第一阶固有频率。

为了分析方便，引入无量纲参数：

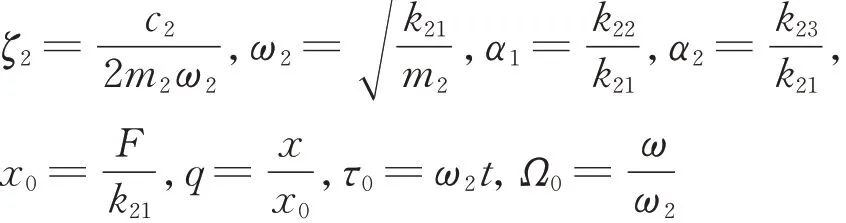
则NTMD的运动方程可表示为无量纲形式

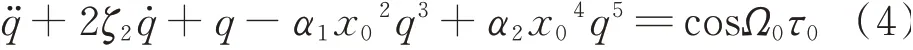
式 中q̈表示ζ2和ω2分别为非线性TMD的阻尼比和线性频率；α1和α2分别为NTMD的软化非线性系数和硬化非线性系数；x0为NTMD的等效静位移；q，τ0和Ω0分别为NTMD的无量纲位移、无量纲时间和无量纲频率。

1.2 方程的近似解析解

本文采用平均化方法［26］求解NTMD的运动方程，假设TMD的位移响应为一阶谐波响应，响应频率为激励频率，即：

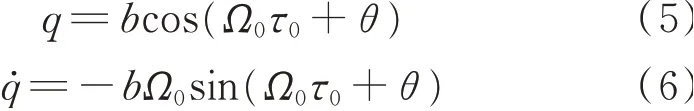
式中b为响应幅值；θ为对应相角。

将式（5）和（6）代入方程（4）中，得到：

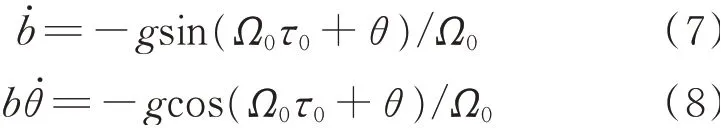
对于稳态响应，响应幅值和相角随着时间缓慢变化，方程（7）和方程（8）可以近似表示为一个周期内的积分均值，即：

对方程（9）和方程（10）在一个周期内积分平均可得：

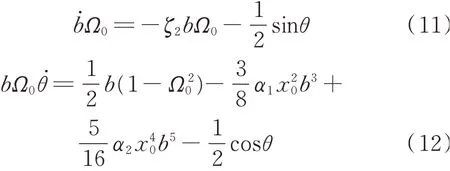
对于稳态响应，有ḃ=θ̇=0，消去方程（11）和方程（12）中的正弦项和余弦项，得到NTMD的频响曲线方程

1.3 NTMD的幅频关系分析

由频响曲线方程可知，在确定的激励频率作用下，NTMD的响应幅值与阻尼比ζ2、非线性系数α1，α2和等效净位移x0有关，表现在频响曲线中如图2所示。随着阻尼比ζ2的增大，NTMD的最大响应幅值在减小，幅频响应曲线向右偏移的程度减轻，非线性的影响越来越小；当固定软化非线性系数α1，随着硬化非线性系数α2的增大，幅频响应曲线由向左偏移渐渐转变为向右偏移，非线性的影响由软化非线性效应转变为硬化非线性效应；当等效净位移x0增大，幅频响应曲线向右偏移，NTMD的最大响应幅值在减小，非线性的影响越来越大。

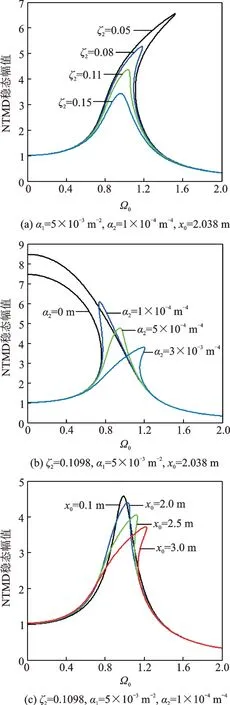
图2 非线性TMD频率响应曲线Fig.2 Frequency response curve of nonlinear TMD

以硬化非线性效应下NTMD的幅频响应为例。如图3所示，从图中可以看出，NTMD幅频响应曲线存在多幅值解现象。稳定性分析表明，位于多幅值解区域的中间曲线是不稳定的，在实际中并不会出现。此外，NTMD幅值响应存在跳跃现象，图中点A和点B为跳跃点，在跳跃点处，响应幅值会突然增大或减小。在多幅值解区域，系统的响应取决于该区域的初始条件。如果初始条件为0或者很小，跳跃现象将发生在点A；如果初始条件较大，跳跃现象将发生在点B。因此当初始条件一定的情况下，NTMD在跳跃点处具有最大的响应幅值。考虑到实际工程中，多数的结构处于静止状态，且风荷载的频率变化较小，因此，可以认为跳跃现象发生在点A且此时NTMD的响应幅值为最大。

2 跳跃频率求解

通过以上分析可知，在跳跃点处NTMD具有最大的位移响应，NTMD的最大位移响应对应最好的控制效果［25］。因此，新的分析设计方法将依据跳跃点处的频率对NTMD进行设计修正，首先应求解跳跃点处的频率。在跳跃点处，频率响应曲线具有垂直的切线，若将跳跃频率Ω0看成NTMD位移响应b的函数，即Ω0=Ω0(b)，则在跳跃点处有如下关系将频响曲线方程（13）两边对b求导，得

当阻尼比ζ2较小时，近似地有此时λ可近似为

利用二次方程的求根公式解方程（16），得

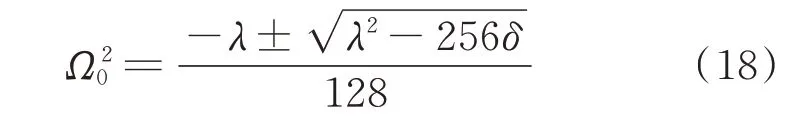
可以发现二次方程（16）有以下两个实根：

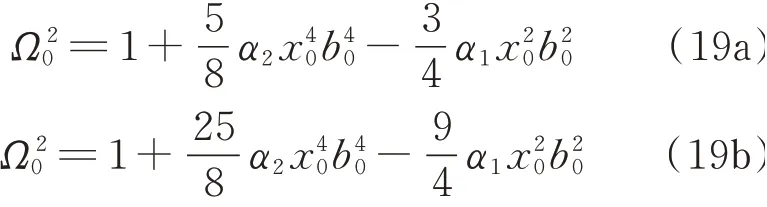
由伽罗瓦可解性判定准则可知五次及以上方程没有固定的根式解，因此考虑用渐进展开式求得五次方程的近似解。

当ε≈0时，式（23）可简化为

仅考虑实根，假定展开式

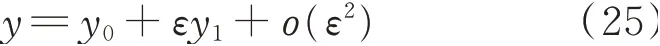
将展开式代入式（24），并使ε同次幂的系数等于零，可以得出：

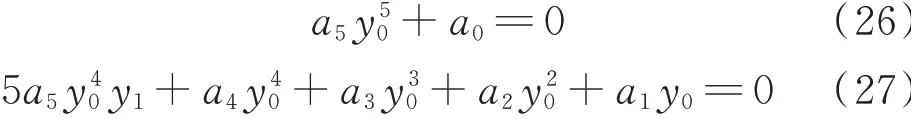
因此：

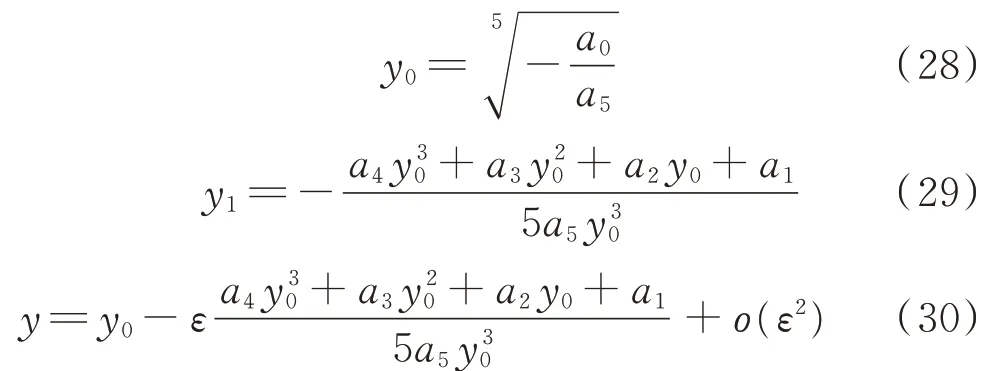
通过上述过程，得到了跳跃点频率的近似解析解，表1和2分别计算了不同静位移x0和不同非线性系数α2下的跳跃频率，通过对比可以发现近似解析解与数值解非常接近，且最大误差不超过5%，说明近似解析解具有足够的精度。

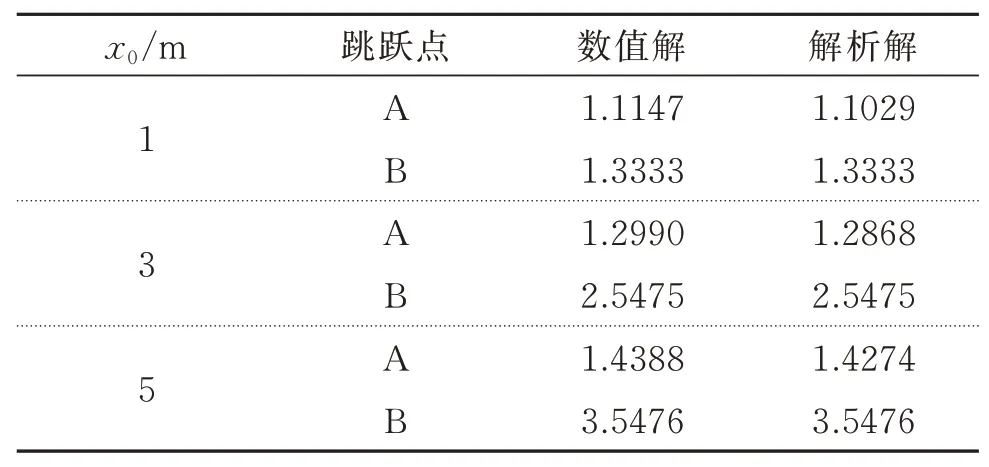
表1 跳跃频率的数值解与解析解(ζ2=0.05，α1=5×10-3 m-2，α2=5×10-4 m-4)Tab.1 Numerical and analytical solutions of jump frequency(ζ2=0.05，α1=5×10-3 m-2，α2=5×10-4 m-4)

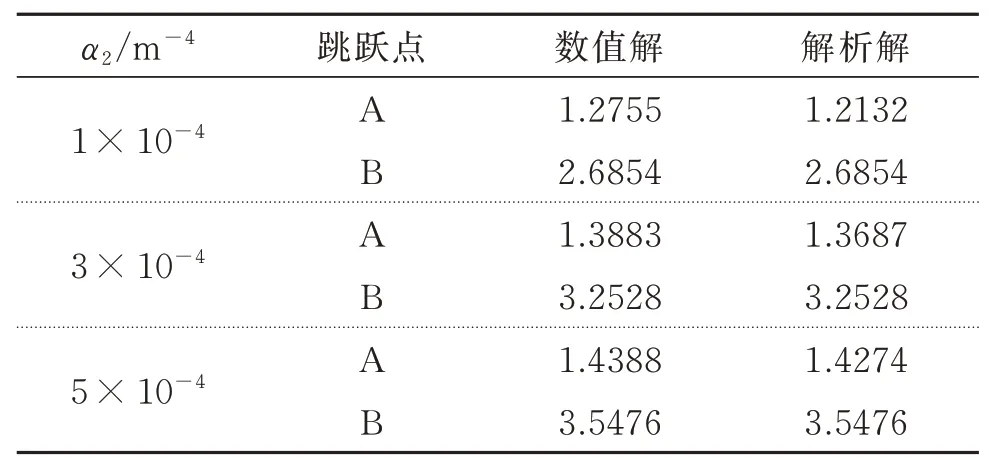
表2 跳跃频率的数值解与解析解(ζ2=0.05，α1=5×10-3 m-2，x0=5 m)Tab.2 Numerical and analytical solutions of jump frequency(ζ2=0.05，α1=5×10-3 m-2，x0=5 m)

另外，在计算跳跃频率解析解的过程中，忽略了阻尼比的影响，通过对比解析解与数值解的差异（见表1和2），可以认为这种假设是合理的。考虑到在0初始条件或较小的初始条件下，跳跃现象发生在A点，因此仅分析阻尼比对A点的跳跃频率解析解的影响。当非线性系数α1，α2和等效净位移x0保持不变时，分别取不同的阻尼比计算NTMD跳跃频率的解析解。从表3可以看出，阻尼比从0变化到0.15，解析解变化小于0.03。所以，在小范围内改变阻尼比的情况下，A点的跳跃频率解析解可以视为不变。在研究阻尼比变化对于控制性能的影响时可以忽略阻尼比变化带来的误差，将其视为独立的变量。

表3 阻尼比对A点跳跃频率的影响(α1=5×10-3 m-2，α2=5×10-4 m-4，x0=5 m)Tab.3 Influence of damping ratio on jump frequency at point A(α1=5×10-3 m-2，α2=5×10-4 m-4，x0=5 m)

3 NTMD设计方法

考虑五次刚度条件下NTMD可能产生的先软化后硬化的非线性行为，在设计NTMD的过程中，对传统的线性TMD设计方法进行修正，以减小NTMD在使用过程中非线性行为的不利影响。当TMD的位移响应最大时，TMD提供的弹簧力最大，相应的结构位移响应越小，TMD的控制效果越好［21］。因此，TMD的参数优化基于TMD的最大位移响应。已知NTMD在跳跃点A处有最大的位移响应，因此根据A点的跳跃频率进行NTMD的参数优化设计。

参考无量纲化的过程可知，A点的跳跃频率Ω0A=ω/ω2，结合式（31）则有

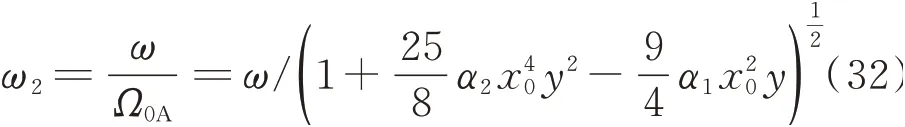
式中ω2为NTMD的最优设计频率，此时NTMD具有最好的控制效果。当激励频率与结构频率相同即共振条件下，NTMD与结构的最优频率比为

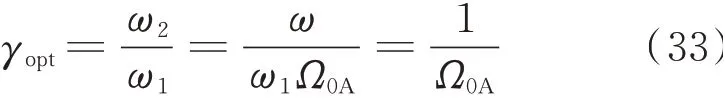
从式（33）可以看出，NTMD的最优频率比与跳跃频率互为倒数关系，且仅与参数α1，α2，ζ2，x0有关。经过参数优化后要求设计前后的跳跃频率是不变的，因此这里通过调整NTMD的质量来满足其最优设计频率，即

由此，在传统线性TMD的设计基础上通过修正NTMD的质量来减小NTMD非线性行为的不利影响。对于硬化非线性效应下的NTMD，其跳跃频率总是大于1的，因此最优频率比小于1，经过参数优化后NTMD的质量增大。下面通过计算一个实例以验证改进设计的控制效果。

4 NTMD控制性能

4.1 设计算例

以单自由度结构为例，结构的参数为m1=1 kg，c1=0.1 N•s/m，k1=1 N/m，结构采用余弦激励，其幅值为F0=0.5 N，激励频率为ω。取质量比μ=0.05，按照线性TMD方法进行设计［27］，计算得最优频率比γopt=0.9404，最优阻尼比ζopt=0.1098。因此，TMD的参数为：m2=0.05 kg，c2=0.0103 N•s/m，k21=0.0442 N/m，k22=k23=0。由于调谐质量阻尼器在实际应用的过程中产生的非线性行为，假设非线性系数α1=5×10-3m-2，α2=5×10-4m-4。则NTMD的 实 际 参 数 为：m2=0.05 kg，c2=0.0103 N•s/m，k21=0.0442 N/m，k22=2.21×10-4N/m3，k23=2.21×10-5N/m5。实 际 弹簧的非线性本构方程根据实际测量的结果确定，这里仅假设一种形式。

当考虑非线性时，TMD的控制效果将发生变化，如图4所示。从图中可以看出，产生非线性效应后TMD的控制效果在结构共振频率附近被恶化。当非线性系数α2=0，结构处于软化非线性效应时，在频率小于1范围内NTMD控制效果优于线性TMD，但是在频率大于1范围内TMD的控制效果变差；当非线性系数α2=5×10-4m-4，结构处于硬化非线性效应时，在频率大于1范围内NTMD控制效果优于线性TMD，但是在频率小于1的范围内对结构的控制效果严重恶化，结构响应幅值显著增大。

图4 TMD的非线性行为对控制性能的影响Fig.4 Influence of nonlinear behavior of TMD on control performance

针对线性TMD产生非线性效应后的不利影响，下面按照NTMD参数优化方法对NTMD进行改进设计。为了设计NTMD参数，等效激励幅值需要被确定。已知等效激励幅值F=m2ω2A，其中，A为结构响应幅值，ω为结构响应频率。考虑在共振条件下，此时ω=1 rad/s，结构稳态响应幅值A=1.7464 m，则等效激励幅值F=0.0873 N。计算跳跃频率所需的四个参数值分别为：ζ2=0.1098，α1=5×10-3m-2，α2=5×10-4m-4，x0=F/k21=1.9748 m。由公式（31）可求得跳跃频率Ω0A=1.1858，最优频率比γopt=1Ω0A=0.8433。通过调整TMD的质量来满足其最优频率比，经过修正设计后TMD的参数为：m2=0.0622 kg，c2=0.0115 N•s/m，k21=0.0442 N/m，k22=2.21×10-4N/m3，k23=2.21×10-5N/m5。

基于改进设计前后结构的频率响应曲线如图5所示：从图中可以看出，基于改进的设计方法能够获得更好的控制效果，极大地减小了结构共振频率处的响应幅值，且频率响应曲线位于左侧的峰值降低。随着激励幅值的增大，TMD的控制效果越明显。图6（a）显示了共振情况下结构位移-时程曲线，从图中可以看出，改进设计方法能够显著降低非线性因素的影响，结构位移减小了34%。图6（b）为在激励频率为1.05 rad/s时结构位移-时程曲线，由图可知，结构在频率为1.05 rad/s激励作用下响应是不稳定的，所以仿真结果会出现两个右侧峰值的现象。

图5 结构频率响应曲线Fig.5 The frequency response curve of the structure

图6 结构时程响应曲线Fig.6 The time-history response curve of the structure

4.2 阻尼比的影响

作为NTMD设计的另一个参数，阻尼比对TMD控制性能有较大的影响。图7为阻尼比变化对NTMD幅频曲线的影响，从图中可知，随着阻尼比的增大，共振频率处的结构响应幅值增大，同时过小的阻尼比在非共振频率处存在更高的峰值。所以在选择NTMD阻尼比时，要综合考虑阻尼比对控制性能的影响。因为阻尼比对于跳跃点频率的解析解影响不大，可以将其忽略。所以，在研究阻尼比变化对控制性能的影响时，可以忽略其对NTMD设计频率的影响，即在研究阻尼比变化对控制性能影响过程中把阻尼比视为独立的变量。

图7 阻尼比对非线性TMD控制性能的影响（F0=0.5 N）Fig.7 Influence of damping ratio on control performance of nonlinear TMD（F0=0.5 N）

4.3 等效幅值的影响

在对NTMD进行改进设计的过程中，要求参数α1，α2，ζ2和x0保持不变。这是因为跳跃频率Ω0A是在确定的α1，α2，ζ2和x0值的情况下计算出来的，如果发生变化，会引起跳跃频率发生变化，进而会影响到NTMD的设计频率值。在实际的设计过程中，通过 改 变NTMD质量调整NTMD的频 率，NTMD的刚度没有发生变化，因此α1，α2保持不变。由前文分析可知，小范围变化的阻尼比对于跳跃频率影响很小，可以将其影响忽略，所以ζ2也可以视为不变量。在改进设计前后，结构的稳态位移幅值不同，必然会引起等效激励幅值F随之改变，相应的等效静位移x0发生变化。从表4可以看出，当激励幅值不超过0.5 N时，设计前后等效静位移变化在0.5 m范围内，跳跃频率变化较小；当激励幅值超过0.5 N时，设计前后等效静位移变化增大，跳跃频率变化明显。所以，在激励幅值较小时，设计前后等效静位移x0可以视为不变量。

表4 设计前后等效位移幅值和跳跃频率的变化Tab.4 The change of equivalent displacement amplitude and jump frequency before and after design

5 结论

线性TMD由于位移过大或限位装置应用等会产生非线性效应，在考虑非线性弹簧引起非线性刚度的条件下，当TMD处于硬化非线性状态时，TMD的控制性能在频率小于或等于1范围的内被恶化，对结构的控制产生不利的影响。针对线性TMD实际应用中可能产生非线性效应的问题，本文采用新的NTMD分析设计方法在TMD设计过程中对其进行设计修正。结果表明，经过设计修正的NTMD能够降低五次刚度非线性效应的影响，共振频率处的响应幅值和频率小于1范围内幅频曲线的峰值显著降低。当激励荷载F0=0.5 N时，共振条件下结构的位移减小了34%。

阻尼比较小时，其对跳跃点频率解析解影响较小，当阻尼比在较小范围内变化时，阻尼比的变化对跳跃点频率解析解影响可以忽略。阻尼比从0变化到0.15，跳跃点频率值变化小于0.03。所以，在研究阻尼比对NTMD控制性能影响时，不考虑阻尼比变化引起NTMD设计频率值的变化，将阻尼比视为独立变量。随着阻尼比的增大，共振频率处的结构响应幅值增大，非共振频率处的峰值降低，因此在选择NTMD阻尼比时，要综合考虑阻尼比对控制性能的影响。

当激励幅值不超过0.5 N时，设计前后等效静位移变化在0.5 m范围内，跳跃频率变化较小；当激励幅值超过0.5 N时，设计前后等效静位移变化变大，跳跃频率变化明显。所以，在激励幅值较小时，设计前后等效静位移x0可以视为不变量。