线形-拱形组合梁式压电俘能器振动特性研究

2022-01-12张旭辉

振动工程学报 2021年6期

张旭辉，汪林，左萌，佘晓

（1.西安科技大学机械工程学院，陕西西安710054；2.陕西省矿山机电装备智能监测重点实验室，陕西西安710054）

引言

无线传感网络的高速发展使无线传感器在煤矿井下采掘设备的状态监测中得到越来越广泛的应用，但供能问题仍是限制其发展的关键因素［1］。压电振动能量收集技术通过压电效应将环境中的振动能采集并转化成电能而备受关注［2-4］，利用压电自俘能技术有望解决煤矿井下复杂环境中无线监测节点的供电难问题［5-6］。

由于传统线性压电俘能器工作频带窄，俘能效率低，且环境振源具有宽频带、多方向等特点，为此国内外专家学者提出多种压电俘能器以适应环境特点，提升俘能效率。Nguyen等［7］提出一种具有两自由度的双稳态压电俘能器，通过结构参数优化使各个自由度离散的共振频率接近，从而形成共振频率带以拓宽频带。Zhou等［8］提出了一种改进式的三稳态压电俘能器，通过调节底部两个可调磁铁的角度及间距能够有效地拓宽压电俘能器的响应带宽，提高能量收集效率。Liu等［9］提出一种双稳态压电俘能器，并采用谐波平衡法对系统动力学方程求解，探讨了系统阻尼、刚度等参数对俘能器性能的影响。对于环境激励多方向的特点，刘祥建等［10］提出一种蒲公英式新型压电式振动能量收集器，具有多方向振动敏感性。Yang等［11］提出了多束组装的概念，设计了一种新的“MC-PEH”结构，采用弯曲的悬臂梁替代传统直梁，能够有效拓展工作带宽，提高电压输出能力，但并未考虑系统输出功率与外接负载间关系。

针对煤矿井下环境振动多方向、宽频带特点，本文提出一种线形-拱形组合梁式双稳态压电俘能器，通过磁化电流法建立磁场非线性模型，利用广义Hamilton原理建立系统分布式参数模型并进行无量纲化处理，采用谐波平衡法求解系统无量纲化动力学方程，揭示俘能器在不同磁铁间距、激振频率、激励幅值、阻抗等参数下幅频响应及功率输出的规律，最后进行实验测试验证理论结果的正确性。

1 压电俘能器结构及理论模型

线形-拱形组合梁式双稳态压电振动俘能器的结构原理图如图1所示。该结构主要由基座、组合梁、压电薄膜和永磁体构成。其中，为增强系统对现实环境振动源的方向敏感性，悬臂梁采用线形和拱形组合而成。悬臂梁水平距离为L，永磁体A与对面固定端永磁体B磁极相反，磁铁间距为d，调整永磁体间距d可以改变磁铁间排斥力大小。在沿z轴外界振动激励作用下，悬臂梁做上下振动，粘贴在悬臂梁上的压电材料同时产生形变，从而利用压电材料的正压电效应将实际环境中的振动能量转换成电能。

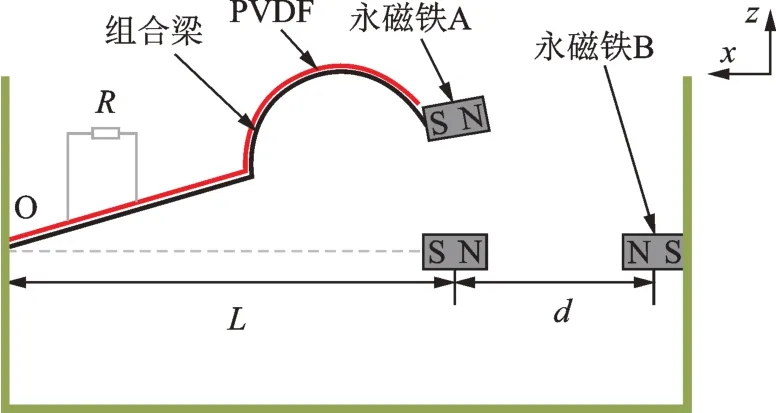
图1 组合梁式双稳态压电俘能器结构原理图Fig.1 Structural schematic diagram of the BPEH based on composed beam

1.1 磁场非线性模型

为构建永磁体A，B间磁场非线性模型，本文采用磁化电流法［12］对两磁铁间非线性磁力进行建模分析，永磁铁间几何关系如图2所示。

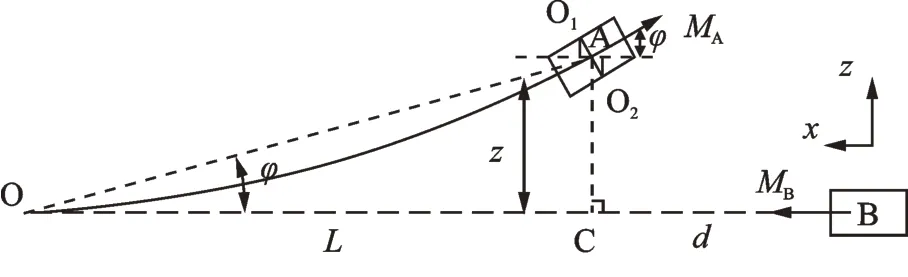
图2 磁铁结构简图Fig.2 Magnet structure diagram

组合梁自由端磁铁磁化强度为mA，固定端磁铁磁化强度为mB，当组合梁处在水平位置时，以固定磁铁B的中心为坐标原点建立坐标系，记磁铁A上下表面中心点分别为O1和O2，磁铁A与水平方向夹角为φ。组合梁长度为L；磁铁A和B的长、宽、高分别为lA，lB，wA，wB，hA，hB；d为组合梁水平时两磁铁间距离。悬臂梁固定端记为点O，磁铁中心A点在水平方向的映射记为点C。由于组合梁刚度很高，故近似认为组合梁为小角度振动，因此可近似得AO=L+lA2，悬臂梁与水平方向的夹角为φ，由几何关系可以得到假设磁铁产生的磁场在空间中分布均匀，依据磁化电流方法，磁铁A与B间产生的磁力大小为

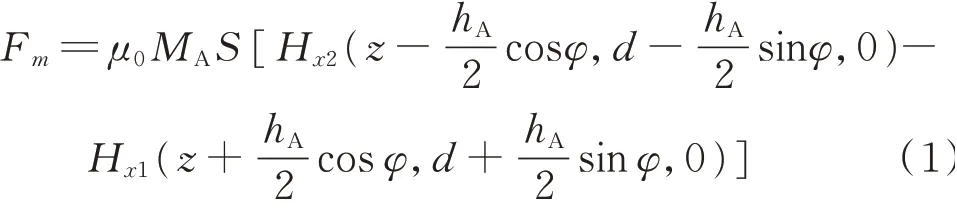
式中MA为磁铁A的磁化强度，S为磁铁A上下面表面积，z为组合梁自由端磁铁A的垂直位移，Hx1和Hx2分别表示磁铁B产生的磁场在磁铁A的上表面和下表面中心处沿x轴方向上的磁场强度大小，其表达式为

通过曲线拟合方式，将磁力表达式简化为关于位移u(L，t)的多项式表达式

图3和4分别为不同磁铁间距下的磁力曲线图及双稳态压电俘能器系统势能曲线图。对比两图可知，当磁铁间距d=10 mm时，磁铁间相互作用力较大，系统势能曲线出现两个对称的势阱，系统呈双稳态特性，此时势阱较深，系统若要产生大幅阱内运动需要消耗大量能量，即需要获得足够大的外部激励，否则系统只能做小幅阱内运动；随着磁铁间距增大（d=15 mm），磁铁间相互作用力整体逐渐减小，磁场势能减弱，双稳态压电俘能器势阱变浅，此时系统仅需较小的外部激励就能产生大幅阱内运动；继续增大磁铁间距（d=20 mm），此时磁铁间磁力及磁场势能进一步减弱，系统双稳态运动特性向单稳态运动特性转化。

图3 变磁距磁力曲线图Fig.3 Magnetic force curve under different magnet distance

1.2 压电俘能器动力学模型

依据广义Hamilton变分原理，压电俘能器系统Lagrange函数的变分在任意时间段t1和t2内等于0，即系统满足

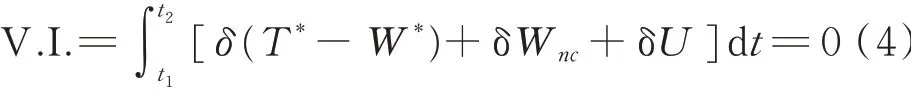
式中T*为系统总动能，W*为系统内部电能，Wnc为系统外力虚功，U为系统总势能，可分别表示为：

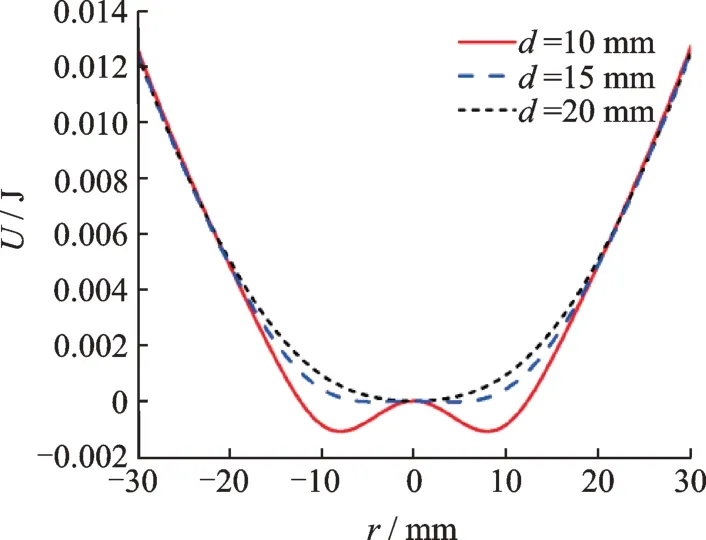
图4 双稳态压电俘能器系统势能曲线图Fig.4 Potential energy curve of bistable piezoelectric energy harvester system

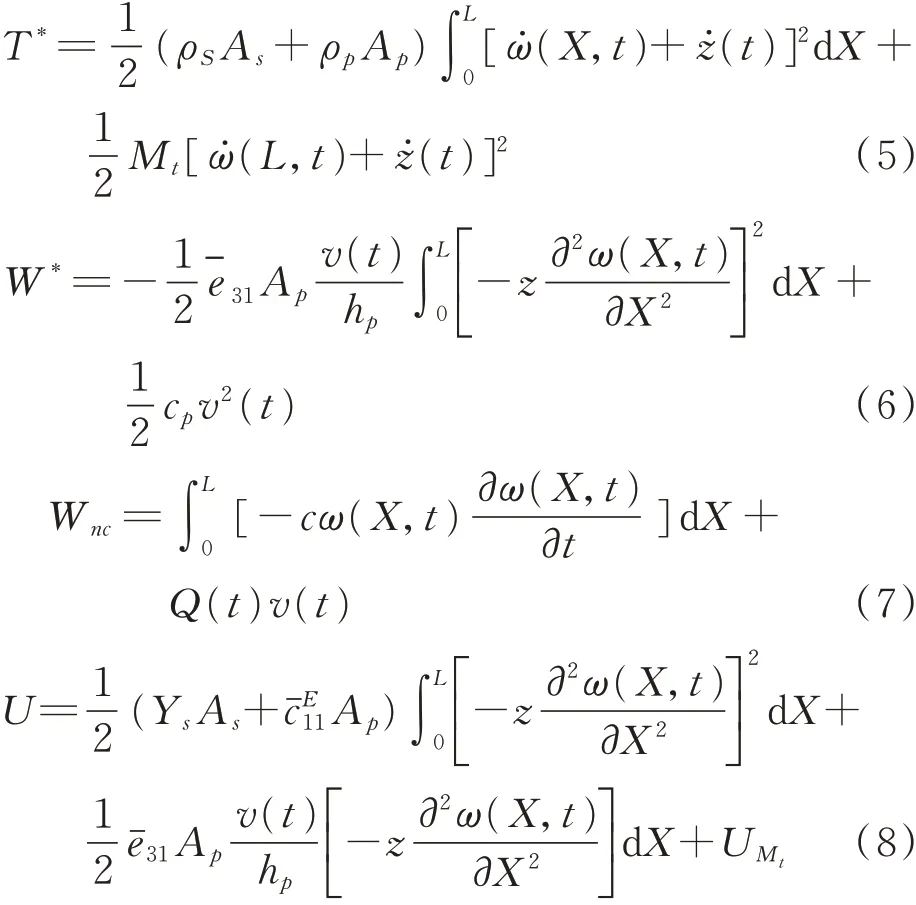
式中ρS为组合梁密度，As为组合梁横截面积，ρp为压电薄膜密度，Ap为压电薄膜横截面积，z(t)为外界基础激励为压电应力常数，hp为压电薄膜厚度，z为组合梁表面到中性层的距离，cp为压电薄膜电容，Q(t)为系统产生电荷量，v(t)为压电薄膜两端电压，Ys为组合梁弹性模量为压电薄膜弹性模量，UMt为磁场势能。

假设ω(X，t)为悬臂梁上某一点在t时刻沿z轴方向的位移，悬臂梁满足Rayleigh-Ritz原理［13］，且低频激励下，组合梁的振动主要集中在一阶模态，忽略二阶及以上的模态函数，悬臂梁一阶振动相对位移ω(X，t)及模态函数Ø1(X)分别表示为

依据压电本构方程、基尔霍夫定律，结合式（4）-（9）得到系统的动力学表达式

式中M，C，K分别表示为系统的模态质量、模态阻尼和模态刚度；ϑ，β分别为机电耦合系数和基础激励系数；r1(t)为悬臂梁振动位移；设z(t)=Asinωt；R为外接负载。

其中：

式中x为无量纲的振动位移；u为无量纲的输出电压；ζ1为无量纲的线性阻尼；κ1为无量纲的线性刚度系数；κ2为无量纲的非线性刚度系数；θ为无量纲的压电耦合系数；e31表示压电应力常数；f为基础激励系数，Ø1(x)为悬臂梁振动容许函数。

2 谐波平衡法求解动力学方程

对于非线性系统响应的近似解析方法较多，其中谐波平衡法是一种较为准确分析非线性系统频响函数的近似解析方法，因此本文采用谐波平衡法对系统动力学方程进行解析，则式（11）的稳定解可以表示为

式中a0表示系统的平衡位置为第i阶模态位移的振幅为无量纲后激励频率。

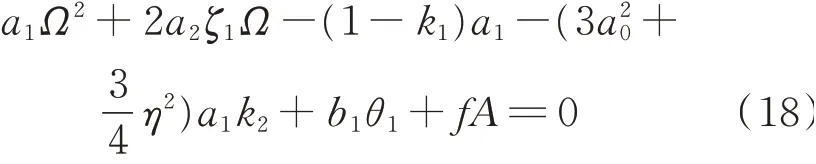
式中A表示外界激励加速度幅值。

根据式（21），（22）可以得到b1和b2的稳态值，即

将b1，b2的值代入式（18）和（19）中，并左右两边平方相加可得

式中a0表示系统的平衡位置，由式（20）可得a0的稳态值a00=0或者将a0的值代入式（24），得到系统稳态振幅η0。

则双稳态压电俘能器输出电压及平均输出功率分别为：

由于采用谐波平衡法求解得到的实数解中可能包括不稳定解，通常非线性系统的多解结果中，最大（高分支）和最小（低分支）解是稳定的，可以通过实验得到验证，而中间解是不稳定的［14］。

3 压电俘能系统仿真结果与分析

3.1 双稳态压电俘能器幅频响应特性

图5所示为不同磁铁间距下，组合梁式双稳态压电俘能系统幅频响应特性曲线，选取激励加速度幅值A=1.3g，磁铁间距分别取d=［14，18，22］mm及无磁力状态。图5（a）为磁铁间距d=14 mm时系统响应频谱，频谱图向右倾斜，系统表现为渐硬特性，系统分别在Ωhigh=1.34和Ωlow=0.93处出现跳跃现象。在Ωlow＜Ω＜Ωhigh处，系统处于不稳定区域，存在多解现象，此时系统包含三个实数解，其中虚线段为不稳定解，实验中无法进行观测。随着磁铁间距的增大（图5（b）和（c）分别对应磁铁间距d=18 mm与d=22 mm），系统不稳定区域逐渐变窄，这说明在一定磁铁间距范围内，非线性磁力对系统的响应频带宽度会产生一定影响，并且随着磁铁距离的增加，频带宽度减小；继续增大磁铁间距，系统最后将处于无磁力状态，如图5（d）所示，且系统响应位移随着磁铁间距的增大略有增加。

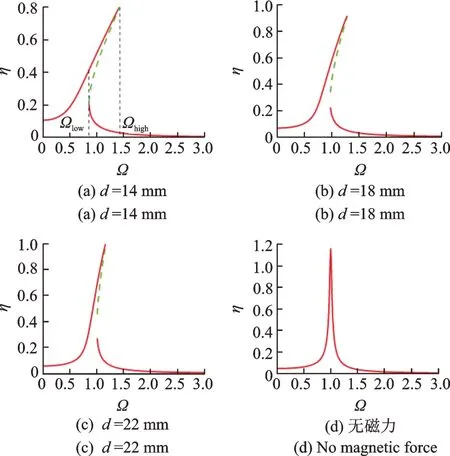
图5 变磁距系统幅频响应曲线Fig.5 Amplitude-frequency response curve of the system under different magnetic distances

图6所示为不同激励加速度幅值A下，组合梁式双稳态压电俘能系统幅频响应特性曲线，选取磁铁间距d=16 mm，激励幅值A=［0.1g，0.5g，1g，1.3g］。图6（a）为激励幅值A=1.3g时系统幅频响应曲线，此时系统不稳定解区域宽度为0.41，随着激励幅值的减小（图6（b）和（c）中激励幅值分别为A=1g和A=0.5g），系统非线性响应减弱，不稳定解区域变窄，且幅值减小，当激励幅值A=0.1g时，如图6（d）所示，此时系统响应幅值缩小5倍，表现为线性系统，这是由于激励不足，难以使系统越过势垒，系统作小幅阱内运动。这说明随着外界激励大小对双稳态压电俘能系统的响应频带宽度及响应幅值均会产生影响。

图6 变激励幅值系统幅频响应曲线Fig.6 Amplitude-frequency response curves of the system under different excitation amplitudes

3.2 双稳态压电俘能器功率输出响应特性

图7给出了系统在大幅阱间运动时（磁铁间距d=16 mm，激励A=1g），俘能器的输出功率随负载阻抗变化的曲线关系，并比较了不同频率（Ω=［0.8，1，1.2］）下的输出功率。由图可知，对于一定的外界激励频率Ω下，俘能器输出功率随着外接负载的增大先增大后减小；当Ω从0.8增加至1.2，俘能器输出功率逐渐增大，这是由于激振频率增大时，系统响应幅值增大，压电薄膜形变变大；且系统最优阻抗值随Ω增大逐渐减小，说明Ω对系统最优阻抗值影响很大。

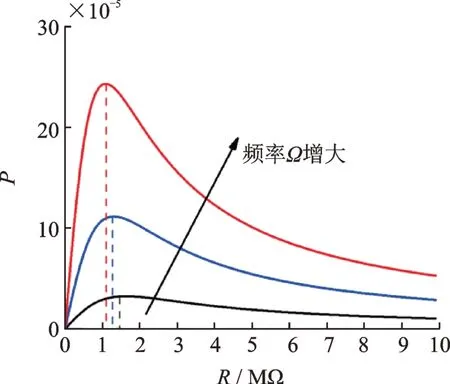
图7 变激励频率俘能器输出功率随负载变化曲线Fig.7 Curve of energy harvester output power with resistance under different excitation frequencies

图8给出了系统在大幅阱间运动时（磁铁间距d=16 mm，Ω=1），俘能器的输出功率随负载阻抗变化的曲线关系，并比较了不同加速度幅值（A=［0.8g，1g，1.3g］）下的输出功率。由图可知，在一定的外接负载R下，俘能器输出功率随外界激励幅值A的增大而增大，但系统最优阻抗值不随激励幅值的增大而改变，维持在1.3 MΩ附近，说明A对系统最优阻抗值影响较小。

图8 变激励幅值俘能器输出功率随负载变化曲线Fig.8 Curve of energy harvester output power with resistance under different excitation amplitudes

图9给出了系统在大幅阱间运动时（Ω=1，A=1g），俘能器的输出功率随负载阻抗变化的曲线关系，并比较了不同磁铁间距（d=［16，18，20］mm）下的输出功率。由图可知，在一定的外接负载R下，俘能器输出功率随磁铁间距d的增大而减小，但最优阻抗值不随磁铁间距的改变而变化，维持在1.3 MΩ附近，说明磁铁间距d对系统最优阻抗值影响较小。

图9 变磁距俘能器输出功率随负载变化曲线Fig.9 Curve of energy harvester output power with resistance under different magnetic distances

4 压电俘能系统实验验证

为验证系统参数对压电俘能器幅频响应及功率输出的正确性，搭建实验测试平台进行实验验证，如图10所示。通过调节压电俘能器实验样机（如图11所示）上的可调夹具来调节两磁铁间距离，进而调节磁力的大小。实验中，将双稳态压电俘能器样机放置在激振台上，振动控制台产生正弦信号通过功率放大器放大后作用于激振台并带动俘能器振动，通过示波器实时测得俘能器振动时输出电压。

图10 俘能器性能测试实验平台Fig.10 Energy harvester performance testing experimental platform

图11 俘能器结构图Fig.11 Structural diagram of the BPEH

煤矿井下采煤机摇臂电机轴主要振动频率范围在10-30 Hz之间［15］，为了更好地得出在不同负载阻抗条件下压电俘能器的输出响应，实验时通过扫频与定频相结合的方式。图12为激励加速度幅值A=1.3g，磁铁间距分别取d=［14，18，22］mm及无磁力状态下俘能器电压输出图。可以看出实验测得的俘能器输出电压随频率的变化规律与仿真结果中系统幅频响应特性曲线一致，当磁铁间距d=14 mm时（图12（a）所示），系统大幅响应频带较宽，随着磁铁间距增大，系统大幅响应输出带宽随之减小，最大输出电压略有增大，最大可达52.6 V，且系统共振点右移。当磁铁间距增加至22 mm时（图12（c）所示），系统几乎处于无磁力状态，大幅响应带宽骤减，响应输出与无磁铁时类似（图12（d）所示）；系统输出正负电压峰值出现不对称现象，这是由于组合梁中拱形梁部分在变形过程中存在横向与纵向形变，使得压电薄膜的形变非对称而产生电压幅值不对称。

图12 变磁距俘能器输出电压扫频图Fig.12 Sweep diagram of energy harvester output voltage under different magnet spacings

图13为磁铁间距d=16 mm，A=1g时俘能器电压输出正向、反向扫频图。当俘能器做正向扫频实验，f＜18.6 Hz时，系统电压输出响应稳定，且峰值随频率增大缓慢递增；当频率增加至18.6 Hz时，系统稳态响应出现跳跃现象，响应输出急剧下降，随后随频率增加缓慢下降；当俘能器做反向扫频实验，f＞15.3 Hz时，电压响应输出稳定，且峰值随频率减小缓慢递增，随着扫频频率减小至15.3 Hz，俘能器输出响应出现跳跃现象，响应输出呈脉冲式升高，随后随扫频频率减小缓慢下降，与仿真结果规律保持一致。

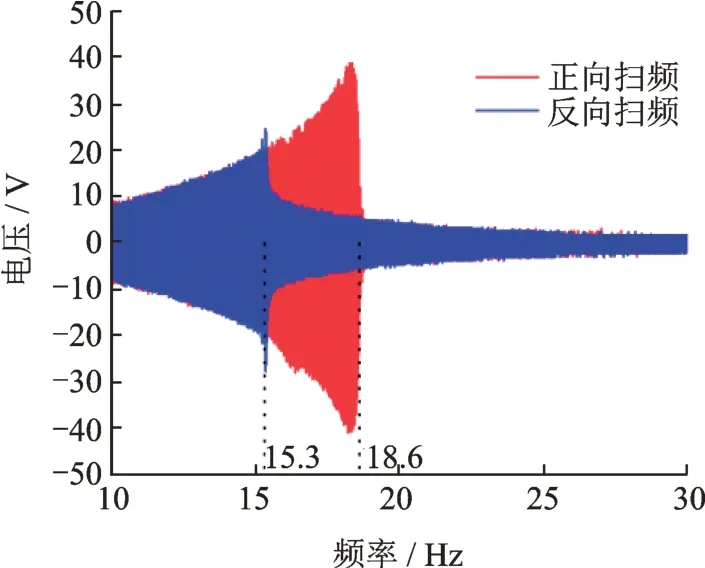
图13 俘能器输出电压扫频图Fig.13 Sweep diagram of energy harvester output voltage

图14为磁铁间距d=16 mm，激励加速度幅值分别取A=［0.5g，1g，1.3g］时俘能器电压输出响应图。可以看出实验结果与仿真结果规律一致，当激励幅值A=0.5g时，外部激励较小，系统无足够大能量做大幅阱间运动，此时系统做小幅阱内运动，输出电压较低，随着外部激励增大（A=1g），系统做大幅阱间运动，输出电压变大，大幅响应频带变宽，继续增加激励（A=1.3g），此时系统响应带宽及响应幅值略微增大，幅度较小，系统已达到饱和状态。

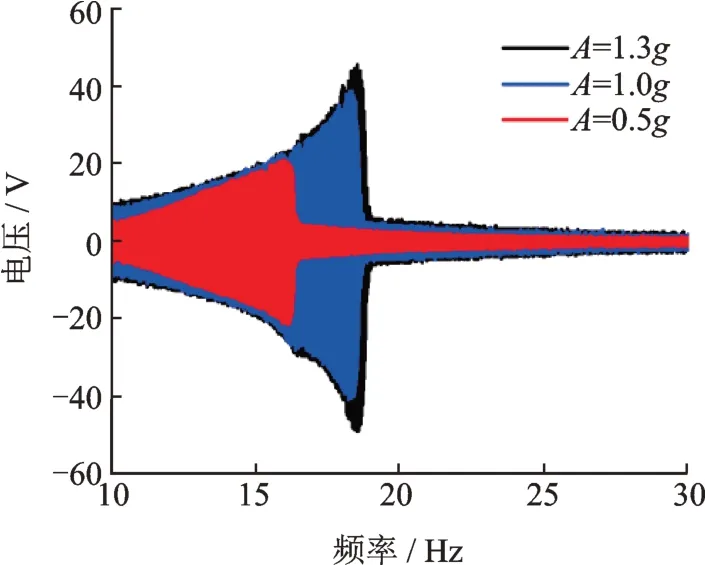
图14 变激励幅值俘能器输出电压扫频图Fig.14 Sweep diagram of energy harvester output voltage under different excitation amplitudes

图15 为磁铁间距d=16 mm，激励加速度幅值A=1.3g，激振频率f=［15.8，16，16.2］Hz时，俘能器输出功率随外接电阻变化规律图。由图可知，f=15.8 Hz时，俘能器输出功率随着外接电阻阻值增大先增后减，最优阻抗值R=5.8 MΩ，此时最大输出功率约为28.69 μW。随着激振频率的增大（f分别取16，16.2 Hz），俘能器输出功率逐渐增大，最大值约为43.4 μW，且系统最优阻抗值随激振频率增大逐渐减小（f=16 Hz时，最优阻抗为5.6 MΩ；f=16.2 Hz时，最优阻抗为5.32 MΩ），与仿真结果规律保持一致。

图15 变激振频率俘能器输出功率响应曲线Fig.15 Energy harvester output power response curve under different excitation frequencies

图16为磁铁间距d=16 mm，激振频率f=16 Hz，激励加速度幅值A=［1g，1.2g，1.3g］时，俘能器输出功率随外接电阻变化规律图。由图可知，激励加速度幅值A=1g时，俘能器输出功率随着外接电阻阻值增大先增后减，最大值约为30.2 μW，随着加速度幅值增大（A分别取值1.2g，1.3g），俘能器输出功率逐渐增大，最大值约为35 μW，且系统最优阻抗值不随激励幅值的改变发生明显变化，维持在5.6 MΩ，与仿真结果规律一致。

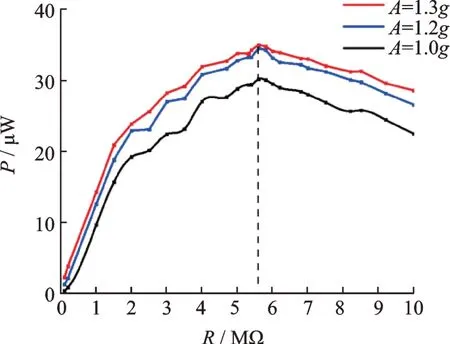
图16 变激励幅值俘能器输出功率响应曲线Fig.16 Energy harvester output power response curve under different excitation amplitudes

图17为激振频率f=16 Hz，激励加速度幅值A=1.3g，磁铁间距d=［16，18，20］mm时，俘能器输出功率随外接电阻变化规律图。由图可知，磁铁间距d=20 mm时，俘能器输出功率随着外接电阻阻值增大先增后减，最大值约为30.6 μW，随着磁铁间距减小（d分别取18，20 mm），俘能器输出功率逐渐增大，最大值约为35 μW，且系统最优阻抗值不随磁铁间距的改变发生明显变化，与仿真结果规律一致。