基础振动作用下转子-轴承-密封系统动力学分析

2022-01-12张恩杰焦映厚陈照波武祥林王治易

振动工程学报 2021年6期

张恩杰，焦映厚，陈照波，武祥林，张赛，王治易

（1.上海宇航系统工程研究所，上海201109；2.哈尔滨工业大学机电工程学院，黑龙江哈尔滨150001）

引言

船舶汽轮机安装在易变形的船体基座上，受风浪或爆炸冲击等作用的影响，基础振动易由轴承传递至轴径，给转子系统的安全稳定运行带来隐患。而狭窄间隙中的高温高压流体，作为汽轮机转子系统的主要激励源，对转子系统的非线性动力学特性影响显著。多年来，科研人员对基础振动或密封流体激振的转子系统开展了大量研究。Duchemin等［1］、Driot等［2］分析了基础振动频率对简支转子系统的稳定性和动态特性的影响规律。Ying等［3］建立了涡轮增压器转子系统的集总参数模型，分析了经由轴承油膜传递至转子的发动机激励对系统非线性动力学特性的影响。EI-Saeidy等［4］分析了线弹性轴承和非线性轴承支承的转子系统在基础振动影响下的频响特性，研究指出应以轴径而非轮盘的响应幅值作为系统振动的评价参数。Dakel等［5］基于Timoshenko梁理论建立了基础运动的转子系统的动力学模型，采用解析法和数值法分析了转轴/轮盘的结构不对称和基础的转动对系统稳定性的影响。Zhang等［6］分析了基础俯仰和滚转运动时的转子-轴承系统的非线性动力学特性及稳定性，Han等［7］研究了基础时变振动影响下的裂纹转子-轴承系统的动态响应。此外，一些学者还对受地震激励、随机冲击载荷作用的转子系统的动力学响应开展了相关研究［8-11］。在密封流体激振影响方面，科研人员也进行了深入研究。其中，Muszynska所提出的非线性密封力模型［12-13］被广泛应用于转子-密封系统的动力学特性分析和稳定性分析［14-18］中。Wang等［19-20］和Zhang等［21］则基于摄动法、控制体理论及Muszynska模型提出了更适用于迷宫密封的流体激振力模型，并对转子-轴承-密封系统进行了动力学特性分析及稳定性评估。

目前在对基础振动的转子系统进行动力学或振动特性分析时，并未考虑密封流体激励的影响。已有研究虽能为转子系统的动力学设计、振动分析或故障诊断提供参考，但是对于多激励因素共同作用的船舶汽轮机转子系统，只有在建立其动力学模型时尽可能全面地将各关键影响因素考虑在内，才能给出更为准确可靠的结果。鉴于此，本文以船舶汽轮机为应用对象，计入密封流体、轴承油膜及不平衡量的影响，建立基础振动的转子系统的动力学模型，分析基础振动对系统非线性动力学特性的影响。

1 基础振动的转子系统动力学模型

对于基础振动的转子系统（如图1所示），为方便其动力学模型的构建及动态特性的分析，引入以下两个坐标系：1）全局坐标系Fg，其原点为Og；2）固定于转子系统基础上的运动坐标系Fb，其原点为Ob。则坐标系Fb与Fg之间存在以下关系

图1 基础振动的转子系统Fig.1 Rotor system excited by base vibration

式中正交矩阵Tbg=Rβ Rα Rγ；γ，α和β为惯性坐标系Fg转换到与非惯性坐标系Fb相平行的位置所依次转过的欧拉角（如图2所示），这三者可分别用于表示基础的滚转、俯仰和偏航运动的角位移；Rα，Rβ和Rγ分别为α，β和γ的函数关系的矩阵表示。

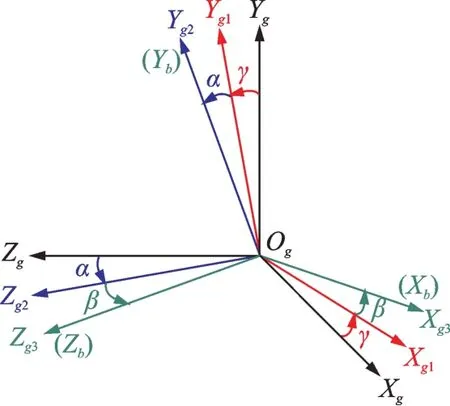
图2 坐标系的转换Fig.2 Transformation of coordinate systems

则在全局坐标系Fg中，轮盘中心的绝对速度可表示为

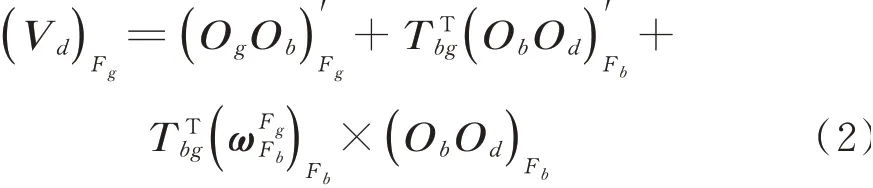
式中(OgOb)Fg为向量OgOb在Fg中的表示；(ObOd)Fb=(Ob A)Fb+{Xd Yd ld}T，(Ob A)Fb为左轴承中心A在Fb中的位置向量，Xd，Yd和ld分别为轮盘中心沿Xb和Yb轴的位移及其到左轴承中心的距离为Fb相对于Fg的转速，表示如下

轮盘的偏心集中质量位于点nub处，其绝对速度的表达式为

式中rub和ηub分别为不平衡质量mub的偏心距和偏心角；ω为转子转速。

受基础振动作用的转子系统的动能、势能及耗散势能的表达式如下

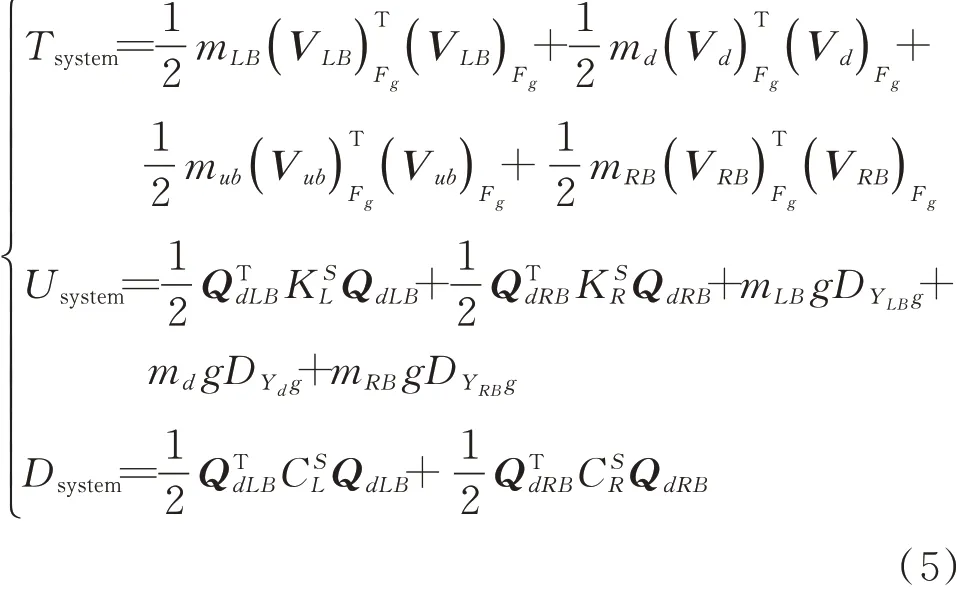
式中mLB，mRB和md分别为左、右轴径和轮盘的集中质量；(VLB)Fg和(VRB)Fg分别为左、右轴径的绝对速度，表达式与（2）相似；QdLB和QdRB分别为左右轴径的状态向量，KSL和CSL分别为左轴段的刚度和阻尼；KSR和CSR分别为右轴段的刚度和阻尼；DYLB g，DYRB g和DYd g分别为左、右轴径和轮盘在Fg中的绝对竖坐标。

依据Lagrange方法，结合以上各式，可得基础振动的转子-轴承-密封系统的动力学方程为

式中msy和Qsy分别为系统的质量矩阵和状态向量；Csy1和Csy2为系统的阻尼矩阵；Ksy1和Ksy2为系统的刚度矩阵；cf1，cf2和cf3分别为由基础的转动、平动及二者的耦合作用引起的系数矩阵；cf4为与基础转动有关的重力系数矩阵；cf5为由基础和转子转动引起的不平衡系数矩阵；Fw为作用于转子的外力矩阵，表示如下

式中FLB□，FRB□和Fd□分别为作用于左、右轴径的非线性油膜力和作用于密封轮盘的非线性流体激振力［21］。

为便于计算分析，对式（6）进行无量纲化处理，可得

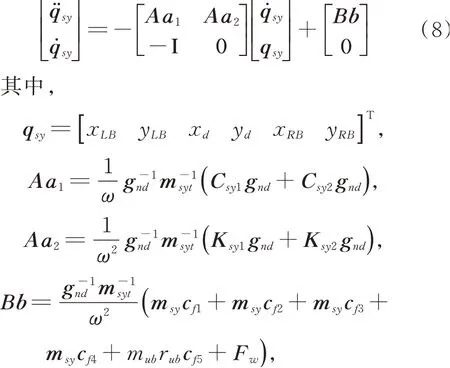
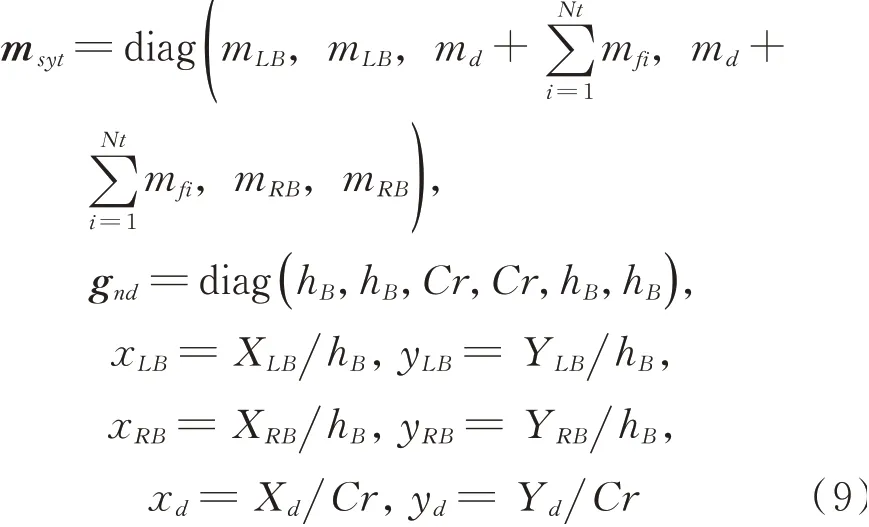
式中hB和Cr分别为滑动轴承间隙和迷宫密封间隙；Nt为密封齿数。

2 基础振动的转子系统动力学特性分析

2.1 基础振动对转子系统动力学特性的影响

采用Newton-Raphson法求得密封齿腔内介质压力与泄漏量，应用Gauss-Jordan法及数值积分获取齿腔内密封力，并结合Muszynska模型得到迷宫密封整体的非线性流体作用力［21］，同时根据Capone模型计算滑动轴承油膜力［22］，进而采用Runge-Kutta法求解转子系统动力学方程，对比分析基础振动对系统动态特性的影响。转子、轴承及迷宫密封的结构参数如表1所示。

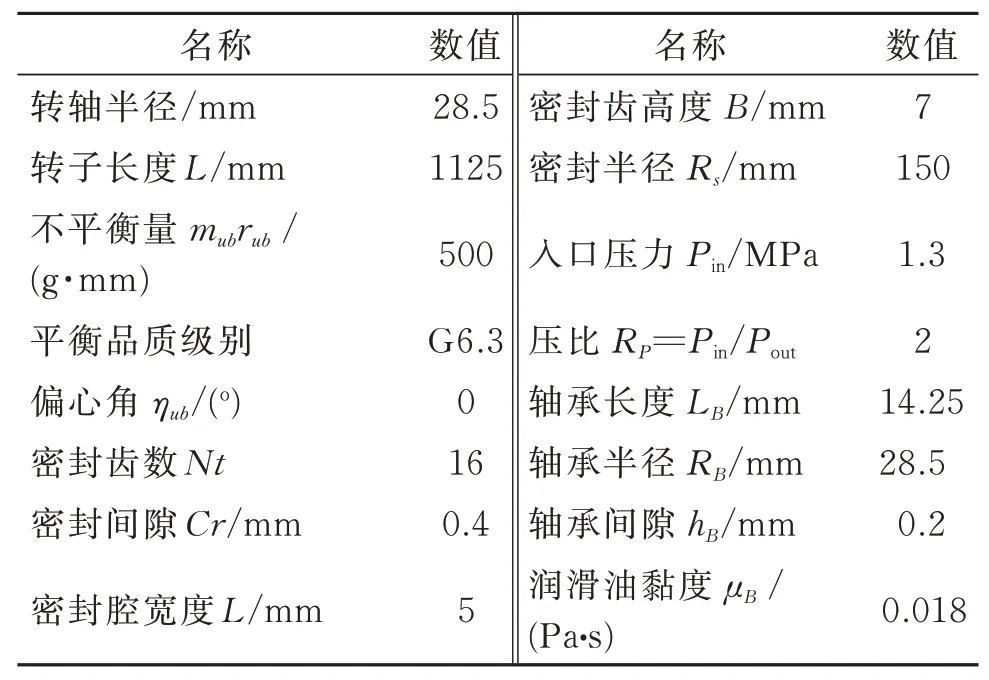
表1 转子-轴承-迷宫密封系统的结构参数Tab.1 Structure parameters of rotor-bearing-labyrinth seal system

基础无振动时，在不平衡量、轴承油膜和密封流体的激励作用下，置于转子跨中的密封轮盘的振动频谱及运动分岔特征如图3所示。转速ω在500-9250 r/min的范围内，系统振动主要由转子不平衡诱发，瀑布图中以工频fr为主，其他频率特征不明显；分岔图中每一转速下的Poincaré映射点重合，显示为仅有一个点；频谱及分岔特征表明，转子系统在该转速范围内以单周期形式运动。ω由9250 r/min增大至12750 r/min时，流体激振频率fwl随之由69.4 Hz增大至96.7 Hz，fwl≈0.45fr；在此转速域内，滑动轴承和迷宫密封的狭窄间隙内的流体激振作用增强，系统动态响应的非线性特征显著，分岔图中每一转速下都存在多个互不重合的映射点，系统表现为概周期运动。随着转速的继续增加（12750 r/min＜ω＜15000 r/min），工频fr的幅值依然很小，幅值最大的自激振动频率fwp在[96.7，97.5]Hz的范围内做微小变化，该锁频现象归类为流体振荡［23］。

图3 无基础振动时转子-轴承-密封系统的动力学响应Fig.3 Dynamic responses of rotor-bearing-seal system without base excitation

为更直观地了解系统的振动情况，以振动烈度来表征转子的振动。振动烈度的定义为

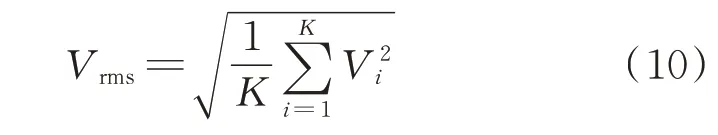
式中Vi(i=0，1，⋅⋅⋅，K-1)为振动速度离散信号。由图4可知，流体涡动发生之前（ω＜9250 r/min），不平衡量、轴承油膜和密封介质的激励作用使得振动能量在轴径和轮盘处非同步地积累和耗散，右轴径和密封轮盘的横向振动烈度在2750，4000和8500 r/min时交替出现极大值，但其值均小于18 mm/s。出现流体涡动时，系统振动极速增强，轴径及轮盘在各自的X和Y方向上的振动烈度基本相等，密封轮盘的振动比轴径更为剧烈。流体振荡发生后，系统的振动烈度维持在很高的水平，随转速变化的幅度较小。需要指出的是，左右轴径的频谱特征、分岔特性及振动情况均一致。

图4 无基础振动时转子-轴承-密封系统的振动烈度Fig.4 Vibration intensity of rotor-bearing-seal system without base excitation

受到基础俯仰振动（α=α0cosωbt，α0=0.1°，ωb=20 Hz）作用时，转子系统的动力学响应如图5所示。转速很小时，系统即发生失稳，频谱图中基础振动频率fwb及其N倍频（Nfwb）的幅值均大于工频幅值，分岔图中每一转速下均有多个映射点，系统呈概周期运动。基础的俯仰振动向系统持续输入能量，对比图6和图4可知，其使得同一转子系统的横向振动烈度增大，系统振动显著增强。随着转速的增加，系统在X方向上的振动烈度逐渐增大，Y方向上的则一直保持在较大的水平，均大于23 mm/s，且转轴上密封轮盘Y方向的振动最为剧烈。由于基础振动的存在，系统发生流体涡动的转速门槛值由9250 r/min降低至8250 r/min。涡动频率fwl出现时，基础振动频率及其N倍频分量的幅值快速减小或消失，fwl成为主振动频率；与无基础振动时相似，系统的振动烈度快速增大；这表明流体自激振动的影响逐渐大于基础振动作用，成为主激振因素。流体涡动发生后，系统的Vrms-ω变化趋势与无基础振动时的一致。对比图5（a）和图3（a）可知，不考虑基础振动时，系统发生流体振荡的转速门槛值为12750 r/min，此时流体振荡频率与工频之比（fwp fr）为0.455。fwp fr与流体平均环流比正相关，流体平均环流比与失稳转速负相关。由于流体平均环流比的增加，考虑基础振动后，系统失稳转速降低，发生流体振荡的转速门槛值减小至12000 r/min（fwp fr=0.49）。

图5 基础振动时转子-轴承-密封系统的动力学响应Fig.5 Dynamic responses of rotor-bearing-seal system subjected to base excitation

图6 基础振动时转子-轴承-密封系统的振动烈度Fig.6 Vibration intensity of rotor-bearing-seal system subjected to base excitation

2.2 基础振动频率对转子系统动力学特性的影响

将基础俯仰振动幅值α0及转子转速ω分别保持在0.1°和4000 r/min，仅改变俯仰振动频率ωb，计算得到转子系统的动力学响应如图7所示。当ωb≤12 Hz时，fwb（=ωb）的幅值略小于工频幅值，轴径及轮盘的各向振动烈度均较小（≤7.1 mm/s），系统运转平稳。随着ωb的增加，主振动频率fwb（=ωb）的幅值整体呈线性增大趋势，其N倍频（2fwb，3fwb，4fwb）的幅值大于工频幅值；轮盘在不平衡量及密封流体的激励下，对基础俯仰振动最敏感，其Y向振动最剧烈，振动烈度由ωb=12 Hz时的7.1 mm/s快速增大至ωb=100 Hz时的245.7 mm/s，振动情况严重恶化。轴径的Y向振动烈度次之，其在接近ωb=28 Hz的过程中增速减缓，后随ωb的增加快速增大。ωb≥28 Hz时，轮盘X向的Vrms先增大后减小，并于ωb≥76 Hz时逐渐趋于定值。由图8（a）可以发现，在基础俯仰振动频率ωb增加的过程中，轮盘轴心轨迹由椭圆形历经“8”字形逐渐演变为长边在Y向排列、短边为U形的环形。对比图8（a）和图8（b）可知，受基础偏航振动（β=β0cosωbt，β0=0.1°，ω=4000 r/min）影响时，轮盘轴心轨迹恰似将基础俯仰振动时的轮盘轴心轨迹翻转了90°。特别需要指出的是，基础偏航振动时，系统在X和Y向的动力学特性、振动烈度变化特征分别与受俯仰振动影响时转子在Y和X向的动力学特性、振动烈度变化特征相似，因篇幅限制，此处不再展示。

图7 基础俯仰振动频率变化时转子系统的动力学响应Fig.7 Dynamic responses of the rotor system for pitching base excitation with variable base frequency

图8 基础俯仰振动和偏航振动时的转子轴心轨迹Fig.8 Trajectories of rotor system subjected to pitching excitation and yawing excitation of base

将基础滚转振动幅值γ0和转子转速ω分别保持在0.1°和4000 r/min不变，仅改变滚转振动频率ωb，求解可得转子系统的动态响应如图9所示。滚转振动频率较小（ωb≤18 Hz）时，系统的振动烈度小于8.7 mm/s，转子振动幅值很小（图9（b））。由于基础滚转振动对系统X和Y方向的激励作用基本相同，随着ωb的增加，系统各向的振动烈度均增大，转子轴心轨迹也由关于Y轴对称的近似“V”形或三角形逐渐演变为较为规则的四边形。由以上可知，基础旋转振动对转子系统动力学响应的影响具有明确的方向性，基础俯仰和偏航振动的影响分别体现在Y和X方向，滚转振动对X和Y方向上的影响则基本相同。

图9 基础滚转振动频率变化时转子系统的动力学响应Fig.9 Dynamic responses of rotor system for rolling base excitation with variable base frequency

分别将基础竖直方向振动幅值Yb0和转子转速ω保持在10 μm和4000 r/min不变，随基础振动频率ωv变化的系统动力学响应的频谱特性及振动特征如图10所示。转子工频幅值全程保持在较大的水平，频率分量fωv（=ωv）则随ωv的增加先增大，并于ωv=60 Hz时达到最大值后逐渐减小。此外，频谱图中还存在工频与基础振动频率的组合频率分量|fr-fωv|，fr+fωv，|2fr-fωv|。该激励条件下，由于基础振动主要作用在转子竖直方向上，转子Y方向的振动烈度大于其X方向的。ωv较小时，转子X和Y方向的振动烈度分别保持在3.15 mm/s和8 mm/s左右；随着ωv的增加，转子水平方向的在ωv=40 Hz和103 Hz时分别出现最大值和极大值，竖直方向上则于ωv=60 Hz和130 Hz时出现最大值和极大值。

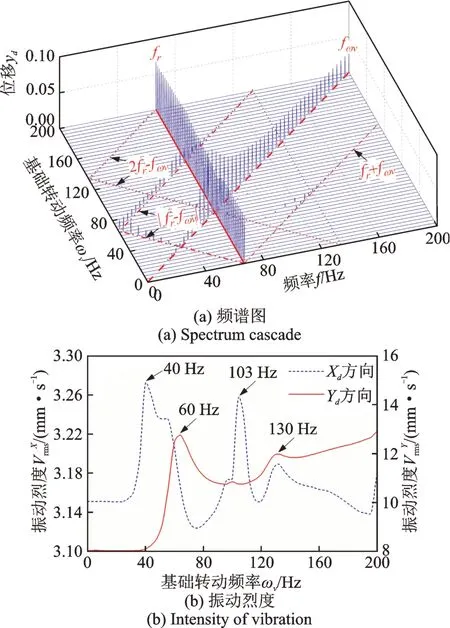
图10 基础竖直方向振动频率变化时转子系统的动力学响应Fig.10 Dynamic responses of rotor system for vertical base excitation with variable base frequency

2.3 基础振动幅值对转子系统动力学特性的影响

对同一转子系统，将基础俯仰振动频率ωb固定在10 Hz，分别在转子转速ω=4000 r/min和6000 r/min的条件下，分析基础俯仰振动幅值α0对系统动力学特性的影响。如图11所示，系统竖直方向的振动最为剧烈；随着α0由0°增大至30°，转速ω=4000 r/min时转子Y方向的振动烈度由8.03 mm/s快速增大至68.99 mm/s，ω=6000 r/min时曲线的变化趋势与之高度相似；α0取值相同的条件下，转速变化对竖直方向振动强度的影响很小。水平方向上，在转速ω=4000 r/min的条件下，振动烈度先由α0=0°时的3.02 mm/s快速增至α0=6°时的14.21 mm/s，之后随着α0的增加缓慢减小至α0=30°时的10.83 mm/s。在ω=6000 r/min时曲线的变化趋势虽与ω=4000 r/min时的相似在α0较小时的增长率却更大，在α0=3°时增至最大值；另外，α0相同取值条件下，水平方向的振动随转速的增加也有所增强。

图11 基础俯仰振动幅值变化时转子系统的振动烈度Fig.11 Intensity of vibration of the rotor system for pitching base excitation with variable amplitude of base excitation

由2.2节可知，基础角振动对转子系统动力学响应的影响具有明确的方向性。对比图12和11可知，基础偏航振动条件下，外源激励作用于X方向，转子系统在水平和竖直方向的振动烈度变化趋势分别与基础俯仰振动时转子系统在竖直和水平方向上的一致；此外，在角振动幅值和转速分别取值相等的情况下，受转子自重影响，基础偏航振动的转子系统的小于基础俯仰振动的转子系统的基础偏航振动的转子系统的则大于基础俯仰振动的转子系统的

图12 基础偏航振动幅值变化时转子系统的振动烈度Fig.12 Intensity of vibration of the rotor system for yawing base excitation with variable amplitude of base excitation

由以上可知，系统受到基础某横向方向上角振动影响时，该方向的振动烈度随角振动幅值的增加而增大，在相同角振动幅值条件下，转速的增加对该向振动烈度的影响较小；但在与之垂直的另一横向方向上，振动烈度随角振动幅值的增加先增大后减小，转速的增加使得该向振动烈度增大。产生以上现象的根本原因，是由于系统动力学方程（6）的系数矩阵中出现了耦合项。

在频率较低（ωb=10 Hz）的基础滚转振动作用下，转子系统水平方向上的振动强于竖直方向（图13和图9（a））。随着滚转振动幅值γ0的增加，系统在水平方向的振动烈度VXrms先增大后减小；竖直方向上，γ0较小时VYrms的增速较快，其在γ0=7°-8°时达到最大值，随后VYrms逐渐减小，并在γ0=18°-20°时减至极小值，之后随γ0的增大略有增加。γ0取值相同时，转速的增加对水平方向振动烈度的影响较小，竖直方向上系统的振动则有所增强。