具有多共存吸引子的忆阻混沌系统分析与同步
2022-01-12王徐盱张宏昊赖强
王徐盱,张宏昊,赖强
(华东交通大学 电气与自动化工程学院,江西 南昌 330013)
忆阻器是用来描述磁通和电荷之间的关系,除电容、电阻、电感之外的第四个基本电路元件。2008年,惠普公司[1]在《自然》 上报道研制出了具有典型忆阻特征的忆阻器,这一结果不仅证明了Chua[2]于1971 年从理论上预测忆阻器存在的准确性,还为电路设计与应用提供了全新的思路和发展空间。忆阻器是一个体积小、能耗低且具有记忆功能的非线性电路元件,因此被广泛应用于构造混沌电路。Lozi 等[3]在蔡氏电路中观察到三种不同的吸引子共存现象。Itoh等[4]采用分段线性模型忆阻器替换经典蔡氏电路中的蔡氏二极管实现了第一个忆阻器混沌系统,而Muthuswamy[5]采用光滑模型忆阻器也完成了类似工作。Bao 等[6]通过分析一个变形蔡氏电路,研究其隐藏吸引子和共存吸引子,并且这些吸引子的吸引域不包括平衡点邻域,因此一般的数值分析方法不适用于探究隐藏吸引子。此外,该学者带领团队又在Chen 混沌系统的基础上构造了一个具有双忆阻器的混沌系统电路,并研究了忆阻系统的隐藏极端多稳态和超混沌[7]。Jin 等[8]提出了两种基于忆阻器的极端多稳态混沌 Shinriki 振荡器,并研究了其 FPGA (Field Programmable Gate Array,现场可编程逻辑门阵列)实现。Li 等[9]将忆阻器与文氏振荡电路结合设计了一类文氏忆阻混沌电路。Wang 等[10]提出一种可产生2N涡卷和2N+1 涡卷混沌吸引子的多分段线性忆阻模型电路,同时该电路还可产生多涡卷共存吸引子。Lai等[11]研究了具有无穷多个共存吸引子的忆阻混沌系统的复杂动力学、电路实现和同步。忆阻器特殊的非线性特性和记忆功能使其具有巨大的潜在应用价值,忆阻混沌系统仍然是近年来学术界和工程界研究的热点。
依赖于初始状态的多稳定性,即多共存吸引子是指一个固定参数集合内的多个吸引子(或平衡态)共存。多共存吸引子的存在表明了系统在固定参数下最终状态的非唯一性。当非线性系统依赖于它的初始值时,运动轨迹会有选择地收敛到不同的稳定状态[12],这种特殊现象主要与有无共存吸引子[7]、几个共存吸引子[13]、甚至无穷多个共存吸引子[14]有关,特别是当共存吸引子的数量趋于无穷多时,这种现象又称为极端多稳定性[15]。在适当的控制下,系统可以实现不同状态之间的转换,以适应多种工作场景。为了进一步探究其多样性和复杂性,研究忆阻混沌系统中共存吸引子是近年来混沌研究的热点。Lorenz 型系统中的蝴蝶型吸引子很容易被分解成两个孤立的对称奇异吸引子[16-17],在一些简单的混沌运动中于不同的初始条件下也观察到并发混沌和极限环[18-19]。Bao 等[20]用简化蔡氏二极管实现了改进蔡氏电路中共存的螺旋型混沌吸引子,并进一步指出由于忆阻器的特殊非线性,忆阻器混沌电路容易产生共存吸引子[7,21]。Lai 等[22]通过多项式函数方法研究了在混沌系统中产生两共存吸引子、三共存吸引子和四共存吸引子。Hens 等[23]根据部分同步的概念提出了一种更新奇的方法来构造耦合动力系统中任意数量共存的混沌吸引子。此外,还有学者建立了一些新的具有不同类型共存吸引子的自治多项式混沌系统[24-25]。因此,寻找一种具有多共存吸引子的忆阻混沌电路是非常有意义的。
混沌同步是混沌研究的另一个重要课题,它是对应于两个或多个混沌系统在不同初始状态下通过内部耦合或外部输入控制最终达到状态一致的过程。混沌同步原理于1990 年由美国学者Pecora 和Carroll[26]提出,他们首次在电子线路上实现了混沌同步。混沌同步按对象性质可分为一般时间混沌系统同步、时空混沌系统同步、超混沌系统同步以及网络的混沌同步等。2000 年Brown 和Kocarcv[27]给出了混沌同步的统一数学定义,按理论研究和实际实验可分为完全同步、广义同步、滞后同步、相同步和Q-S 同步五种同步类型。混沌同步的理论在近些年的研究中,借助于混沌稳定性控制和其他非线性系统的控制方法,提出了多种同步方案,主要有主动-被动同步[28]、反馈同步(线性反馈、非线性反馈)[29]、状态观测器控制[30]、自适应控制[31]、事件触发控制[32]、脉冲控制[33]等,并建立了相应的混沌同步稳定性分析理论。混沌同步的发展大大推进了混沌同步的应用进程,诸如在电子学、化学、生物、脑科学、神经网络系统、密码学以及保密通信等领域中,混沌同步都具有不可估量的应用潜力。
本文以经典混沌理论为基础,构造了一个新的具有多共存吸引子的忆阻混沌系统。对其进行基本动力学特性分析,设计模拟电路进行仿真验证,同时还探究了该忆阻混沌系统的同步控制问题。
1 基于忆阻器的混沌系统
文献[4]提出了忆阻器的定义式为:

式中:v和i分别是流经忆阻器的电压和电流;W(φ)是通过忆阻器的磁通量为忆导函数,定义为:
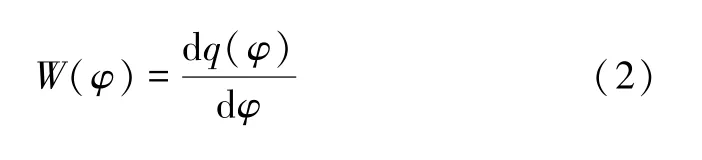
现考虑如下忆导函数[5]:
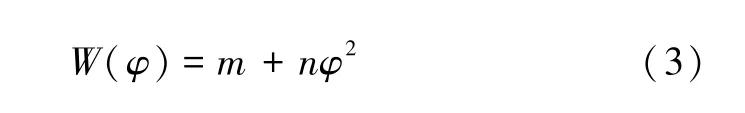
式中:m和n均为常数。
2004 年,Liu 等[34]建立了如下系统:

它能产生一个蝴蝶奇异吸引子,其中参数为a=10,b=40,c=2.5,d=4。就像Lorenz 系统[35],Chen 系统[36]和Lv 系统[37]一样,系统(4)也是具有两个二次非线性项的三维自治系统,通过与电阻或电容相连的乘法器和运算放大器构成的电子电路很容易实现,用忆阻器代替自变量电阻或线性耦合电阻,便可构建出新型忆阻混沌系统。因此,新构造的忆阻混沌系统的无量纲状态方程可表示为:
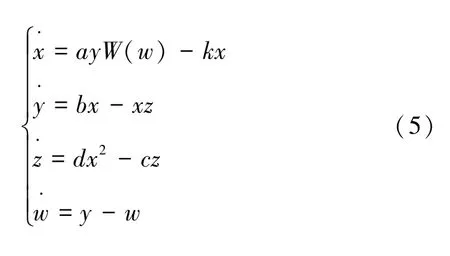
式中:W(w)=m+nw2;a表示忆阻器强度的正参数。仅用W替换系统(4)中的耦合电阻得到新实现的系统不能产生混沌,而用W替换自变电阻所构造的忆阻混沌系统就可以产生混沌,其耗散性也可与系统(4)保持不变。因此,所提的系统(5)是由系统(4)衍生而来的最合适的忆阻混沌系统。
忆阻混沌系统(5)是一个四维光滑非线性动力系统。基于系统(5),通过数值模拟可以观察和分析一些有趣的动力学行为。
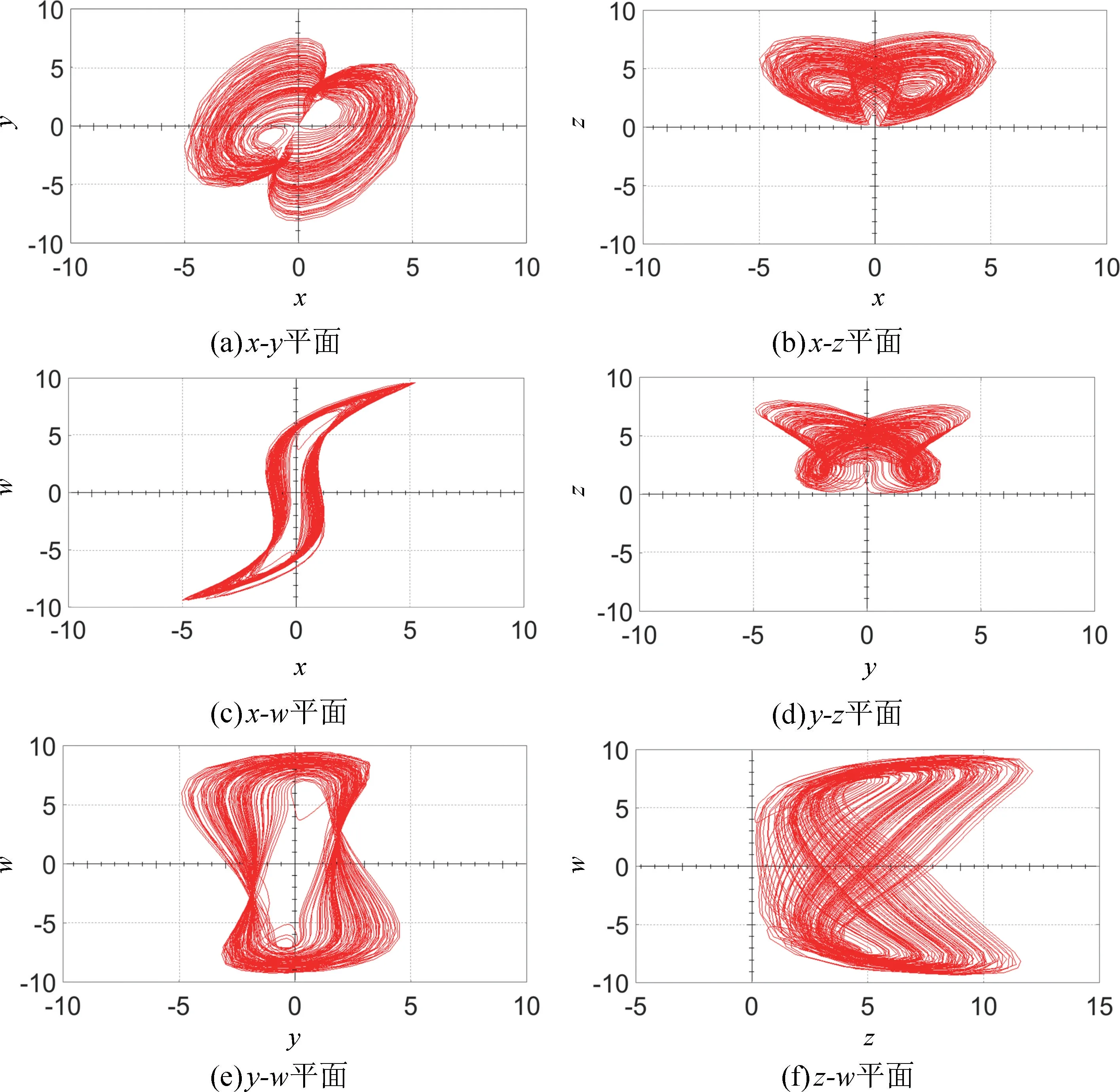
当系统(5)中参数为a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03,并设置系统初值为(x0,y0,z0,w0)=(0.1,0.1,0,0.1) 时,利用四维龙格-库塔算法,仿真得到系统(5)的相平面图,如图1 所示,由图可见,忆阻混沌系统(5)呈现出双涡卷混沌吸引子,该系统具有更复杂的吸引子结构。采用Jacobi 方法计算Lyapunov 指数谱如图2(a)所示,得出LE1=0.5108,LE2=0.0007,LE3=-2.0919,以及LE4=-11.4195,其中LEi,(i=1,2,3,4) 为系统的李雅普诺夫指数(Lyapunov Exponent)。系统四个状态变量的时域波形图如图2(b)所示;系统(5)的Lyapunov维数为DL=2.8616。由系统的相轨迹、时域波形图以及Lyapunov 指数与维数可知系统是混沌振荡的。
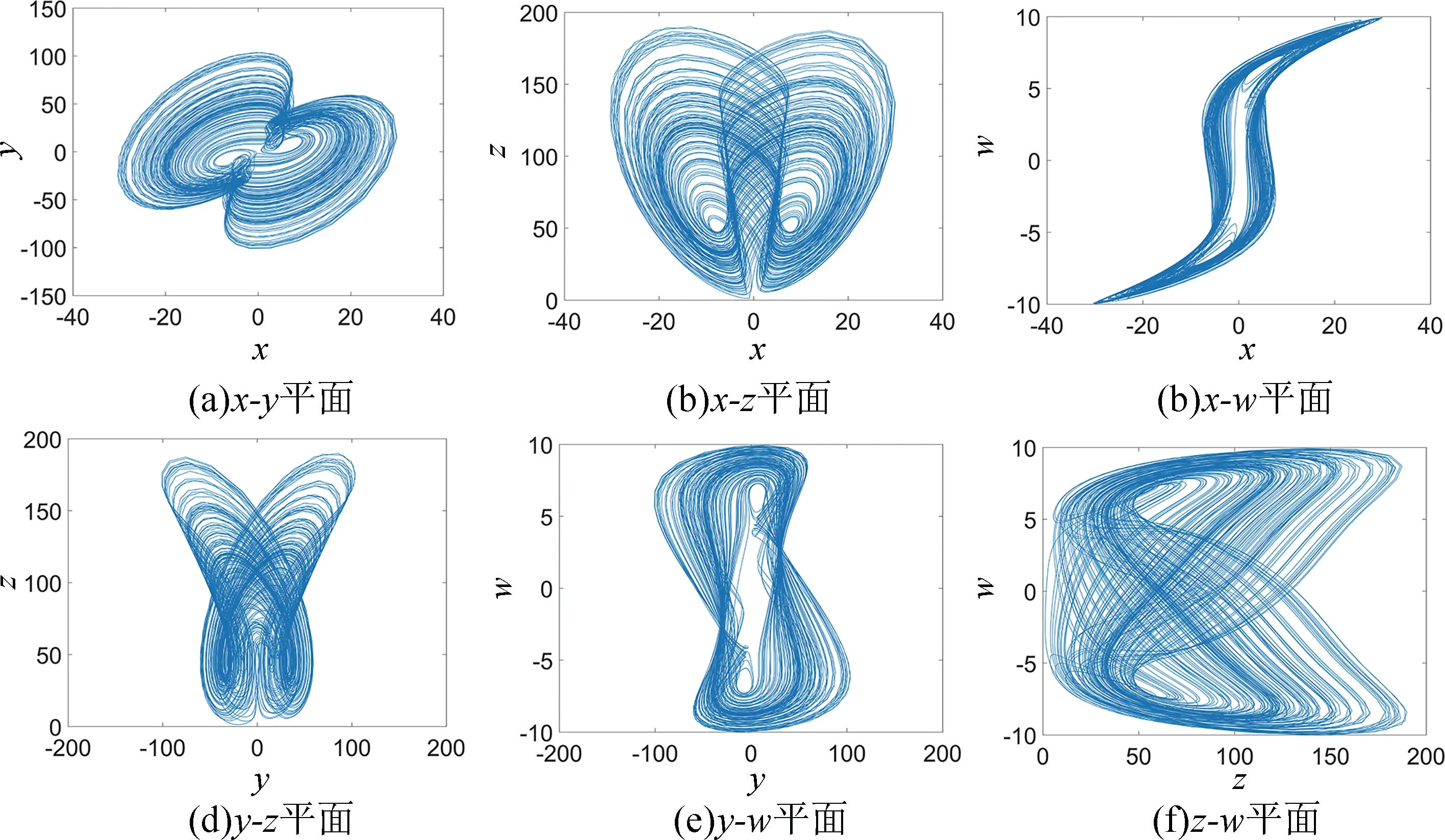
图1 系统参数为a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03,初值为(0.1,0.1,0,0.1)时的混沌吸引子相图Fig.1 The phase diagram of the chaotic attractor when the system parameters are a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03,and the initial value is (0.1,0.1,0,0.1)
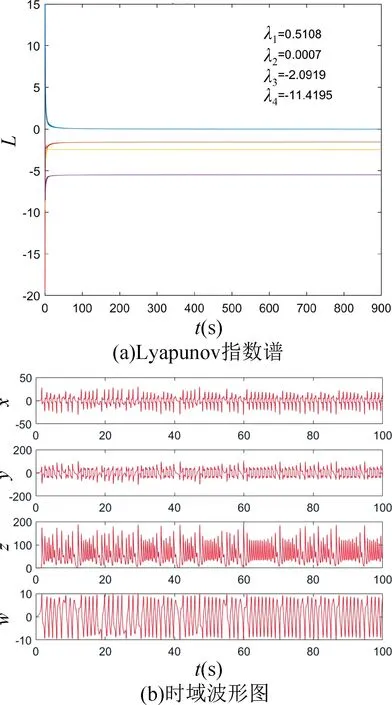
图2 系统参数为a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03,初值为(0.1,0.1,0,0.1)时的Lyapunov指数谱与时域波形图Fig.2 Lyapunov exponents spectrum and time domain waveform of the system with parameters are a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03 and initial values of (0.1,0.1,0,0.1)
2 动力学特性分析
2.1 耗散性
由系统(5)可得耗散度为:
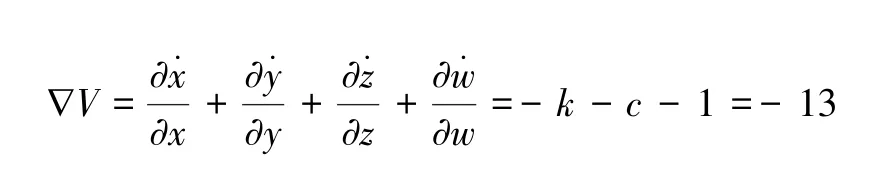
由∇V=-13<0 说明系统是耗散的,并以指数方式e-(k+c+1)dV/dt收敛,即系统在t时刻体积V0收缩为V0e-(k+c+1)。也就是说,当t→∞时,包括系统轨迹的每个体积元都会以指数形式收缩到0,即系统能够产生有界吸引子。
2.2 平衡点与稳定性
系统(5)的平衡点可以通过下列方程求解得到:

在此平衡点处线性化处理,可得系统的Jacobi矩阵:

由Routh-Hurwitz 稳定性判据可以得出系统在此平衡点处的稳定条件是:

在此平衡点处线性化处理,可得系统的Jacobi矩阵:

由Routh-Hurwitz 稳定性判据可以得出系统在此平衡点处的稳定条件是:

即得到此时系统的平衡点:

在此平衡点处线性化处理,可得系统的Jacobi矩阵:


由Routh-Hurwitz 稳定性判据可以得出系统在此平衡点处的稳定条件是:
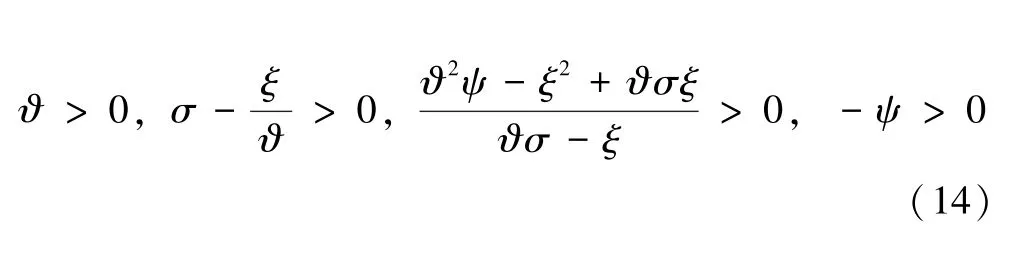
2.3 混沌特性
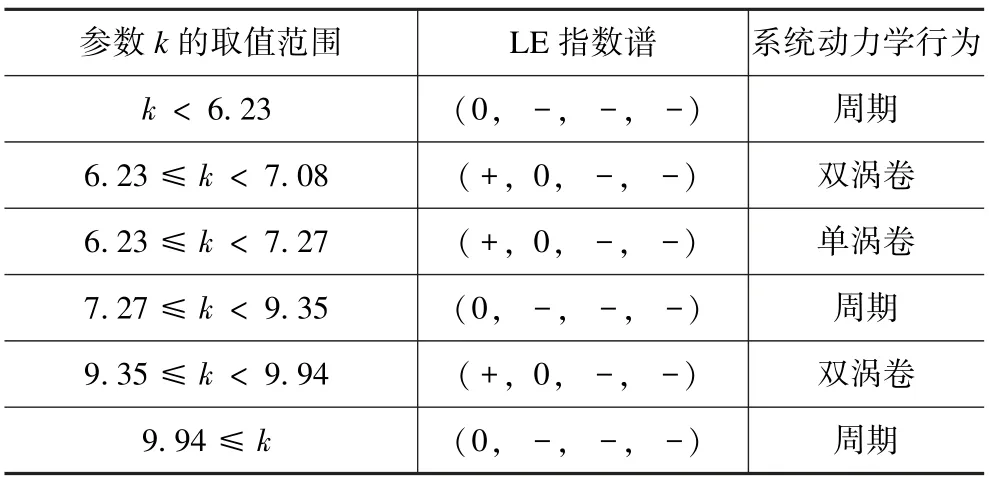
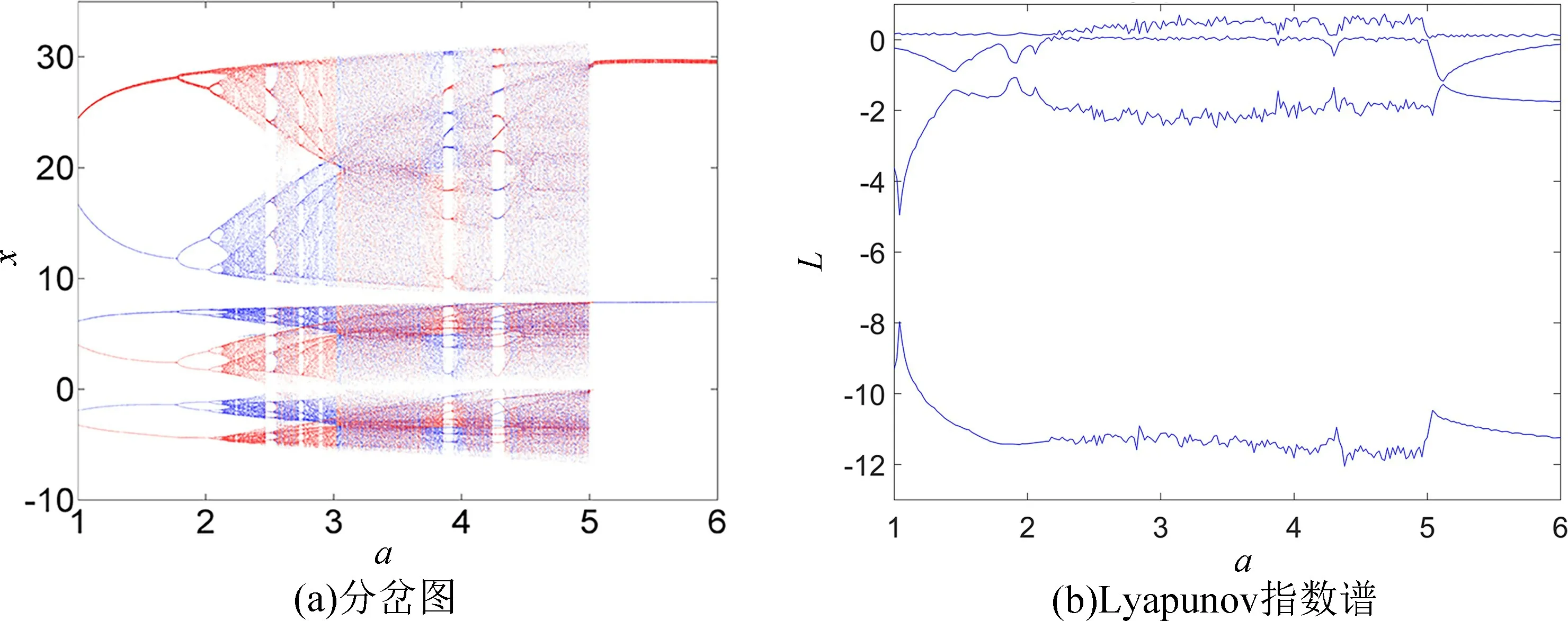
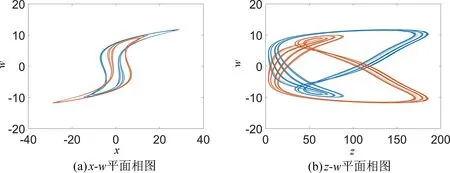
为了进一步研究系统的非线性动力学特性,系统(5)中的参数a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03,参数k∈[5,11],步长为0.01,初始状态(x0,y0,z0,w0)=(0.1,0.1,0,0.1),绘制其Lyapunov 指数谱及分岔图,如图3 所示。图3(a)揭示了系统(5)进入混沌的路径,随着参数k的增大,系统从周期态进入混沌态,在区间6.23 ≤k <7.08 和7.08 ≤k <7.27 内,系统产生双涡卷与单涡卷混沌吸引子,通过反倍周期分岔进入周期态,随后通过倍周期分岔进入混沌态,最后演化为周期态。根据图3(b)的Lyapunov 指数谱可进一步确定系统参数k对应的动力学行为,如表1 所列,部分动力学行为对应的吸引子相图如图4 所示。其中,图4(a)为参数k=8 时的系统相图,可见此时系统处于周期态,图4(b)为参数k=9.2 时的系统相图,此时系统处于混沌态,图4(c)为参数k=9.5时的系统相图,此时系统处于周期态,图4(d)为参数k=10.2 时的系统相图,此时系统处于周期态。
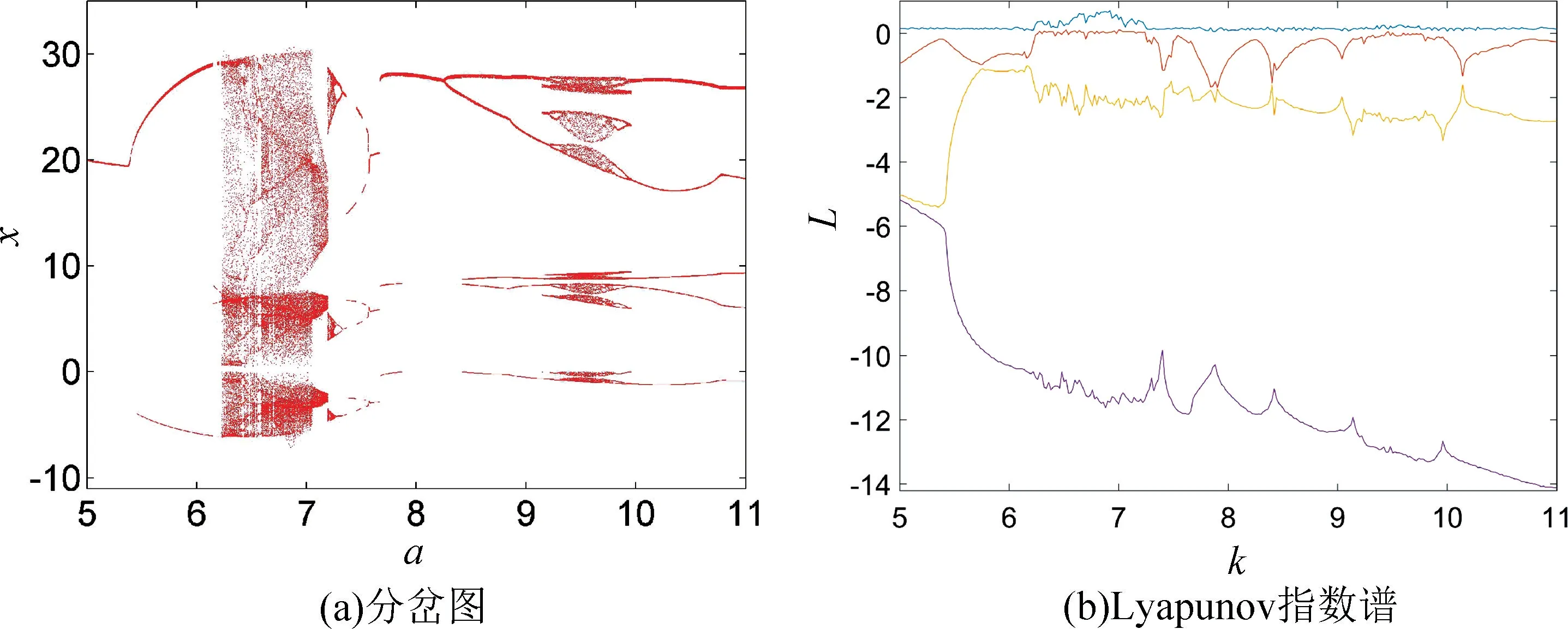
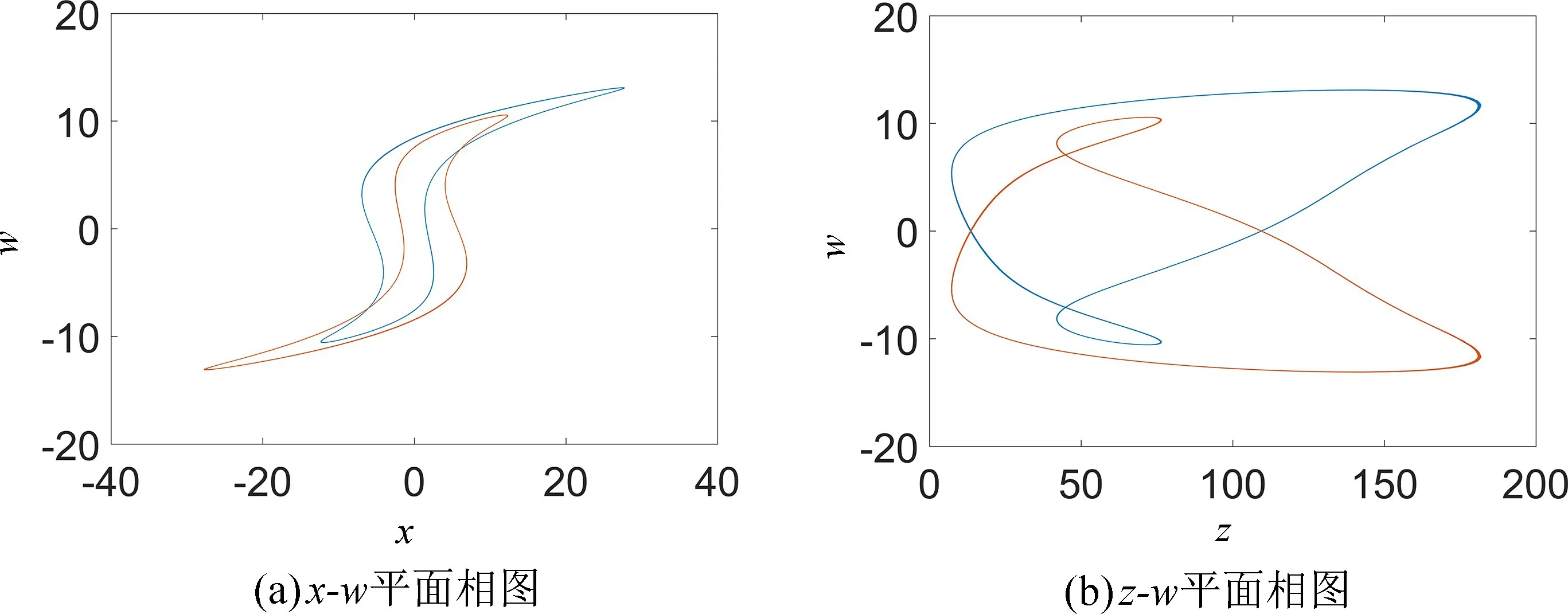
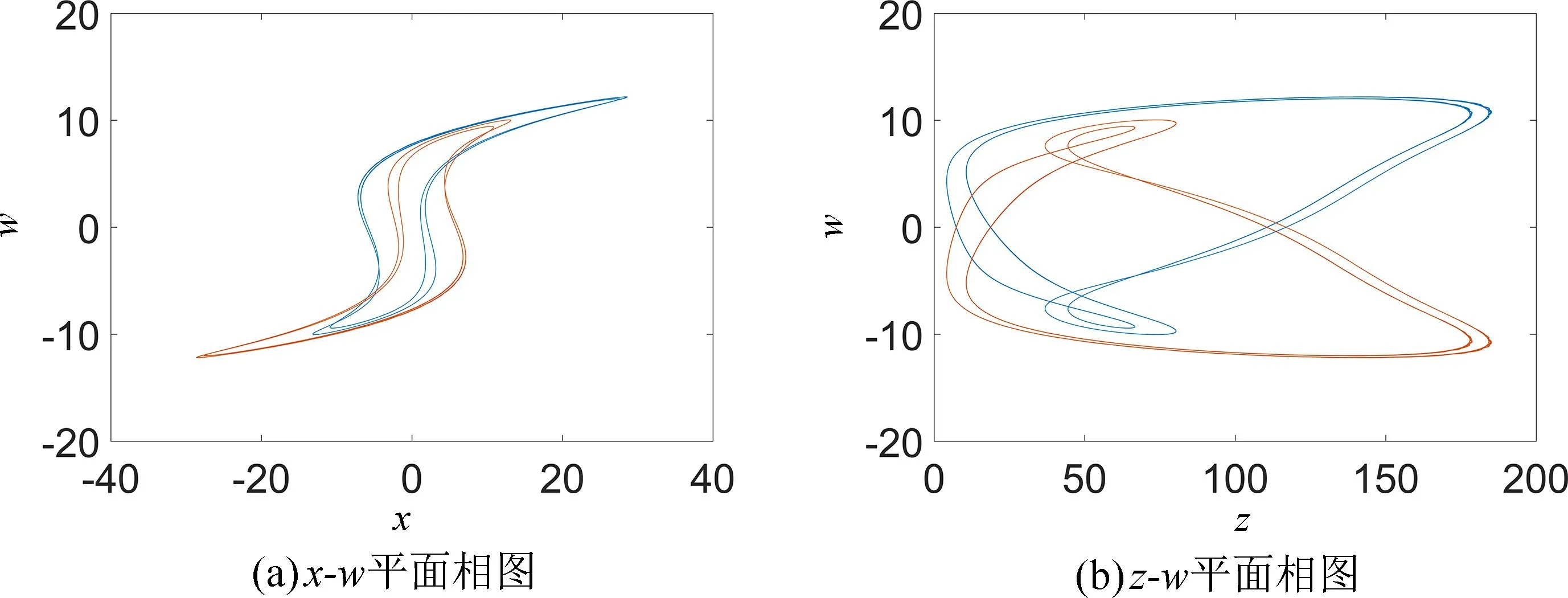
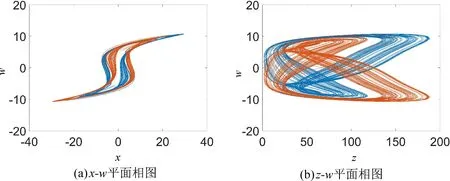
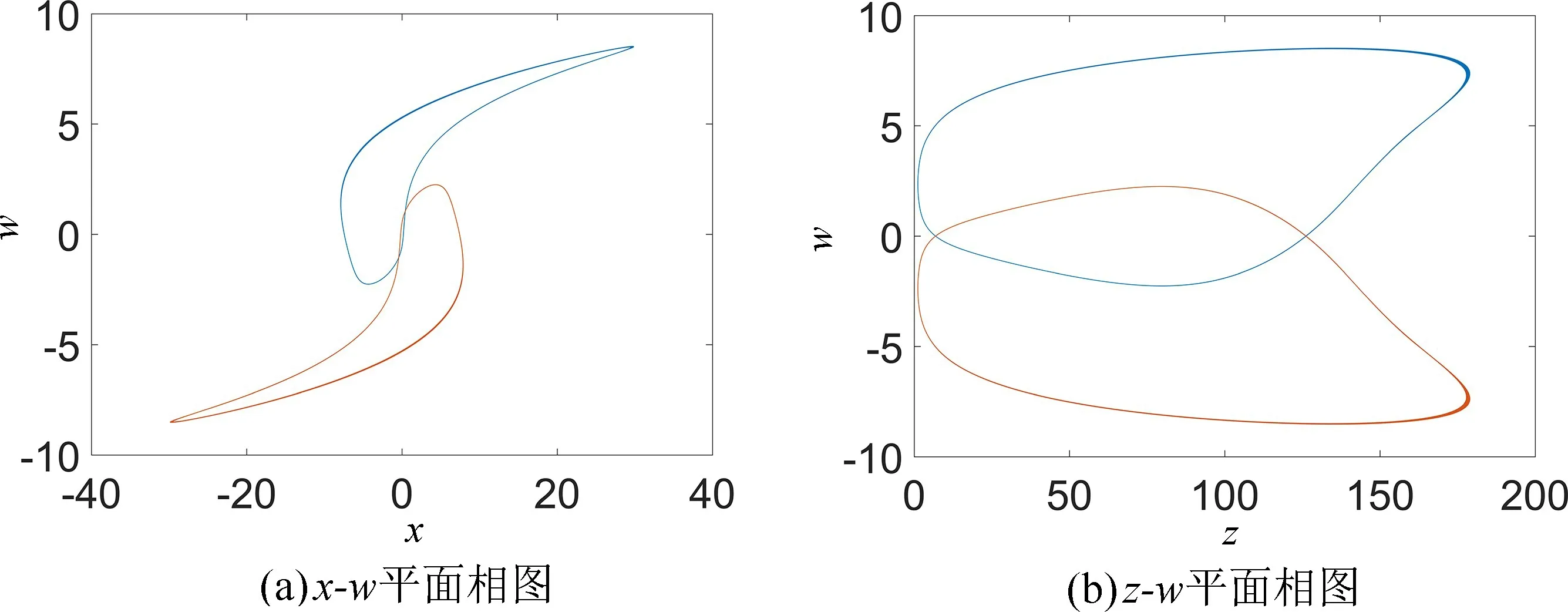
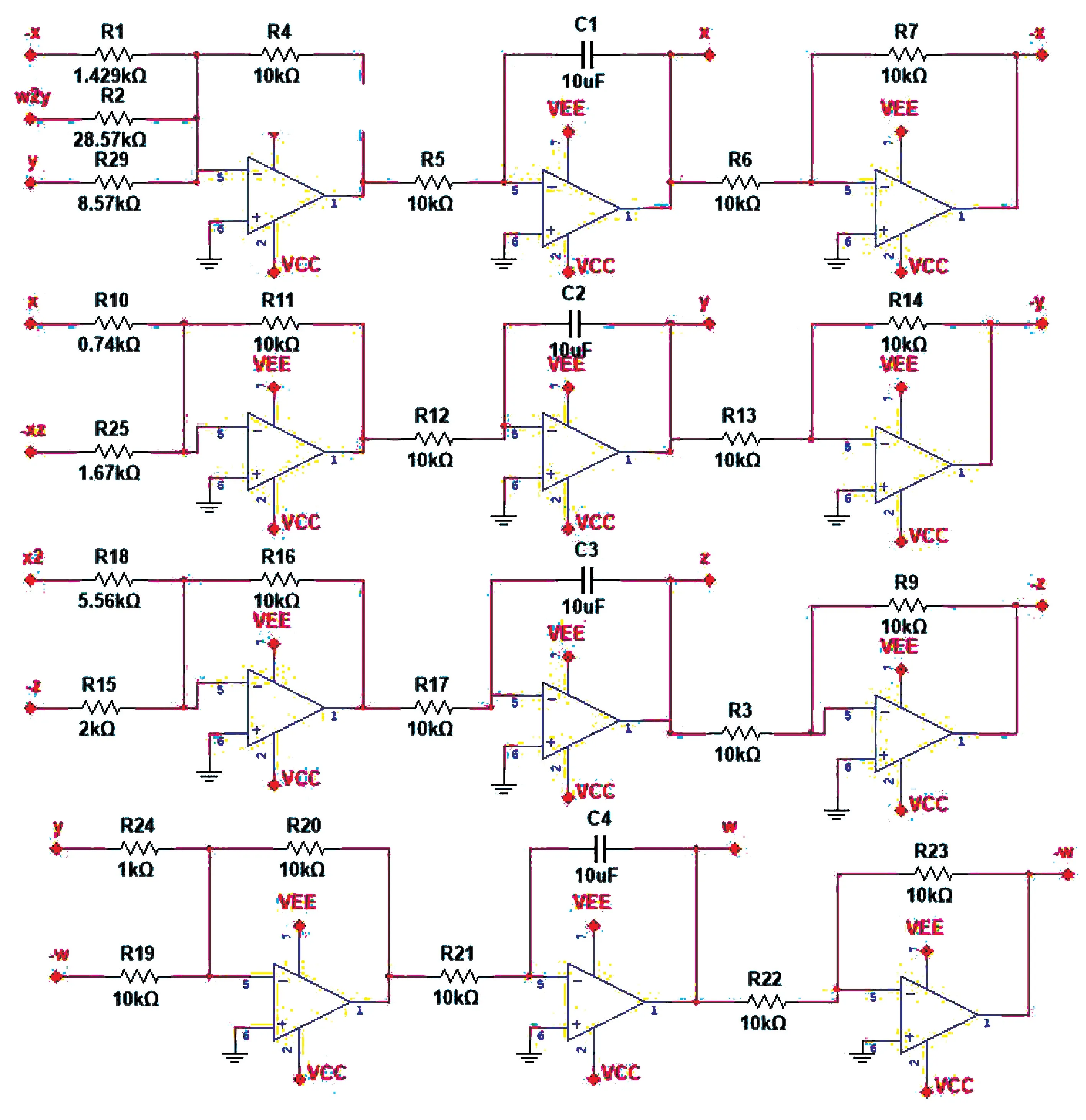
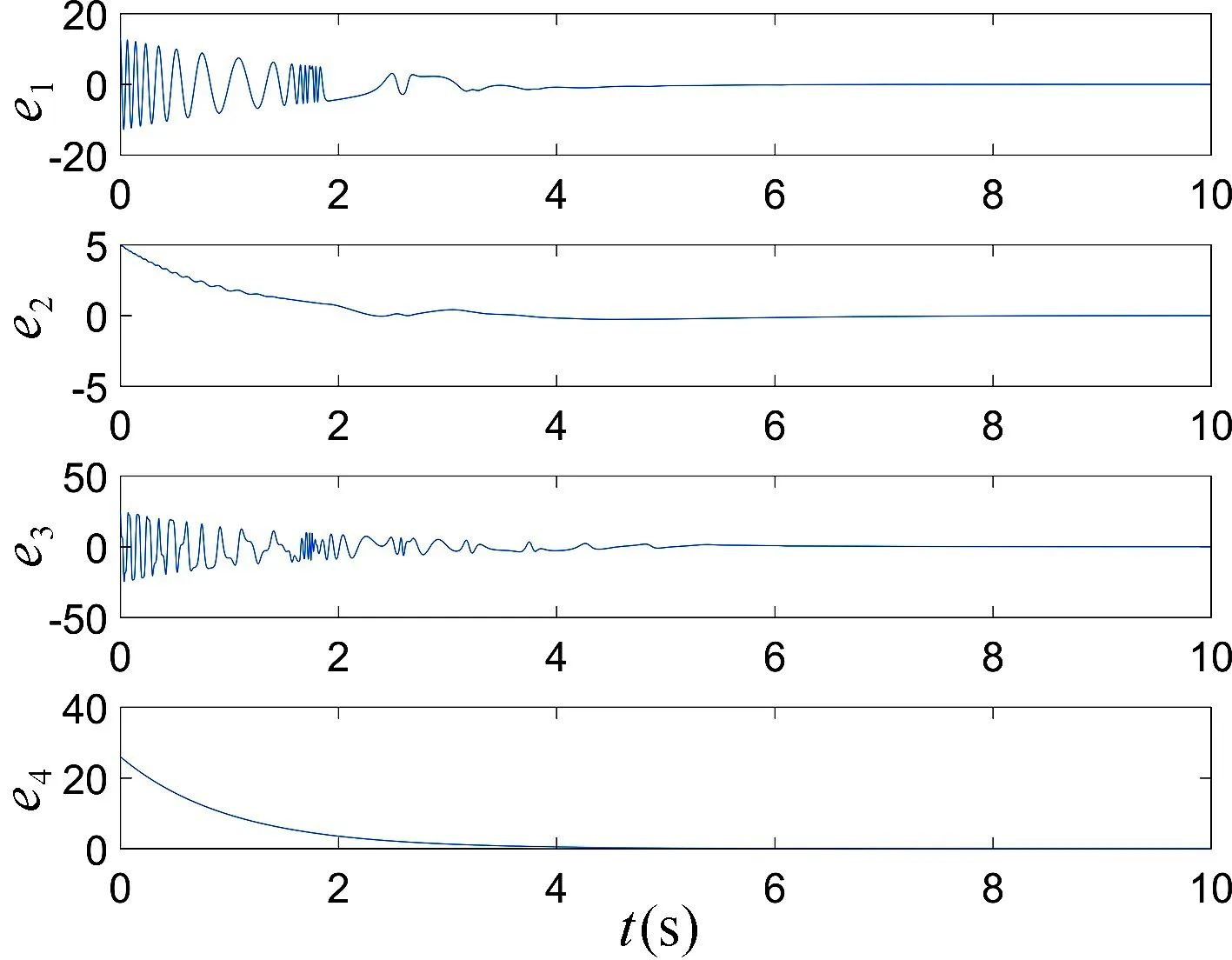
图3 当a=3.5,b=45,c=5,d=4,m=0.1,n=0.03,初值为(0.1,0.1,0,0.1)时,系统随参数5 图4 参数a=3.5,b=45,c=5,d=4,m=0.1,n=0.03 不变,初值为(0.1,0.1,0,0.1) 时,不同参数k对应的x-z 平面相图Fig.4 When the parameters a=3.5,b=45,c=5,d=4,m=0.1,n=0.03,the initial value is(0.1,0.1,0,0.1),the x-z plane phase diagram when the value of k is different 表1 当a=3.5,b=45,c=5,d=4,m=0.1,n=0.03,初值为(0.1,0.1,0,0.1),系统(5)随参数5 为进一步分析忆阻混沌系统(5)随着初始状态的变化而呈现的分岔和共存现象,固定系统(5)的参数a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03不变,取参数a∈[1,6],初始状态(x0,y0,z0,w0)分别选取(-0.1,-0.1,0,-0.1) 和(0.1,0.1,0,0.1),步长为0.005,其对应的随着参数a变化的Lyapunov 指数谱及分岔图如图5 所示,在图5(a)中,初值为(0.1,0.1,0,0.1) 的分岔图用红色表示,初值为(-0.1,-0.1,0,-0.1) 的分岔图用蓝色表示。图5(a)揭示了系统(5)进入混沌的路径,随着参数a的不断增大,系统通过倍周期分岔进入混沌态,会出现单涡卷、双涡卷吸引子以及周期态,最终演化为稳定态。根据图5(b)的Lyapunov 指数谱可进一步确定系统参数a对应的动力学行为。从图5 不难看出,共存周期态主要发生在区间 (1,2.2],[2.49,2.54),[4.34,4.345)和 [ 5.04,+∞)。在a=1.8 附近时系统由周期1 演变为周期2,此时选取a=1.5,在x-w和z-w平面可以观察到周期1 共存现象,如图6 所示,在a=2 附近时系统由周期2 演变为周期4,此时选取a=1.9,在x-w和z-w平面观察到周期2 共存现象,如图7 所示,在a=2.2 附近时系统由周期4 演变为混沌轨道,此时选取a=2.1,在x-w和z-w平面观察到周期4 共存现象,如图8 所示,在a∈(2.2,5.04) 时系统会出现单涡卷、双涡卷吸引子以及周期态现象,此时选取a=2.8,可以观察到混沌吸引子的共存现象,如图9 所示,在a >5.04 之后演变为稳定态,选取a=5.5,可以观察到稳定态的共存现象,如图10 所示。 图5 参数b=45,c=5,d=4,k=7,m=0.1,n=0.03 不变,不同初始值时,系统随参数1 图6 参数b=45,c=5,d=4,k=7,m=0.1,n=0.03 不变,参数a=1.5 时系统出现的周期1 共存现象,其中(蓝)初值为(0.1,0.1,0,0.1),(橙)初值为(-0.1,-0.1,0,-0.1)Fig.6 When the parameter are b=45,c=5,d=4,k=7,m=0.1,n=0.03,a=1.5,the coexistence of period attractor appear,in which the initial value of (blue) is (0.1,0.1,0,0.1),and the initial value of (orange) is (-0.1,-0.1,0,-0.1) 图7 参数b=45,c=5,d=4,k=7,m=0.1,n=0.03 不变,参数a=1.9 时系统出现的周期2 共存现象,其中(蓝)初值为(0.1,0.1,0,0.1),(橙)初值为(-0.1,-0.1,0,-0.1)Fig.7 When the parameter are b=45,c=5,d=4,k=7,m=0.1,n=0.03,a=1.9,the coexistence of period two attractors appear,in which the initial value of (blue) is (0.1,0.1,0,0.1),and the initial value of (orange) is (-0.1,-0.1,0,-0.1) 图8 参数b=45,c=5,d=4,k=7,m=0.1,n=0.03 不变,参数a=2.1 时系统出现的周期4 共存现象,其中(蓝)初值为(0.1,0.1,0,0.1),(橙)初值为(-0.1,-0.1,0,-0.1)Fig.8 When the parameter are b=45,c=5,d=4,k=7,m=0.1,n=0.03,a=2.1,the coexistence of period four attractors appear,in which the initial value of (blue) is (0.1,0.1,0,0.1),and the initial value of (orange) is (-0.1,-0.1,0,-0.1) 图9 参数b=45,c=5,d=4,k=7,m=0.1,n=0.03 不变,参数a=2.8 时系统出现的混沌吸引子共存现象,其中(蓝)初值为(0.1,0.1,0,0.1),(橙)初值为(-0.1,-0.1,0,-0.1)Fig.9 When b=45,c=5,d=4,k=7,m=0.1,n=0.03 and a=2.8,the chaotic attractors coexist in the system.The initial values of (blue) is (0.1,0.1,0,0.1) and (orange) is (-0.1,-0.1,0,-0.1) 图10 参数b=45,c=5,d=4,k=7,m=0.1,n=0.03 不变,参数a=5.5 时系统稳态共存现象,其中(蓝)初值为(0.1,0.1,0,0.1),(橙)初值为(-0.1,-0.1,0,-0.1)Fig.10 When the parameter are b=45,c=5,d=4,k=7,m=0.1,n=0.03,a=5.5,the steady-state coexistence of the system occurs,in which the initial value of (blue) is (0.1,0.1,0.1),and (orange) is (-0.1,-0.1,0,-0.1) 由于硬件实验中很难给定不同期望值时忆阻器的初始条件,为验证系统(5)的理论分析与数值仿真和复杂动力学行为,采用Multisim 电路仿真实现了该忆阻混沌系统。图11 为模拟仿真电路原理图,该电路由四路模拟运算电路组成,分别实现方程组(5)中状态x,y,z和w的运算。 图11 Multisim 模拟仿真电路原理图Fig.11 Schematic diagram of Multisim analog simulation circuit 通过四通道示波器得到的各相图如图12 所示,仿真结果与图1 所示的Matlab 数值仿真得到的混沌吸引子相图基本一致,从而验证了所提出的忆阻混沌系统的正确性。 图12 混沌吸引子Multisim 模拟仿真结果图Fig.12 Multisim simulation results of chaotic attractor 取忆阻混沌系统(5)为驱动系统,则响应系统为: 设受控响应系统与驱动系统间的状态误差为ex=x'-x,ey=y'-y,ez=z'-z,ew=w'-w,则由式(15)减去式(5)得到误差系统: 选取控制器ux,uy,uz和uw,使系统(16)零解渐近稳定,则混沌系统(5)和(15)完全同步。选取控制器ux,uy,uz和uw如下: 选取Lyapunov 函数为: 对式(19)求导,可得: 其中μ >0,η >0,当满足: 式(22)负半定。又因为式(19)是正定且递减的,所以误差系统(18)零解一致稳定。根据Barbalat's 推论,对任意初始条件均有ex(t),ey(t),ez(t),ew(t)∈L∞,即当t→∞时,ex(t),ey(t),ez(t),ew(t) →0,则误差系统(18)零解渐近稳定,从而系统(5)和系统(15)完全同步。因此有如下定理: 在控制参数以式(21)的形式变化的情况下,以控制形式(17)来控制响应系统(15),则响应系统(15)可与驱动系统(5)达到完全同步。 系统(5)中参数a=3.5,b=45,c=5,d=4,k=7,m=0.1,n=0.03,并设置驱动系统(5)初值为(x0,y0,z0,w0)=(0.1,0.1,0,0.1),响应系统(15)初值为=(13.1,5.1,25,26.1),即初始误差为(13,5,25,26),取步长为0.006,利用四维龙格-库塔算法在Matlab 上进行仿真,当对响应系统施加控制时,两系统状态之间的误差变化如图13 所示,响应系统中控制参数的变化如图14 所示。 图13 自适应控制下的误差曲线图Fig.13 Error curves diagram under adaptive control 图14 控制参数的变化曲线图,其中(红)为参数a,(蓝)为参数b,(绿)为参数c,(黑)为参数d,(青)为参数kFig.14 The change curves of control parameters,in which (red)is parameter a,(blue) is parameter b,(green) is parameter c,(black) is parameter d,(cyan) is parameter k 由图13 可见,在自适应控制下,初始误差为(13,5,25,26) 的情况下,两系统在t=5 附近达到同步。 本文构造了一个含有光滑三次型忆阻器的混沌系统。研究了该忆阻混沌系统随参数和初始状态变化的多种复杂动力学行为,数值仿真结果表明随参数的改变,系统共有两次进入周期态,且处于混沌状态的范围较大。随初始状态的变化,系统呈现周期共存、混沌吸引子共存以及分岔共存。为了验证系统的理论分析与数值仿真,用Multisim 进行了电路仿真,仿真结果与数值仿真基本吻合,验证了该电路的有效性,同时也为忆阻器混沌电路设计和电路实现提供一种新的思路。根据已有的自适应控制的理论分析和控制规则,设计了合适的自适应控制器,实现了未知参数时忆阻混沌系统的自适应同步,同时还可辨识出系统的未知参数,理论分析和数值仿真结果证实了所提出方法的准确性。设计的自适应控制器控制率连续,且不受系统参数的限制便可实施控制,使其在实际工程中更易于应用。由于硬件实验难以捕捉到混沌系统中多共存吸引子的异常动态行为,解决这一问题作为进一步研究的课题。
2.4 分岔与共存现象
3 忆阻混沌系统的电路实现
4 忆阻混沌系统的自适应完全同步
4.1 自适应同步
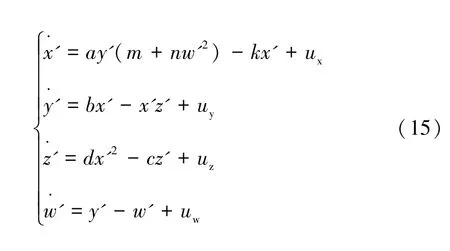
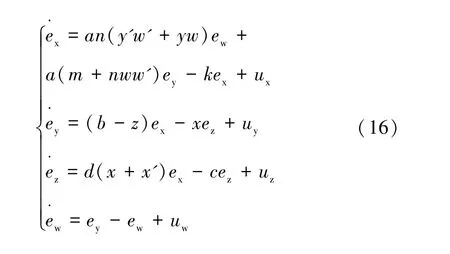



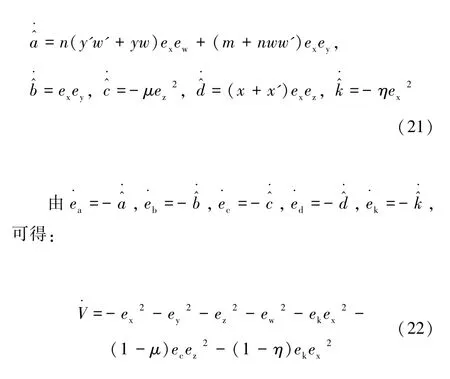
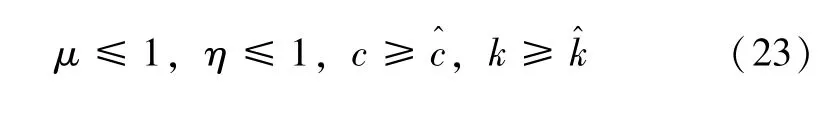
4.2 数值仿真

5 结论
