基于不完全重合信号的单快拍DOA 估计算法研究

曲明超，司伟建，袁雅芝

（1.哈尔滨工程大学信息与通信工程学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学先进船舶通信与信息技术工业和信息化部重点实验室，黑龙江 哈尔滨 150001）

1 引言

为了有效应对反辐射导弹（ARM,anti-radiation missile）的攻击，雷达有源诱偏技术日趋成熟，有源诱饵广泛应用在反辐射对抗中[1]。由于诱饵布阵位置、反辐射武器袭击的方向等不利因素影响，诱饵信号前沿和雷达信号前沿同时到达的有源诱偏系统很难实现，而且为了保护雷达，在时域上，通常有源诱饵信号的前沿会超前雷达信号的前沿0.1～0.2 μs[2-3]。

ARM、雷达和有源诱饵的部署如图1 所示。雷达和诱饵频率相同或接近，间距d通常为300～500 m，ARM 几乎同时接收到雷达和诱饵发射的电磁波信号，并对雷达和诱饵的合成信号进行（DOA,direction of arrival）估计，当ARM 不能分辨出雷达和诱饵时，会瞄准两者能量重心进行攻击，攻击路线为S。2 个辐射源在角度间隔为θ时被区分开，ARM 以最大过载向其中一个目标引导攻击，攻击路径为S′，提高ARM 的角分辨性能和估计精度可以降低ARM 的脱靶概率。

图1 ARM、雷达和有源诱饵的部署示意

传统的反辐射导弹通过比幅比相法或干涉仪的方法进行测向，但其仅适用于单目标测向且测向精度有限。多重信号分类算法等子空间类算法[4]利用子空间的正交性估计入射信号的来波方向，但在低信噪比和低快拍数情况下估计性能急剧下降，而且子空间类算法要求入射信号之间互不相关，但由于敌方干扰和多径等因素影响，相关信号是不可避免的。针对这些问题，文献[5-7]将稀疏表示理论应用在DOA 估计中，显著改善了算法在低信噪比时的估计性能，但算法复杂度较高，不符合工程中实时性要求。

为了利用诱饵信号前沿会超前雷达信号前沿这一先验信息以提高算法的分辨能力，文献[8]利用雷达和诱饵时序不一致构成不完全重合信号的特点，提出了适用于标量阵列下的TI-ESPRIT 算法，在低信噪比和小快拍数情况下有更好的估计效果，但该算法仅适用于标量阵列。文献[9]利用斜投影技术，可以去除先验信息的影响，提高算法的分辨能力，但该算法在信号相关时会失效。

由于诱饵信号前沿只有0.1～0.2 μs，此时阵列接收数据极其有限，要利用诱饵信号前沿会超前雷达信号前沿这一先验信息，就对小快拍测向提出了要求。单快拍测向是小快拍测向极限，单快拍测向可以通过减少采样数据点数降低资源消耗、提高算法实时性，也是当前的一个研究热点，学者们在多快拍DOA 基础上提出了很多有实用价值的单快拍DOA 估计。文献[10]对空间平滑算法进行改进，提出了一种基于单快拍的改进的空间平滑算法，提高了阵列孔径，可以利用单快拍数据进行测向。文献[11-12]仅利用阵列接收的一次快拍数据重构伪协方差矩阵，实时性好，对构造的伪协方差矩阵分解得到噪声子空间和信号子空间，并且不受信号之间相关性的影响，能够实现对相干信号的估计，但对信噪比要求较高，低信噪比情况下其性能急剧下降。文献[10-12]所提算法都是基于标量阵列的单快拍DOA 估计算法，无法适用于极化敏感阵列的单快拍DOA 估计。文献[13]提出了极化域平滑解相干算法（PSA,polarization smoothing algorithm），相对于空域平滑解相干算法，其有效孔径在平滑处理后没有损失，但极化域平滑算法在单快拍情况下估计性能急剧下降。文献[14]利用空域平滑的思想，在极化域中提出了一种单快拍的极化域平滑算法（SS-PSA,single snapshot PSA），该算法可以利用单快拍数据对极化敏感阵列下的相干信号进行估计，算法复杂度低，但该算法在低信噪比情况下估计效果差。

本文利用诱饵信号和雷达信号是不完全重合信号的特点，在单快拍的极化域平滑算法基础上，提出了基于不完全重合信号的单快拍DOA 估计算法，该算法仅利用单快拍数据，实时性好，对间隔很近的相干信号有更好的分辨能力。

2 信号模型

考虑由M个极化敏感阵元组成的均匀线阵，极化敏感阵元是沿x轴方向和y轴方向的2 个偶极子组成的正交偶极子对。天线阵列以原点为参考阵元，沿x轴正向均匀排布，阵元间距为λ/2，如图2所示。

图2 极化敏感阵列示意

假设在阵列远场处有K个窄带完全极化波点源信号，信号入射平面为xoy平面，第k个信号方位角为θk，极化辅助角和极化相位差分别为γk和ηk。方位角θk∈[0,π]，极化辅助角γk∈[0,π/2]，极化相位差ηk∈[ -π,π]。假定阵列接收到的噪声为圆空−时−极化白噪声，且噪声与信号之间统计独立，则t时刻阵列接收信号矢量可表示为

其中，使用的矩阵索引语法为MATLAB 的矩阵索引语法；X(t)为M× 1维的阵列接收数据矢量；S(t)为K× 1维空间信号矢量；N(t)为M× 1维的噪声数据矢量；A为阵列的M×K维导向矢量阵。

将式(3)代入式(1)可得

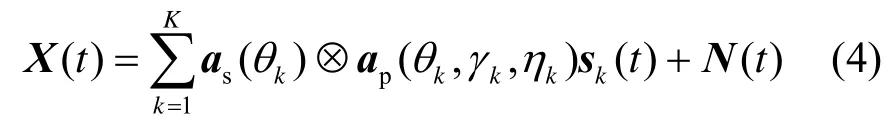
其中，⊗为克罗内克积。以坐标原点为参考点，第k个信号入射到天线阵列所在空间直角坐标系的传播矢量为r=[cosθk,sinθk,0]T；各阵元所在坐标位置矢量为lm，第k个信号的空间导向矢量为

ap(θ k,γ k,ηk)为极化−角度域导向矢量，对于正交偶极子对阵元，其可以表示为

对于本文中的均匀线阵，由于信号入射平面为xoy平面，式(6)可写为

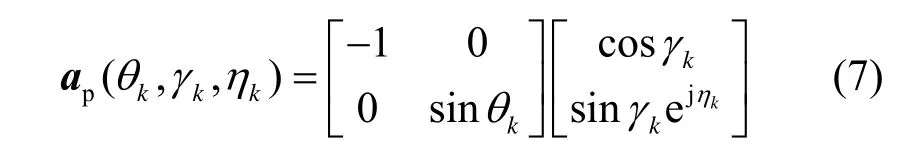
3 算法原理与分析

3.1 极化敏感阵列的单快拍的DOA 估计算法

若将空间阵列中沿x轴和沿y轴的M个偶极子分别构成一个均匀线阵，则如图2 所示的阵列可以划分为2 个极化−角度域匹配的子阵，利用这一特点可以实现极化域平滑。将阵列输出信号矢量的顺序进行调整，可得

为方便描述，阵列输出信号矢量和噪声矢量仍用X(t)和N(t)表示，且式(8)中各符号定义与式(4)完全相同。

第k个子阵的观测矢量Xk(t)可构造为Xk(t)=JkX(t)，其中

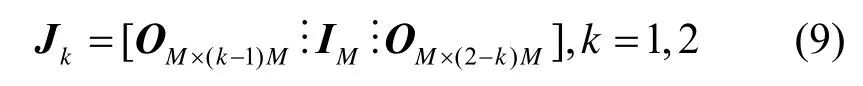
其中，M为极化敏感阵元数量。

将阵列接收数据矢量重新排列，得到新的阵列接收数据矢量为

依据文献[14]的推导过程，新的阵列接收数据矢量可表示为

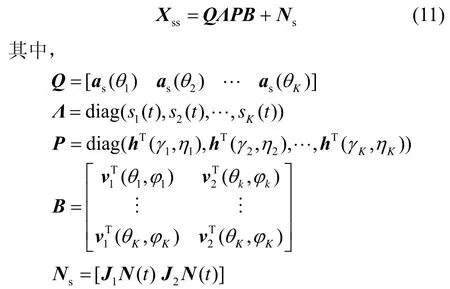
v1和v2分别为v的第一行和第二行。

利用空间共轭复制技术，构造一个共轭复制增广矩阵Xaug为

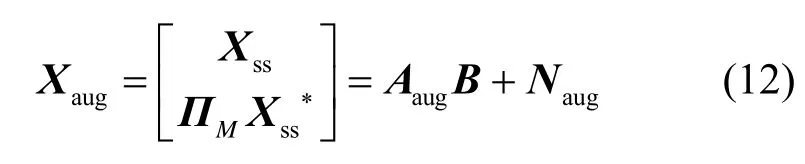
对Xaug按照前后向平滑的思想进行处理可得

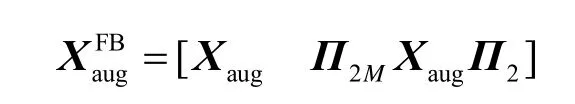
3.2 不完全重合信号的单快拍DOA 估计算法

由于雷达信号和诱饵信号构成了不完全重合信号[8]，可以利用协方差相减的思想，提高算法的估计性能。假设数据被分为两段，第一段包含L个辐射源，第一段包含的信号源为SL（t）；第二段共包含K个辐射源（其中第一段的L个辐射源在第二段中也存在），第二段包含的两部分信号源分别为SL（t）、SD（t），K、D、L满足D=K-L关系。若第二段包含的K个辐射源频率相同且采样时间相同，则这K个辐射源是相干的。对式(8)中接收数据矢量X(t)进行准确分段，对分段后的接收数据矢量重新排列，式(10)中重新排列的接收数据可表示为

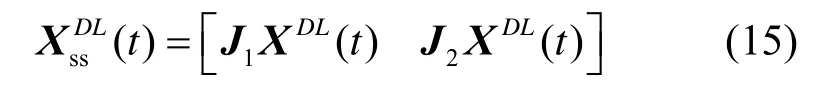
其中，

其中，AD和AL分别为阵列流型矢量中不同的D列和L列；XDL(t)为阵列接收到D+L个信号的数据；XL(t)为阵列接收到L个信号的数据。

当只有L个信号入射时，式(10)中重新排列的接收数据可表示为

将式(15)和式(16)相减，可得

其中，ND(t)表示2 个噪声数据矩阵相减后的结果，若噪声统计特性不变，则其为零矩阵。同式(16)，可得只有D个信号入射的重新排列数据矩阵，即

本文算法通过共轭复制增广矩阵相减能提高算法的估计性能，这是因为在共轭复制增广矩阵相减的过程中，减少了噪声对剩余D个信号的影响。而且通过共轭复制增广矩阵相减，将K个信号的DOA 估计转换为对D个信号和L个信号的DOA 估计，有利于提高算法的分辨角。

基于不完全重合信号的单快拍极化平滑DOA估计算法步骤如下。

1) 从t时刻的阵列接收数据矢量X(t)，构造新的阵列接收数据矢量为

2) 构造t时刻的虚拟增广矩阵Xaug为

3) 对虚拟增广矩阵进行差分，计算每段信号的虚拟增广矩阵，然后对每段信号的虚拟增矩阵执行步骤4)～步骤7)，计算每段信号的DOA 估计值。4) 对虚拟增广矩阵进行前后向平滑，构造为

6) 通过最小二乘估计的方法得到矩阵Ψ0，令则

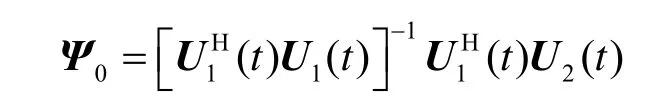
7) 对Ψ0进行特征值分解，求特征值对应相位即对应相位时延，转换可求出信号DOA。

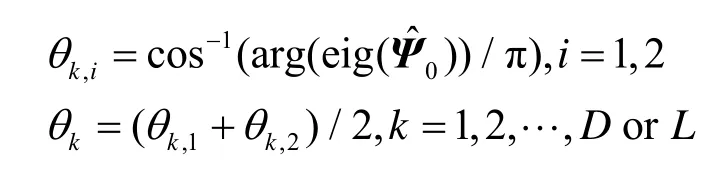
3.3 计算量分析与比较

本文对各种算法计算复杂度进行分析时，由于乘法运算的计算量远大于加法运算的计算量，因此不考虑加减法运算的计算量。下面对PSA 和不完全重合信号的单快拍DOA 估计算法的各部分进行分析，以比较其算法复杂度的区别。

极化域平滑解相干算法各步骤运算量如表1 所示，主要包括以下几个部分。

表1 极化域平滑解相干算法各步骤运算量

1) 计算单快拍的阵列接收数据协方差矩阵R需要复数乘法次数为M2I，M为阵元数，I为子阵数量，本文中I取值为2。

2) 对埃尔米特矩阵R进行特征值分解，采用二阶主子阵实数化法与Jacobi 方法相结合的特征值分解方法不仅精度高而且实时性好[15]。特征值范分解的运算量与遍历的次数有关，当遍历次数为4 时，复数乘法运算量约为20M3-20M2。

3) 谱峰搜索的运算量与搜索步长紧密相关，计算每个谱峰点所需的复数乘法为M3/2 +2M2+39M，若方位角搜索范围为30°～150°，搜索步长为1°，搜索点数为121。

通过表1 可以发现，谱峰搜索的点数决定了极化域平滑解相干算法的总的运算量。虽然可采用大步长进行粗搜索，小步长进行精搜索的方法降低极化域平滑解相干算法的搜索点数，但这种方式在多个信源同时存在时不适用，采用大步长进行搜索容易将多个信号的谱峰进行融合，导致其估计错误。

在相同阵元数条件下，虚拟极化域平滑解相干算法构造的信号矢量长度是极化域平滑解相干算法构造的信号矢量长度的2 倍，因此可将表1 中的M用2M代替，估算出虚拟极化域平滑解相干算法的运算量大致是极化域平滑解相干算法的4 倍。虚拟空域平滑算法构造的信号矢量长度是极化域平滑解相干算法构造的信号矢量长度的4 倍，因此可将表1 中的M用4M代替，估算出虚拟空域平滑算法的运算量大致是极化域平滑解相干算法的25 倍。

不完全重合信号的单快拍DOA 估计算法运算量如表2 所示，主要包括以下几个部分。

表2 不完全重合信号的单快拍DOA 估计算法运算量

当阵元数M为7，信号数量K为2 时，根据表1和表2 中的各步骤运算量，可得本文算法的计算量是极化域平滑解相干算法计算量的19%，是虚拟极化域平滑解相干算法计算量的5%。

4 仿真验证

考虑由正交偶极子对组成的均匀线阵，阵元间隔d=λ/2，正交偶极子对沿x轴正向均匀排布，偶极子指向为沿x轴方向和沿y轴方向，考虑窄带远场相干信号个数为2，相干系数g=exp(jπ/4)。

4.1 信噪比对算法估计性能影响

考虑由7 个正交偶极子对组成的均匀线阵，假设在远场处2 个窄带等功率的点源入射到阵列上，且阵列对信号单快拍取样，搜索步长为1°，为了避免信号方位角落在搜索网格点上，信号的方位角参数设置为(70.5°,115.5°)，极化参数(γ,η)分别为(20°,30°) 和(70°,120°)，信号频率为3.5 GHz。进行1 000 次蒙特卡罗仿真，将本文算法与虚拟极化域平滑算法、虚拟空域平滑算法、极化域平滑的ESPRIT（PS-ESPRIT）算法对比。信噪比对正确分辨概率和均方根误差的影响分别如图3 和图4 所示。

图3 信噪比对正确分辨概率的影响

从图3 和图4 可以看出，在低信噪比情况下，本文算法有更好的分辨概率和均方根误差，由于本文算法对构造的共轭复制增广矩阵进行相减，使噪声的影响降到最小，因此在低信噪比情况下有更好的估计性能。

图4 信噪比对均方根误差的影响

4.2 角度间隔对算法估计性能影响

假设在远场处2 个窄带等功率的点源入射到阵列上，且阵列对信号单快拍取样，其中一个信号的方位角固定在90.5°，另一个信号的方位角由91.5°增加到120.5°，信噪比为5 dB，其他条件与4.1 节实验保持一致。为了验证算法估计性能，进行了1 000 次蒙特卡罗仿真，将本文算法与虚拟极化域平滑算法、虚拟空域平滑算法、PS-ESPRIT 算法对比。角度间隔对正确分辨概率的影响如图5 所示。

图5 角度间隔对正确分辨概率的影响

从图5 中可以看出，当2 个信号源的间隔达到3°时，本文算法对2 个信号的正确分辨概率就可以达到80%，远高于其他算法的正确分辨概率。一方面是由于本文算法对构造的共轭复制增广矩阵进行相减，使噪声的影响降到最小；另一方面在相减的过程中，减少了每次待估计的信号的数量，因此在很小的角度间隔下也有很高的正确分辨概率。

4.3 阵元数量对算法估计性能影响

假设在远场处2 个窄带等功率的点源入射到阵列上，且阵列对信号单快拍取样，信号的方位角参数为(90.5°,110.5°)，极化参数(γ,η)分别为(20°,30°) 和(70°,120°)，信号频率为3.5 GHz，信噪比为5 dB。进行1 000 次蒙特卡罗仿真，将本文算法与虚拟极化域平滑算法、虚拟空域平滑算法、PS-ESPRIT 算法对比。阵元数量对正确分辨概率和估计均方根误差的影响分别如图6 和图7 所示。

图6 阵元数量对正确分辨概率的影响

图7 阵元数量对估计均方根误差的影响

从图6 和图7 中可以看出，随阵元数量的增加，估计均方根误差呈降低趋势，本文算法的均方根误差始终比虚拟空域平滑算法和虚拟极化平滑算法低。由于PS-ESPRIT 算法不使用谱峰搜索，通过求解一个凸优化问题得到信号的DOA 估计结果，因此PS-ESPRIT 算法估计精度劣于虚拟空域平滑算法和虚拟极化平滑算法，本文算法对构造的共轭复制增广矩阵进行相减，减小了噪声的影响，估计精度和估计正确概率要优于其他算法。

4.4 快拍累积对算法估计性能影响

假设在远场处2 个窄带等功率的点源入射到阵列上，信号的方位角参数为(90.5°,110.5°)，极化参数(γ,η)分别为(20°,30°) 和(70°,120°)，信号频率为3.5 GHz，信噪比为5 dB，快拍数为5。为了验证算法估计性能，进行1 000 次蒙特卡罗仿真，将本文算法与虚拟极化域平滑算法、虚拟空域平滑算法、PS-ESPRIT 算法对比。快拍累积对正确分辨概率和估计均方根误差的影响分别如图8 和图9 所示。

图8 快拍累积对正确分辨概率的影响

图9 快拍累积对估计均方根误差的影响

分析图8 和图9 可得，通过多次采样对阵列接收信号进行累积，可以降低噪声影响，提高信噪比。虽然本文算法适用于单快拍，但在阵列接收数据极其有限却不为单快拍时，由于本文算法对信号形式没有限制，可以使用不同时间采样点的数据，快拍的累积可以降低噪声的影响，因此在短快拍时本文算法理论上依然有很好的估计性能。本节对信噪比为5 dB、5 次快拍累计情况下算法性能进行仿真，仿真结果与分析一致，证明快拍累积有利于本文算法的估计性能。

5 结束语

本文根据有源诱饵信号和雷达信号在频域上相同或接近，在时域上有源诱饵信号超前雷达信号等特征，提出了一种基于不完全重合信号的单快拍DOA 估计算法。仿真结果表明，该算法在低信噪比和较少阵元数情况下有更优越的估计性能，而且本文算法可以分辨角度间隔达到3°的2 个信号。虽然本文算法基于单快拍数据，但快拍的累积有利于提高算法估计性能。由于该算法在单快拍情况下通过求解凸优化问题得到信号DOA 估计结果，不需要进行谱峰搜索，算法实时性好，适用于雷达、ARM等阵列天线系统接收数据有限的应用场景。