扩压叶栅缩放模化中表面粗糙度的影响及其修正方法*
2022-01-11王英杰
王英杰 胡 磊 戴 韧
(1.上海电气燃气轮机有限公司;2.上海理工大学 能源与动力工程学院;3.上海电气电站设备有限公司)
0 引言
基于相似原理的模化设计与试验是叶轮机气动设计与性能验证的基本方法。模化叶轮的几何尺寸按比例缩放,保持流动的马赫数与原型一致,而此时模化叶轮的流动雷诺数与母型不同。另一方面,在用叶栅实验模拟实际表面恶化对气动性能的影响时,表面粗糙度也难以与母型保持一致。因此,需要综合考虑流动雷诺数、表面粗糙度对叶型性能的影响,并且建立模化叶轮与母型之间的性能修正关系。
董帆[1]分析了离心风机相似模化设计时引起误差的主要因素,并设计了修正算法。李富成[2]基于通风机全压公式和摩擦阻力损失公式,并结合尼库拉茨半经验公式,推出了不同的流道表面相对粗糙度下模型与实物流动效率之间的计算公式。
在压气机流动研究中,Bons[3]总结粗糙度效应与流动雷诺数、粗糙度大小以及进口马赫数均有关。雷诺数和粗糙度通过影响边界层转捩[4]、分离[5]以及湍流区的摩擦效应影响边界层的发展,进而影响流动损失。Leipold[6]等人在NACA65 K48叶栅实验中发现,随着雷诺数提高,粗糙度效应更加明显,总压损失增大,且不同冲角下表面粗糙度对流动边界层发展的影响存在差异。Bammert[7]研究雷诺数为4.3×105的低速压气机叶栅发现,增加粗糙度,叶型损失从2%增加到10%。高磊[8]对不同粗糙度及攻角下的低速压气机叶栅研究发现,粗糙度对叶栅性能的影响存在一个粗糙度值的敏感区,而敏感区域与来流Re和攻角均有关,Re越高,攻角越向正攻角偏移,其下临界值越小。
分析表面粗糙度和雷诺数对压气机性能影响的基本方法是基于管内流动与平板边界层理论。定义两个临界雷诺数,将流动分为三个区域,建立流动损失的修正关系。Schaffler[9]揭示了表面粗糙度和雷诺数对多级轴流压气机影响规律。Sturb[10]引入摩擦因子,对于同一台离心压气机,在车间实验和特定条件下,提出了雷诺数变化时流动损失的修正方法。Syverud[11]引入了“等效雷诺数”的概念,提出了轴流压气机表面恶化时流动损失的修正方法。Casey[12]从基于耗散损失的多变效率表达式出发,对损失项进行分解,将压气机中与雷诺数相关的损失规律类比于平板流动损失规律,推导出当压气机来流雷诺数或粗糙度相对于参考条件发生变化时的多变效率。以上工作都是基于同一模型,研究不同雷诺数或表面粗糙度的影响,而没有涉及和验证因几何缩放造成的两个因素的共同作用。
本文将用数值计算模拟压气机叶型缩放过程中,表面粗糙度和流动雷诺数对叶型性能的综合影响。首先基于等效粗糙度模型,确定叶型损失与平板表面摩擦因子间的关系,建立修正关联式。其次考虑到扩压叶栅逆压梯度流动的特性,对叶型损失进一步修正。最后考虑了攻角影响,建立一套压气机叶栅模化问题中叶型损失的修正方法。
1 叶栅模型与数值方法
本文研究对象为NACA-65叶型,如图1所示。叶栅设计参数及几何参数稠度C/t=0.68,弯角ω=26.4°,安装角βs=30°,进口马赫数Ma1=0.5。以弦长50mm 的叶型作为模化试验叶型,在保持流动马赫数相似的条件下,变动叶栅弦长,模拟叶栅流动雷诺数的影响。叶栅性能分析采用ANSYS CFX 求解器求解三维、定常RANS 方程,湍流模型为耦合γ-Reθ,转捩模型的SST模型。进口给定速度大小、方向与湍流度,出口给定平均静压,保证进口Ma1=0.5。设置壁面绝热无滑移,周向为周期性边界条件。

图1 NACA-65 叶型Fig.1 NACA-65 blade profile
本文使用Poinwise 生成网格,采用O4H 拓扑结构,计算域进口和出口分别距前缘、尾缘1.5倍和2倍轴向弦长。对近壁面处边界层网格加密,经网格无关性验证,如图2 所示,当第一层网格高度为y=0.01mm,拉伸比为1.1,单层网格数为6.4 万时,满足网格无关性要求,此时网格正交性大于50°,Y+<1。
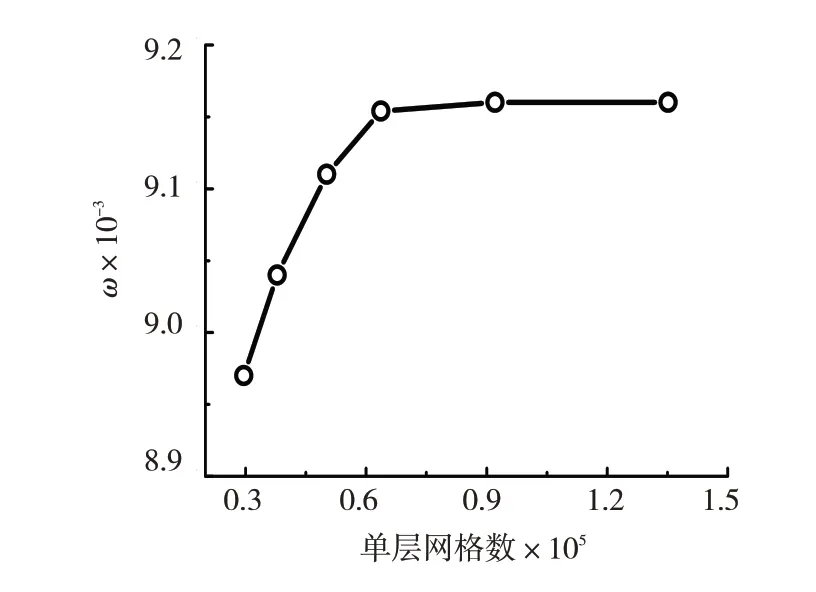
图2 网格无关性验证Fig.2 Validation of mesh independency
用砂粒粗糙壁面研究表面粗糙度的影响是研究燃气轮机和其他行业的粗糙度的常见表征方法[3]。Koach和Smith[13]提出实际受污染的压气机中轮廓算数平均偏差Ra和等效砂粒粗糙度ks之间的转换关系ks≈6.2Ra。由于实际表面粗糙元的三维、不规则特性,Rij[14]等人提出了用形状密度因子,来确定ks/k的关系式,通常用可测得的平均峰谷粗糙度Rz代替粗糙元的几何高度k。对于粗糙的砂纸,通常近似为ks=1.5k[13]。
CFX 软件通过在对数速度剖面中引入向下偏移量ΔB,模拟叶栅表面粗糙度对其气动性能的影响差异。
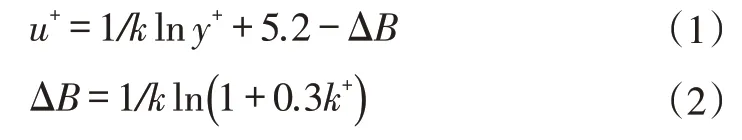
根据粗糙度雷诺数的不同,将粗糙度的影响划分为三个区域:将k+<5定义为水力光滑区,5
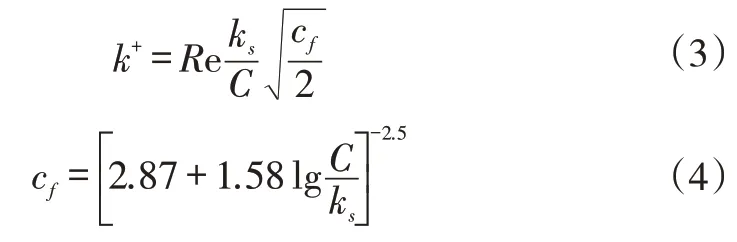
实际叶片表面粗糙度分布是复杂的,为简化研究,本文假设模化叶片与原型叶片具有相同的表面粗糙度分布,并不失一般性,本文认为整个叶片表面粗糙度均匀分布且量级相同,压气机叶片表面ks大致在30~200μm之间,对应k+大致为20~150[16]。
2 粗糙度和雷诺数对叶型损失的影响
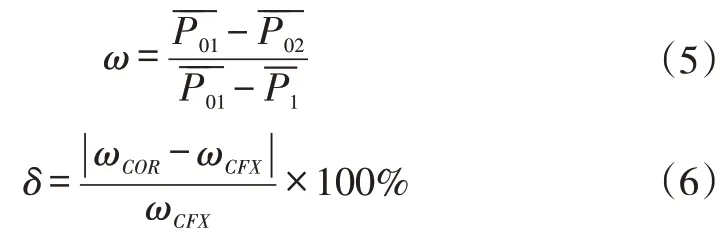
首先分析模化试验叶栅(C=50mm,Re=5.5×105)在ks=30~210μm 条件下的叶型损失特性,按照式(3,4)计算,对应k+在20~150 范围,如图3(a)所示,其中反映三个特征:1)不同表面粗糙度下,叶型损失随来流攻角变化的特性相似。叶栅失速攻角随表面粗糙度增加而增大,这是由于粗糙表面会推迟叶片吸力面可能出现的分离;2)在同一攻角下,随表面粗糙度增加,叶栅损失增大,但当表面达到水力完全粗糙后,增长幅度减缓;3)在叶栅流动达到近失速攻角后,由于叶栅吸力面的分离流动损失逐步成为叶型损失的主要成分,表面粗糙度对叶栅损失的影响程度远低于名义工况和负攻角工况。
其次,类似地我们将叶栅弦长更改为C=30mm 和100mm,对应流动雷诺数分别是3.3×105和1.1×106,采用与图3(a)相同的等效沙粒度,计算各叶栅的损失特性,结果如图3(b)和3(c)所示。对照图3(a),可以明显看到,低雷诺数(3.3×105)的叶栅损失是增加的,而高雷诺数(1.1×106)的损失是下降的,但是同一雷诺数下,粗糙度的影响规律是相似的。
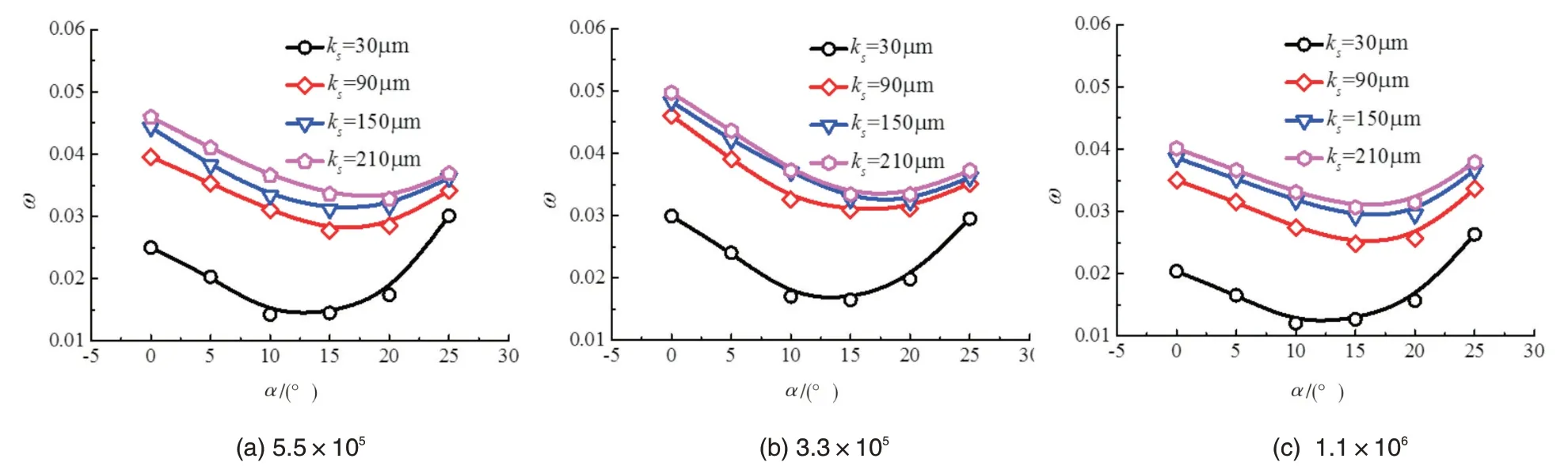
图3 粗糙度对叶型损失系数的影响Fig.3 Effect of roughness on profile loss coefficient
图4 分别对比了当叶片表面粗糙度处于过渡粗糙区(ks=30μm)和水力粗糙区(ks=150μm)时,不同攻角下弦长(Re)对叶型损失的影响。对于同一粗糙度,研究范围内的不同攻角下均呈现出随Re增加叶型损失减小的趋势。

图4 雷诺数对粗糙叶型损失特性的影响Fig.4 Influence of Reynolds number on loss characteristics of rough profile
通过上述分析可见,在不同弦长(Re)下,表面粗糙度的实际影响均可通过k+值的变化体现。在设计攻角12.5°下,缩放前后叶栅叶型损失随k+的变化如图5所示,其中虚线为过渡粗糙区和水力粗糙区的分界线。过渡粗糙区和水力粗糙区随粗糙度的变化,叶型损失呈现出不同的增长趋势。且相较于原型叶栅叶型损失曲线存在一向上或向下的偏移量。在压气机叶栅的模化实验研究中,若测得某一粗糙度下的叶型损失,需分别对粗糙度和雷诺数带来的影响进行修正以得到原型叶栅中任一粗糙度下的叶型损失系数。

图5 设计攻角下缩放前后叶栅叶型损失随K+变化Fig.5 Profile loss varies with K+for original and scaling vane at the design attack angle
综上可以推测:1)表面有一定粗糙度的叶栅缩放后,雷诺数的影响与粗糙度无直接关联,对损失特性的影响类似光滑叶栅的低雷诺数效应,而表面粗糙度的影响规律与雷诺数没有直接关联,但其影响的程度与雷诺数间接有关;2)缩放叶栅气动性能的修正包含了关于雷诺数和表面粗糙度的两个修正,其中表面粗糙度的影响是与流动雷诺数有关的,缩放后性能修正可以分两步完成,从试验叶栅(对应某个Re数和ks值)气动性能,先修正雷诺数的影响,再修正粗糙度的影响,即可得到缩放后叶栅与流动摩阻相关的叶型损失的修正。
3 损失系数修正方法
3.1 粗糙度变化时损失系数修正理论基础
Schlichting[15]研究零压力梯度的管内及平板边界层流动时,可用表面摩擦因子来表征损失系数,对于某个特定粗糙度的壁面,存在两个临界雷诺数,将损失随雷诺数的变化划分为三类流动区域。下临界雷诺数是流动层流或是湍流的判别标准,当流动雷诺数高于下临界雷诺数时,流动位于湍流过渡区,此时若粗糙元略高于粘性底层,则流动损失同时受到表面粗糙度和雷诺数的综合影响。随着雷诺数增大,超过上临界雷诺数时,粗糙元完全穿破边界层层流底层,此时流动损失将只与表面粗糙度有关。基于此理论,研究中认为与零压力梯度的流动类似,压气机效率随雷诺数和表面粗糙度的变化如图6所示。
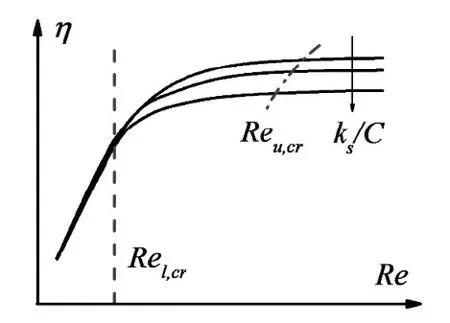
图6 压气机效率随雷诺数及表面粗糙度变化规律Fig.6 Regularity of compressor efficiency with Reynolds number and surface roughness
Syverud[11]、Casey[12]等在研究压气机表面粗糙度对性能的影响中,提出虽流体流过压气机的损失系数比零压力梯度流动大很多,但其中与雷诺数相关的损失可认为与零压力梯度流动中表面摩擦因子随雷诺数和粗糙度的变化类似。在某一参考条件下,可写为如下形式:

考虑到在设计点运行时,不会出现流道两侧附面层合并而充分发展的流动。因此用平板摩擦系数方程比管内充分发展湍流方程计算摩擦因子更为准确,本文中用摩擦因子f代替式(7)中λ,计算方法如下[17]:

3.2 雷诺数变化时损失系数修正理论基础
Schaffler[9]在表面粗糙度和雷诺数对多级轴流压气机影响的研究中提出,对于水力光滑的压气机表面,其多变效率和雷诺数的变化呈如下关系。

其中,n取值范围为0.05~0.2。由此,可得到雷诺数改变时对损失的修正形式:
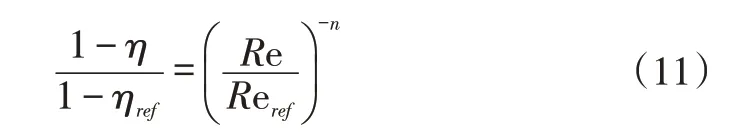
由上述理论,本文将压气机叶栅模化过程中雷诺数和表面粗糙度相对参考工况改变时,关于叶型损失的修正方法记作如下形式:
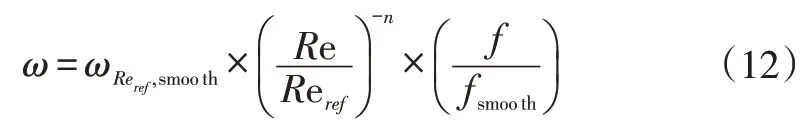
即任一弦长任意粗糙度下的损失系数,可由表面光滑的模化后叶栅叶型损失系数先对雷诺数进行修正,再对表面粗糙度修正得到。本文中n取0.1。
以C=50mm 叶栅为模化后叶栅,实验可测得某一粗糙度下的叶型损失系数,以该工况为参考工况。本文对应Re=5.5×105,ks=120μm为参考工况。此时根据式12 可列出式(13)-(14)。其中下标C表示任意弦长(Re),ks表示任意粗糙度,50 表示C=50mm,ks1表示参考工况下的粗糙度ks=120μm,smooth 代表光滑表面。

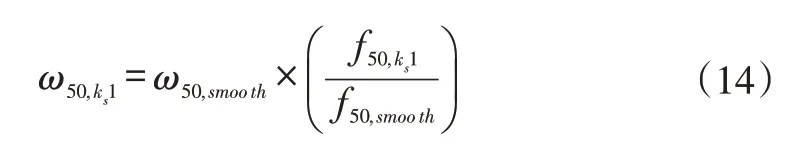
对比式13、14即可得到已知模化后叶栅某一参考工况,对雷诺数和表面粗糙度进行修正后任意弦长和粗糙度下叶型损失的表达式:
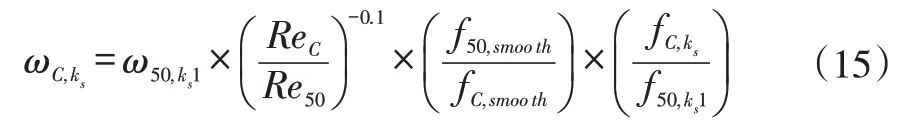
4 叶型损失修正结果分析与讨论
先以模化后叶栅为例,验证修正方法的适用性,如图7所示。在水力粗糙区两者吻合较好,误差在5%以内。但随着粗糙度的减小,达到过渡粗糙时ωCOR与ωCFX间误差增大,修正方法已不能表征叶型损失随粗糙度的变化。这是由于逆压梯度流动中边界层分离现象较为明显,而一定的表面粗糙度会减弱分离,分离损失减小对叶型性能带来积极影响。随表面粗糙度增大分离完全消失,且粗糙元的扰动作用会使得边界层转捩提前,湍流区损失增大。虽本文研究的粗糙度范围已经超过使得分离泡消失的临界粗糙度,但在小粗糙度下,粗糙度带来的损失增加还未掩盖其消除分离的积极影响,因此在过渡粗糙区叶型损失数值计算值低于修正值。

图7 损失修正模型验证Fig.7 Verification of loss correction model
叶型损失变化与平板表面摩擦因子变化呈比例的修正方法适用于水力粗糙区,需对过渡粗糙区叶型损失单独修正。由图7 看出,可用线性关系表征过渡粗糙区叶型损失随粗糙度雷诺数的变化,且由图5 可知随弦长(Re)的变化存在一向上或向下的偏移量,因此需在此基础上考虑对雷诺数的修正。由式15可计算出模化后叶栅k+=70 时的叶型损失,过渡粗糙区以ks=30μm为参考工况,据此可确定k+<70时叶型损失随粗糙度雷诺数的变化关系。
对于本文研究粗糙度范围,C=50mm 的模化后叶栅过渡粗糙区叶型损失系数随k+变化如式16所示。其中,下标ks2表示过渡粗糙区的参考工况,本文中取ks=30μm。再对由于弦长改变导致的雷诺数变化带来的损失进行修正。在式16 的基础上乘以(Re/Re50)-0.1得到与模化后叶栅k+相同时原型叶栅的叶型损失。
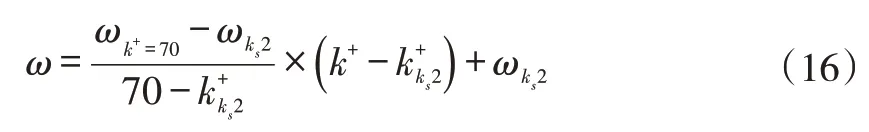
根据上述修正关系对过渡粗糙区和水力粗糙区分别修正,得到模化后叶型及原始叶型的叶型损失ωCOR,与数值模拟计算得到叶型损失ωCFX对比如图8所示,误差δ<15%。
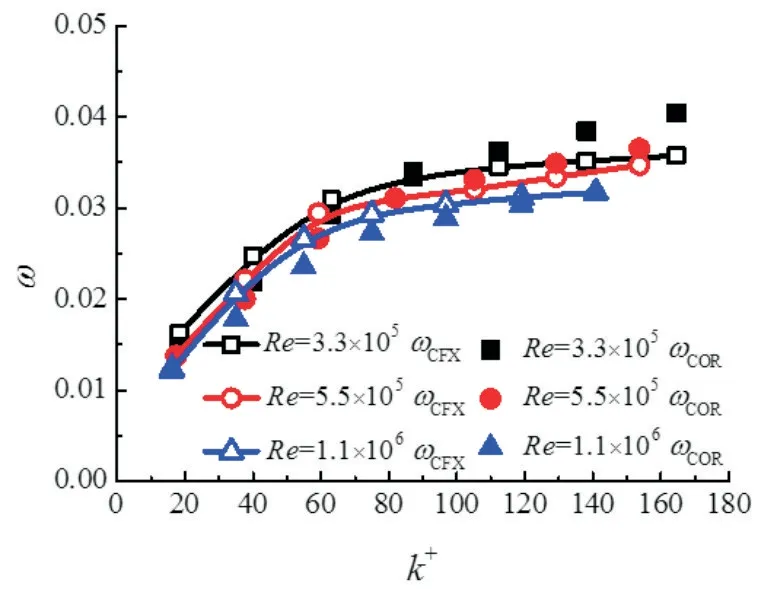
图8 设计攻角下叶型损失修正值与数值结果对比Fig.8 Comparison of experimental and correlation values of profile loss at design attack angle
在运行过程中,受上游流体的影响,流经叶片的气流可能偏离设计进气角,因此需考虑攻角特性。对于几何相似的叶型在相同的气流角下具有类似的流动特征,上述修正方法虽然是在设计攻角下提出的,但在改变攻角后由该修正关系式得到的叶型损失仍能较好的反映雷诺数和粗糙度改变对叶型性能的影响,图9分别为α=5°和α=20°时叶型损失修正值与数值模拟值的对比,除个别点外,整体误差在15%以内。
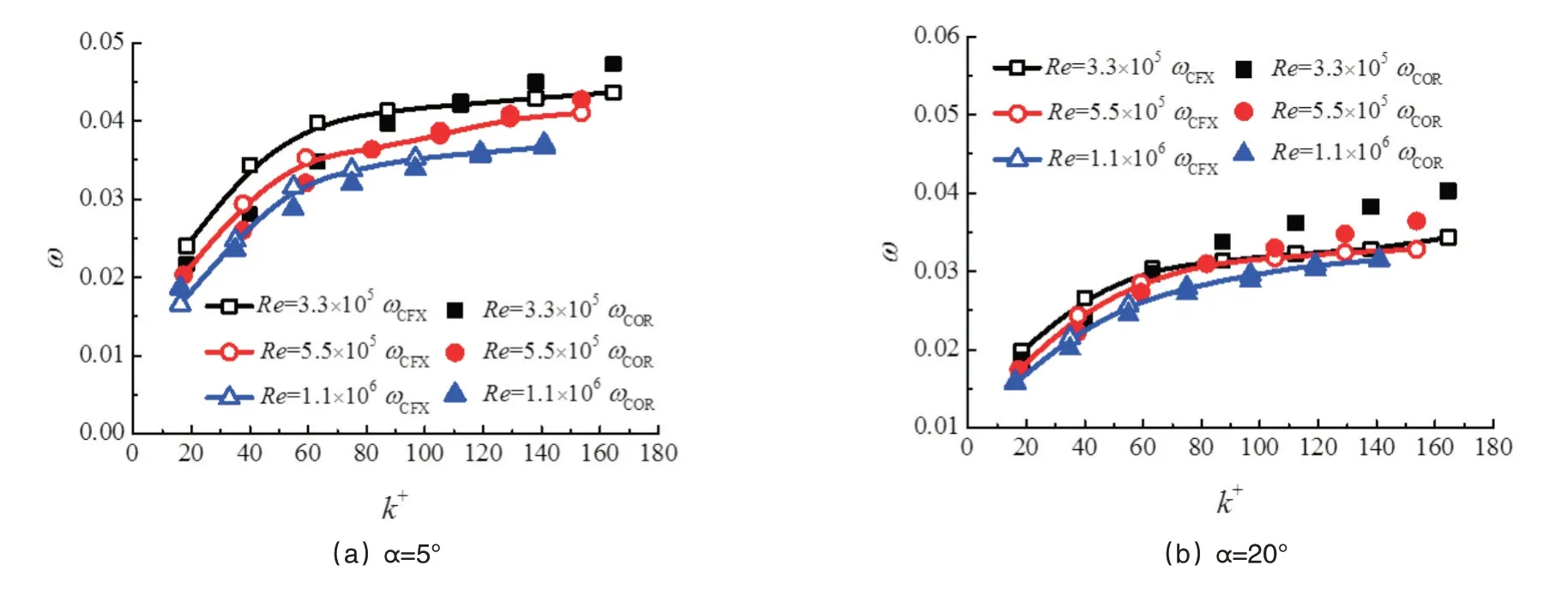
图9 非设计攻角叶型损失修正值与数值结果对比Fig.9 Comparison of experimental and correlation values of profile loss at off-design attack angle
5 结论
本文以NACA65 叶型为研究对象,基于表面粗糙度对平板边界层流动的影响规律及雷诺数对水力光滑压气机性能的影响规律,建立了一套针对实验缩放问题中叶型性能的换算方法,主要结论如下:
1)对于模化前后的压气机叶栅,不同攻角下叶型损失随粗糙度的变化规律类似,处于过渡粗糙区时叶型损失随粗糙度的增加急剧增大,而水力粗糙区叶型损失随粗糙度的变化增长减缓。在同一表面粗糙度下,叶型损失随弦长(Re)的增大而减小。
2)水力粗糙区,叶型损失相对参考工况的变化与平板表面摩擦因子随雷诺数和表面粗糙度的变化有较好的一致性;而过渡粗糙区,由临界粗糙度雷诺数对应叶型损失与参考工况确定的ω随k+变化的线性关系对叶型损失修正效果更佳。
3)不同攻角下,修正关系式计算得到的叶型损失均可大致反映模化过程中雷诺数和表面粗糙度改变对性能影响的总体趋势,与数值计算结果误差在15%以内。
