Optimization Design of Centrifugal Pump Impeller Based on Intelligent Optimization Algorithm
2022-01-11WeiweiWangLeiGuo
Wei-wei Wang Lei Guo
(Hi-key Tech Co.,Ltd.)
Abstract:The research object of this paper is a centrifugal pump with a specific speed of 67.The optimization objectives are efficiency and NPSHr of the pump.The 15 main design variables include impeller inlet diameter ds,impeller outlet diameter d2,impeller outlet width b2,shroud and hub profile,axial height of impeller Deta Z,balde outlet angle Beta2,number of blades,wrap angle,etc.The professional rotating machine software CFturbo have been used to creat the parameterized model of a centrifugal pump.Using advanced intelligent optimization algorithm to perform multi-objective optimization of objective function.The optimal combination of 15 design variables is obtained.Then,The model of centrifugal pump before and after optimization was numerically calculated by professional rotating machinery analysis software Simerics MP+.The results showed that the hydraulic efficiency and NPSHr of the optimized pump model were improved.
Keywords:Centrifugal Pump;Multi-objective Optimization;Intelligent Optimization Algorithm;Hydraulic Efficiency;NPSHr;Numerical Simulation
Nomenclature
ηhydraulic efficiency,%
NPSHr net positive suction head required,m
dsimpeller inlet diameter,m
d2impeller outlet diameter,m
b2impeller outlet width,m
Deta Z axial height of impeller,m
Beta2 blade outlet angle,degree
Theta wrap angle,degree
ggravitational acceleration,m/s2
ρdensity,kg/m3
ηvhydraulic efficiency
vu1circumferential component of the absolute velocity at the impeller inlet,m/s
u1circumferential speed at the impeller inlet,m/s
Qrated volume flow,m3/s
Hrated head,m
Prated power,W
V1average velocity of impeller inlet,m/s
W1relative velocity of impeller inlet,m/s
λ1coefficient of pressure drop due to absolute velocity change and hydraulic loss,the value is 1.2
λdrag coefficient of impeller inlet,the value generally is 0.4 without impact inflow
nsspecific speed
0 Introduction
As an important part of the centrifugal pump,the hydraulic design quality of the impeller often determines its performance.The common centrifugal pump impeller design methods are mainly classified into forward design and inverse design.The inverse design is difficult to process due to the complex shape of the blades,so it is less applied to actual engineering.The forward design conducts simulation analysis on a given product and make repeated corrections to the geometric model according to the analysis results until the better hydraulic performance impeller is obtained.However,this process takes a long time and heavy repetitive work,which results in a long product development cycle.
In order to solve the above problems,more and more engineers apply the optimization ideas to the research and development of impellers.Yuan et al.(2014)[1]used the orthogonal design method to optimize the design of automobile cooling water pump.The results verified the feasibility of orthogonal design and obtained the influence of impeller parameters on the performance of cooling water pump.Xiao and Wang(2006)[2]used combinatorial optimization strategy to optimize the design of the centrifugal pump impeller and achieved good results.However,at present,most optimization designs are single-objective with certain limitations.
This paper takes centrifugal pump impeller as the research object,and takes hydraulic efficiency and NPSHr as optimization objectives.Confirming the weight of objectives with the super-transitive approximate method,the multi-objective optimization problem is transformed into a single-objective optimization problem.The excellent intelligent optimization algorithm is combined to find the optimal solution within the range of each design parameter.
1 Parameterization of Impeller Model
1.1 Parameterization of Meridian Plane
Fig.1 shows the shape of the blade meridian.In this paper,the parameterization of meridional plane is realized by using Bezier curve.The shroud and hub profiles are controlled by Bezier curves with 5 control points,respectively.As long as the coordinates of the control points P2,P3,P4,P7,P8,and P9 are modified,the shape of the meridional plane can be changed.In order to reduce the number of independent variables,P3 and P8 are selected as variables.The position of the blade inlet edge on the shroud and hub is adjusted by modifying points P11 and P12.Axial length of impeller is controlled by Deta Z.
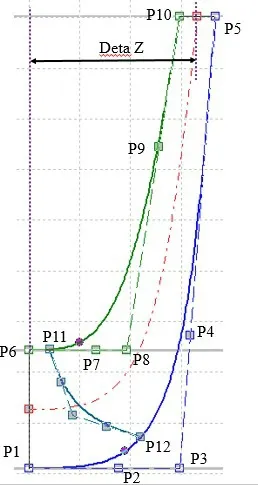
Fig.1 Schematic Diagram of Parameterization of Meridian Plane
1.2 Parameterization of 3D Blade Shape
The 3D blade shape is mainly controlled by parameters such as the inlet angle,outlet angle,wrap angle and blade thickness.Based on 5 stream surfaces(including shroud and hub),this paper calculates the inlet and outlet ongles of the blades on each stream surface.Blade wrap angle is abtained by point-by-point integration method.The change law of blade wrap angle and blade thickness is obtained by calculation,the profile of each flow surface is obtained by integrating them,and finally the 3D blade shape is generated.
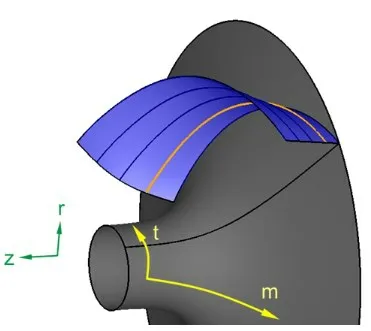
Fig.2 Schematic diagram of parameterization of 3D blade shape
2 Numerical Simulation
With model determined,it needs to be numerically simulated to obtain the hydraulic performance.Because of performance comparison between optimization models is the focus here,and no precise computation is required,the mesh and solution accuracy can be reduced appropriately.As long as all models use the same mesh resolution,the comparison results of different models have reference value.In order to shorten the simulation time,the k-e model is used to calculate the flow field in the whole flow passage of the centrifugal pump under steady state.
3 Optimization Objective
The relationship between optimization objectives and independent variables is established by the excellent intelligent optimization algorithm.Then the optimal solutions within the range of variables are obtained by continuously performing random combinations between independent variables.
3.1 Hydraulic Efficiency Objective
The hydraulic efficiency of a centrifugal pump is defined as follows,

According to the above formula,on the premise that the head meets the design conditions,increasing the hydraulic efficiencyηis to reduce the powerP.This gives the following objective function,

3.2 NPSHr Objective
NPSHr of a centrifugal pump is defined as follows,


Single-stage single-suction centrifugal pump inlets are usually straight conical,namely without inlet preswirl,which gives,

According to formula(3),NPSHr actually represents the lowest pressure drop at the pump inlet.If this value is small,the energy loss from the pump inlet to the lowest pressure position is the smallest,which means that the cavitation resistance of the pump is better.Thus,the other objective function is,

3.3 Determination of Optimization Objective Weights
For multi-objective optimization,the weight of each optimization objective is different.This paper hopes that the importance of efficiency in optimization is higher than the cavitation resistance of pump.The weight coefficients of the centrifugal pump efficiency and NPSHr are determined by the super-transitive approximate method.Then we will systematically explain how the super-transfer approximation method reasonably stipulates the weight coefficient of the optimization target.
1)Generate a binary comparison matrixA
It is difficult to directly define the specific weightωmof themgoal in general,but it is easier to compare the weights between the two targets.Assuming that there arenoptimization target values in total,n(n-1)/2 comparisons will be made between the weight coefficients of the two targets.Now suppose the comparison value of thei-thtarget to thejthtarget isaij,whenaijis greater than 1,it means that the importance of thei-thtarget is greater than thej-th;Whenaijis less than 1,it means that the importance of thej-thtarget is greater than thei-th;whenaij=1,it mean that the two goals are equally important.Therefore,a binary comparison matrix A can be generated,and any elementaij≠1/aijin matrixA.
2)Construct complementary matrixA(n)
Constructing complementary matrixA(1),A(2),…A(n),where complementary matrixA(i)=(a1(i),a2(i),…,an(i))T,the ith row elementai(i)of the complementary matrixA(i)has the same importance as thei-throwaiof the matrixA,the other row elements of the complementary matrix are shown by the following formula:

3)Construct super-transitive approximationA*

Hereaij(1),aij(2),...,aij(n)represent the elements of matrixA(1),A(2),...,A(n)in thei-throw andj-thcolumn respectively.
4)Eigenvector method to obtain weight coefficient
Find the eigenvectors of the super-transfer approximate matrixA*,The eigenvector component corresponding to the maximum eigenvalue is the weight coefficient of the corresponding target,as shown in equation(13);
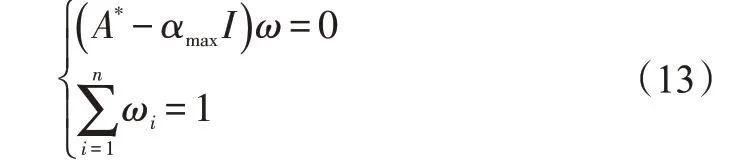
In the formula,ωis the eigenvector corresponding to the maximum eigenvalue αmaxofA*,and its componentωi(i=1,2,...,n)is the weight coefficient of the corresponding objective function.In this paper,there are 2 optimization goals,that is,n=2.The importance of the efficiency in this paper is about twice the cavitation resistance of the pump.The weight coefficients corresponding to each optimization goal finally obtained according to the above steps are shown in equation(14):

In the formula,ω1andω2respectively represent the weighting coefficient of the efficiency of the centrifugal pump and of the anti-cavitation allowance.Therefore,the final optimization objective equation is,

4 Intelligent Optimization Method
In this paper,an intelligent optimization method based on machine learning was chosen for multi-objective optimization of centrifugal pump,and the optimization algorithm includes Mode Pursuing Sampling(MPS),Pareto Set Pursing(PSP)and Radial Basis Function based High Dimensional Model Representation(RBF-HDMR).It is particularly good at solving some large variables,strong constraints and black box problems.Moreover,the optimization algorithm is automatically matched according to the optimization objectives,optimization variables and constraints,without the need for artificial selection.
5 Results and Discussions
The low specific speed centrifugal pump is selected for this optimization case,and the specific parameters are shown in Tab.1.

Tab.1 Rated parameters of centrifugal pump
With the optimization variables determined,the value range of each optimization variable must be considered reasonably.If the value range is too large,the optimization time will be increased.If the value range is too small,the optimal solution may be missed.Considering the geometric parameters of the initial model,the value range of each variable are determined as shown below.
0.055m≤ds≤0.1m
0.17m≤d2≤0.25m
0.005m≤b2≤0.015m
0.03m≤DetaZ≤0.035m
0.03m≤P3_X_hub≤0.04m
0.015m ≤P3_X_shroud≤0.02m
0.03m ≤P8_Y_shroud≤0.035m
20%≤LE position at hub≤40%
5%≤TE position at shroud≤15%
18°≤Beta2 ≤30°
90°≤Theta≤180°l
4 ≤Number of baldes≤9
In order to ensure the validity of the optimization results,the centrifugal pump head as the constraint condition.That is,the optimized result head is at least 46.41m.
Tab.2 shows the results of the performance of the centrifugal pump before and after optimization.Fig.3 and 4 show the shape of meridian plane and the 3D blade shape before and after optimization,respectively.That means that the hydraulic efficiency and cavitation performance of the centrifugal pump is proved obviously after optimized.

Tab.2 Rated parameters of centrifugal pump

Fig.3 Comparison of meridian plane before and after optimization

Fig.4 Comparison of the 3D blade shape before and after optimization
For the purpose of obtaining the performance of the centrifugal pump before and after optimization in more detail,three monitoring points are set in the volute,which monitor pressure fluctuation at different locations.Fig.5 shows the positions of the three monitoring points,and Fig.s 6 to 8 show the comparison results of the pressure fluctuation at monitoring points P1 to P3,respectively.The blue curve in the figure is the pressure fluctuation before optimization,and the red curve is the pressure fluctuation after optimization.
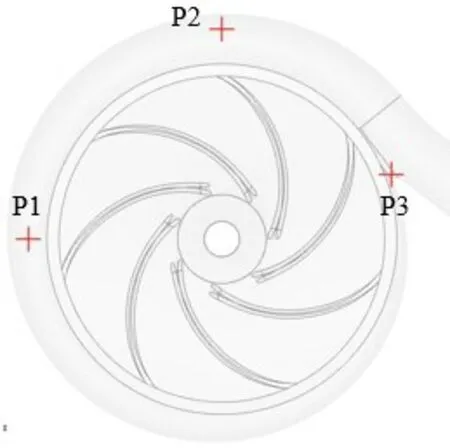
Fig.5 Distribution of monitoring points in the volute
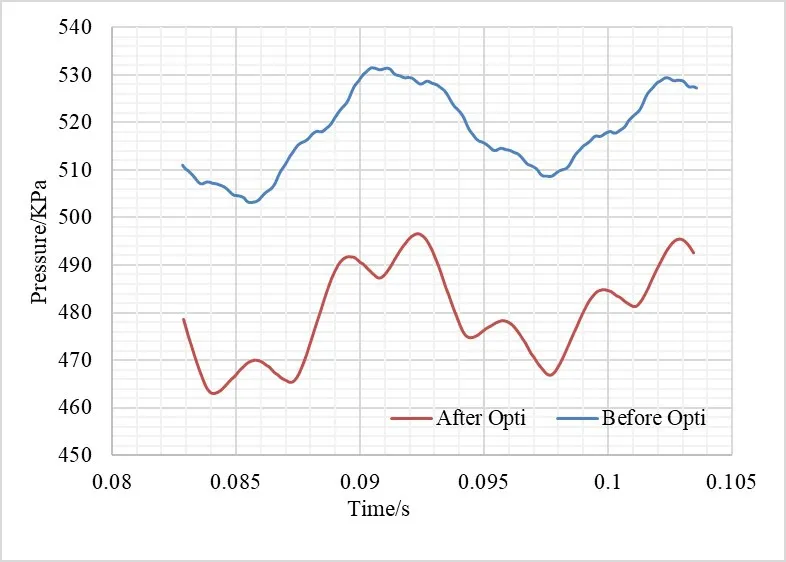
Fig.6 Pressure distribution of monitoring point P1

Fig.7 Pressure distribution of monitoring point P2
According to the pressure distribution before optimization in Fig.6~ Fig.8,The pressure fluctuation at point P3 near the tongue in Fig.8 is more severe and the pressure amplitude is larger compared with the other two points.It means that the pressure fluctuation near the tongue is more significant than other areas because of the strong coupling interference between the impeller and the volute.The pressure curve of point P2 fluctuates more strongly than that of point P1,because point P2 is closer to point P3,so it is more susceptible to the influence of the wake caused by the blade sweeping the septum tongue.

Fig.8 Pressure distribution of monitoring point P3
Comparing the pressure curves of different positions of the volute before and after optimization,it can be seen that:the pressure fluctuations of after optimized are more stable and the fluctuation amplitudes decreases,which means that the stability of the pump has been improved overall.
Fig.9 shows the distribution of total gas volume fraction before and after optimization.As can be seen from the figure,the gas volume fraction of leading eage after optimization is much lower than before optimization,which means that the cavitation performance of leading blade is improved obviously.This shows that the optimal design is successful.

Fig.9 Distribution of total gas volume fraction
6 Conclusion
This paper proposes a multi-objective optimization analysis method using CFD technology,which is used to realize parametric design of centrifugal pump flow components by integrating CFD pre-processing,solution and post-processing.Analysis shows,compared with the model before optimization,the hydraulic efficiency at the design point is increased by 4.24%,NPSHr is reduced by 1.49m,and the pressure fluctuation at different positions of the volute is significantly decreased after optimization.It shows that the optimization design is useful and can be generalized to the optimization design of other rotating machinery products.
