基于改进QMAP的贝叶斯网络参数学习算法

邸若海, 李叶, 万开方, 吕志刚, 王鹏

(1.西安工业大学 电子信息工程学院, 陕西 西安 710021; 2.西北工业大学 电子信息学院, 陕西 西安 710072)

针对小数据集条件下的贝叶斯网络参数学习问题，目前主要通过引入参数约束来优化参数学习过程。根据约束数量的不同，现有的研究分为单一约束和多种约束2种情况。

针对单一约束，Writting等[1]利用定性影响约束构造惩罚函数，并将最大熵函数与惩罚函数结合构造目标优化函数，最后利用改进的APN算法对参数进行求解；Feelders等[2-3]将定性影响条件下的参数学习看作一个保序回归问题，首先采用最大似然估计算法得到参数初始值，然后结合定性影响约束和保序回归法估计参数。Plajner等[4]分别利用梯度下降法、保序回归来处理单调性约束，大幅度提高了参数学习的精度。国内学者周鋆等[5]通过引入平滑先验来优化似然函数，并将定性影响约束作为一个惩罚项与改进后的似然函数构成参数目标优化函数，采用梯度下降方法进行求解。邸若海等[6-7]通过构造单调性约束表示专家经验，然后将单调性约束转化为狄利克雷分布的超参数，进而结合最大后验概率估计获取贝叶斯网络参数。任佳等[8]采用区间约束限制参数学习，将区间约束转化为贝塔分布的超参数，进而结合贝叶斯估计学习参数。黄政等[9]将近似相等的先验约束以正态分布的形式融入到单调性约束的贝叶斯参数学习过程中，提高了参数学习的精度。

由于单一约束方法一般只针对某种特殊的专家知识，限制了专家经验的利用，学习精度一般。因此，利用多种约束进行参数学习受到了更多的关注。Niculescu等[10]和Campos等[11]提出基于凸优化的参数学习方法。Liao等[12]结合EM算法，将约束引入到数据缺失条件下的BN参数学习。Zhou等[13-14]提出约束多项式分布参数学习(multinomial parameter learning with constraints,MPL-C)方法。郭志高等[15]提出基于双重约束的参数学习方法。Rui等[16]提出基于定性最大后验概率(qualitative maximum a posterior,QMAP)的参数学习方法，采用拒绝-接受采样的方法获取满足约束的模型参数，并利用采样所得参数的均值替代先验参数的分布，进而利用MAP计算对应的模型参数的后验估计。与其他算法相比，QMAP算法不仅给出了一个在多约束条件下的贝叶斯网络参数学习通用框架，而且具有较好的学习效果。在此基础上，Guo等[17]利用QMAP算法学习参数，并进一步利用参数约束判断参数的合理性，避免了QMAP算法所得参数不满足约束的情况。然而，当网络复杂度变大，参数约束较多或约束可行域较小时，由于拒绝-接受采用算法本身的随机性，导致难以获得满足约束的参数。从而导致QMAP算法非常耗时。

针对上述问题，本文设计了一种新的约束区域中心点的解析计算方法来替代原有的拒绝-采样方法，在此基础上，提出了CMAP(constrained maximum a posteriori)算法。首先，设计一种新的目标函数，结合参数约束构建一个带约束的目标优化问题；其次，利用一种寻优引擎来求解该目标优化问题获得约束区域的边界点和中心点，最终以获得的中心点作为待求参数的先验分布，并利用MAP求取待求参数的后验估计。

1 贝叶斯网络

下面给出贝叶斯网络一般的定义：

定义1贝叶斯网络[18]由结构G和参数Θ两部分组成。贝叶斯网络的结构为一个有向无环图G=(V,E),其中节点变量集合V={X1,X2,…,Xn}表示变量,有向边集合E描述变量间的依赖关系。贝叶斯网络的参数Θ={θi}i=1,2,…,n为一组条件概率分布,每个节点存储其自身与其父节点集之间的条件概率分布,即P(Xi|Pa(Xi))。

即贝叶斯网络包含定性和定量两部分内容。在定性层面,有向无环图描述变量之间的依赖或独立关系。在定量层面,条件概率分布表示变量之间依赖程度的大小。

贝叶斯网络通过引入条件独立性完成了联合概率分布的分解,它将联合概率分布P分解为

(1)

式中,Xi可取离散值和连续值。

2 参数的先验分布及约束类型

2.1 参数先验分布

贝叶斯公式将先验分布和似然函数结合,得到θ后验分布即

P(θ|D)∝P(θ)L(θ|D)

(2)

式中,概率分布P(θ)表示θ的先验知识,似然函数L(θ|D)=P(D|θ)表示数据集D的影响。在i.i.d条件下,(2)式中L(θ|D)为多项式似然函数的共轭分布,假设先验分布P(θ)是Dirichlet分布,即

(3)

则后验分布P(θ|D)也是Dirichlet分布。在观测样本下,θ的后验分布P(θ|D)为

(4)

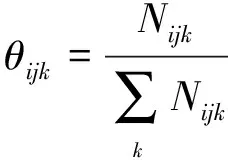
(5)

Dirichlet先验分布中参数的物理意义不明显,领域专家难以直接确定,在实际应用中存在困难。根据Dirichlet分布特性,其条件分布和边缘分布都是Beta分布且Beta分布为二项式分布的共轭分布族,因此可以通过确定Beta分布中的2个形参来近似表达与其相关的领域知识。

根据贝叶斯估计和领域知识建立的先验Beta分布模型,在i.i.d条件下(6)式成立

P(θ)=B[α1,α2]θα1-1(1-θ)α2-1

(6)

(7)

2.2 参数约束类型

基于小数据集的参数学习,仅依靠数据已经不能获取满足精度要求的参数。因此,现在的方法都是将先验知识引入到参数学习过程之中,来弥补数据的不足。先验知识一般通过不同形式的参数约束来表示,主要的参数约束如表1所示。

表1 参数约束类型

3 基于改进QMAP的贝叶斯网络参数学习算法

3.1 低维参数约束域的可视化及中心点计算

首先分析参数约束区域的特点,分别给出二维和三维情况下约束区域中心点的计算方法。在二维状态下,假设参数满足以下约束

(8)

通过将约束区域可视化,图1中加粗的线条区域就是参数的约束域,即线段AC。只需获取A点和C点的坐标,即可获得线段AC的中点。本文将求取点A和C坐标的问题转化为一个带约束的优化问题,通过公式(9)可以求取点C的坐标,通过公式(10)可以求取A点的坐标。

min[(θ1-0)2+(θ2-1)2]

(9)

min[(θ1-1)2+(θ2-0)2]

(10)

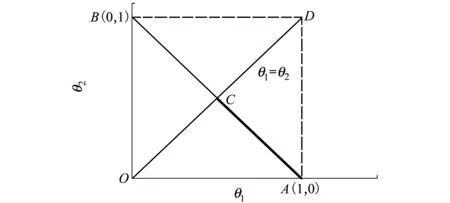
图1 二维参数的可行域

在三维情况下,假设参数满足以下约束

(11)

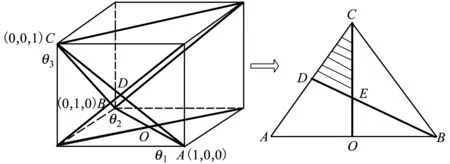
图2 三维参数的可行域

从图2可以看出,参数的约束区域为△CDE,类似于二维的情况,将其转化为一个目标最优化问题,具体如下

下面给出本文参数约束域中心点计算的一般化的方法,设待求参数

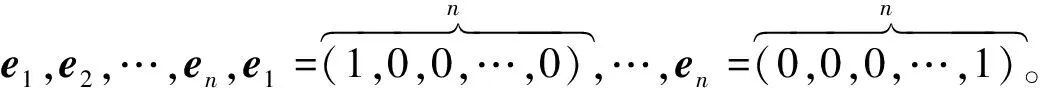
(15)

当参数不包含分布间约束时,可根据参数的局部独立性,将上述高维(mq)的优化问题化简为低维(m)的优化问题。具体如下所示：

(16)

式中,w=1,2,…,q,总共需要求解mq个m维的优化问题。

通过(15)～(16)式可以求取约束区域的边界点,本文通过边界点直接求平均的方式求取约束区域的中心点,在二维情况下肯定能够获取中心点。在三维情况下,当约束区域为三角形时,可以获得约束区域的中心点,当约束区域为四边形时,只能获取近似的中心点。在高维情况下,也会存在只能获取近似中心点的情况。这是本文算法精度稍差于QMAP算法的原因。

3.2 CMAP算法

CMAP算法的具体步骤如下:

步骤1 记录样本数据中的节点状态统计量Nij和Nijk。

步骤2 利用优化引擎求解(15)～(16)式,以求取参数约束的边界点,进而对边界点进行平均,获取参数约束的中心点。利用中心点替代待求参数的先验分布,进而代入最大后验估计公式(17)获取待求参数的后验估计。

(17)

式中：Mijk=A*P(Xi=k|Πi=j,Ω),A为等价样本量。P(Xi=k|Πi=j,Ω)为待求参数的先验分布,这里用中心点的坐标替代。这是本文算法与QMAP算法最大的不同。QMAP算法是用得到满足约束的参数均值替代参数的先验分布。

步骤3 利用交叉验证方法确定系数A即等价样本量。

步骤4 根据公式(17)完成定性最大后验概率估计。

3.3 算例说明

为了更好地解释本文的算法,接下来通过一个简单的算例来说明。

图3 一个简单的贝叶斯网络

假设图3中节点B的参数是待求的参数,此时,已知的参数约束为

(18)

θ1,θ2,θ3,θ4组成了4维参数空间,首先判断参数的约束类型是否包含第2节中的分布间约束,如果不包含,则可以利用参数的局部独立性将待求参数进行分解和降维。如果包含,则无法利用参数的局部独立性将参数进行分解和降维。很明显,公式(18)中包含分布间约束θ1>θ3,无法利用参数局部独立性。针对这种情况,本文利用标准单位基向量构建目标函数

(θ3-0)2+(θ4-0)2]

(19)

(θ3-0)2+(θ4-0)2]

(20)

(θ3-1)2+(θ4-0)2]

(21)

(θ3-0)2+(θ4-1)2]

(22)

公式(19)～(22)给出了利用标准基向量构建目标优化函数的方法。利用公式(19)～(22)可以求得参数约束域的4个边界点,进而将这4个点的坐标进行平均,用平均所得的点来近似替代参数约束域的中心点。

假设参数约束中不包含分布间约束,便可利用参数的局部独立性将其分解。具体如下所示：

由(23)～(26)式可知,当参数约束中不存在分布间约束时,可以将原来4维的参数约束空间分解为2个2维的参数约束空间,降低待求问题的复杂度。

4 仿真结果及分析

为了验证本文算法的有效性,分别利用Asia、Alarm、Win95PTs和Andes网络进行仿真验证。这些网络经常被用于贝叶斯网络的结构和参数学习算法验证,表2给出了这几个网络的基本信息。采用平均KL距离来衡量参数学习的精度,公式(27)给出了KL距离的计算公式,其中P(X)表示求出的样本分布,Q(X)表示真实的样本分布。采用平均运行时间来衡量算法的效率。本文中的运行时间是通过Matlab中的Tic-Toc指令获取。算法运行20次,求均值和方差。

(27)

表2 仿真网络信息

4.1 仿真实验1

本节考虑参数的分布间约束,部分仿真结果如表3所示。

表3 不同算法的KL距离比较

表4 不同算法的运行时间比较

图4 不同算法的平均运行时间比较(Alarm网络)

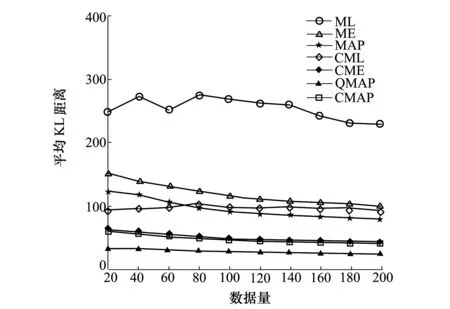
图5 不同算法的平均KL距离比较(Alarm网络)

通过对表3～4和图4～5中的实验结果进行分析,可以得到以下结论:

1) 所有算法的学习精度排序为QMAP>CMAP>others。

2) 所有算法运行时间的大致排序为QMAP>CME>CMAP>others。

3) 本文提出的CMAP的学习精度稍差于QMAP算法,但运行效率高于QMAP算法。

4.2 仿真实验2

本节不考虑参数的分布间约束,则可通过公式(16)对公式(15)进行降维,通过对表5～6和图6～7中的实验结果进行分析,可以得到以下结论:

1) 所有算法的学习精度排序为QMAP>CMAP>others。

所有算法的运行时间的大致排序为QMAP>CME>CMAP>others

表5 不同算法的KL距离比较

图6 不同算法的平均KL距离比较(Alarm网络)

图7 不同算法的平均运行时间比较(Alarm网络)

表6 不同算法的运行时间比较

5 结 论

为了提高QMAP算法的学习效率同时又不影响其学习精度，本文设计了一种新的约束区域中心点的解析计算方法来替代原有的拒绝-接受采样计算方法。仿真实验证明，本文提出的CMAP算法的参数学习精度稍差于QMAP算法，但计算效率比QMAP算法高出一个量级。缺点是CMAP算法仍涉及最优化问题求解的引擎，引擎的优劣直接决定了算法的时效性，下一步研究工作是引入更高效的引擎用于求解参数约束域的中心点，进一步提高本文提出的参数学习方法的效率。