基于粒子群极值Kriging模型的压气机叶盘时变可靠性分析

2022-01-11王远卓韩治国杨子煜路成薛小锋

西北工业大学学报 2021年6期

王远卓, 韩治国, 杨子煜, 路成, 薛小锋

1.北京航空航天大学宇航学院, 北京100191; 2.西北工业大学航天学院, 陕西西安710072;3.复旦大学航空航天系, 上海200433; 4.西北工业大学航空学院, 陕西西安710072

低压压气机转子系统对于航空发动机的正常运转起到尤为重要的作用，其功用是通过压缩气体来提升整个系统的热力循环效率。低压压气机叶盘工作环境严苛，承受着高压、高转速等交变载荷作用[1]，一旦发生功能失常，将对航空发动机产生二次损伤，造成灾难性后果。因此，为了保障航空发动机系统安全运行，有必要开展低压压气机叶盘时变可靠性分析。

近年来，国内外学者基于蒙特卡洛(Monte Carlo,MC)模拟与近似解析法开展了许多研究，对航空发动机压气机叶盘进行了可靠性分析。赵洪利等[2]基于MC模拟，给出了用于评估航空发动机发生故障可能性的风险预测方法；Narayanan等[3]提出了基于MC模拟的航空发动机结构疲劳寿命估算方法；杨周等[4]根据模拟的随机参数与随机响应的关系，通过一次二阶矩法对发动机进行可靠性分析；张飞[5]对一次二阶矩法在均值点进行线性化展开的基础上进行改进，提出了通过在验算点进行线性化对发动机叶盘进行可靠性分析的改进一次二阶矩方法；白冰等[6]针对强非线性问题高精度可靠性求解困难的问题，依据二次二阶矩建立了可靠度指标分析方法。上述研究工作为航空发动机压气机叶盘结构可靠性分析提供了思路，但MC模拟需要通过大规模计算来实现可靠性分析，耗时较长且不能高效完成具有动态时变特性的可靠性评估；近似解析法适用于功能函数已知的可靠性分析，对于压气机叶盘这类复杂结构可靠性分析，其功能函数通常是未知的。为合理规避MC模拟与近似解析法存在的缺点，许多专家学者通过构建代理模型进行结构可靠性分析。高阳等[7]提出了径向基函数神经网络模型，对高压涡轮盘疲劳可靠性分析进行了研究；刘佳奇等[8]基于智能神经网络提出了一种航空发动机运行状态下的时变安全性分析方法；马小骏等[9]基于最小二乘支持向量机算法对航空发动机寿命进行了分析。上述代理模型虽然一定程度上提高了可靠性分析的效率，但是对于具有时变特性的可靠性分析问题，需要建立大量的代理模型获取结构可靠性指标，其分析流程过于复杂。因此，部分学者将极值思想引入代理模型来简化可靠性计算的负担。Zhang等[10-11]为有效地进行涡轮叶盘疲劳可靠性及中心齿轮可靠性分析，基于响应面方法，借鉴极值思想提出了多重极值响应面策略； Bai等[12]针对航空发动机叶盘的非确定性因素提出了一种基于动态子结构的极值响应面法。然而，上述方法在构建功能函数过程中采用的是基于二次多项式的形式，其可靠性分析精度与工程需求存在偏差。

为了解决上述问题，本文基于Kriging模型，结合极值思想和粒子群算法(PSO)，提出了粒子群极值Kriging模型方法(PSOEKM)，用以实现航空发动机低压压气机叶盘时变可靠性分析。其中，极值思想用以简化动态分析流程，以输出响应的极值代替整个时变过程；PSO算法用以替代梯度下降，实现Kriging模型超参数寻优；Kriging模型用于建立输出响应与输入参数之间关系，进而实现可靠性分析。此外，通过多种方法对比验证了本文研究方法的有效性与可行性。

1 粒子群极值Kriging模型

1.1 分析流程

为了合理高效实现航空发动机低压压气机叶盘时变可靠性分析，将极值思想和PSO算法引入Kriging模型，提出PSOEKM方法，其原理为：结合极值思想处理压气机叶盘输出响应的时变过程，运用输出响应极值将动态分析转化为瞬态分析；采用PSO算法实现目标函数求解，获取Kriging模型的超参数；利用Kriging模型描述输出响应与输入参数之间的关系，构建功能函数并实现时变可靠性分析。基于PSOEKM方法的航空发动机低压压气机叶盘时变可靠性分析流程如图1所示。

图1 基于PSOEKM方法的航空发动机低压压气机叶盘时变可靠性分析流程

由图1可知，基于PSOEKM方法的压气机叶盘动态时变可靠性分析包括确定性分析、样本获取、模型构建、时变可靠性分析4个部分。具体分析流程如下：

1) 构建航空发动机低压压气机叶盘三维有限元模型，设置材料参数、边界条件与动态载荷；执行动态确定性分析；获取输出响应随时间变化的规律并结合极值思想确定输出响应极值与研究时刻点。

2) 基于输入变量随机分布特征，获取足够的输入样本，通过确定性分析计算各输入样本对应的输出响应值；确定用以建模的训练样本和用以模型验证的测试样本。

3) 结合训练样本，运用PSO算法实现模型超参数寻优，并求解PSOEKM的模型系数，构建压气机叶盘输出响应与输入参数之间的关系模型。其中，基于PSO算法的模型超参数求解步骤为：参数初始化，适应度函数值计算，更新粒子的位置与速度、个体极值与群体极值，完成迭代获取模型超参数。

4) 在建立的压气机叶盘输出响应模型基础上，构建其极限状态函数，采用MC方法进行大量模拟实现压气机叶盘时变可靠性分析并输出结果。

1.2 数学模型

参考Kriging模型,PSOEKM模型y(x)可描述为[13]

y(x)=GT(x)α+z(x)

(1)

式中:y(x)为输出响应值;α为待定系数向量;z(x)为误差修正函数;G(x)为基函数矩阵。

与传统的响应面法相比,Kriging模型的优势主要体现在误差修正项z(x),该项的引入可进一步提升了模型变量之间的关联程度,进而提升了代理模型的精度。通常,误差修正函数z(x)服从均值为0、方差为σ2的正态分布[14],即

(2)

式中:E为函数均值;var为函数方差;cov为函数的协方差;R为相关函数矩阵,p,q=1, 2, …,m;m为训练样本的数量;xp,xq为第p和q个训练样本。

xp与xq的相关函数为

(3)

式中:i=1, 2, …,n,n为训练样本的维度;θi为第i个模型的超参数。

相关函数常用的形式有指数型、高斯型及线性型等,本文选取高斯型函数作为相关函数的形式,原因在于该形式函数具有较好的拟合性能[15],高斯型相关函数(3)式可表达为

(4)

因此,基于样本的相关函数矩阵R为

(5)

进而,模型中的待定系数向量α可由(6)式确定

α=(GT(x)R-1G(x))-1GT(x)R-1Ytrain

(6)

式中,Ytrain为训练样本的输出向量。

则误差修正函数为

z(x)=rT(x)R-1(Y-GTα)

(7)

式中,rT(x)表示单个样本与所有样本相关性大小。

rT=[(R(θ,x,x1)R(θ,x,x2…R(θ,x,xm)]。

依据最小二乘理论,模型误差的方差估计值为

(8)

模型超参数传统上采用梯度下降法,通过最大化适应度函数进行求解获取。然而,对于涉及多变量参数高非线性问题,梯度下降策略寻优效率下降,甚至无法得到全局最优解。因此,本文将最大化问题转化为最小化问题[16]

(9)

式中,f(θ)为适应度函数。

为了实现最小化问题求解,采用粒子群算法通过求解(9)式实现模型超参数θ的寻优。粒子群算法通过粒子的随机性、记忆性、不确定性,改善了基于梯度下降模型参数寻优容易陷入局部最优的问题。相比遗传算法,PSO算法在更新过程中实时追踪当前最优粒子,故收敛速度较快[17],可以较好、较快地满足时变条件下的可靠性分析。粒子群算法粒子的速度和位置更新如(10)式所示

(10)

式中:k为迭代次数;v(k)为当前粒子速度;x(k)为当前粒子位置;c1和c2为学习因子;β为随机产生的随机数;xpbest为个体最优值;xgbest为全局最优值。

基于上述分析,结合训练样本运用粒子群算法可实现模型超参数寻优,进而结合最小二乘法实现模型系数求解,建立PSOEKM模型(功能函数)。

1.3 时变可靠性分析

基于所构建的功能函数,结合分析目标的许用值,可建立发动机压气机叶盘径向变形的极限状态函数,其可表达为[18]

(11)

在此基础上,运用MC法对极限状态函数进行大量抽样,利用概率统计分析实现时变可靠性分析,其原理实质是借鉴伯努利大数定律,即

(12)

式中:nB为n次试验下事件B出现的次数;P为事件B出现的概率;ε为任意很小的正数。

根据(12)式,当试验次数n趋近于无限大时,n次试验中满足可靠性阈值要求的次数将收敛到实际的可靠度,则可靠度计算原理为

(13)

式中:R(t)为可靠度函数;pr(t)为可靠密度函数;r(t)为0～t时间段内累积的故障数;N0为t=0时规定条件下进行工作的产品数。

2 算例分析

2.1 动态确定性分析

压气机工作环境复杂,叶盘作为压气机重要的部件之一,其可靠性直接关乎航空发动机整个系统的安全性。选取某型航空发动机低压压气机叶盘作为研究对象,考虑流体载荷和结构载荷的作用,对其径向变形进行动态可靠性分析。为了实现低压压气机叶盘径向变形动态可靠性分析,首先建立研究对象的三维模型(如图2所示),结合构建的三维模型,进而生成低压压气机叶盘的有限元模型(如图3所示),航空发动机低压压气机叶盘由四面体单元组成,包括150 837个节点和89 424个单元。

图2 低压压气机叶盘三维模型

图3 低压压气机叶盘有限元模型

选取1Cr11Ni2W2MoV作为低压压气机叶盘材料,其密度为7.8×103kg/m3、泊松比为0.3、弹性模量为2.06×1011Pa。此外,考虑进口流速、出口压力、密度和转速等作用,其中进口流速为124 m/s,出口压力为5.07×105Pa,以及转速为1 168 rad/s。需要说明的是:转速是随时间变化的,其变化特性参考文献[16]确定。在有限元模型和载荷参数设置的基础上,结合有限元法和有限元体积法对压气机叶盘径向变形进行动态确定性分析。在动态确定性分析过程中,分别针对流场和结构场进行设置:在流场中设置进口流速和出口压力载荷;在结构场中,设置材料参数、转速。最后对低压压气机叶盘设置圆柱支撑约束。基于确定性分析得到低压压气机叶盘径向变形随时间变化曲线如图4所示。

图4 低压压气机叶盘径向变形随时间的变化曲线

由图4可知,低压压气机叶盘径向变形的最大值出现在分析时域[165 s, 200 s],任意选取其中某一时刻作为研究时刻点,本文选取t=172 s,则此时的径向变形分布云图如图5所示。由图5可以看出,低压压气机叶盘径向变形的最大位置位于叶尖尖端,同时将该部位作为时变可靠性分析研究的部位。

图5 低压压气机叶盘径向变形分布云图

2.2 样本获取

基于低压压气机叶盘径向变形动态确定性分析,结合其最大值出现的时刻和位置,选取进口流速v、出口压力pout、密度ρ和转速w作为随机输入变量,假设这些变量参数均服从正态分布且相互独立,其数值分布特征如表1所示[19-20]。

依据表1输入变量的随机分布特征,运用拉丁超立方抽样获取随机输入变量的样本,并结合多次动态确定性分析计算输入样本对应的输出响应极值(最大径向变形),进而形成含有输入变量和输出响应的样本。其中,随机选取一部分样本作为训练样本,用以构建低压压气机叶盘径向变形的PSOEKM模型(功能函数);剩余的样本用以验证PSOEKM模型的精度。

表1 输入变量的随机分布特征

2.3 模型构建

基于动态确定性分析获取的训练样本,结合1.2节数学模型构建原理,运用粒子群算法实现PSOEKM模型超参数寻优。其中,粒子群算法寻优的初始化条件设置参数为:学习因子c1=0.56,c2=1.95、最大迭代次数为25、种群规模为20、进化速度范围为[-13,13]、进化位置范围为[0.1,20]。基于粒子群算法的适应度函数进化曲线如图6所示。

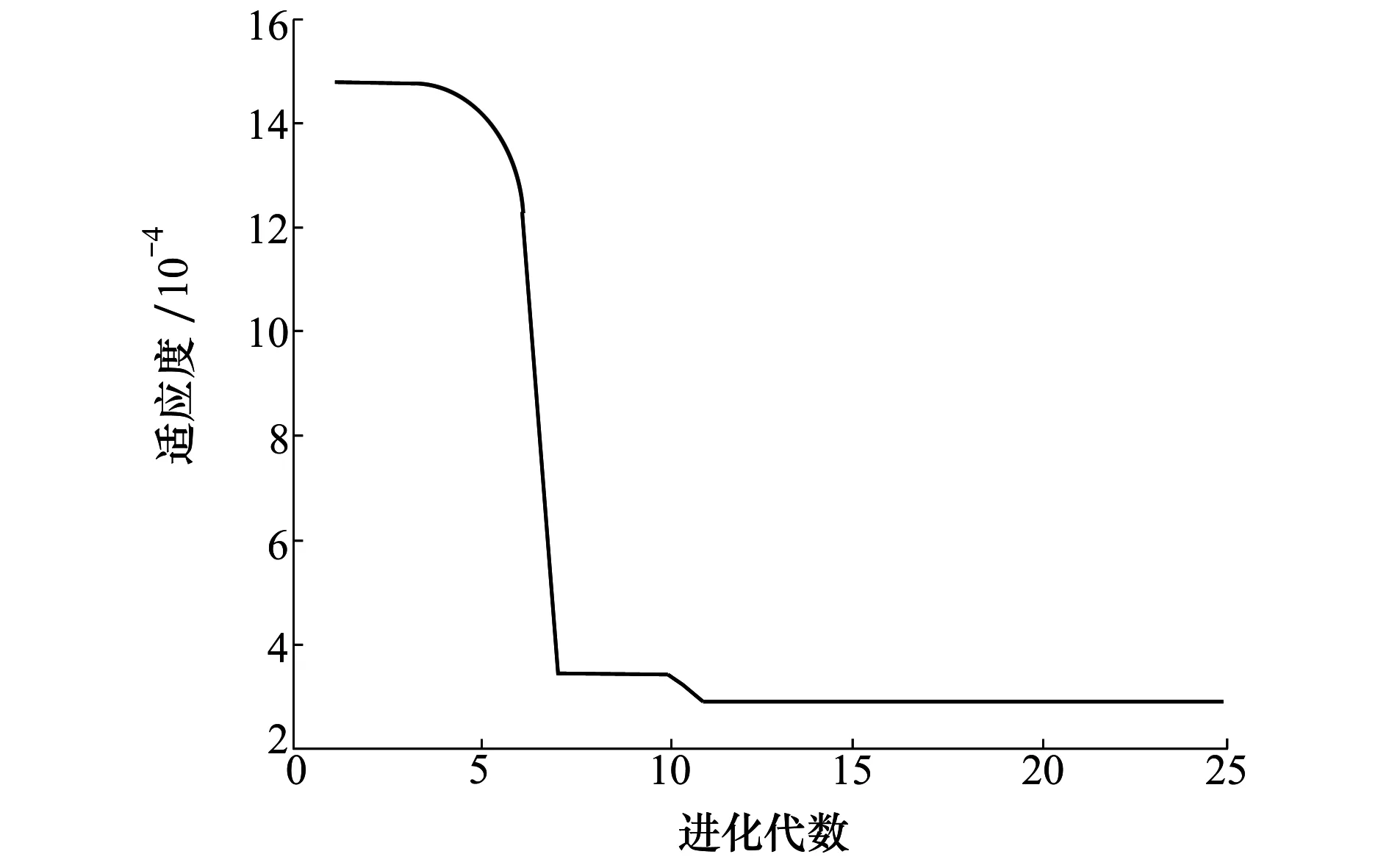
图6 基于粒子群算法的适应度函数进化曲线

从图6可以看出,整个粒子适应度函数收敛的过程中,开始收敛速度较快,随着迭代次数的增加,收敛速度变慢直至稳定。群体粒子适应度通过7次迭代基本收敛,在第12次迭代时目标值达到最小,稳态值为2.9×10-4。此时,PSOEKM模型超参数θ=[0.716,13.500,0.521,0.223]。

在得到模型超参数的基础上,为构建低压压气机叶盘径向变形的功能函数,采用最小二乘法实现PSOEKM模型相关函数矩阵R与待定系数α向量的求解

(14)

2.4 可靠性分析

基于建立的功能函数,结合低压压气机叶盘径向变形的许用值,其极限状态函数根据(11)式可表达为

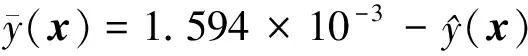
(15)

利用MC法对(15)式进行10 000次仿真抽样,则低压压气机叶盘径向变形的仿真历史与分布直方图分别如图7～8所示。由图7和图8可知,低压压气机叶盘径向变形服从正态分布。当低压压气机叶盘径向变形许用值为1.594×10-3m(该值基于3σ原则确定)时[16],可靠度为99.76%,满足工程需求。

图7 低压压气机叶盘径向变形仿真历史

图8 低压压气机叶盘径向变形分布直方图

3 粒子群极值Kriging模型验证

3.1 建模特性

为了说明PSOEKM在建模特性方面的优势,基于测试样本,通过均方根误差ERMS和平均相对误差Ear对其建模精度进行研究,其计算原理见(16)式。在PSOEKM建模特性过程中,通过极值响应面法(extremum response surface method,ERSM)和极值Kriging模型(extremum Kriging model,EKM)进行对比分析。需要说明的是:所有的计算在相同的计算环境下执行;ERSM和EKM模型均是采用相同的训练样本构建;在建模精度分析过程中,以低压压气机叶盘径向变形动态确定性分析结果作为参考;在建模效率方面,则是以ERSM建模时间作为参考。建模精度与效率分析结果如表2所示。

(16)

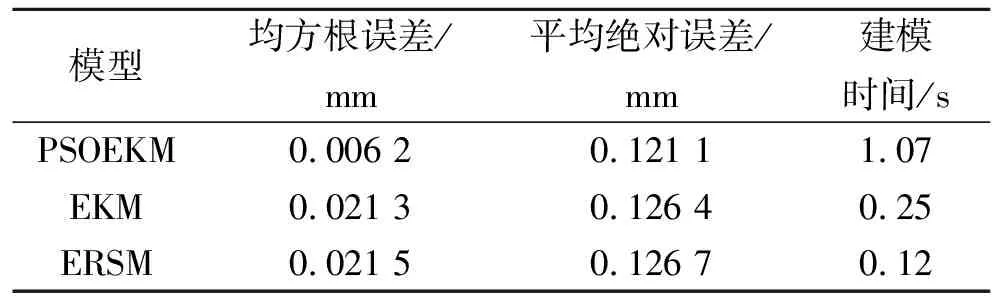
表2 建模精度与效率分析结果

由表2可以看出,PSOEKM的建模时间相对于EKM和ERSM略有增长,其原因是PSO在模型超参数寻优过程中存在多次迭代计算,但是其建模效率是可接受的。在建模精度方面,相较于EKM和ERSM,所提出的PSOEKM具有一定的优势,PSOEKM的均方根误差和平均绝对误差小于ERSM和EKM的均方根误差和平均绝对误差,并且PSOEKM的建模精度相对于ERSM和EKM分别提高了4.62%和4.38%。因此,在建模效率可接受范围内,PSOEKM在建模精度方面具有明显的优势。

3.2 仿真性能

PSOEKM方法的仿真性能主要从仿真效率和分析精度两方面进行研究,结合多种方法对比分析的手段加以说明,其中所用的方法有直接模拟法、ERSM和EKM。基于表1中输入变量数值随机的分布特征,分别将4种方法用于执行不同频次(102,103和104)的MC抽样,实现低压压气机叶盘径向变形时变可靠性分析。其中,由于计算限制没有执行104次直接模拟。此外,在仿真性能分析过程中,以直接模拟的分析结果作为参考。基于ERSM、EKM和PSOEKM的仿真性能分析结果如表3～5所示。

表3 仿真效率分析结果 s

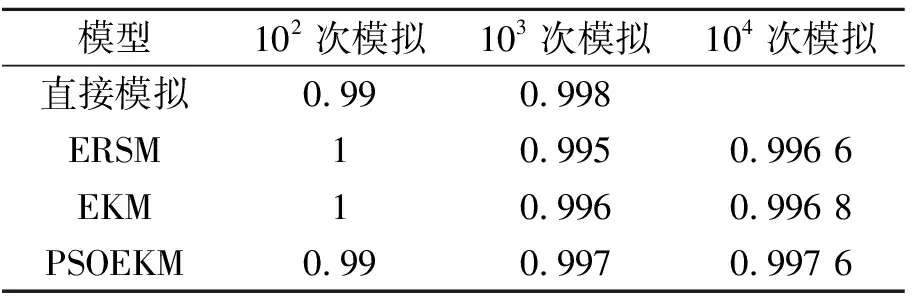
表4 仿真可靠性分析结果

表5 仿真精度分析结果 %

由表3可知,代理模型(包括PSOEKM、EKM和ERSM)的仿真时间远远小于直接模拟的仿真时间,由表4～5可以看出,在不同的仿真模拟次数下,PSOEKM的仿真结果优于ERSM和EKM的仿真结果,并且其分析结果与直接模拟的结果最为接近;相较于ERSM和EKM,PSOEKM的仿真精度分别提升了0.61%和0.11%。因此,PSOEKM在仿真特性方面具有一定的优势。