机器人踩踏式除草过程仿真分析与试验研究
2022-01-10庞业忠
张 勤,庞业忠,王 凯
(华南理工大学机械与汽车工程学院,广东广州 510641)
随着现代农业的发展,人们的环境保护意识逐渐加强,对食品质量安全问题也愈加重视。无农药或仅用少量农药的有机栽培水稻越来越受青睐,其种植面积逐年扩大,利用机器人除草已成为有机水田杂草去除对策研究的重要课题。踩踏式除草是常用的有机水田除草方式[1-2],其有效性已得到大量田间试验的验证[3-4]。对除草过程进行分析与评价是除草机器人设计的重要环节,由于田间实地除草试验季节性强,成本高及周期长,可通过有限元仿真来分析机器人除草过程,以揭示机器人与水田土层、水层之间的动态耦合关系和评价除草效果。该方法具有周期短、变换灵活等优势,其在机器人运动分析、结构优化和性能评价方面得到了广泛应用。针对机器人除草过程分析及除草效果评价,国内外学者做了大量研究。
在除草过程分析方面,Azimi-Nejadian等[5]结合FEM(finite element method,有限元法)和回归分析法建立了犁板-土壤相互作用的仿真模型,分析了犁板作业参数和土壤性质对耕作力的影响;Zhang等[6]基于欧拉-拉格朗日耦合法建立了切削刃-土壤相互作用的仿真模型,探讨了仿真分析方法的可行性以及计算了仿真结果与试验结果的相对误差;Wei等[7]基于流体动力学方法建立了犁刀-土壤相互作用的仿真模型,分析了耕作速度、耕作深度对犁刀载荷和磨损率的影响;Ucgul等[8]基于DEM(discrete element method,离散单元法)建立了切削刃-土壤相互作用的仿真模型,分析了切削刃几何形状对耕作力和土壤变形情况的影响;齐龙等[9-10]基于ANSYS/LS-DYNA软件中的ALE(arbitrary Lagrange-Euler,任意拉格朗日-欧拉)算法建立了除草轮-水-土壤相互作用的仿真模型,分析了除草轮几何参数对切削阻力和土壤破坏能力的影响。
在除草效果评价方面,通常采用田间试验或仿真分析方法。Teruaki等[1-2]、Sori等[3]和 Fukushima等[4]通过多年跟踪对比薄膜覆盖除草、机器人踩踏式除草和不进行除草处理的实验,分析了机器人踩踏次数、踩踏轨迹对除草效果的影响;王金峰等[11]、陈学深等[12]和Tao等[13]通过统计除草作业前后杂草的数量变化和秧苗的受损情况,选取了最优的除草机器人结构参数和作业参数,该方法结果直观及准确率高,但成本高且局限性大;黄小龙等[14]基于运动轨迹分析软件建立了苗间锄草机器人锄草刀的运动学模型,并以覆盖率和入侵率(代替除草率和伤苗率)为评价指标,分析了锄草刀几何参数和作业参数对苗间除草效果的影响;齐龙等[15]基于ANSYS/LS-DYNA软件中的ALE算法,以耦合应力和土壤扰动率为评价指标,研究了耙压式除草轮转速和水田环境因素对除草效果的影响;张明举等[16]基于ADAMS(automatic dynamic analysis of mechanical systems,机械系统动力学自动分析)软件建立了八爪式机械除草装置的运动学模型,以铲齿运动轨迹单次覆盖的苗间间隙面积和重复覆盖面积为评价指标,分析了铲齿几何参数和运动参数对除草效果的影响。
综合国内外研究现状可以看出,现有的除草过程仿真分析方法主要关注除草设备与土壤单相流的相互作用过程,很少考虑水层对土壤运动状态的影响以及它们之间的多相耦合关系;提出的除草效果评价指标主要适用于铲除式行间除草方式。基于此,笔者以踩踏式除草机器人为研究对象,基于ANSYS/LS-DYNA软件中的SPH(smoothed particle hydrodynamics,平滑粒子流体动力学)算法建立机器人踩踏式除草过程的多相流耦合模型,分析踩踏式除草过程中水田土层与水层之间的动态变化关系;提出一种踩踏式除草效果的综合评价方法;通过仿真和田间试验来分析机器人踩踏式除草过程,以讨论机器人质量、运动速度和水层厚度对除草效果的影响,并通过对比来验证仿真分析结果的可靠性。
1 机器人踩踏式除草过程分析与评价
1.1 踩踏式除草机器人的结构与除草机理
踩踏式除草方式适用于生长初期的杂草,除草作业一般开始于插秧7 d后,持续7周左右[2]。踩踏式除草机器人的结构如图1(a)所示,包括摄像组件、箱体和踩踏组件三部分。其中,踩踏组件由2组履带式移动机构(包含履带、驱动轮、踩踏轮、张紧轮和连接部件)组成,其通过丝杠连接,分跨在箱体的两侧,分别由2个电机单独驱动,实现机器人的移动和踩踏功能;箱体内集成了图像处理模块和运动控制模块,其与摄像组件共同作用,实现机器人的运动控制功能[17-19]。

图1 踩踏式除草机器人结构示意Fig.1 Structure diagram of pedaling weeding robot
踩踏式除草机器人通过在水田秧苗行间的简单行走来踩踏杂草,实现杂草的切断、拔出;同时,机器人行走时产生的浑浊泥水可抑制杂草的光合作用,且被搅起的土壤沉积后覆盖于秧苗株间的杂草上,破坏了杂草的生长环境,达到了去除行间和株间杂草的目的。
1.2 除草效果影响因素分析
由上述除草机理可知,踩踏式除草机器人对水田土层和水层的踩踏作用、冲击能力是影响除草效果的主要因素,其中踩踏效果主要与机器人的结构参数、运动参数以及水田环境因素有关。机器人的结构参数主要包括履带的前、后倾角θ1和θ2,履带接地长度L,链轮半径R以及机器人质量M。其中,履带的前、后倾角θ1和θ2直接影响机器人对水田土层和水层的推动、挤压和搅拌作用,并可能会引发对水田的二次破坏,对除草效果的影响较大。考虑到机器人的正、反双向运动,取θ1=θ2,为保证机器人的运动平稳性以及结合履带与驱动轮和踩踏轮的包络角,取θ1=θ2=50°;履带接地长度L主要决定了机器人对水田土层支撑面的压力,为避免机器人的下陷量过大,选取形状较优的矩形履带[20],并取L=0.52 m;为保证较好的踩踏效果以及合适的踩踏轮包络角,取R=0.11 m。由于机器人的踩踏速度较慢,运动参数主要考虑平均运动速度v,其主要影响机器人对流变性水田土壤的破坏程度[21]。水田环境因素主要包括土壤种类、水层厚度hw等,当作业地域确定时,土壤种类和机器人下陷量hs随之确定。而水层厚度hw一方面对土壤的变形起缓冲和黏滞作用,另一方面影响水层的浑浊程度,在满足农艺种植要求的前提下,可通过适当调节水层厚度hw来获取更好的除草效果。为了简化模型且又不失一般性,本文主要研究机器人质量M、运动速度v和水层厚度hw对踩踏式除草效果的影响。
1.3 除草效果评价指标确定
踩踏式除草机器人对水田秧苗行间杂草的踩踏能力取决于踩踏运动对土层的破坏程度,可用土壤扰动率来描述;机器人行走过程中对水田土层、水层的冲击能力表现为踩踏后水层浑浊程度的变化,可用水层密度增量来描述。基于此,本文以土壤扰动率和水层密度增量为机器人踩踏式除草效果的评价指标。
机器人踩踏前后水田土层的变形情况如图2所示。图中:S0为踩踏前水田土层的初始面积;S1为踩踏后的压痕面积;S2为踩踏后水田土层的剩余面积。

图2 机器人踩踏前后水田土层的变形示意Fig.2 Deformation diagram of paddy field soil layer before and after robot pedaling
基于图2,土壤扰动率δ1可表示为:
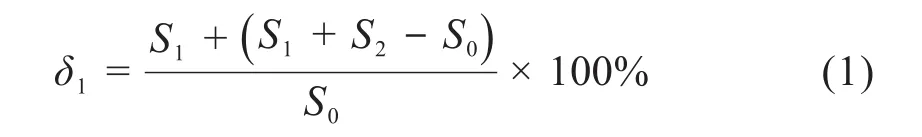
通过测量机器人踩踏前后水田土层的面积和压痕面积,求得土壤扰动率δ1。δ1越大说明机器人对水田土层的挤压、破坏程度越大,对杂草的碾压强度越大,即除草效果越好。
水层密度增量δ2可表示为:
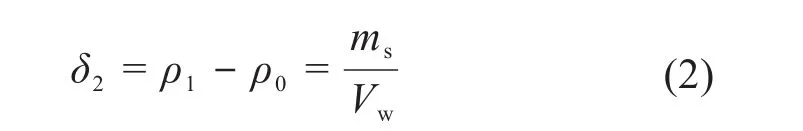
式中:ρ0、ρ1分别为踩踏前后水层的密度;ms为踩踏后溶入水层的土壤颗粒质量;Vw为作业区域的水层体积。
通过统计踩踏后溶入水层的土壤颗粒质量ms与水层体积Vw,求得水层密度增量δ2。δ2越大说明水中溶入的土壤颗粒越多,水层浊度越大,即抑制杂草光合作用的效果越好。
为了综合评价除草效果,对土壤扰动率δ1和水层密度增量δ2进行归一化处理,并结合加权因子和映射函数构建综合评价函数φx,φx越大说明综合除草效果越好。
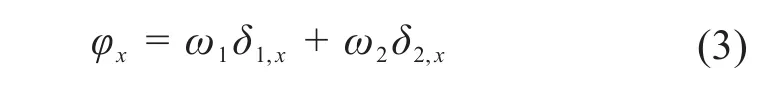
其中:

式中:δk,x为第x次试验对应的评价指标δk的值;δk,min、δk,max分别为评价指标δk的最小值和最大值;ω1、ω2为加权因子,其取值由水田土层的松软程度决定,土层越松软说明越容易形成淤泥层,导致机器人对其的挤压、破坏作用减弱,则土壤颗粒越容易溶入水层,即土层越松软,ω1取值越小,ω2取值越大。
2 机器人踩踏式除草过程的有限元模型建立
踩踏式除草过程是机器人踩踏组件与水田土层、水层相互作用的动态过程。为模拟该除草过程,采用ANSYS软件进行仿真分析。分析过程分为前处理和后处理:前处理由ANSYS/LS-DYNA软件完成,包括有限元模型的建立、约束与载荷的施加以及关键字文件的生成,其中有限元模型的构建包括踩踏式除草机器人有限元模型、水土耦合模型的建立以及流固耦合关系的定义;后处理由LS-PrePos软件完成,包括结果分析和数据提取。基于上述步骤,动态模拟机器人在水田中的踩踏式除草过程,并根据仿真结果综合评价除草效果。
2.1 踩踏式除草机器人有限元模型建立
因ANSYS/LS-DYNA软件在建模方面存在不足,本文先采用SolidWorks软件构建踩踏式除草机器人的三维模型,再将该模型导入ANSYS/LS-DYNA软件进行仿真分析。在除草过程中,机器人与水田土层、水层相互作用,考虑到ANSYS/LS-DYNA软件的计算能力有限,且机器人踩踏组件直接作用于土壤,为节省计算时间和便于网格划分,在此做简化处理,即重点分析机器人踩踏组件与水田土层、水层之间的相互作用。鉴于机器人踩踏组件的刚度远高于水田土层的刚度,则机器人模型选用刚性体模型。为了便于与后续试验结果比较,根据机器人样机设定相关参数:履带的材料为PVC(polyvinyl chloride,聚氯乙烯),密度为1 380 kg/m3,弹性模量为3.5×109MPa,泊松比为0.319;踩踏轮和箱体的材料为铝合金,密度为2 810 kg/m3,弹性模量为 7.17×1010MPa,泊松比为0.33。由于履带和踩踏轮为主要接触零部件,采用六面体网格进行划分,以提高计算精度;箱体为次要接触零部件且形状不规则,采用四面体网格进行划分,以节省计算时间;采用对称化建模方式,只构建单侧踩踏组件的模型。构建的踩踏式除草机器人有限元模型如图3所示。

图3 踩踏式除草机器人有限元模型Fig.3 Finite element model of pedaling weeding robot
2.2 水土耦合模型建立
水田包括土层和水层,以ANSYS/LS-DYNA软件中的MAT_147(MAT_FHWA_SOLID)为土壤本构模型,该模型扩展了含水率、变形率的影响和补充了单元删除算法,并结合Drucker-Prager准则对传统Mohr-Coulomb准则进行了修正,加快了收敛速度[22]。
构建土壤本构模型时,选择我国南方最为典型的粉质黏土,其参数如下:密度为1 758 kg/m3,土粒比重为 2.15,体积模量为 2.583×105Pa,剪切模量为1.192×105Pa,内摩擦角为0.129 rad,黏聚力为7 001 Pa,含水率为46.6%;其余参数按经验值选取[23-24]。
水层模型位于土层模型上方,以ANSYS/LS-DYNA软件中的MAT_9(MAT_NULL)为水介质本构模型,并以*EOS_GRUNEISEN为状态方程。这样一方面可正确构建水、空气等介质的力学模型并反映其形变,另一方面可以评估水介质的失效行为以及热行为。水的主要参数如下:密度为998.21 kg/m3,截止压力为-100 Pa,黏性系数为8.684×10-4Pa⋅s。
2.3 流固耦合关系定义
常用的3种流固耦合模拟方法为FEM、ALE算法和SPH算法。相比其他2种算法,SPH算法在模拟水田土层、水层的大变形运动时具有明显的优势,其以光滑粒子模拟土壤与水的相互作用、混合以及从踩踏组件间隙穿过的现象。因此,本文采用SPH算法对水田土层、水层有限元模型进行重建模和求解,通过*CONTROL_SPH和*SECTION_SPH打开SPH算法。在该算法中,不同物质粒子自动接触,无须额外定义,机器人有限元模型与水土耦合模型约束为自动点面接触。由于水土耦合模型在有限空间内存在边界反作用力,其底部采用全自由度约束,左侧面采用对称约束,其余3个侧面通过*BOUNDARY_SPH_SYMMETRY_PLANE配置虚粒子,以模拟真实情况下水田环境的远场边界。基于上述方法建立的机器人踩踏式除草过程有限元模型如图4所示。
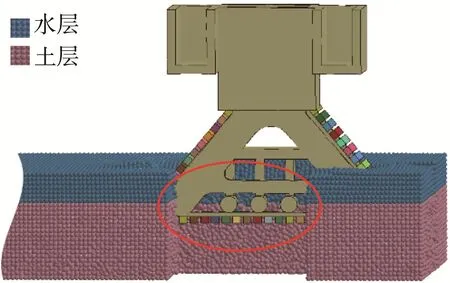
图4 耦合平衡的机器人踩踏式除草过程有限元模型Fig.4 Finite element model of robot pedaling weeding process with coupling balance
3 机器人踩踏式除草过程仿真分析
3.1 有限元模型验证
为验证所构建的机器人踩踏式除草过程有限元模型的可靠性,设踩踏式除草机器人(M=52 kg)在水田中的下陷量hs=0.06 m,运动速度v=0.125 m/s;土层长度lm=2.2 m、宽度bm=0.6 m、厚度hm=0.23 m;水层厚度hw=0.07 m。利用构建的有限元模型对踩踏式除草过程进行仿真分析,结果如图5所示。选取水田与机器人前端的踩踏轮(前轮)相切的A-A截面为参考面,整个除草过程分为3个阶段:挤压剪切阶段(Ⅰ阶段,即①—③)、踩踏阶段(Ⅱ阶段,即④—⑤)和扰动平衡阶段(Ⅲ阶段,即⑥—⑦)。图6所示为机器人踩踏后A-A截面处土层深度随时间的变化情况。
由图5和图6可知,在Ⅰ阶段(t01—t1),踩踏式除草机器人前轮挤压周围的土层和水层,原有的水土耦合平衡被破坏,水回流后填平土层凹坑,并不断冲刷周围的土层,水层的浑浊程度增大。当前轮开始推动挤压A-A截面时,土层向前隆起变形,略有增高;随着除草过程的推进,土层不断被踩踏,土层深度逐渐减小。在Ⅱ阶段(t1—t2),机器人后端的踩踏轮(后轮)与履带跟随前轮踩踏土层,导致土层形成压痕,并对土层和水层造成进一步的扰动和冲击,使水层的浑浊程度进一步增大,在此阶段土层与水层的深度随踩踏扰动震荡变化;在Ⅲ阶段(t2—t3),水回流,水中的土壤逐渐沉淀,形成稳定的土层压痕轮廓,建立了新的水土耦合平衡状态。由此可以看出,机器人踩踏式除草过程实质上是一个准静态过程,经历了水土耦合平衡的建立、破坏、再建立的转换,而平衡转换的瞬间又为动态过程。通过仿真分析可知,基于有限元模型模拟的踩踏式除草过程与实际除草过程非常相似,说明所构建的模型能够较好地描述机器人踩踏式除草过程,验证了模型的可靠性。
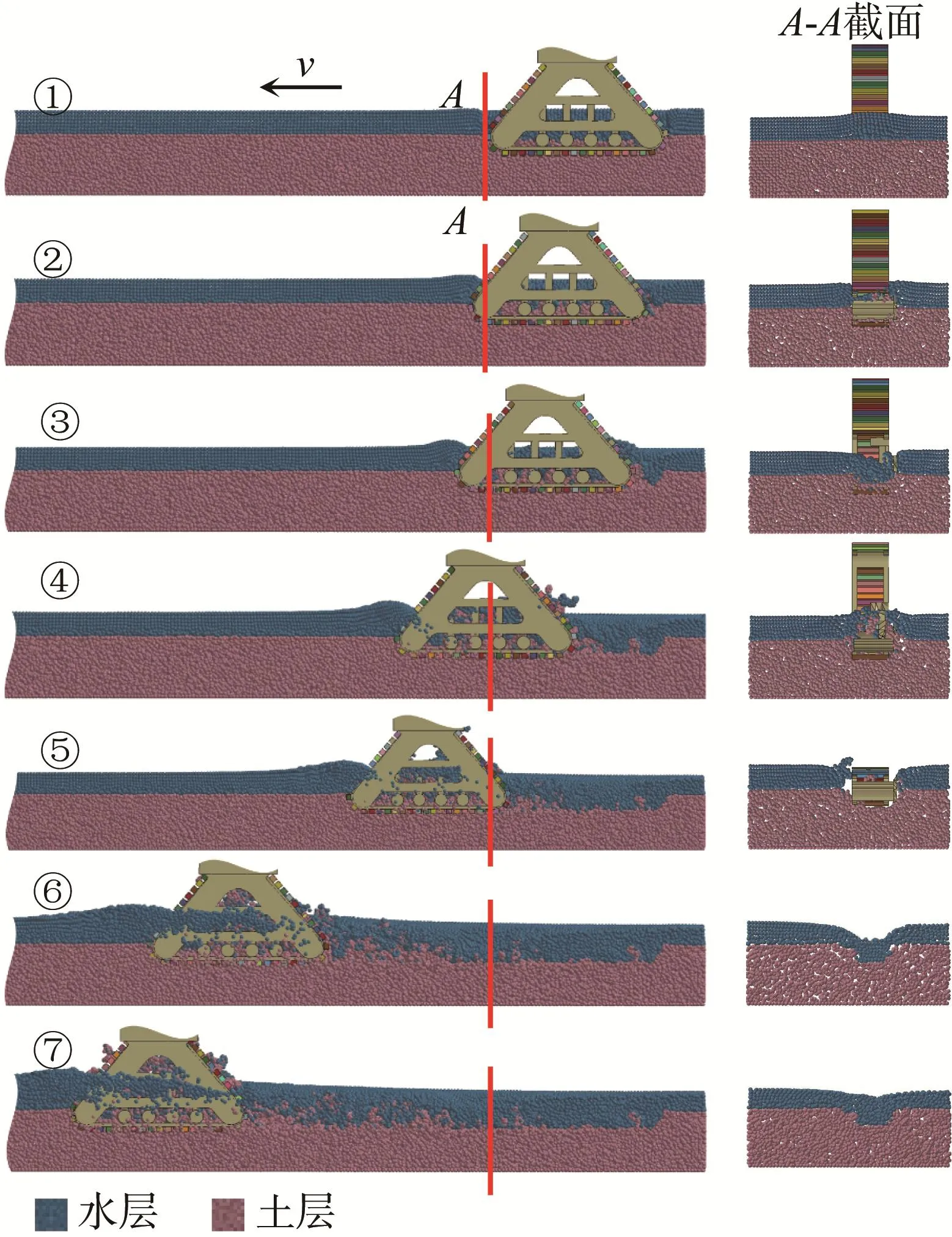
图5 机器人踩踏式除草过程仿真分析结果Fig.5 Simulation analysis result of robot pedaling weeding process
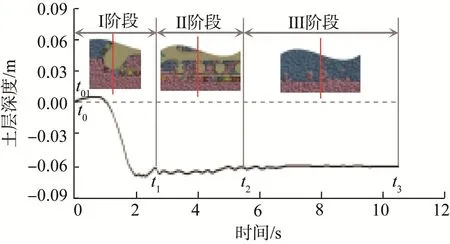
图6 机器人踩踏后A-A截面处土层深度随时间的变化情况Fig.6 Variation of soil layer depth at section A-A with time after robot pedaling
3.2 仿真结果分析
为便于后续比较,仿真分析时的参数设置与水田试验保持一致。分别在不同的机器人质量(M=52,57,62,67和72 kg)、运动速度(v=0.1,0.2,0.3,0.4和0.5 m/s)以及水层厚度(hw=0.02,0.03,0.04,0.05和0.06 m)下,对机器人踩踏式除草过程进行仿真分析。在仿真分析过程中,提取机器人踩踏前后多个位置的土层轮廓数据,并利用AutoCAD软件描绘土层轮廓,同时借助其填充功能统计不同位置处的土层面积和压痕面积(S0、S1和S2),并对其取平均值,以表征该次除草过程中土层的平均变形情况,然后将所得平均值代入式(1)以计算土壤扰动率δ1。同时,通过统计水土耦合模型中一定体积内离散状态的土壤颗粒数量n,结合式(2)计算水层密度增量δ2:
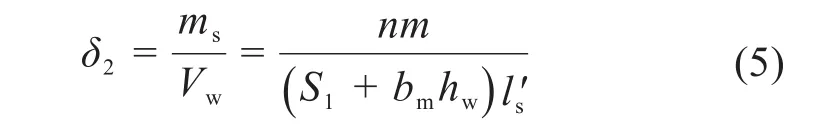
式中:m为单个土壤颗粒的质量;l′s为统计区域内水层的长度。
将基于仿真结果求得的土壤扰动率δ1和水层密度增量δ2代入式(3),求得综合评价函数φx的值,以对机器人踩踏式除草效果进行综合评价。
4 机器人踩踏式除草过程试验研究
4.1 试验方法
在水稻试验基地的水田试验槽内,利用踩踏式除草机器人进行除草试验,以分析不同因素对踩踏式除草效果的影响。试验用机器人样机如图7(a)所示,其履带的前、后倾角θ1=θ2=50°,接地长度L=0.42 m,质量M=52 kg;水田试验槽如图7(b)所示,其尺寸为7.4 m×1.4 m;根据试验槽中淤泥的情况,设ω1=0.25,ω2=0.75。机器人踩踏式除草试验采样原理如图8所示,通过获取机器人踩踏前后土层轮廓和水样,求得土壤扰动率δ1和水层密度增量δ2,从而对除草效果进行评价。为了减少随机误差,在距离机器人前轮初始位置0.5 m处设置采样点1,随后沿机器人前进方向,以1 m的采样间距再设置4个采样点,如图8(a)所示。采样过程如图8(b)所示,试验前将试验槽土面推平,放入清水调节水层厚度,待水层恢复平静、清澈后,采集初始水样;开始试验后,当机器人分别从各采样点完全经过且继续向前运动一定距离(0.5 m)后,在采样点插入无底隔水桶,每隔0.5 h采集一次水样,最后缓慢抽净桶内的浑浊泥水,并尽量使土层压痕不受影响,直到机器人踩踏的土层轮廓完全呈现;插入遇水变色试纸提取踩踏后的土层轮廓,以备后用。

图7 踩踏式除草机器人样机和水田试验槽Fig.7 Pedaling weeding robot prototype and paddy field test tank
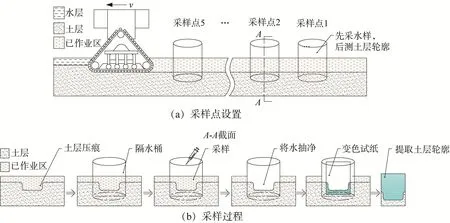
图8 机器人踩踏式除草试验采样原理Fig.8 Sampling principle of robot pedaling weeding experiment
4.2 试验结果分析
4.2.1 除草效果评价
利用AutoCAD软件分析提取的土层轮廓,将描绘得到的草图缩放至实际大小后统计踩踏前土层的初始面积S0以及踩踏后的土层压痕面积S1和剩余面积S2,如图9所示。为便于与仿真结果进行对比,将土层轮廓的尺寸沿边界扩充至0.60 m×0.23 m,并计算对应的土壤扰动率。

图9 土壤扰动率相关数据提取Fig.9 Relevant data extraction for soil disturbance rate
为了获取水层密度增量,将采取的水样摇晃均匀,用粗口针筒抽取10 mL水样,拍击针筒去除气泡,利用精密电子天平(EXD-322B,福州华科电子仪器有限公司生产)称取质量,得到机器人踩踏前后水层的平均密度ρ0、ρ1,并通过式(2)计算得到相应的水层密度增量。
图10(a)所示为机器人运动速度v=0.3 m/s,水层厚度hw=0.04 m,不同机器人质量M下的除草效果。由图可知,土壤扰动率δ1和水层密度增量δ2的试验值与仿真值的最大相对误差分别为18.617 5%和10.222 2%。图10(b)所示为机器人质量M=52 kg,水层厚度hw=0.04 m,不同机器人运动速度v下的除草效果。由图可知,δ1和δ2的试验值与仿真值的最大相对误差分别为15.299 6%和14.584 8%。图10(c)所示为机器人运动速度v=0.4 m/s,机器人质量M=52 kg,不同水层厚度hw下的除草效果。由图可知,δ1和δ2的试验值与仿真值的最大相对误差分别为14.850 2%和8.241 3%。
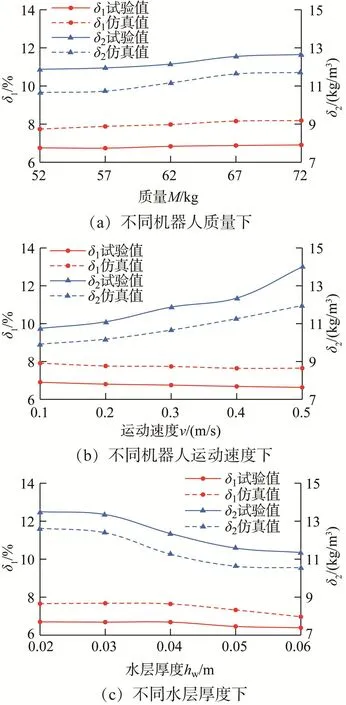
图10 机器人踩踏式除草效果比较Fig.10 Comparison of robot pedaling weeding effect
试验结果与仿真结果存在误差的原因主要是:设置的仿真参数较为理想化,而试验槽的实际土况复杂,深度方向上土层的物理性质不均匀,且表层淤泥较为松软,易回填至机器人踩踏的凹坑中,而仿真分析无法较好地模拟淤泥的高流动性,导致土壤扰动率δ1的仿真值大于试验值。此外,表层淤泥相对更容易被破坏,其大部分会溶入水中,而仿真分析无法较好地模拟淤泥的溶解情况,导致水层密度增量δ2的仿真值小于试验值。但总体而言,仿真结果与试验结果较为吻合,验证了仿真分析方法的可靠性。
此外,水层浊度可用于评价抑制光合作用效果的时效性。采用浊度传感器(RMD-Z6,深圳市瑞蒙德科技有限公司生产)分别对机器人踩踏后同一采样点不同时刻采集的水样进行浊度测量。为排除泥块的干扰,在水样自然沉降0.5 h后取上层部分进行浊度分析[25],并计算各采样点平均浊度随时间的变化关系,结果如图11所示。结果表明,机器人踩踏后5 h内水样浊度仍大于120 NTU,仍可明显抑制水下杂草的光合作用[26-28]。由此可知,间隔5 h踩踏1次,一天踩踏2次即可抑制水田杂草的生长。

图11 机器人踩踏后水层的浊度变化情况Fig.11 Turbidity change of water layer after robot pedaling
4.2.2 综合除草效果评价
当机器人运动速度v=0.4 m/s、水层厚度hw=0.04 m时,其综合除草效果随机器人质量M的变化曲线如图12(a)所示。当机器人质量M较小时,增大质量时其下陷量变化明显,则单位时间内踩踏的土壤增加,导致运动阻力增大,运动速度的波动增大,对土层的踩踏力度减弱,但总体上对综合除草效果的影响不大;随着机器人质量M的进一步增大,机器人在水田中的下陷量进一步增大,踩踏运动对土层的挤压切削效果变强;当机器人质量M较大时,下陷量接近水田的泥脚深度,质量改变对综合除草效果的影响减小。当机器人质量M=52 kg,水层厚度hw=0.04 m,其综合除草效果随运动速度v的变化曲线如图12(b)所示。随着v的增大,机器人踩踏时间变短,踩踏运动对水田土层、水层的挤压和冲击作用增强,易形成淤泥并溶入水中,使得综合除草效果增强。当机器人质量M=52 kg,机器人运动速度v=0.4 m/s,其综合除草效果随水层厚度hw的变化曲线如图12(c)所示。由于水对土壤的变形存在黏滞性和缓冲作用,当hw较小时,水层中的悬浮土壤颗粒浓度较高,可显著抑制杂草的生长,hw变化对综合除草效果的影响不明显;随着hw的增大,水层的缓冲作用增强,导致综合除草效果减弱。此外,从图12中还可以看出,仿真结果与试验结果也基本吻合,进一步验证了所构建模型的可靠性和所提出评价方法的可行性。
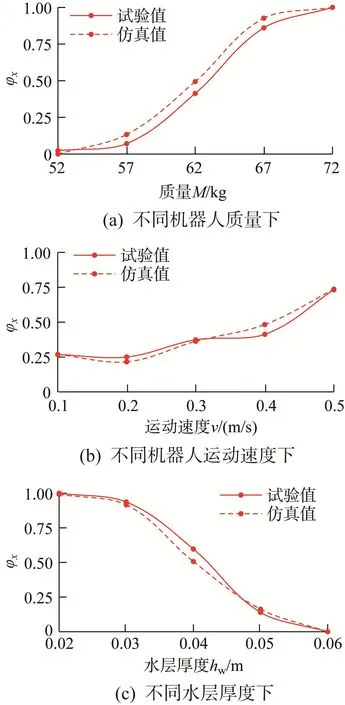
图12 机器人踩踏式综合除草效果比较Fig.12 Comparison of comprehensive robot pedaling weeding effect
5 机器人踩踏式除草过程的正交仿真试验
5.1 正交仿真试验设计
为进一步讨论机器人质量M、运动速度v和水层厚度hw对踩踏式除草效果的影响程度,采用三因素三水平正交试验进行仿真分析。根据上文得到的各因素对机器人踩踏式除草效果的影响情况,设计正交仿真试验因素水平表,如表1所示。

表1 机器人踩踏式除草过程正交仿真试验因素水平表Table 1 Factor level table for orthogonal simulation experiment of robot pedaling weeding process
5.2 正交仿真试验结果分析与讨论
基于L9(34)正交表,开展机器人踩踏式除草过程正交仿真试验,结果如表2所示。

表2 机器人踩踏式除草过程正交仿真试验结果Table 2 Orthogonal simulation experiment results of robot pedaling weeding process
为判断各因素对踩踏式除草效果的影响程度及其显著性,利用 SPSS(statistical product and service solutions,统计产品与服务解决方案)软件对上述正交仿真试验结果进行方差分析,结果如表3所示。当置信度a=0.05时,由基于校正模型的最小置信度P 表3 机器人踩踏式除草过程正交仿真试验结果方差分析Table 3 Variance analysis of orthogonal simulation experiment results of robot pedaling weeding process 为进一步得到机器人踩踏式除草效果最佳时的参数组合,依次统计各因素j在不同水平下的综合评价函数值之和Ki,j(j=M、v、hw;i=1,2,3),结果如图13所示。由图可知,随机器人质量M的增大,Ki,j增大;随着运动速度v的增大,Ki,j增大;随水层厚度hw的增大,Ki,j减小。由此可知,最优的参数组合为 M3v3hw1,即机器人质量M=72 kg,运动速度v=0.5 m/s、水层厚度hw=0.02 m时除草效果最佳。 图13 不同因素水平下机器人踩踏式除草效果比较Fig.13 Comparison of robot pedaling weeding effect under different factor levels 通过ANSYS/LS-DYNA软件中的SPH算法建立了机器人踩踏式除草过程的有限元模型,分析了机器人踩踏组件与水田土层、水层之间的相互作用,模拟了踩踏式除草的动态过程。结果表明,踩踏式除草的仿真过程与实际非常相似,验证了所构建有限元模型及其求解方法的正确性。分析了影响机器人踩踏式除草效果的因素,并提出了除草效果的综合评价方法。通过仿真和试验分析了机器人质量、运动速度和水层厚度对踩踏式除草效果的影响,并通过正交仿真试验分析了各因素对除草效果的影响程度。结果表明,基于ANSYS/LS-DYNA软件中的SPH算法能很好地模拟机器人在水田中的踩踏式除草动态过程;3个因素对机器人踩踏式除草效果影响的主次顺序为机器人运动速度、水层厚度、机器人质量,合理匹配各项参数,可以提升机器人的除草效果。本文提出的多相流建模方法同样适用于其他水田作业,研究结果为水田除草作业的动态仿真分析与评价提供了一种有效方法。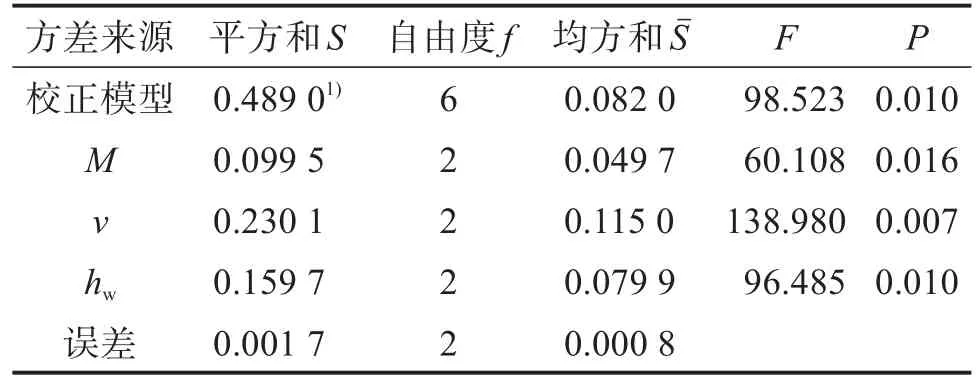

6 结论
