双弹簧电液激振缸振幅补偿性能的研究

赵凯平，何 涛,2,3，王传礼,2,3，史 瑞

（1.安徽理工大学机械工程学院，安徽淮南 232001；2.流体动力与机电系统国家重点实验室，浙江杭州 310027；3.矿山智能装备与技术安徽省重点实验室，安徽淮南 232001）

激振装置是利用机械、电动、电液等原理及电致或磁致伸缩效应进行驱动以产生机械振动的设备［1］，分为振动台和激振器两种类型。电液激振装置具有输出功率、位移和推力大，负载自适应及可控参数多等优点［2］，被广泛应用于工程机械［3-4］。随着现代工业技术的发展，对激振装置的振动频率范围提出了更高的要求［5-6］。对电液激振装置而言，如何在提高振动频率的同时增大振动幅值是电液激振技术发展的关键［7-8］。激振缸常被用作电液激振装置的执行机构，但是传统的激振缸的振幅会随着激振频率的提高而急剧衰减，且在谐振状态下激振缸的冲击波压力大，会产生噪声和破坏装置，难以满足现阶段工程试验的要求［9-11］。

针对上述问题，阮健等［12］设计了一种2D阀控电液激振器，其中2D阀阀芯的旋转运动和轴向滑动分别用于实现激振频率和幅值的独立控制，通过改变阀芯的转速、阀芯台肩一周的沟槽数以及该沟槽数与阀套一周的窗口数之间的配合关系来实现2D阀控电液激振器的高频激振。贾文昂等［13］指出，随着电液激振器激振频率的提高，激振力的输出会逐渐减小，但在某个频段激振力会突然增大，激振器在这一频段发生了谐振，即当工作频率与系统固有频率一致时，系统产生谐振现象，因此可以利用电液激振缸谐振点的谐振能量增大振动载荷或幅值，提高激振器的工作效率。王鹤等［14］设计了基于矩形、三角形、半圆形等不同阀口形状的阀芯旋转式电液激振器，分析了激振器的振动波形，其中具有矩形阀口的激振器相对来说可以获得振幅最大的振动波形，不过其加速度波动也最大。

目前，电液激振系统的优化大多着眼于优化电液激振阀［15-17］，或者利用电液激振系统的谐振来增大振动幅值。由于电液激振系统的执行机构是激振缸，这类优化方案的最终目的都是改变激振缸的输入、输出流量特性或自身谐振特性，且随着激振频率的提高电液激振阀阀口开启的时间必然会减少，因此优化效果并不明显。本文设计了一种双弹簧电液激振缸结构，从改变激振缸自身结构的角度来优化其振动特性；在分析激振缸工作原理的基础上建立其数学模型，并进一步建立AMESim仿真模型，研究激振缸活塞杆的位移及其振幅补偿性能。

1 双弹簧电液激振缸的工作原理及数学模型

2.1 激振缸的工作原理

双弹簧电液激振缸的工作原理如图1所示。补偿弹簧Ⅰ与左活塞和活塞杆紧固连接，激振缸左右两端结构完全对称。液压油进入激振缸左腔，推动左活塞右动，进而通过补偿弹簧Ⅰ推动活塞杆右动；通过激振阀的高频换向，活塞杆作周期性的往复运动，并输出振动波形。

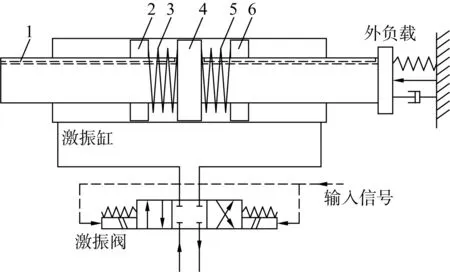
图1 双弹簧电液激振缸工作原理示意Fig.1 Schematic of working principle of double spring electro-hydraulic vibration cylinder

基于双弹簧电液激振缸的结构，分析激振缸活塞杆的右动过程。分析中忽略油液温度、黏度的变化及管路沿程圧力损失和局部压力损失，并假设液流状态为层流。

2.2 激振阀阀口的压力—流量方程

激振阀进、回油路阀口的流量方程为：

式中：q1、q2分别为流入、流出激振阀阀口的流量，m3/s；Cd为流量系数；Sv为激振阀阀口的面积梯度，m；xv为激振阀阀芯位移，m；ps为供油源压力，Pa；p1、p2分别为激振缸左、右腔的压力，Pa；ρ为液压油密度，kg/m3。

假设供油源压力ps恒定，令负载流量qL≈q1，负载压力pL=p1−p2≈p1（在活塞杆右动过程中p2≪p1），建立阀口线性化流量方程：

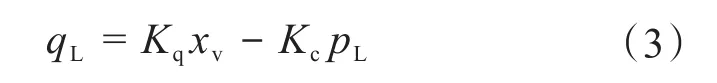
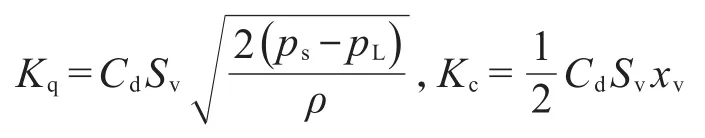
2.3 激振缸两腔的流量及运动方程

根据双弹簧电液激振缸的结构和工作原理，可得：

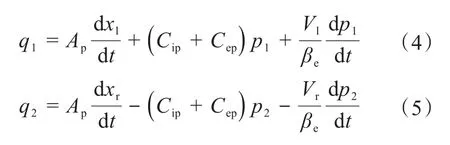
式中：Ap为活塞压力油的作用面积，m2；xl、xr分别为左、右活塞的位移，m；Cip、Cep分别为激振缸内、外泄漏系数，m3/（s·Pa）；Vl、Vr分别为激振缸左、右腔容积，m3；βe为油液有效体积弹性模量，Pa。

其中：

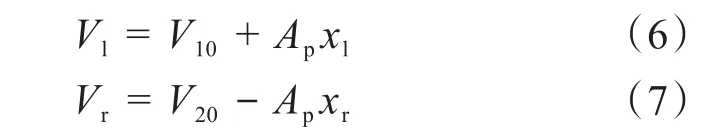
在初始状态，假设：

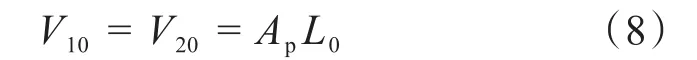
式中：V10、V20分别为激振缸左、右腔初始容积，m3；L0为激振缸左右腔初始长度，m。

由于xl、xr远小于L0，将其忽略并将式（8）代入式（6）和式（7），可得：Vl≈Vr≈ApL0。

根据负载流量和负载压力的定义，可得：

式中：ml、mr分别为激振缸左、右活塞的质量，kg；k1、k2分别为补偿弹簧Ⅰ、补偿弹簧Ⅱ的刚度，N/m；xp为活塞杆位移，m；me为活塞杆和折算到活塞杆上的总质量，即活塞杆等效质量，kg；Bp为外负载黏性阻尼系数，N·s/m；K为外负载弹簧刚度，m/s；FL为外负载力，N。

2.4 激振系统固有频率及振幅补偿机理分析

若忽略图1中的补偿弹簧Ⅰ、补偿弹簧Ⅱ和左右活塞，液压油直接作用在活塞杆上，则激振缸即为传统的电液激振缸。传统电液激振缸激振系统的固有频率是负载质量与液压缸工作腔中的油液压缩所形成的液压弹簧相互作用的结果［18-19］。假设激振缸是无摩擦、无泄漏的，在连续稳定的激振状态下可将传统电液激振缸近似为2个工作腔充满高压液体并被完全封闭，此时激振系统的固有频率为［20］：

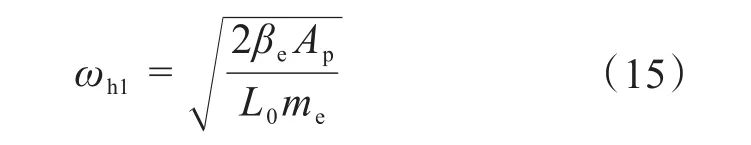
式中：ωh1为传统电液激振缸激振系统的固有频率，Hz。

由式（15）可知，在βe的影响下激振系统的固有频率非常高，在一般的激振频率范围内系统不会发生谐振。同时，传统电液激振缸处于谐振状态时产生的冲击波压力非常大，会产生噪声，破坏密封装置，影响整个激振系统的稳定性和安全性。

在双弹簧电液激振缸中，补偿弹簧的刚度远小于油液压缩所形成的液压弹簧的刚度，故在考虑双弹簧电液激振缸激振系统的固有频率时，忽略液压弹簧对激振缸固有频率的影响，可得激振缸固有频率近似为：

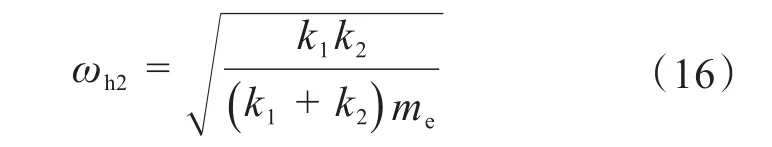
式中：ωh2为双弹簧电液激振缸激振系统的固有频率，Hz。

由式（16）可知，双弹簧电液激振缸激振系统的固有频率与补偿弹簧的刚度有关。当激振频率与系统的固有频率一致或相近时，激振缸发生谐振，其输出的位移振幅会大幅度增大。由于双弹簧电液激振缸发生谐振时激振频率较小，与油液压缩所形成的液压弹簧的刚度无关，不会给激振系统带来不利影响，同时，激振系统的固有频率可调节且范围宽，理论上可以将双弹簧电液激振缸谐振特性应用于电液激振缸的振幅补偿。鉴于液压弹簧刚度实际上并不存在，双弹簧电液激振缸激振系统的固有频率无法求得准确值，以下将结合激振系统传递函数作进一步分析。

2.5 激振系统传递函数

当 FL=0 N，Bp、ml、mr较小可以忽略不计时，对式（3）、式（11）至式（14）进行拉普拉斯变换，求解得到激振系统传递函数：

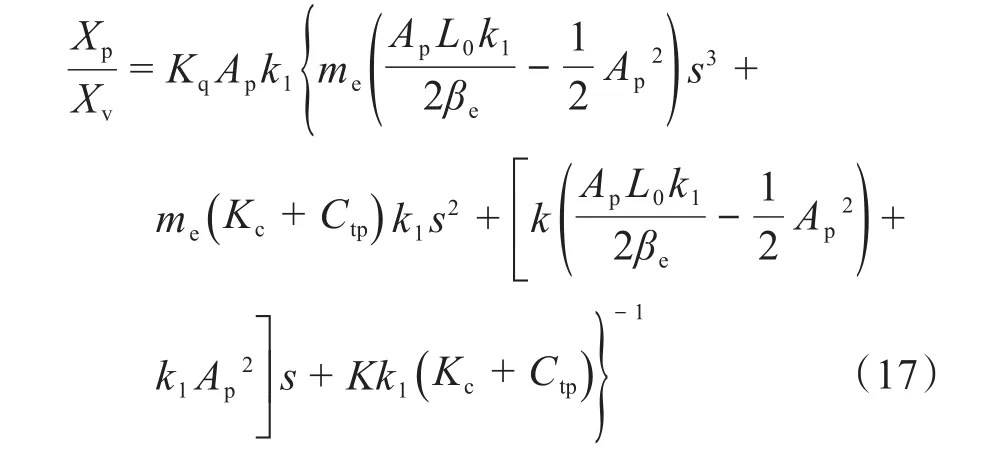
根据式（17）分析系统参数变化对系统输出响应的影响。由于βe较大，一般取βe=8.0×106Pa，故在一定范围内可以忽略L0对输出位移的影响。外部参数确定后，在激振缸活塞杆右动过程中xp与k2无关，且增大k1可以改变活塞杆位移的输出特性，但两者并不呈正相关或负相关关系。由于k1过大或过小均会使液压缸失去振幅补偿性能，故有必要对k1的取值进行探讨。活塞杆位移同时受到外部负载、摩擦力等的影响。由于传递函数并不能对系统的内部结构进行完整描述，只能直接表达系统在油液输入和输出过程中可测量的参数的变化，故对激振系统进行更为完整的仿真分析。

3 传统和双弹簧电液激振缸振幅补偿仿真分析与比较

3.1 激振系统仿真模型

根据电液激振缸的结构和工作原理，结合其数学模型，利用AMESim仿真软件建立传统和双弹簧电液激振缸激振系统的仿真模型，分别如图2、图3所示，对比分析两者的活塞杆输出特性。

图2 传统电液激振缸激振系统仿真模型Fig.2 Simulation model of excitation system of traditional electro-hydraulic vibration cylinder

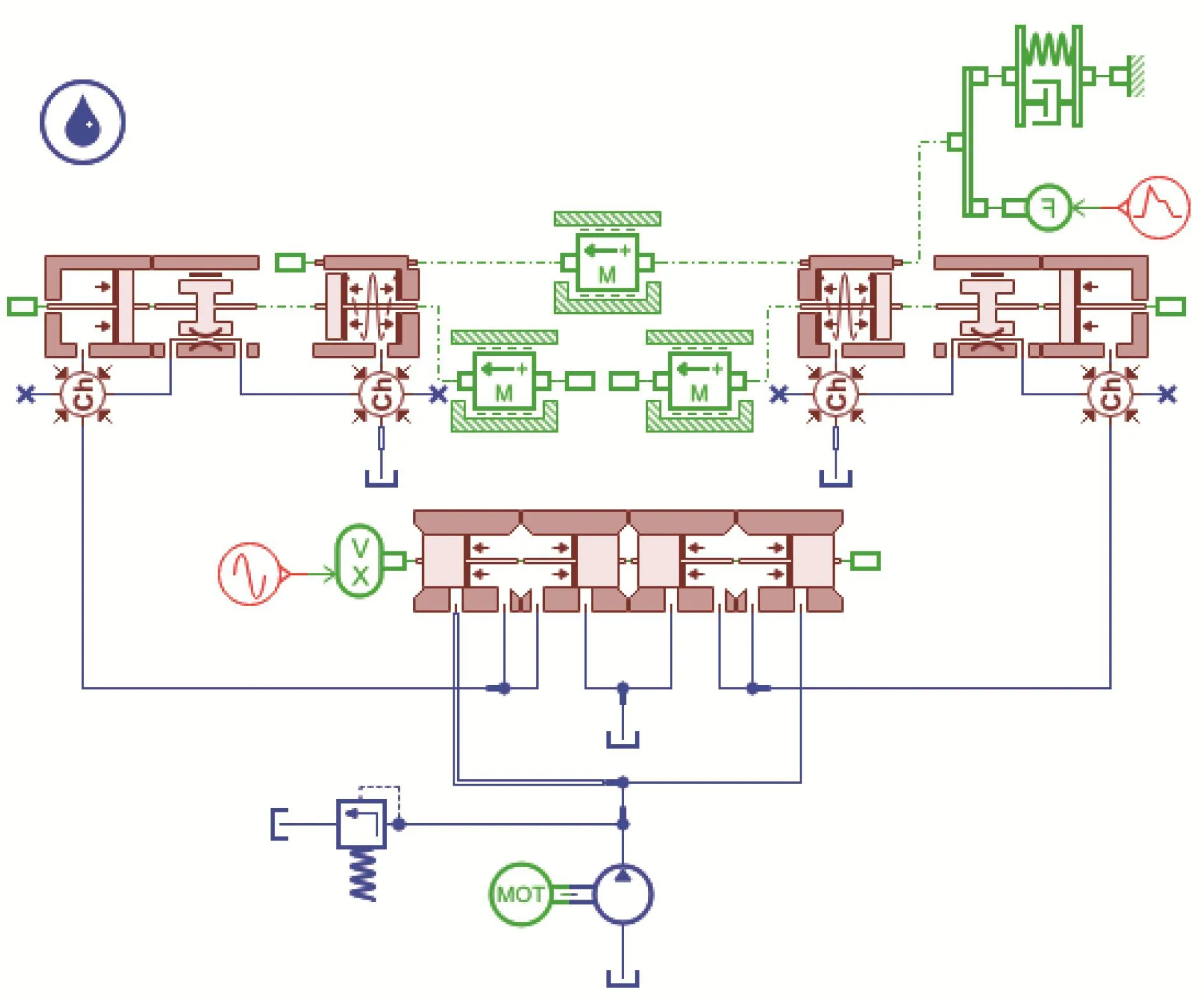
图3 双弹簧电液激振缸激振系统仿真模型Fig.3 Simulation model of excitation system of double spring electro-hydraulic vibration cylinder

为便于分析与比较，传统和双弹簧电液激振缸激振系统仿真模型中相同元件的参数设置一致，双弹簧电液激振缸补偿弹簧Ⅱ的刚度k2与补偿弹簧Ⅰ的刚度k1设置为相同。仿真中用到的主要参数见表1。

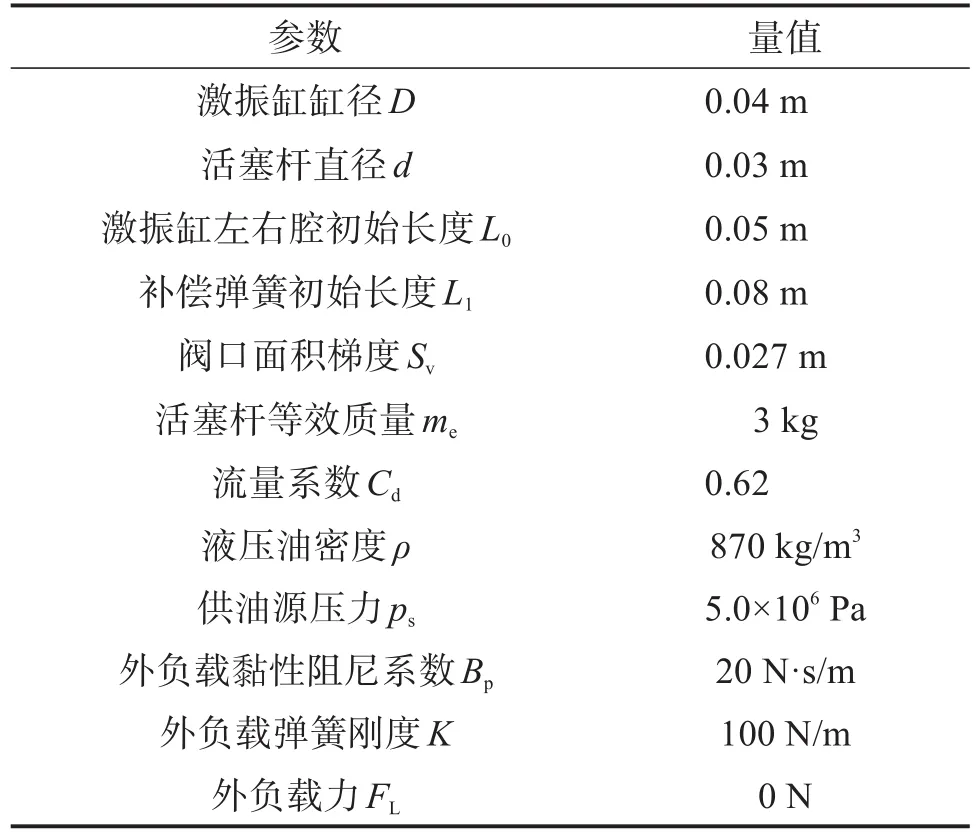
表1 电液激振缸激振系统仿真模型的主要参数Table 1 Main parameters of simulation model of excitation system of electro-hydraulic vibration cylinder

3.2 激振缸活塞杆的位移

设置k1=14 N/mm，激振频率f=20 Hz，仿真时间t=6 s。传统和双弹簧电液激振缸活塞杆的位移曲线如图4所示，图5为图4的局部放大图。补偿弹簧Ⅰ的长度响应曲线如图6所示。

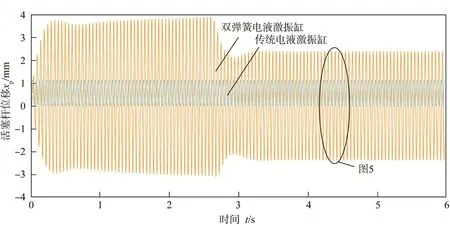
图4 传统和双弹簧电液激振缸活塞杆位移曲线Fig.4 Displacement curve of piston rod of traditional and double spring electro-hydraulic vibration cylinder

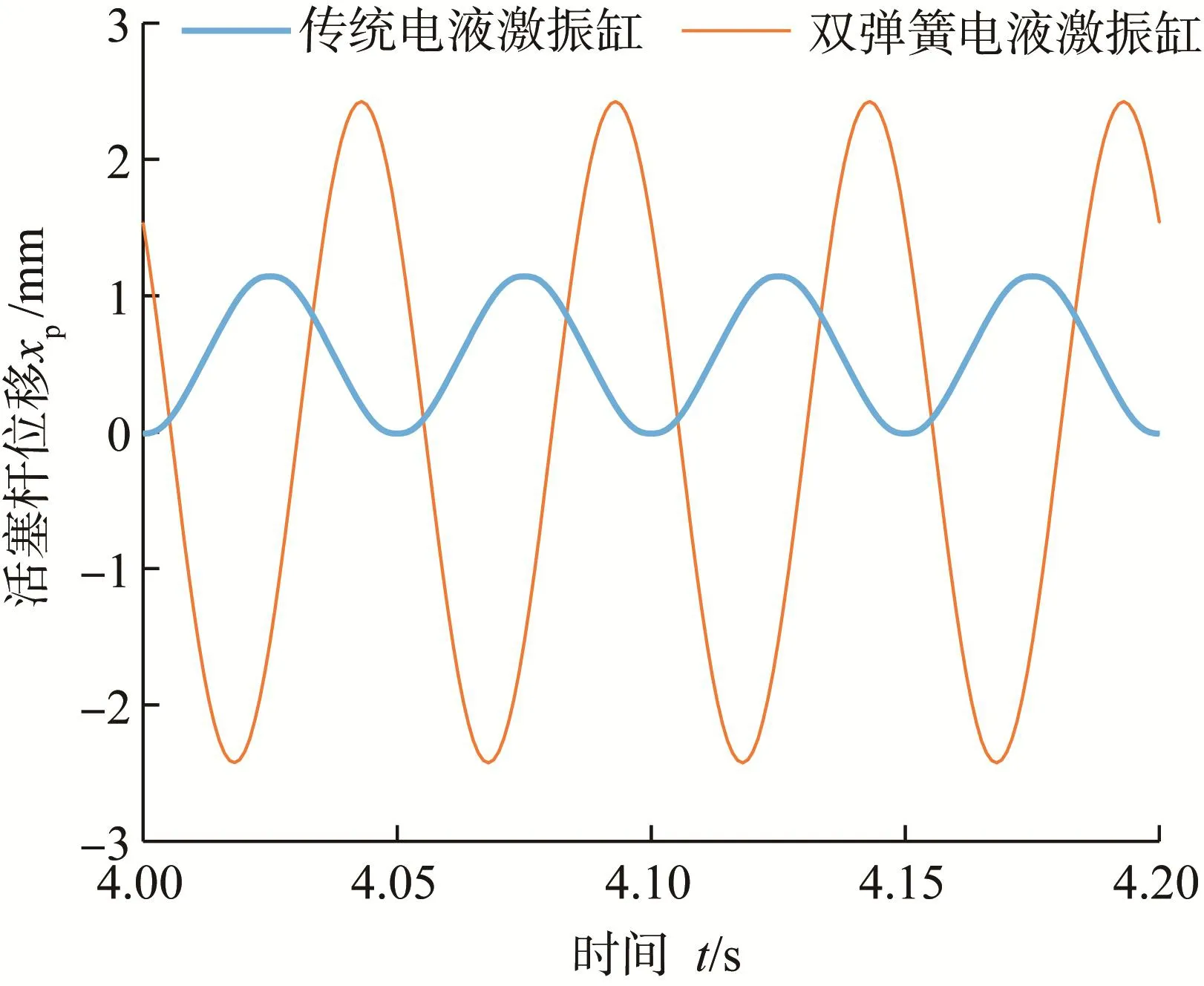
图5 图4的局部放大图Fig.5 Partial enlarged schematic diagram of fig.4

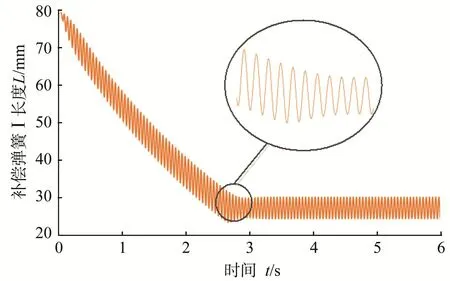
图6 补偿弹簧Ⅰ的长度响应曲线Fig.6 Length response curve of compensation spring I

由图4和图6可知：双弹簧电液激振缸的振幅中心趋近于活塞杆零位移点，偏离激振缸初始激振中心；其活塞杆的位移振幅分为振荡区和稳定区，经过3 s后振荡逐渐趋于稳定，在稳定区的振幅为2.42 mm，比传统电液激振缸的0.57 mm大许多；位移振幅在初始时刻较小，随后迅速增大，这是由于在初始时刻双弹簧电液激振缸的左腔压力较小，且存在外部负载，在补偿弹簧的缓冲作用下振幅较小；在0.3—2.7 s内位移振幅较大，达到约3.50 mm，这是由于在此时间段补偿弹簧振荡激烈，此时补偿弹簧宏观形变量（补偿弹簧由于振荡偏移所产生的累积形变量）不断增大，并且在增大的过程中补偿弹簧自身也存在激振现象；在2.7—3.0 s内位移振幅降低，后趋于稳定，这是由于补偿弹簧逐渐恢复稳定，其宏观形变量稳定在50 mm左右；在3.3—6.0 s内位移振幅稳定在2.42 mm，这是由于虽然补偿弹簧的宏观形变量趋于稳定，但在小范围内形变量仍以正弦波形不断振荡，其振幅为2.70 mm，激振系统的固有频率与此时的激振频率相一致或接近，系统发生谐振，振幅相比于传统电液激振缸有大幅度增大，从而取得了振幅补偿的效果。

3.3 不同激振频率下激振缸活塞杆的位移

设置k1=16 N/mm，f=16～24 Hz，t=6 s，步长为2。得到不同激振频率下传统和双弹簧电液激振缸活塞杆的位移曲线，如图7所示。

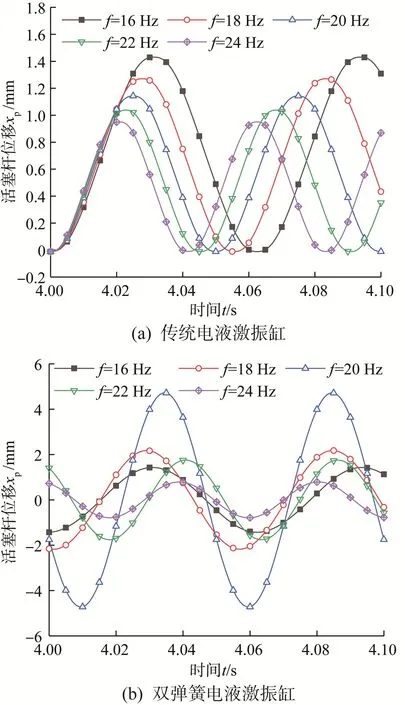
图7 不同激振频率下传统和双弹簧电液激振缸活塞杆位移曲线Fig.7 Displacement curves of piston rod of traditional and double spring electro-hydraulic vibration cylinder under different excitation frequencies

由图7（a）可知，随着激振频率从16 Hz递增到24 Hz，传统电液激振缸活塞杆的位移不断递减。这是由于随着激振频率的提高，在一个激振阀换向周期内阀口的开启时间减少，进而直接导致流入激振缸的流量减小。

由图7（b）可知，双弹簧电液激振缸不同于传统电液激振缸，其活塞杆位移不与激振频率呈简单的正相关或负相关关系。随着激振频率从16 Hz递增到20 Hz，活塞杆位移不断增大；随着激振频率从20 Hz递增到24 Hz，活塞杆位移不断减小；随着激振频率从18 Hz递增到20 Hz或从20 Hz递增到22 Hz，活塞杆位移增大或减小的幅度较大；当激振频率为16 Hz或24 Hz时，振幅补偿效果较差。可知当k1=16 N/mm时，f=20 Hz为最优频率。

3.4 不同补偿弹簧刚度下双弹簧电液激振缸活塞杆的位移

设置k1=14～18 N/mm，f=20 Hz，t=6 s，步长为1。得到不同补偿弹簧刚度下双弹簧电液激振缸活塞杆的位移曲线，如图8所示。

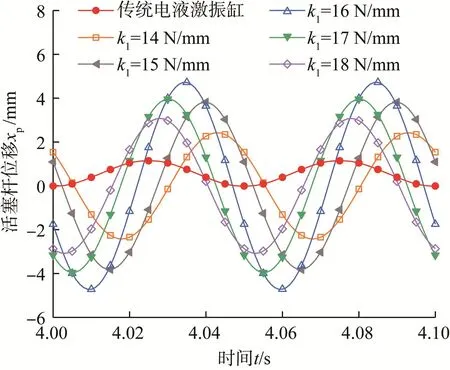
图8 不同补偿弹簧刚度下双弹簧电液激振缸活塞杆位移曲线（f=20 Hz）Fig.8 Displacement curve of piston rod of double spring electro-hydraulic vibration cylinder under different compensation spring stiffness(f=20 Hz)

由图8可知：随着补偿弹簧Ⅰ的刚度从14 N/mm递增到16 N/mm，双弹簧电液激振缸活塞杆的位移不断增大；随着补偿弹簧Ⅰ的刚度从16 N/mm递增到18 N/mm，活塞杆位移不断减小；当k1=16 N/mm时，活塞杆位移达到最大值，为4.70 mm，相比于传统电液激振缸的0.57 mm，增大了4.13 mm。可见，补偿弹簧刚度对双弹簧电液激振缸活塞杆的位移振幅有较大影响，且当f=20 Hz时，k1=16 N/mm为补偿弹簧Ⅰ最优刚度，可以使激振缸活塞杆的位移振幅达到最大。

设置k1=21～25 N/mm，f=24 Hz，t=10 s，步长为1。得到不同补偿弹簧刚度下双弹簧电液激振缸活塞杆的位移曲线，如图9所示。

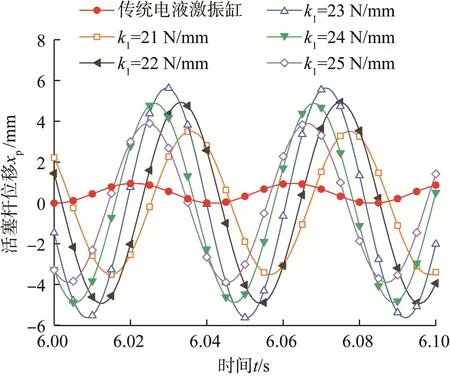
图9 不同补偿弹簧刚度下双弹簧电液激振缸活塞杆位移曲线（f=24 Hz）Fig.9 Displacement curve of piston rod of double spring electro-hydraulic vibration cylinder under different compensation spring stiffness(f=24 Hz)

由图9可知，当f=24 Hz时双弹簧电液激振缸活塞杆位移曲线的变化规律与f=20 Hz时类似。所不同的是，当k1=23 N/mm时，活塞杆的最大位移振幅为5.60 mm，相比于传统电液激振缸的0.48 mm，增大了5.12 mm。即当f=24 Hz时，k1=23 N/mm为补偿弹簧Ⅰ最优刚度，可以使激振缸活塞杆的位移振幅达到最大。

设置k1=29～33 N/mm，f=28 Hz，t=10 s，步长为1。得到不同补偿弹簧刚度下双弹簧电液激振缸活塞杆的位移曲线，如图10所示。

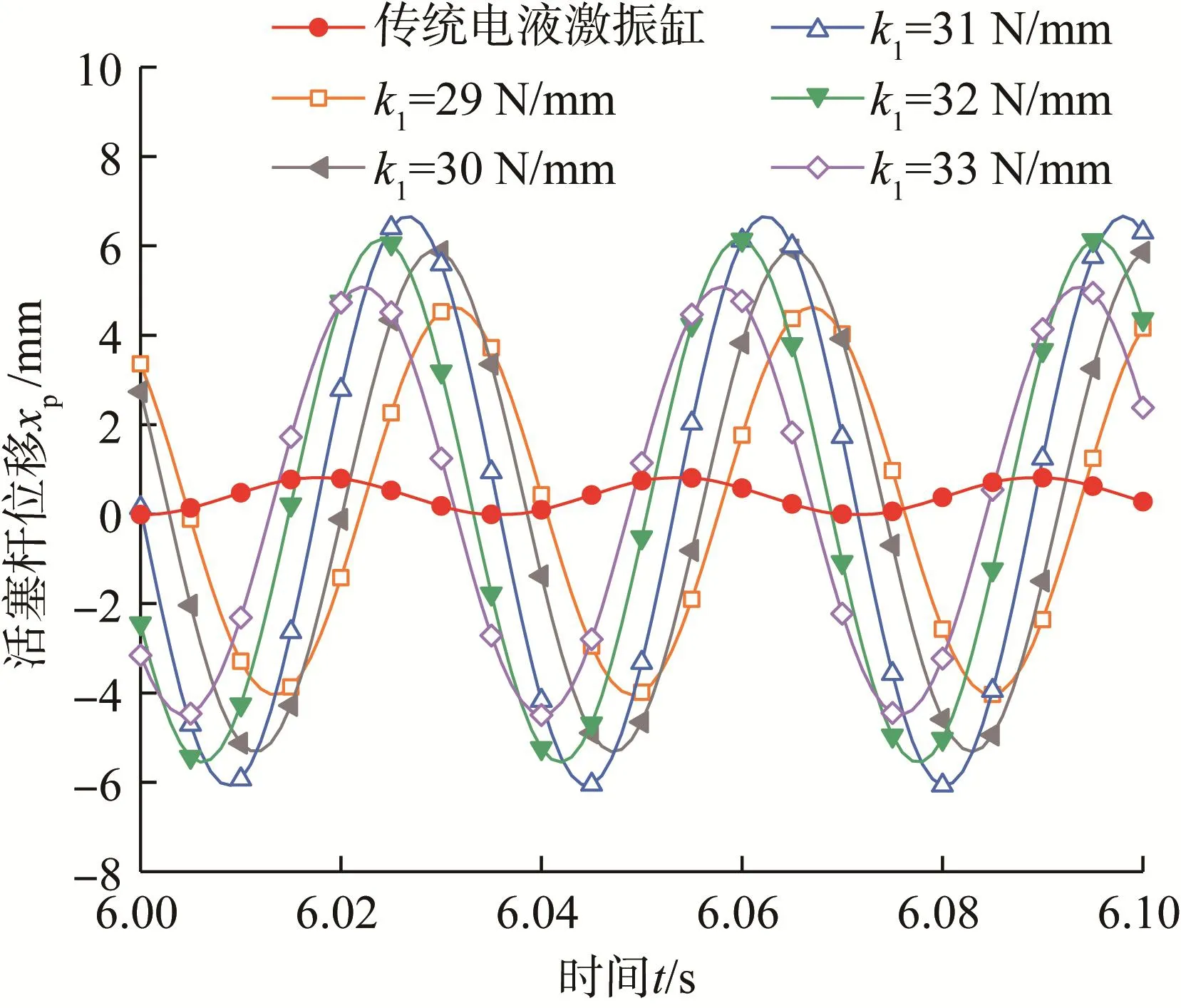
图10 不同补偿弹簧刚度下双弹簧电液激振缸活塞杆位移曲线（f=28 Hz）Fig.10 Displacement curve of piston rod of double spring electro-hydraulic vibration cylinder under different compensation spring stiffness(f=28 Hz)

由图10可知，当f=28 Hz时双弹簧电液激振缸活塞杆位移曲线的变化规律与f=20，24 Hz时类似。所不同的是，当k1=31 N/mm时，活塞杆的最大位移振幅为6.65 mm，相比于传统电液激振缸的0.41 mm，增大了6.24 mm。即当f=28 Hz时，k1=31 N/mm为补偿弹簧Ⅰ最优刚度，可以使激振缸活塞杆的位移振幅达到最大。

综上所述，可得不同激振频率下传统和双弹簧电液激振缸的振幅补偿，如表2所示。

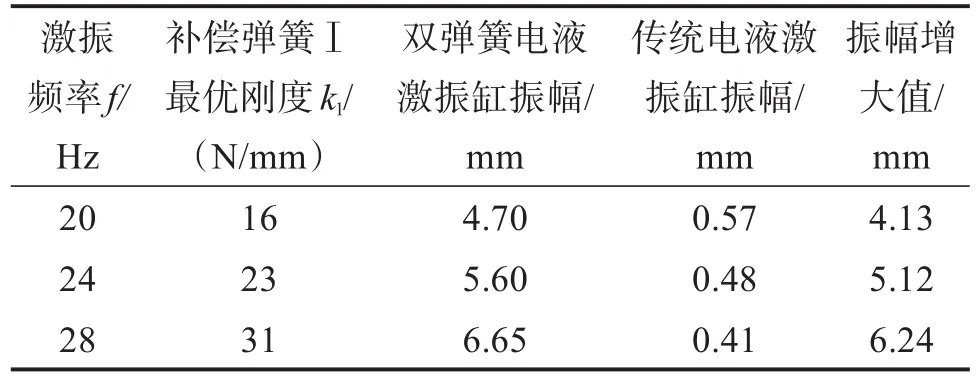
表2 不同激振频率下传统和双弹簧电液激振缸的振幅补偿Table 2 Amplitude compensation of traditional and double spring electro-hydraulic vibration cylinders under different excitation frequencies

根据以上分析可知：不同的激振频率对应不同的补偿弹簧最优刚度，使得振幅补偿效果达到最优；在一定激振频率范围内，随着激振频率的提高，传统电液激振缸的位移振幅减小，而双弹簧电液激振缸的位移振幅增大；随着激振频率的提高，补偿弹簧刚度应相应增大，才能使双弹簧电液激振缸具有最好的振幅补偿性能，这对补偿弹簧的材质和刚度提出了更高的要求。

4 总 结

1）针对传统电液激振缸随着激振频率的提高，振动幅值急剧衰减的问题，设计了一种双弹簧激振缸结构，建立了其数学模型和AMESim仿真模型，分析了激振缸激振系统的静、动态特性。结果显示，在一定激振频率范围内，双弹簧激振缸具有良好的振幅补偿性能。当激振频率为28 Hz、弹簧补偿刚度为31 N/mm时，可使位移振幅增大6.24 mm，相比同一条件下传统电液激振缸的位移振幅提高了15倍多。

2）在工作过程中，双弹簧电液激振缸的位移振幅存在振荡区和稳定区，振荡区时长与弹簧刚度和激振频率有关，与补偿弹簧宏观形变量达到最大值所需的时间基本一致。稳定区内的移动振幅较小，振幅大小直接决定了双弹簧电液激振缸振幅补偿性能的优劣。

3）不同于传统电液激振缸，双弹簧电液激振缸在补偿弹簧刚度一定的情况下，其振幅不与激振频率呈简单的正相关或负相关关系，而在某一激振频率下谐振现象最明显，可使振幅补偿效果达到最优。

4）对于双弹簧电液激振缸，激振频率不同，则补偿弹簧最优刚度不同，且随着激振频率的提高，补偿弹簧刚度应相应增大，才能取得最好的振幅补偿效果。随着激振频率的大幅度提高，对补偿弹簧的刚度和材质提出了更高的要求。