基于人工鱼群算法-极限学习机的多手势精准识别

来全宝，陶 庆，胡玉舸，孟庆丰

（新疆大学机械工程学院，新疆乌鲁木齐 830047）

随着我国老龄化人口数量的急剧增加，因中风而偏瘫的患者逐年递增。根据临床实践，患者主动积极地参与康复训练对其受损神经系统功能康复有重要作用［1］。为了提高患者主动训练的积极性以及解决人工协助的上肢手部康复训练治疗的长期性和单一性问题，通过提取并解码人体表面肌电信号（surface electromyography，SEMG）来获取患者的训练意图，并将其融入上肢手部康复训练器，这有利于大脑神经的重塑，从而促进肢体的康复。手势的精准识别是利用康复机器人进行训练的首要条件，因此探究手势识别方法的多样性和准确性是十分有必要的。肢体肌肉收缩产生的肌电信号中蕴藏着大量与神经活动有关的信息，且具有较高的信噪比。人体上肢运动方式不同，对应运动肌肉产生的肌电信号也有所不同，故可通过提取某些特征信号来对肢体的运动模式进行分类。目前，关于利用肌电信号对人体动作模式进行识别的研究已取得较多成果，但针对手势识别的研究仍不够深入，且大部分研究仅集中于少量手势的识别。例如：赵诗琪等［2］结合Fisher Score特征降维方法与机器学习对4种手势进行了识别，识别准确率为99.24%；Zhang等［3］运用神经网络对5种手势进行了识别，平均识别准确率达98.7%；Yang等［4］运用高斯混合模型-隐马尔可夫模型（Gaussian mixture model-hidden Markov model，GMM-HMM）识别了6种手势，识别准确率达99%。随着手势种类的增多，各分类模型的识别准确率有所下降［5］。例如：Guo等［6］对8种人体上肢动作进行了识别，平均识别准确率仅为73.1%～97.7%；Leon等［7］结合时频域特征对9种手势进行了识别，识别准确率仅为94%；Lian等［8］采用K最近邻和决策树算法对10种手势进行了识别，平均识别准确率仅为89%；Schabron等［9］采用神经网络对9种手势进行了识别，最高识别准确率为90.3%；Liang等［10］通过结合原始肌电信号和包络信号，基于监督学习和单变量特征对9种手势进行了识别，最高识别准确率为95%。综上所述，多手势识别的准确率还有待提高，为进一步满足患者肢体康复的需求，研究准确率高的多手势识别方法十分重要。现阶段的手势识别大多是先通过采集受试者的SEMG以提取简单的时域、频域或时频域特征，然后采用反向传播（back propagation，BP）神经网络［11］、支持向量机（support vector machine，SVM）［12］和极 限学习 机（extreme learning machine，ELM）［13］等分类模型进行识别。但上述方法均存在不足之处，其中：BP神经网络在识别手势时存在准确率低的劣势；SVM具有很多未知参数，其在手势识别训练时需要大量样本来进行参数辨识；ELM与传统的单隐层前馈神经网络（singlehidden layer feedforward neural network，SLFN）相比，具有运算速度快、识别精度高等优点，但ELM的随机性对其泛化性和精度有较大影响［14］。

基于此，笔者综合ELM的随机性以及特征组合和滑动窗口等对数据样本的影响，选取最优特征组合与最优滑动窗口，提出一种基于人工鱼群算法（artificial fish swarms algorithm，AFSA）优化的ELM的多手势精准识别方法，以提高多手势识别准确率。首先，选取通过主成分分析（principal components analysis，PCA）降维处理后的最优特征组合与最优滑动窗口；然后，采用AFSA搜寻ELM的最优输入权值和隐含阈值，以提高其分类准确率；最后，利用AFSA优化的ELM（AFSA-ELM）分类模型对8种手势进行识别，并与BP神经网络分类模型和未优化的ELM分类模型进行比较，以验证所提出方法的精准性。

1 AFSA优化ELM

1.1 AFSA介绍

AFSA是一种通过设立人工鱼群模拟真实鱼群的觅食、聚群和追尾等行为，由局部到全局逐步寻优，最终得到整体最优解的算法。图1所示为人工鱼的视野V和移动步长S示意图。当人工鱼视野范围内位置XV处的食物浓度大于当前位置X处时，人工鱼将向前一步到达位置Xm处；否则向视野范围内的其他位置（如XV1和XV2）进行搜索。

图1 人工鱼视野和移动步长示意Fig.1 Schematic diagram of visual field and moving step of artificial fish

如图1所示，n条人工鱼的当前位置X=(x1，x2，…，xn)，其视野范围内的某一位置 XV=(xV1，xV2，…，xVn)，则搜寻过程可表示为：

式中：random（−1，1）为［−1，1］内的随机数。

1.2 ELM参数优化

ELM是一种全连接单隐层网络，分为输入层、隐含层和输出层，各层神经元的数量分别为w、l和p。将ELM训练过程简化成矩阵求逆问题，以有效提升其学习速度。ELM的网络结构如图2所示。

图2 ELM的网络结构Fig.2 Network structure of ELM

根据图2，ELM分类模型可表示为：

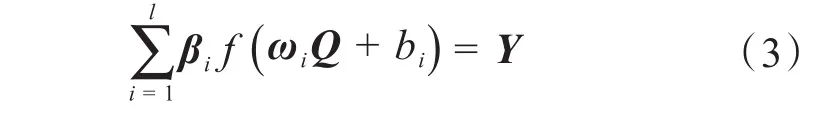
式中：βi为第i个隐含层到输出层的权值；f()为隐含层激活函数；ωi为输入层到第i个隐含层的权值，即输入权值；bi为第i个隐含层节点的阈值，即隐含阈值；Q为训练样本的输入，Q=（q1，q2，…，qw）T；Y为训练样本的输出，Y=（y1，y2，…，yp）T。

ELM固有的随机性是指在构建ELM分类模型时，其输入权值和隐含阈值是通过程序随机选取的，从而导致分类结果不理想。本文采用AFSA来优化ELM的参数，以构建最优的AFSA-ELM分类模型。具体流程如下：将ELM的输入权值和隐含阈值作为AFSA的搜寻个体，将ELM的训练样本期望输出与实际输出的均方根误差作为AFSA的适应度函数，得到的适应度函数值越小表明优化后的输入权值和隐含阈值越理想，即得到的AFSA-ELM分类模型越优，识别准确率越高。利用AFSA优化ELM参数的具体流程如图3所示。其中：σ为拥挤度因子，T为尝试次数，d为迭代次数，D为最大迭代数。

图3 AFSA优化ELM参数的具体流程Fig.3 Specific process of ELM parameters optimized by AFSA

2 SEMG采集与预处理

2.1 SEMG采集

采用葡萄牙Plux公司生产的八通道无线表面肌电测量系统和上海励图医疗器材有限公司生产的LT-7型理疗电极片，利用5个信号通道对4名在校大学生（2名男性，2名女性，年龄为（20±3）岁，手部正常均无骨折受伤经历）进行SEMG采集，分别对握拳、展拳、伸一指、伸两指、伸三指、伸四指、六手型和八手型等8种常用手势对应的SEMG进行采集。具体的实验过程如下：实验开始前，预先清洁受试者皮肤并用医用酒精擦拭相关肌肉群，然后将表面肌电测量系统的电极片（采样频率为1 000 Hz）粘贴在受试者左臂皮肤表面的5个位置处，分别为指浅屈肌、肱桡肌、指伸肌、尺侧腕伸肌和肱侧腕屈肌处；实验开始后，令受试者肘部搭在办公桌上，前臂和手部保持竖直放松，按照提示分别做上述8种手势，且做相同手势时保持手部姿态和力度大小、方向一致，对不同手势下的SEMG进行采集。对每名受试者采集20组信号，共采集80组数据；每采集4组信号休息5 min，以保证数据不受疲劳等因素的影响。其中1名受试者的手势识别实验现场如图4所示。鉴于各受试者前期经过多次训练，男性与女性的动作姿态、力度控制较为一致，各受试者间差异性较小。

图4 手势识别实验现场Fig.4 Gesture recognition experiment site

2.2 SEMG预处理

SEMG的频率一般为0～500 Hz，且主要频率为10～300 Hz，其容易受到噪声的干扰，故须对SEMG进行去噪处理，旨在调整基线漂移、去除频率较高的噪声信号以及消除50 Hz工频干扰的影响。在本文中，首先去除50 Hz工频干扰的影响，然后采用四阶巴特沃斯带通滤波器滤除基线噪声的干扰，滤波器的带通频率取30～150 Hz。在完成滤波操作后，采用活动段检测技术截取做手势时的SEMG，即截取肌肉收缩发力时（活动段）的SEMG，与活动段相对应的是肌肉处于静息放松状态下的非活动段。只有准确标记活动段的起止点，才能有效提取信号以识别手势。本文采用滑动窗口法对SEMG进行处理，窗口总长度为128 ms，滑动窗长度为64 ms，活动段起止点的判断阈值由多次测试确定，即取5个采样通道平均能量和最大值的0.06h倍（h为经验取值）；采用连续5次超越阈值法来确定活动段的起止点，为避免截取活动段信号时丢失有效的信号，在活动段起止点前后进行数据补充，以最大限度地保留有效信号。图5所示为八手型手势对应的活动段SEMG截取结果，其中采样点数被压缩了64倍。

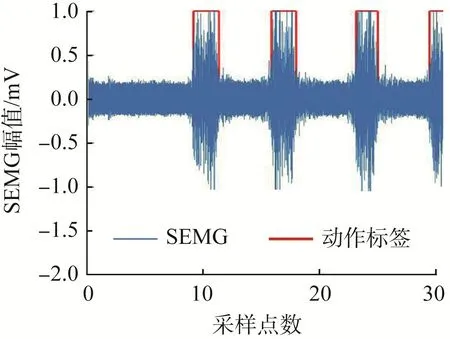
图5 八手型手势对应的活动段SEMG截取结果Fig.5 SEMG interception results of active segment corresponding to eight-hand gesture

3 组合特征提取与滑动窗口优化

仅经过预处理的SEMG是无法用于手势识别的，须提取可表征不同手势之间的特点和区别的有用信息，这些有用信息统称为特征，多个特征组合成特征向量。目前，被广泛使用的SEMG特征的提取方法有以下几种：时域特征提取、频域特征提取和时频域特征提取等。其中时域特征提取便捷，计算迅速，信息量大且全面，故本文以时域特征为研究对象，即分别提取SEMG的平均绝对值（mean absolute vlaue，MAV）、均方根值（root mean square，RMS）、方差（variance，VAR）和波形长度（waveform length，WL）等4个特征值，以从强度、波动性等不同方面来描述SEMG。上述4个特征值的计算式分别为：

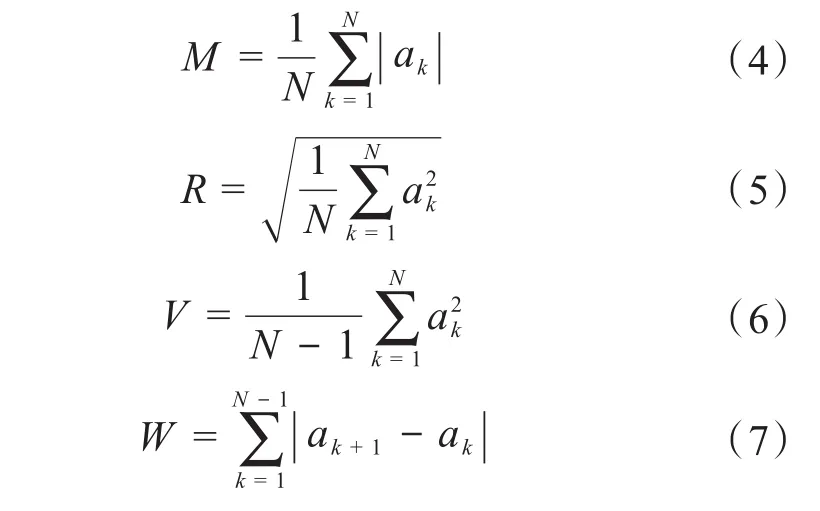
式中：M、R、V和W分别为平均绝对值、均方根值、方差和波形长度；N为活动段内有效的采样点数；ak为活动段内第k个采样点的SEMG幅值。

3.1 特征组合的优化选择

在手势识别中，对特征进行优化组合与降维处理可显著提高手势识别准确率。通过分析可知，基于时域特征的手势识别准确率偏低，而综合了频域特征与时频特征的识别效果也依然不佳。考虑到SEMG的非线性与混沌性，本文引入非线性特征——样本熵E［2］，样本熵的维数为2。每个通道提取5个特征（4个时域特征和1个样本熵），则5个通道信号的特征组合成一个25维的特征向量P，可表示为：

向量维度过大时存在信息冗余，使得计算时间过长，可用性比较差。本文采用PCA对上述25维特征向量进行降维处理，提取主成分后按贡献率进行排序，并选取贡献率最大的前3列主成分，从而将25维降到3维。基于上述方法，对8个手势对应的SEMG的特征组合进行优化选择，结果如图6所示，图中x、y、z分别对应前3列主成分。其中，图6（a）为基于PCA降维处理的时域特征散点图，图6（b）为基于PCA降维处理的样本熵散点图，图6（c）为基于PCA降维处理的时域特征和样本熵散点图。从图中可以清晰地看出，采用图6（c）方案时8个手势的特征可被明显区分，同时可缩短运算时间。

图6 不同手势对应的特征散点图Fig.6 Feature scatter diagram corresponding to different gestures

3.2 滑动窗口优化处理

在完成活动段检测后，采用滑动窗口法提取各手势对应的活动段信号的时域特征。滑动窗口法的原理如图7所示，即利用滑动窗对截取的活动段SEMG进行有效压缩，以用于后续的手势识别。图中：K表示滑动窗长度，H表示增量窗长度。

图7 滑动窗口法原理示意Fig.7 Schematic diagram of sliding window method

本文先随机选择滑动窗长度K=256 ms，增量窗长度H=128 ms进行时域特征提取，但识别结果并不理想。为了寻找更优的滑动窗，基于多个滑动窗进行时域特征提取实验。为避免康复机器人控制器出现延时，将滑动窗长度保持在300 ms以下［15］，并用隐含节点数为50的ELM分类模型（由于AFSA-ELM分类模型的时间成本较高，而ELM分类模型与AFSA-ELM的识别结果呈正相关且识别速度快，选用ELM可快速找到最优的滑动窗）进行手势识别，结果如表1所示，表中平均识别率为10次测试结果的平均值。

由表1可知，滑动窗的选取对手势识别结果的影响较大，识别准确率差值高达12.6%。根据所得结果，选择K=128 ms，H=64 ms的滑动窗为最优滑动窗进行特征提取。

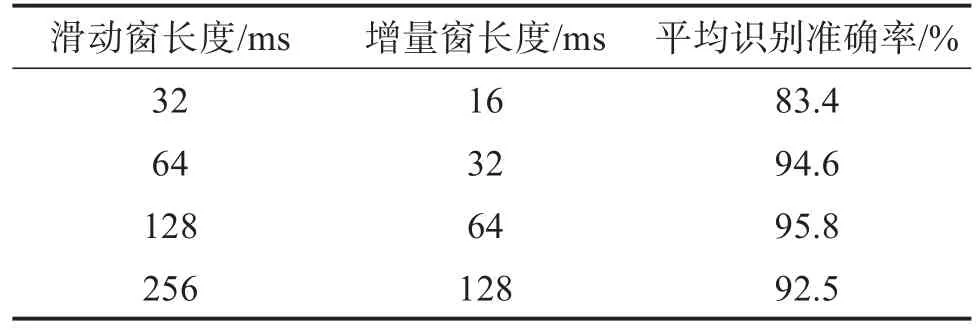
表1 基于不同滑动窗的手势识别准确率Table 1 Gesture recognition accuracy based on different sliding windows

3.3 最优特征组合与最优滑动窗验证

为了验证所选最优特征组合与最优滑动窗的优势，结合时域特征、样本熵和时域特征+样本熵（均经PCA降维处理）以及K=32 ms，H=16 ms的滑动窗，利用ELM分类模型对8种手势进行识别，并与基于K=128 ms，H=64 ms的最优滑动窗的识别结果进行比较。选用K=32 ms，H=16 ms的滑动窗进行对比的原因是表1结果显示基于该滑动窗的识别效果仅次于基于最优滑动窗的。基于不同特征和滑动窗的手势识别结果如表2所示。

表2 基于不同特征组合和滑动窗的手势识别结果Table 2 Gesture recognition results based on different feature combinations and sliding windows

从表2可以看出，当特征组合及滑动窗选择不理想时，手势的识别准确率是偏低的，而基于本文所选的最优特征组合与最优滑动窗的手势识别结果较为理想，对8种手势的识别准确率高达95.8%，充分说明了选择的合理性。由此说明，单一特征无法完全表征手势，而融合多个特征的特征组合可全面表征手势，但提取过多的特征会增加运算时间，因此有必要选择合适的特征组合。此外，选择合适的滑动窗也可进一步提升识别准确率。

4 AFSA-ELM分类模型的构建与结果分析

4.1 AFSA-ELM分类模型的构建与应用

根据上述方法，设人工鱼的数量n=10，最大迭代数D=5次，人工鱼视野V=100，移动步长S=2，利用AFSA对ELM的输入权值和隐含阈值进行寻优。当寻优次数达到所设的最大迭代数时，寻优终止并输出最优的输入权值和隐含阈值。需要注意的是，AFSA参数的选取对最终手势识别结果的影响较小，但人工鱼数量和迭代次数较大会导致寻优时间急剧增加，不利于运算。基于AFSA的ELM参数寻优迭代过程如图8所示。

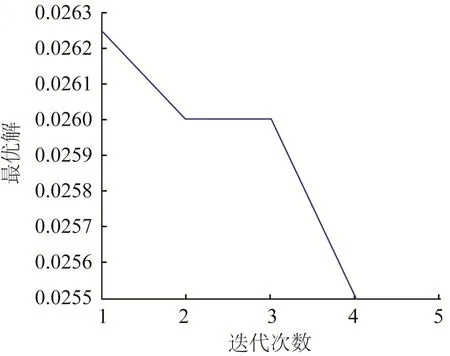
图8 基于AFSA的ELM参数寻优迭代过程Fig.8 Iterative process of ELM parameter optimization based on AFSA

基于建立的AFSA-ELM分类模型，取80%的SEMG作为训练数据，20%作为测试数据。将训练数据输入AFSA-ELM分类模型，以对该模型进行训练，而后将测试数据输入训练好的AFSA-ELM分类模型，以对8种手势进行识别，结果如图9所示，其中纵坐标中的1—8分别对应8种手势。由图9可知，AFSA-ELM分类模型对8种手势的识别准确率高达97.4%。

图9 8种手势的识别效果对比Fig.9 Comparison of recognition effect of eight gestures

4.2 不同分类模型的对比分析

为了验证所构建的AFSA-ELM分类模型的优势，分别与BP神经网络（输入层节点数为3，隐含层节点数为20，输出层节点数为8，传递函数为Sigmoid型）分类模型和未优化的ELM分类模型进行对比，结果如表3所示。表中识别准确率由10次测试结果的平均值与其标准差组成。

表3 基于不同分类模型的手势识别准确率对比Table 3 Comparison of gesture recognition accuracy based on different classification models %

由表3可知，AFSA-ELM分类模型对8种手势的识别准确率明显高于传统的BP神经网络分类模型，提高了3.5%；相比于未优化的ELM分类模型，提高了1.6%。这主要是因为BP神经网络易陷入过学习，导致整体识别结果不理想，而未优化的ELM由于参数的随机性大，使得识别稳定性较差。这充分说明了优化后ELM的输入权值和隐含阈值较优，使得识别结果得到了明显改善，由此验证了AFSA-ELM分类模型的精准性。

对于本文所研究的手势离线识别方法，除了考虑分类模型的识别效果外，训练和识别时间也是衡量分类模型优劣的重要指标。分类模型的训练和识别时间越短，表明其响应速度越快。对上述3种分类模型的训练和识别时间进行分析，结果如表4所示。其中AFSA的寻优时间未计入。

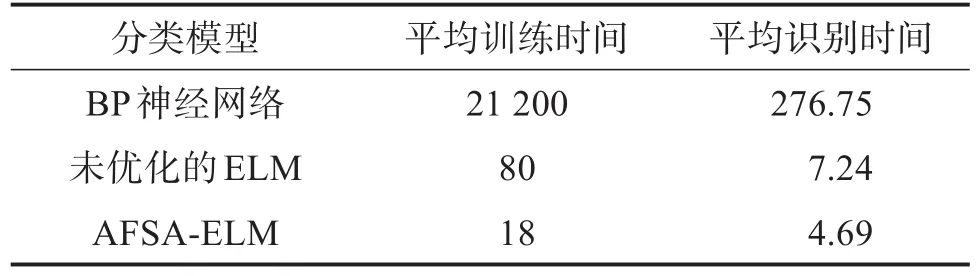
表4 不同分类模型的训练和识别时间对比Table 4 Comparison of training and recognition time of different classification models 单位：ms

由表4可知，BP神经网络分类模型的训练和识别时间远超过未优化的ELM分类模型，充分证明了ELM分类模型的有效性。在对比AFSA-ELM分类模型与ELM分类模型时，考虑到SEMG的特征数据量庞大，而AFSA寻优需要一定时间，故暂将寻优过程排除在外，直接选择AFSA优化好的ELM分类模型进行训练和识别。结果表明，AFSA-ELM分类模型的训练和识别时间较ELM分类模型分别少62 ms和2.55 ms。由于本文未考虑AFSA-ELM分类模型的寻优时间，其仅可用于对识别精度要求较高的离线分析，后续在实时、在线识别的应用上须作进一步改进。

5 结论

为了提高多手势的识别准确率，结合特征组合与滑动窗口法，提出了一种基于AFSA优化的ELM的多手势精准识别方法。结果表明，将样本熵引入时域特征组合并结合PCA降维处理时，ELM分类模型的识别准确率较高；搭配最优的滑动窗（滑动窗长度K=128 ms，增量窗长度H=64 ms）时，ELM分类模型的识别效果可进一步改善；所构建的AFSA-ELM分类模型对8种常用手势的识别准确率高达97.4%，优于BP神经网络和未优化的ELM分类模型。后续可将AFSA-ELM分类模型应用于机械运动控制、外骨骼控制等领域［16-17］。