不同层理页岩常规三轴压缩力学特性离散元模拟
2022-01-10杨圣奇孙博文田文岭
杨圣奇,孙博文,田文岭
1) 中国矿业大学深部岩土力学与地下工程国家重点实验室,徐州 221116 2) 中国矿业大学力学与土木工程学院,徐州 221116
随着对能源需求的增长,页岩气作为一种非常规清洁高效能源越发被人们关注. 我国页岩气技术可采储量位居世界第一,开发潜力广阔. 随着页岩气开采技术日益成熟,我国已经开始向埋深超过3500 m的深层页岩气资源进军. 页岩储层孔隙率、渗透率低,开采时常使用水平井水压致裂等方法来增加产气量,并且页岩在形成过程中会形成较多弱面,从而表现出不同程度的各向异性. 因此,进一步开展深部各向异性岩石力学特性的研究对深层页岩气开发具有重要指导意义.
长期以来国内外学者针对各向异岩石力学特征展开了一系列研究工作. 室内试验方面,文献[1-4]进行了层理页岩常规力学实验,分析了层理页岩抗压强度、破坏模式和波速的各项异性特征;熊健等[5-7]讨论了高温后及热力耦合作用对页岩物理力学特性的影响;何柏等[8]系统地分析了页岩体积变形规律,得到了页岩在压缩应力作用下的4个变形阶段;亓倩和朱维耀[9]通过建立两种分布渗透率分布模型结合稳态依次替换法,研究了页岩气储层中不稳定渗流压力扰动的传播规律;王辉等[10-12]对层状页岩开展了巴西劈裂试验,分析了页岩破坏模式、峰值强度与层理倾角的关系;Yang等[13]通过对龙马溪组页岩进行常规三轴试验分析了其各向异性特征,并根据应力-应变表征的能量关系提出了2种评定岩石脆性特征的新方法. 刁海燕[14]开展了泥页岩力学特性和脆性评价方面的研究,提出弹性参数与矿物成分组合法的新脆性评价方法;袁俊亮等[15]从页岩气储层岩石的脆性指数、断裂韧性、岩石力学特性3个方面,对页岩气储层可压裂性评价技术进行了研究,并建立了储层可压裂性立体分布图. 在数值模拟方面,郭天魁等[16]利用Abaqus有限元计算软件研究了地应力、井筒位置等对起裂应力的影响;卞康等[17]利用离散元软件研究了不同吸水时间下页岩的卸荷力学特性和破坏模式;梁正召等[18]使用RFPA2D模拟了由两种不同的岩石材料组成的不同岩层倾角的岩石试件的力学行为,对其单轴压缩下渐进破坏过程进行了研究;杨志等[19]使用RFPA2D研究了单轴压缩下不同均质度含不同方向层理面页岩的声发射特性,结果表明页岩层理面倾角和均质度对其峰值强度、破裂模式和声发射特性有显著影响. 综合前人研究可以看出,前人使用PFC研究不同层理页岩常规三轴宏微观力学特性及层理倾角对页岩脆性影响的成果相对较少,需要进行进一步研究.
因此,本文通过颗粒流程序模拟研究围压和层理倾角对页岩的力学特性影响. 首先基于“试错法[20]”获得一组可以反映室内试验[21]中β= 0°、90°(该角度为层理面与最大主应力间的夹角)页岩力学特性的细观参数,并通过破坏模式的对比做了进一步验证. 在此基础上对不同层理倾角页岩进行常规三轴压缩模拟,研究围压和层理倾角对页岩力学特性及破坏模式的影响,进一步加深对深部不同层理页岩的力学特性的了解,以期为相关工程提供一定参考价值.
1 数值模拟方法
PFC是常用于模拟岩土材料力学性能的离散元软件,在其二维模型中颗粒被视为单位厚度的刚性圆盘并通过颗粒的运动和相互作用来模拟材料的力学行为. 文献[22-24]在采用PFC模拟岩石材料时,表明颗粒间的接触模型选用平行黏结模型能够较好的反映岩石材料的力学特性,同时考虑到页岩的各向异性,通过安装光滑节理接触模型来模拟其层理面.
1.1 数值模型构建
本文对Yang等[21]完成的不同层理倾角页岩常规三轴压缩试验进行数值模拟研究. 试验中采用的页岩取自江西省庐山市,该页岩材料属于细晶结构,密度约为 2750 kg·m-3,孔隙率为 1.2%,主要矿物成分为白云母、石英、钠长石等. 以0°与90°两个角度对岩块进行钻取来获得尺寸为直径50 mm、高100 mm的圆柱体试样.
依据室内试验结果[21],在PFC中生成与室内试验尺寸相同的数值试样,直径50 mm、高100 mm.试样中颗粒最小半径为0.5 mm,最大与最小粒径比为1.66,且颗粒大小成均匀分布,颗粒密度为2750 kg·m-3. 为了模拟页岩层理特性,本文通过调用离散裂隙网络(DFN),采用高斯分布确定层理位置并安装光滑节理模型,从而构造出具有随机分布层理的数值模型,从形态上可以看出真实试样与数值模型一致,β=0°数值模型如图1所示. 基于上述参数,生成的模型中共含有12952个粒径均匀分布的颗粒,β= 0°和90°的模型试样分别含有30521、32325个接触,其中光滑节理接触的数量分别为4060、3009个. 该模拟采用位移控制的加载方式,上下两个墙的加载速度为0.05 m·s-1(PFC模拟中加载速率与室内试验中加载速率不同,0.05 m·s-1仍为准静态加载[25]). 其后根据室内试验标定出的细观参数建立层理倾角为15°、30°、45°、60°、75°页岩数值模型.

图1 β=0°页岩模拟试样示意图Fig.1 Numerical model of β=0° shale generated by PFC2D
1.2 细观参数标定
在细观参数标定过程中,首先生成不含层理面的试样,并利用“试错法”对其参数进行校准,过程如下:先对线性接触模量进行反复试验使得数值模型的弹性模量与室内实验结果相近,然后保持接触模量不变对刚度比进行修改来获取与实际试验接近的泊松比,最后对黏结比进行调整从而改变其峰值强度包络线的斜率,黏结比即法向黏结强度与切向黏结强度之比. 获取不含层理面数值模型的参数后,其后在模型中加入光滑节理模型,同样用“试错法”来校准其细观参数,经过对细观参数的反复修改,使得数值模拟宏观力学行为与室内试验的结果相接近. 标定所得的细观参数如表1所列.

表1 页岩PFC2D细观参数Table 1 Micro-parameters of shale in PFC2D
表1中,pb_emod为平行黏结接触模量,pb_krat为平行黏结刚度比,pb_ten为平行黏结法向黏结强度,pb_coh为平行黏结切向黏结强度,sj_kn为光滑节理法向刚度,sj_ks为光滑节理切向刚度,sj_ten为光滑节理抗拉强度,sj_coh为光滑节理黏聚力. 为了验证上述细观参数的合理性,本文使用表1中细观参数对β=0°和90°的页岩进行常规三轴压缩模拟验证. 图2给出的是数值模型与室内试验的峰值强度(σs)随围压变化的对比图. 由图 2(a)可知,当β=0°时,试验和模拟峰值强度最大相差 43.3 MPa(围压σ3=5 MPa),相对误差为21.65%,并且围压为5 MPa时的室内试验峰值强度明显较回归直线大,其余围压下实验结果和模拟结果差距很小. 由图 2(b)可知,当β=90°时,从图中可以观察到两者的结果十分相近,两者最大相差 14.8 MPa (σ3=20 MPa),相对误差为 6.42%. 通过线性拟合结果可知,试验结果和模拟结果均遵循摩尔-库伦强度准则,且数值模拟所得结果较实验结果相差较小,说明选用的细观参数合理.
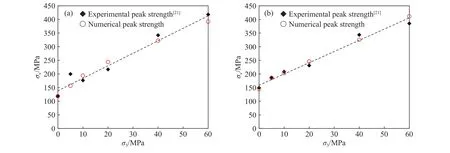
图2 层理页岩室内试验与模拟峰值强度对比. (a)β=0°;(b)β=90°Fig.2 Comparison between the experimental and numerical peak strength of the bedding shale: (a) β = 0°; (b) β = 90°
为了更好的验证表1中数值模型细观参数的合理性,将β= 0°和90°页岩的室内试验与模拟所得的破坏模式进行了对比,如表2所示. 页岩的破坏模式不仅受层理面倾角的影响,同时随着围压的改变试样最终破坏模式也随之改变. 当β=0°时,在模拟结果中页岩在单轴压缩下的破坏模式为沿多个层理面的劈裂破坏,除此以外还出现了部分贯通层理面的剪切裂纹,这与试验结果中试样出现以沿层理产生的拉裂纹为主并且最终呈现劈裂破坏的形式十分相似;随着围压的增加,模拟和试验结果均出现“V”形剪切破坏,并且模拟结果中的裂纹数目也随之增加,此时试验与模拟破裂模式存在差异,这是由于高围压的限制作用增强了试样的承载能力,试样需要产生更多的裂纹才会使试样失去承载能力,而且模拟中使用的刚性墙体施加围压一定程度上减少了在纵向不均匀性的影响. 当β=90°时,页岩在单轴压缩情况下,破坏时出现贯穿层理面的劈裂裂纹和沿层理面产生的横向剪切裂纹;施加围压后,数值模拟结果与试验结果均表现为贯穿多层理的剪切破坏,但在试验结果中多表现为单一剪切破坏,在模拟结果中表现为共轭剪切破坏.
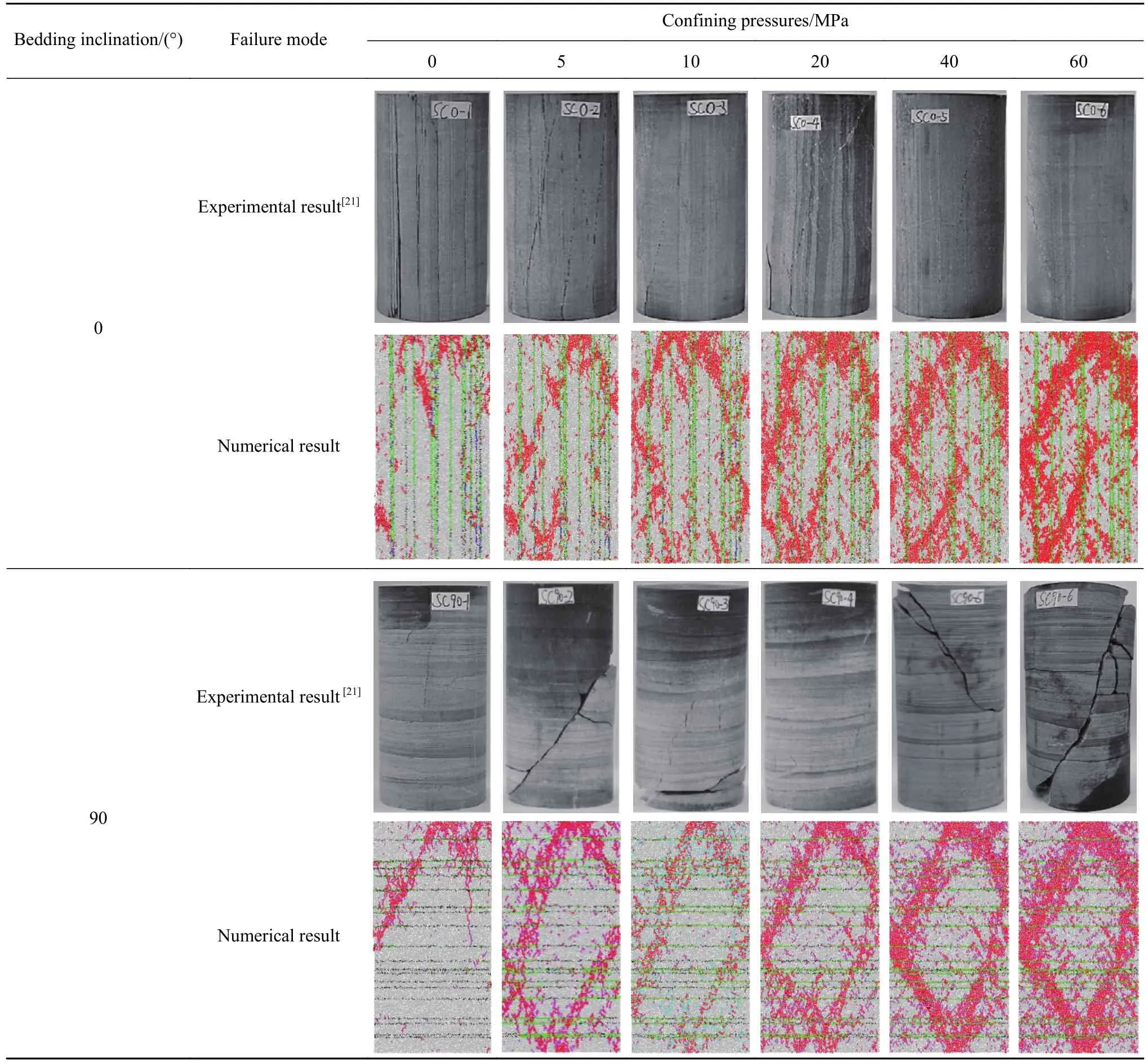
表2 常规三轴压缩下层理页岩试验与模拟破坏模式对比Table 2 Comparison between experimental and numerical failure modes of the bedding shale specimens underconventional triaxial compression
通过对模拟与实验结果中的峰值强度及破坏模式的对比可以看出,使用该组参数PFC可以较好地模拟β= 0°和90°的页岩的力学特性. 在此基础上可以使用PFC2D对不同层理角度页岩进行常规三轴压缩模拟,分析围压及层理角度对页岩力学特性的影响.
2 数值模拟结果分析
为了分析层理倾角和围压对页岩力学特征的影响,使用上述标定过的模型细观参数建立β=15°、30°、45°、60°和 75°的数值模型,并对其进行不同围压作用下的常规三轴模拟,围压设定为0、5、10、20、40和 60 MPa. 根据数值模拟结果对含不同层理倾角页岩试样峰值强度及破坏模式等进行分析.
2.1 不同层理页岩峰值强度的分析
图3(a)为不同围压下峰值强度随层理倾角的变化曲线,从图中可知峰值强度随着层理倾角的增加总体呈“U”形变化,即峰值强度随倾角增加先减小后增大,同时可以观察到在β=90°时峰值强度达到最大值,当β=30°、45°时峰值强度最小. 不同围压下页岩试样峰值强度随层理倾角增加的变化趋势有所区别,在低围压情况下,β从0°增至30°的过程中峰值强度的下降趋势逐渐变缓;从30°增加到90°时峰值应力的增长曲线相对平缓.而在高围压(σ3=40 和60 MPa),峰值强度曲线逐渐变陡;β从30°增加至90°的过程中,峰值强度曲线的变化趋势是由缓变陡再变缓的过程. 该规律符合结构面的强度效应[26],即β1=π/4+φ/2(β1为层理面的法线方向与最大主应力间的夹角,φ为内摩擦角)时,试样强度最小.

图3 页岩峰值强度参数与层理倾角的关系. (a)峰值强度随层理倾角的变化;(b)黏聚力、摩擦角随层理倾角的变化Fig.3 Relationship between the peak strength parameters of shale and bedding inclinations: (a) peak strength variation vs bedding inclinations; (b)cohesion variation C and internal friction angle φ vs bedding inclinations
由图3(b)可以观察到在模拟结果中试样的黏聚力随层理面倾角的增大同样呈“U”形变化趋势黏聚力可视为剪切面无正应力时的抗剪强度. 另一方面摩擦角φ随层理面倾角的增大呈非线性变化,β从 0°增大到 15°时,φ由 39.14°增大到 43.6°;当β从 15°增大到 45°时,φ则从 43.6°减小到 30.47°,当β由 60°增至 90°时,φ=37.75°~38.38°,这说明β为60°~90°时,层理面倾角对内摩擦角影响不大. 该数值模拟结果同Yang等[13]、王洪建等[27]的研究结果相似.
2.2 破坏模式分析
图4~8为不同层理倾角页岩在不同围压下的破坏模式. 在试样加载初期,层理倾角为0°~75°的页岩试样的初始裂纹均从层理位置处起裂,继而在基质中产生裂纹,并逐渐形成贯通层理的宏观裂纹,同时从模拟结果可以观察到随着围压的升高试样破坏时组成宏观裂纹的微裂纹数目显著增加,但由于层理倾角和围压大小不同对试样最终的破裂模式的影响也不尽相同. 从图4~8可见,单轴情况下,β=15°和45°页岩微裂纹沿层理面发育,使得试样发生沿层理面的剪切破坏,层理倾角为60°和75°试样呈现出贯穿层理的劈裂破坏.

图4 不同围压层理页岩最终破裂模式 (β=15°)Fig.4 Ultimate failure modes of the bedding shale in different confining pressures (β=15°)

图5 不同围压层理页岩最终破裂模式 (β = 30°)Fig.5 Ultimate failure modes of the bedding shale in different confining pressures (β = 30°)

图6 不同围压层理页岩最终破裂模式 (β = 45°)Fig.6 Ultimate failure modes of the bedding shale in different confining pressures (β = 45°)
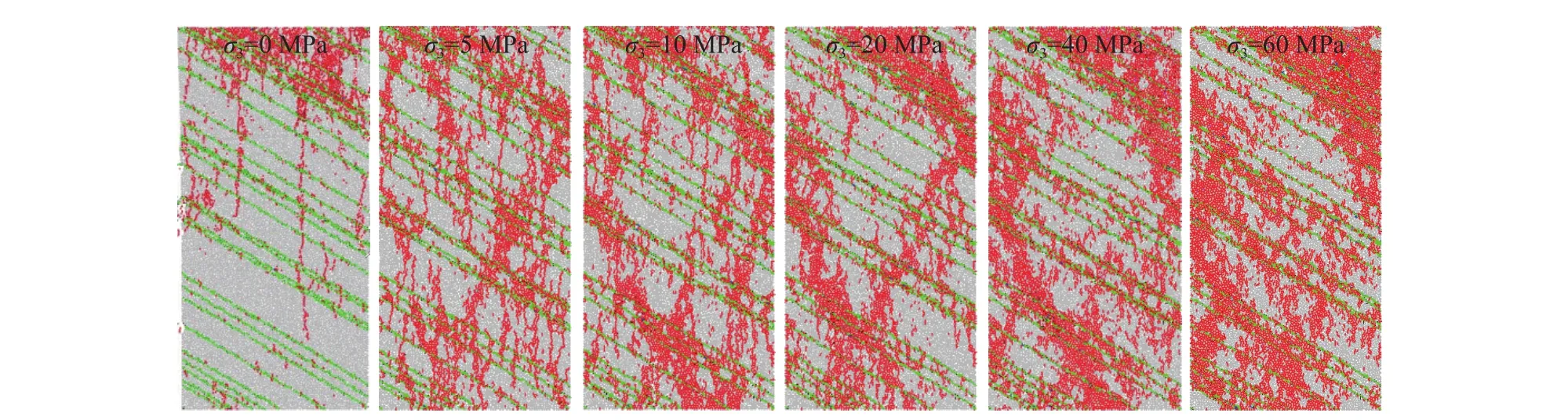
图7 不同围压层理页岩最终破裂模式(β=60°)Fig.7 Ultimate failure modes of the bedding shale in different confining pressures (β = 60°)

图8 不同围压层理页岩最终破裂模式(β = 75°)Fig.8 Ultimate failure modes of the bedding shale in different confining pressures (β = 75°)
当β=15°时,随着围压的增加,试样出现的贯穿层理面的剪切裂纹,呈现出共轭剪切破坏模式.当β=30°时,σ3=5和 10 MPa情况下的破裂模式为沿层理面的剪切破坏;当围压增大至20 MPa时,试样表面存在多条沿层理面的剪切裂纹,同时还产生了部分贯穿层理面的剪切裂纹;随着围压的继续增加,破坏模式表现为沿层理面的剪切破坏.当β=45°,围压在5~40 MPa时,试样沿着层理面产生滑移,形成贯穿试样的剪切破坏,且在端部出现部分拉伸裂纹;而当围压增到60 MPa时,其破坏模式为贯穿多层理面的剪切破坏.β=60°和75°试样在围压作用下破坏时表面有多条沿层理的剪切裂纹和贯通层理面的“V”形剪切裂纹,形成共轭剪切破坏. 从上述分析可以看出,破坏类型主要分为两类:β=30°和45°试样以沿层理面的剪切破坏为主,其余角度试样多发共轭剪切破坏.
2.3 试样破坏的位移场分析
在压力作用下试样内部颗粒会产生相对位移,这一变化会使颗粒间的黏结发生断裂,裂纹的演化过程实际就是颗粒间相对位移不断产生的过程. 为了研究不同层理页岩试样破坏后的位移场,选取β=15°、45°、75°在单轴压缩下破坏试样中裂纹附近的位移场进行分析,如图9所示. 图中小箭头颜色代表着位移的大小,大箭头表示裂纹附近颗粒的运动方向,黑色直线为层理所在位置.

图9 不同层理倾角试样位移场示意图. (a)β=15°;(b)β=45°;(c)β=75°Fig.9 Diagram of the displacement field of specimens with different bedding inclinations: (a) β=15°; (b) β=45°; (c) β=75°
图9(a)为β=15°试样在单轴压缩作用破坏下的局部位移矢量图,从图中可得颗粒间沿层理方向的位移差是试样沿层理发生剪切破坏的主要原因;图 9(b)为β=45°试样局部位移矢量图,图中沿层理剪切的裂纹是由沿层理方向的位移分量方向相反产生的,同时图中拉伸裂纹的出现是由周围颗粒发生反向位移造成的;图9(c)为β=75°试样破坏后的局部位移矢量图,此时试样中的裂纹是由于颗粒的横向位移差产生,由于层理与轴向应力的夹角较大,此时层理对试样整体力学特性的影响较小. 由此可知在层理与轴向应力夹角较小时,层理对其周围颗粒的运动方向及大小影响较为明显,颗粒容易发生沿层理方向的相对位移从而宏观上表现出沿层理面的剪切破坏. 这是由于层理面为页岩的弱面,单轴情况下,层理面所承受的剪切应力和张力相对较大,当层理面所承受应力大于其强度,试样沿层理面发生滑移破坏. 另一方面当层理面与轴向应力夹角较大时,层理面未表现明显弱面效应,在基质中产生劈裂破坏,此时试样破坏需要较大的不连续横向位移.
2.4 微裂纹数目演化规律
试样的损伤破裂是其微裂纹的萌生、扩展、贯通的宏观体现. PFC可以记录试样加载过程中微裂纹的数目变化,据此可以定量分析三轴压缩下不同层理倾角和围压作用下页岩的损伤过程. 由于同一层理倾角在不同围压下的演化趋势大致相同,此处选取一个倾角的模拟结果进行分析. 图10(a)为β= 0°试样在不同围压作用下微裂纹演化曲线,从图中可见,随着轴向应变的增大,微裂纹数目的演化规律大致可以分为缓慢增长阶段、快速增加阶段和趋于稳定阶段,且不同围压作用下微裂纹数目的演化规律大致相同. 随着围压的升高,微裂纹快速增加阶段的起始点对应的轴向应变和试样最终破坏时产生的裂纹数目均有所增加. 高围压情况下,在微裂纹快速增加阶段产生相同轴向应变时裂纹增长的速率更小,这说明围压可以有效的抑制微裂纹的产生从而提高试样承载能力.

图10 层理页岩微裂纹演化曲线. (a)不同围压下β=0°页岩微裂纹演化规律;(b)不同层理倾角页岩微裂纹演化规律(σ3=60 MPa)Fig.10 Evolution curves of the number of microcracks of the bedding shale: (a) evolution law of shale microcrack at β=0° under different confining pressures; (b) evolution law of microcracks in shale with different bedded inclination angles (σ3=60 MPa)
图10(b)给出了在高围压 (σ3=60 MPa)作用下,不同层理倾角页岩微裂纹数目随轴向应变的演化情况. 由图 10(b)可知,当β=0°和 90°时,微裂纹数目的演化趋势较为相似,即先缓慢增加,接着快速增加,最后逐渐趋于稳定.β=15°~75°试样微裂纹数目在加载初期快速萌生,随着轴向应变的继续增加,微裂纹数目的增长速率变缓,最后微裂纹数目逐渐趋于稳定状态. 出现这种现象主要是因为当β=15°~75°时,在加载初期首先在试样的层理位置开始萌生剪切裂纹,此阶段裂纹数目增长较快;随着轴向应力的增加,内部应力重新分布,同时围压限制了试样沿层理面的滑移作用,裂纹开始在基质中产生,微裂纹数目稳步增长,但此时裂纹产生的速度比在层理中产生的要慢;最终形成沿层理面或贯穿层理面的剪切破坏. 而β=0°和90°试样在围压的作用下的侧向变形受到抑制,层理面上剪切作用和张力较小,故加载前期未出现微裂纹快速增加的现象. 虽然不同层理倾角页岩微裂纹数目的演化规律略有不同,但最终破坏试样的微裂纹总数先降低后升高.
3 脆性评价
脆性是岩石材料的一项重要性质,在页岩气的开采中常使用水压致裂来丰富裂隙网络,从而提高页岩气产量,而页岩的脆性对水压致裂裂纹形成产生较大影响. 现有脆性评价的方法较多,包括基于矿物成分的评价方法、应力应变曲线的评价方法、统计损伤本构关系的评级方法、岩石力学参数的评价方法、岩石破裂角度的评价方法和岩石硬度及断裂韧度的评价方法等[28]. 通过对上述评价方法的分析,本文拟采用应力应变曲线表征的能量关系来评价岩石的脆性,即峰值应力处的理想弹性能与峰前总能量之比,见式(1)[13]. 理想弹性能Uei及峰前总能量Ue+Up所表示的面积如图11所示.

图11 峰前应力-应变曲线法Fig.11 Method of stress-strain curve before peak
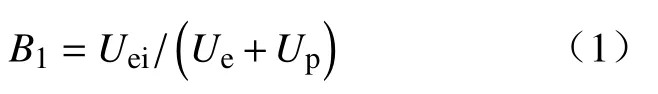
式中,B1代表脆性指数,Uei代表理想弹性能,Ue为弹性能,Up为耗散能.
结合上述对脆性指标定义,可见当脆性指数B1越大岩石的脆性越强. 由于数值模拟在进行三轴压缩试验时不会出现压密阶段,故此处所得脆性指数B1要小于室内试验所得. 图12为不同层理页岩脆性指数与围压关系,从图中可见不同层理倾角试样脆性指数的变化受围压影响较为一致,即随着围压的增加试样脆性指数整体呈下降趋势,这说明围压的作用可以抑制岩石脆性的表达. 图13为相同围压作用下页岩脆性指数与层理倾角关系,从图中观察到,脆性指数在相同围压作用下随着层理倾角的增大变化趋势并不一致,在低围压情况下脆性指数呈现两头高中间低的趋势;高围压情况下呈波动形变化. 这可以通过岩石破坏形式来解释,低围压时脆性指数中间低是因为此时试样破坏模式呈现剪切破坏,试样在剪切面产生滑移的过程中会耗散掉一部分能量,而劈裂破坏时能量会释放的更快,因此表现为两头高中间低的趋势. 同时由上文可知,此时试样发生剪切破坏的微裂纹总数较少,即破裂面发育不充分,脆性较低;而高围压时(σ3=60 MPa),围压的影响大于层理倾角的影响,故未表现出明显规律[29].

图12 不同层理倾角下脆性指标随围压的变化Fig.12 Variation of brittleness index with confining pressure under different bedding dip angles

图13 不同围压下脆性指标随层理倾角的变化Fig.13 Variation of brittleness index with bedding dip under different confining pressures
4 结论
(1)β为 0°和 90°页岩常规三轴模拟结果与实验结果吻合较好. 页岩峰值强度、黏聚力随着层理倾角的增加呈“U”形变化,且在β=30°或 45°时强度最低;内摩擦角随着层理倾角的变化呈非线性变化.
(2)层理的弱面效应随之与轴向应力夹角增大而弱化,在位移场中表现为层理倾角对其周围颗粒的位移方向及大小的影响随着倾角与轴向应力的夹角的增大而减小.
(3)在同一层理倾角下,随着围压的升高,微裂纹快速增加阶段的起始点对应的轴向应变和试样最终破坏后产生的裂纹数目有所增加. 在同一围压下,随着层理倾角的增加,试样最终破坏时产生的微裂纹数目先减少后增多.
(4)同一层理页岩的脆性随围压的增加整体呈下降趋势. 在低围压下,页岩脆性随层理倾角的增长呈两头大中间小的变化趋势,在高围压下,页岩脆性随层理倾角变化未表现出明显规律.
