锂离子电池电极中多级孔道结构设计

汪宇，张禹，童微雯，叶光华，周兴贵，袁渭康

（1华东理工大学化学工程联合国家重点实验室，上海 200237；2上海空间推进研究所，上海 201112）

引 言

锂离子电池具有能量密度高、功率密度大以及循环寿命长等特点，已经成为便携式电子产品中最受欢迎的储能设备。然而，近年来为了满足驱动电动汽车的需求，锂离子电池在能量密度和功率密度方面仍需要进一步提高[1-4]。为了达到这一目的，研究者做了大量工作，这些工作主要包括开发新的电极材料和在不改变材料组成的情况下设计电极孔结构[5-8]。虽然后一种方法得到的关注相对较少，但它也可以在很大程度上改善锂电池的性能。

锂离子电池在充放电过程中，锂离子从一个电极转移到另一个电极，该迁移过程是决定其电池性能的关键之一[9]。在较高的充放电倍率下，锂离子较强的扩散阻力会引起严重的浓差极化，导致容量衰减，进而降低电池的能量密度和功率密度。这种扩散阻力主要来自于多孔电极，狭窄曲折的孔道会极大地阻碍锂离子的扩散[7,10]。因此，需要设计优化锂离子电池电极的孔道结构，以提高电池的充放电性能。

一些工作已经研究了电极的孔道结构对锂离子电池性能的影响[11-19]。例如，Fuller等[14]和Newman等[18]发现，高孔隙率的薄电极在较高的放电倍率下仍具有较小的扩散限制，但孔隙率较低的厚电极在低放电倍率下性能更好，因为较低的孔隙率意味着活性材料体积分数更大。Ramadesigan等[19]和Golmon等[13]研究报道，改变电极中孔隙率的空间分布可以降低锂离子的扩散阻力，从而提高放电容量。然而，Dai等[11]的研究表明，只有平均孔隙率远离最优值时，电极孔隙率的空间分布才可以提高电极性能。以上研究表明，通过设计孔道结构可以在一定程度上提高电极的性能。

在设计沸石等多相催化剂的孔道结构时，采用多级孔道结构是改善催化剂性能的有效途径[20-22]。大孔有利于分子的快速扩散，而微孔为反应提供了较大的内表面积。由于锂离子电池电极和非均相催化剂都存在扩散限制的问题，这种利用多级孔道的方法也可以有效地改善锂离子电池的性能。

部分研究者已经在实验中制备了含多级孔道的锂离子电池电极，其中包括在普通电极中引入垂直于集流体的低曲折因子孔道，作为锂离子传输的“高速公路”（图1）。例如，Bae等[7,23-24]利用共挤出、磁模板以及冷冻铸造等方法制备了具有这种多级孔道结构的LiCoO2和LiNi0.8Co0.15 Al0.05 O2正极，结果表明在较高的充放电速率下，这种具有多级孔道结构电极的比容量要比相应的传统电极高几倍。Billaud等[8]利用外磁场制备了具有多级孔道结构的石墨负极，在2C的放电倍率下，这种负极的锂存储容量比传统方法制备的负极高3倍。这些实验结果表明，含垂直于集流体的低曲折因子孔道的锂离子电池电极比传统电极更具优势。为了获得最优的锂离子电池电极的多级孔道结构，需要建立合理的数学模型。Ye等[25]通过数值模拟和理论分析，推导出了孔道结构与曲折因子之间关系的表达式。然而，截至目前，很少有文献报道上述多级孔道结构的数值模拟和优化。

图1 多级孔电极的结构示意图(a)；三维结构到二维重复单元的简化(b)；以钴酸锂多级孔电极为正极和锂金属为负极的半电池的二维结构示意图(c)Fig.1 A schematic of the electrode with the hierarchical pore network(a);Simplification of a three-dimensional repeating unit into a two-dimensional one(b);A two-dimensional schematic of the half-cell with the hierarchically structured electrode as LiCoO2the cathode and the lithium metal as the anode(c)

本工作基于Newman模型[26-27]，建立了一种能描述锂离子电池电极中多级孔道结构的二维模型。由于钴酸锂电极广泛应用于电动汽车当中[28-29]，这里将其作为模型电极。在普通钴酸锂电极中引入垂直于集流体的低曲折因子孔道，并优化这些低曲折因子孔道的直径和孔隙率，以获得较高的能量密度和功率密度。此外，本工作还研究了电极的总孔隙率和厚度对低曲折因子孔道优化结果的影响。

1 建 模

1.1 多级孔电极

图1(a)显示本工作中多级孔电极的典型三维结构，其中电极活性材料为钴酸锂。垂直于集流体的圆柱孔道被引入到电极涂层当中，这些低曲折因子（即τ=1）的孔道是锂离子传输的“高速公路”，钴酸锂颗粒间曲折狭窄的孔道不利于锂离子的传输，但为电化学反应提供了较大的内表面积。由于对该三维电极进行数值模拟时，计算量较大，本工作对该电极的三维结构进行了简化，并选取一重复单元进行数值模拟。本文假设圆柱孔道在电极涂层上呈现错列式排布，因此该三维电极的最小重复单元为中心有圆柱形孔的正六边棱柱[图1(b)]。采用Bae等[7]提出的方法将该三维重复单元简化为二维重复单元，以节省计算成本。Bae等[7]将正六边棱柱等效为具有相同横截面积的圆柱体，然后将该圆柱体简化为长方形二维结构，并证实了该简化方法的可靠性。为了分析并优化这种多级孔电极的性能，模拟了以钴酸锂电极为正极、金属锂为负极的半电池放电过程。该半电池的结构如图1(c)所示，其中电极厚度为h，低曲折因子孔道直径为d，相邻两个孔的间距为D。模拟中采用了半电池的一个重复单元，并采用周期性边界条件。

1.2 模型方程

1.2.1 电荷守恒 在多级孔电极内，电流的传输有两条途径，锂离子在电解液中的输运和电子在固体材料上的传输，充放电过程中总的电流密度(I)可通过式(1)计算：

式中，il为锂离子在电解液中传输带来的电流密度，A/m2；is为电子在固相材料间传输时带来的电流密度，A/m2。is可通过欧姆定律来计算：

式中，σ为固相材料的电导率，S/m；ϕs为固相材料上的电势，V。il可根据式（3）[13-14]计算：

式中，κeff为电解液的电导率，S/m；ϕl为电解液中的电势,V；f为电解液中的活度系数为锂离子在电解液中的迁移数[30]；cl为电解液中电解质浓度，mol/m3；R为理想气体常数，J/(mol·K)；F为法拉第常数，C/mol；T为温度，K。式(2)和式(3)的边界条件如下：

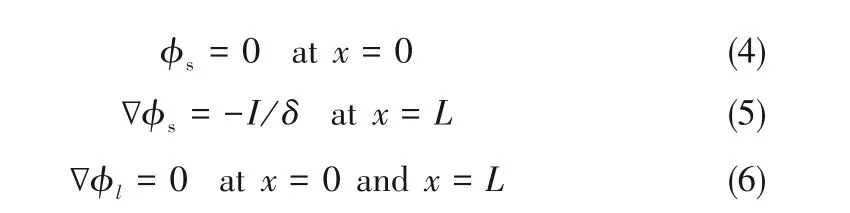
1.2.2 物料守恒 锂离子在电极活性材料颗粒中的嵌入与脱嵌过程可用Fick定律来描述，本文假设电极材料颗粒为球形，并且具有相同的直径，此时活性材料颗粒中锂离子的物料守恒方程为：

式中，Ds为锂离子在电极活性材料内的扩散系数，m2/s；r为活性材料颗粒所处的半径位置，m;cs为锂离子在r处的浓度，mol/m3;t为时间,s。式(7)的边界条件为：

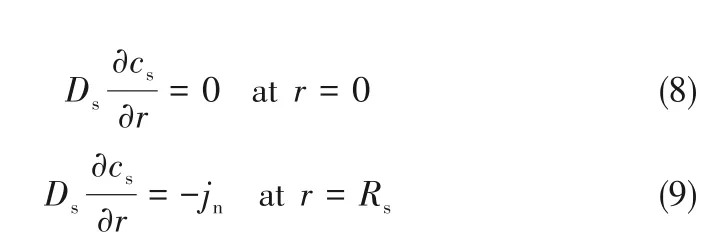
其中，Rs为电极活性材料颗粒的半径，m;jn为锂离子在活性材料外表面的通量,m2/s。

锂离子在电解液中的扩散可通过浓溶液理论来描述，其物料守恒方程为：

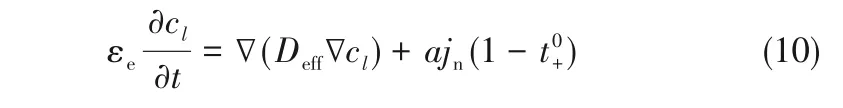
式中，εe为电极单元的孔隙率；a为电极单元的比表面积，m2/g;Deff为电极单元中锂离子的有效扩散系数,m2/s。Deff可通过式(11)计算获得：

式中，Dl为电解液中锂离子的扩散系数，m2/s；m为Bruggeman因子，可参考文献值进行设置[30]。式(10)的边界条件如式(12)：

1.2.3 电化学动力学 电极活性材料和电解液界面上会发生电荷转移过程，该过程可采用Butler-Volmer方程来描述：

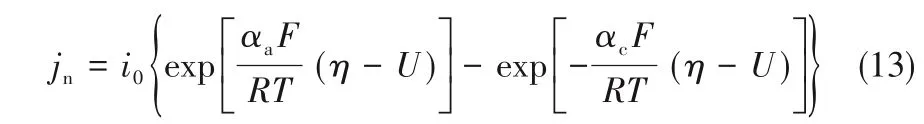
式中，i0为交换电流密度，A/m2；αa和αc分别为阳极和阴极的电荷转移系数；η为表面过电势；U为开路电压。i0可采用式(14)[31]计算：

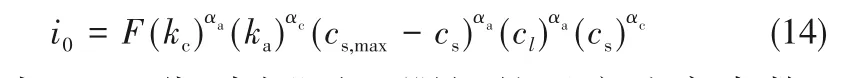
式中，ka、kc分别为阳极、阴极的反应速率常数；cs,max-cs为电极活性材料颗粒表面锂离子的空位浓度，mol/m3。η被定义为：

1.3 模拟与优化

利用COMSOL Multiphysics软件对上述建立的二维模型进行求解，采用有限元法对计算区域进行网格划分，其中网格数足够多(＞5000)，以获得准确的模拟结果。模型计算时所用的参数列于表1，此外开路电压的表达式参照Doyle等[32]的工作。模拟后可得到放电电压随时间变化的曲线，对该曲线进行积分计算，便得到电池的能量密度(SE)和功率密度(SP)：

表1 本工作数值模拟中所用到的参数Table1 Parameters for the numerical simulations in this work

式中，V为半电池的体积，m3。

本工作分别优化了多级孔道中低曲折因子孔道的直径(d)和孔隙率(d2/D2)，以获得最大的能量密度。另外，本工作还讨论了电极的总孔隙率(εt)和电池的厚度(h)对上述优化结果的影响。将低曲折因子孔道引入电极中时，假设电极总孔隙率保持不变，总孔隙率(εt)和电极柱中孔隙率(εe)之间的关系可通过式(18)描述：

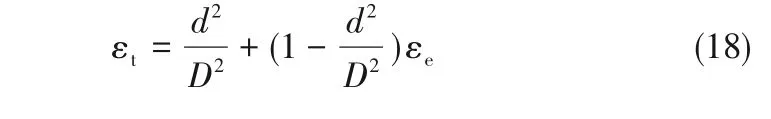
2 结果与讨论

2.1 典型结果对比

本工作首先比较了多级孔电极和普通电极，以说明多级孔电极的优异性能。多级孔电极和普通电极保持相同的总孔隙率(0.36)和厚度(200μm)，以消除这些因素对两种电极比较结果的影响。图2给出了两种电极对应半电池在不同放电倍率下的放电特性曲线、Ragone图（功率密度-能量密度图）和典型的锂离子浓度分布图。放电速率较低(≤0.5 C)时，Li+的扩散限制较弱，在这种情况下，二者的电压均呈现缓慢下降趋势，且它们容量衰减也都较小[图2(a)、(b)]，此时二者的能量密度非常接近[图2(c)]。而当放电速率较高(≥1C)时，Li+的扩散限制很强，与普通电极相比，多级孔电极对应的电势下降速度较慢，容量损失较小[图2(a)、(b)]，因此，多级孔电极对应的能量密度也高于普通电极对应的能量密度[图2(c)]。例如，在2C时，多级孔电极对应的能量密度为404Wh/L，而普通电极对应的能量密度仅为279Wh/L。低曲折因子孔道在Li+扩散过程中起到了“高速公路”的作用，它显著减弱了扩散限制，这一点可以从多级孔电极和普通电极中Li+浓度梯度的差异得到证明[图2(d)]。为了使多级孔电极的性能最大化，需要进一步优化多级孔道结构，这些优化将在下文中介绍。

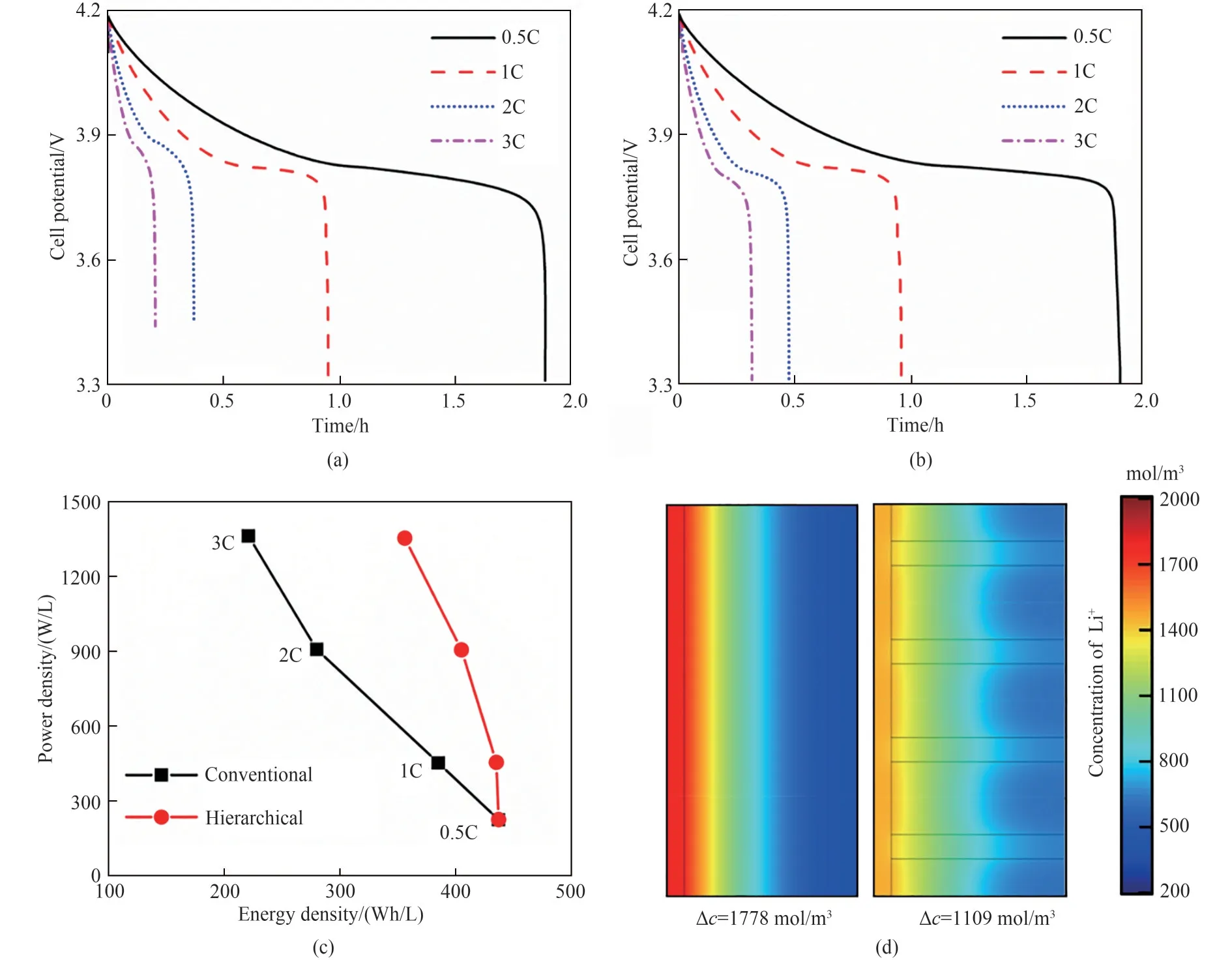
图2 普通电极(a)和多级孔电极(b)对应的半电池在0.5 C、1C、2C和3C放电倍率下的放电特性曲线；由图2 (a)、(b)计算得到的Ragone图(c)；当放电倍率为2C时，普通电极和多级孔电极在放电120s时的Li+浓度分布图(d)（模型参数：电池厚度h=200μm，总孔隙率εt=0.36 ，低曲折因子孔道的直径d=20μm，低曲折因子孔道所占的孔隙率d2/D2=0.0625 ，其他参数见表1）Fig.2 Time-dependent cell potentials under the discharge rates of0.5 C,1C,2C and3C for a conventional electrode(a)and a hierarchically structured electrode(b);The Ragone plots obtained from Figs.2(a)and2(b)(c);Typical concentration profiles of Li+at t=120s under the discharge rate of2C for the conventional electrode and the hierarchically structured electrode(d)(Simulation parameters:h=200μm,εt=0.36 ,d=20μm,and d2/D2=0.062 5.The other parameters are given in Table1)

2.2 多级孔电极孔隙率的优化

图3为普通电极和具有不同低曲折因子孔道孔隙率(d2/D2)多级孔电极对应的Ragone图，其中d2/D2变化范围为0.04 ～0.25 。图3(a)中，多级孔电极中低曲折因子孔道的直径(d)固定为30μm。当放电速率小于1C时，不同d2/D2对应的能量密度非常接近，而当放电速率大于1C时，能量密度随d2/D2的增加而增大。例如，在放电倍率为3C时，d2/D2=0.04 、0.09 、0.16 和0.25 对应的能量密度分别为328、370、408和421Wh/L，比普通电极(220Wh/L)的能量密度分别提高了49.1%、68.2%、85.4%和91.4%，见表2。此外，当d2/D2=0.25 时，随着放电倍率的逐渐升高，功率密度从93W/L增加到1367W/L时，能量密度损失小于17Wh/L，说明此时多级孔电极的性能较优。当放电倍率小于1C时，Li+受到的扩散限制很弱，此时改变d2/D2只能较小地改变能量密度，这也解释了图3(a)中较为接近的能量密度。此外，在图5～图7中也可以观察到类似的结果，这些结果也可以用同样的方式来解释。d2/D2越大，表明电极中低曲折因子孔道数量越多，电极柱越窄，越利于Li+的扩散。因此，在图3(a)中，拥有较大d2/D2的多级孔电极的性能较好，尤其是在高放电速率下性能更为优异。

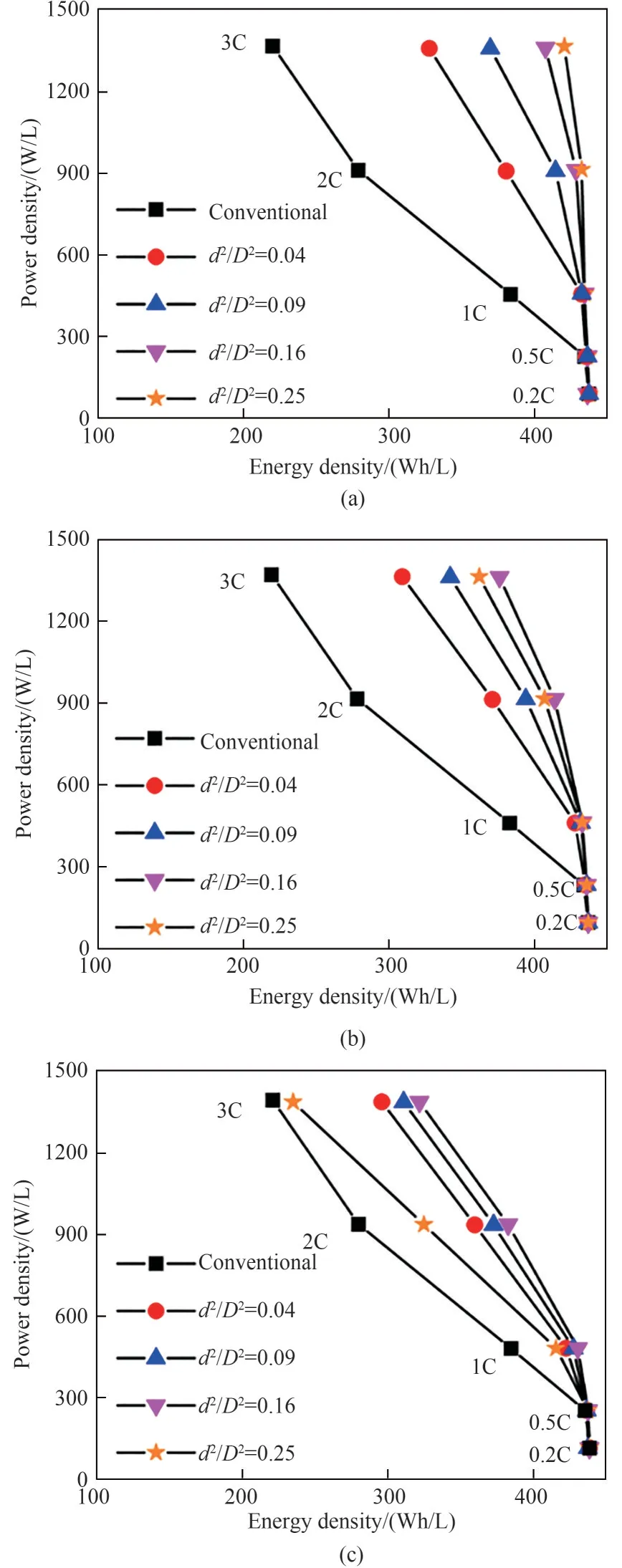
图3 普通电极与具有不同低曲折因子孔道孔隙率（d2/D2=0.04 、0.09 、0.16 和0.25 ）多级孔电极对应的Ragone图：(a)d=30μm；(b)d=60μm；(c)d=90μm(模型参数：h=200μm，εt=0.36，其他参数列于表1)Fig.3 Ragone plots for the conventional electrode and the hierarchically structured electrodes with d2/D2=0.04 ,0.09 ,0.16 ,and 0.2 5.(a)d=30μm;(b)d=60μm;(c)d=90μm(Simulation parameters:h=200μm,εt=0.3 6.The other parameters are given in Table1)

在图3(b)中，多级孔电极中低曲折因子孔道直径固定为60μm。在这种情况下，当d2/D2从0.04 增加到0.16 时，能量密度也随之增加，而当进一步增加d2/D2到0.25 时，能量密度反而降低了。因此，当低曲折因子孔道直径为60μm时，d2/D2=0.16 是最优的，此时在3C处的最大能量密度为377Wh/L，比普通电极(220Wh/L)高71.4%，见表2。在图3(c)中，多级孔电极中的低曲折因子孔道直径固定为90μm。此时，当d2/D2从0.16 增加到0.25 时，能量密度出现了明显的下降，因此最优的d2/D2为0.16 ，它在3C处的最大能量密度为321Wh/L，比普通电极大45.9%，见表2。d2/D2越大，电极柱越窄，电极柱中的孔隙率越低。较窄的电极柱有利于缩短Li+在y轴方向上的扩散路径；而较低的电极柱孔隙率会增加Li+的扩散阻力。由于上述这两种因素的相互竞争，图3(b)和图3(c)中多级孔电极存在最优的低曲折因子孔道孔隙率0.16 。

由图3可知，对于含有不同低曲折因子孔道直径(d)的多级孔电极，存在不同的最优低曲折因子孔道孔隙率，说明低曲折因子孔道的最优孔隙率对其直径变化比较敏感。图4为低曲折因子孔道直径d=30μm和d=90μm时，含不同低曲折因子孔道孔隙率多级孔电极对应的Li+浓度分布图。当d=30μm时，Li+的浓度梯度随着d2/D2的增加而下降[图4(a)～(d)]。当d=90μm时，d2/D2从0.04 增加到0.16 ，浓度梯度先逐渐减小，然后当d2/D2从0.16 增加到0.25 ，浓度梯度又会增大[图4(e)～(h)]，这种浓度梯度的变化规律可以解释图3中能量密度的变化。另外，在相同的d2/D2下，d=90μm对应的浓度梯度远高于d=30μm对应的浓度梯度，说明d=90μm的多级孔电极中的扩散限制更强。对于d=30和90μm的多级孔电极，当电极柱保持相同的孔隙率时，电极柱的宽度却不一样。例如，当d2/D2=0.25 时，d=30和90μm对应的电极柱宽度分别为30和90μm。电极柱宽度越大，y轴方向上的扩散路径越长，也就说明d=90μm时Li+的扩散限制更强。对于多级孔电极，其低曲折因子孔道孔隙率越大，电极柱宽度越小，越有利于Li+的扩散；而多级孔电极中低曲折因子孔道所占的孔隙率越大，也意味着电极柱内的孔隙率越低，这将不利于Li+的扩散。因此，这两个竞争因素决定了多级孔电极存在最优的低曲折因子孔道孔隙率，且该最优孔隙率随低曲折因子孔道直径的增大而减小。

2.3 多级孔电极孔径的优化

图5显示了普通电极和具有不同低曲折因子孔道直径(d=10～40μm)多级孔电极对应的Ragone图。当低曲折因子孔道孔隙率相同时，能量密度随d的减小而增大。例如，d2/D2为0.04 、放电倍率为3C时，当孔径从40μm减小到10μm，对应的能量密度从309Wh/L增加到336Wh/L，见表3。当d2/D2固定时，孔径越小，电极柱的宽度越窄，而较窄的电极柱更有利于Li+的扩散，这解释了图5中能量密度与孔径之间的关系。此外，当d2/D2从0.04 增加到0.16 ，不同低曲折因子孔道直径对应的能量密度之间的差异逐渐变小。d2/D2越大，电极柱越窄，Li+的扩散限制越弱。在这种情况下，改变低曲折因子孔道直径不会显著改变能量密度。仅考虑能量密度和功率密度时，最佳的低曲折因子孔道直径为10 μm，此时以3C的放电倍率放电时，对应的能量密度比普通电极的能量密度高52.7%～89.1%（见图5和表3）。

表3 3C放电倍率下普通电极与具有不同低曲折因子孔道直径多级孔电极对应的能量密度Table3 Energy densities at the3C discharge rate for the conventional electrode and the hierarchically structured electrodes with different pore diameters

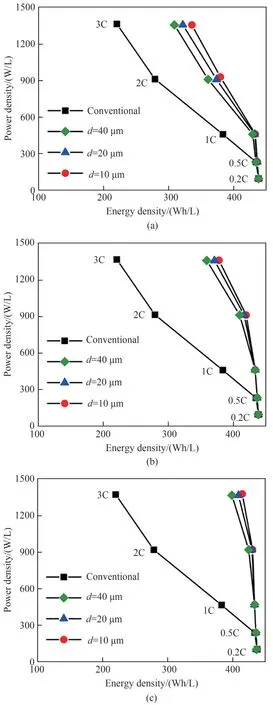
图5 普通电极与具有不同低曲折因子孔道直径（d=10、20和40μm）多级孔电极对应的Ragone图：(a)d2/D2=0.04 ；(b)d2/D2=0.09 ；(c)d2/D2=0.16 (模型参数：h=200μm，εt=0.36 ，其他参数列于表1)Fig.5 Ragone plots for the conventional electrode and the hierarchically structured electrodes with d=10,20,and40μm.(a)d2/D2=0.04 ;(b)d2/D2=0.09 ;(c)d2/D2=0.16 (Simulation parameters:h=200μm,εt=0.3 6.The other parameters are given in Table1)

2.4 总孔隙率和厚度的影响

上述研究在固定电极厚度和总孔隙率情况下，对多级孔电极中低曲折因子孔道孔隙率和直径进行了优化。本小节将进一步探究电极厚度和总孔隙率对电极性能的影响。图6对比了电极厚度在50～150μm时普通电极和多级孔电极对应的能量密度和功率密度。从图6可知，对于普通电极和多级孔电极，能量密度均随电极厚度的增大而增大。例如，当电极厚度分别为50、100和150μm时，普通电极在0.2 C放电倍率下的能量密度分别为212、323和391Wh/L。对于厚电极而言，惰性材料（如集流体和隔膜）所占的体积分数较低，因而能达到较高的能量密度。此外，多级孔电极与普通电极相比，随着电极厚度的增加，能量密度的提高幅度越来越大。例如，当厚度为50μm时，多级孔电极在3C放电倍率下的能量密度仅比普通电极高2.7%；而当厚度为150μm时，其能量密度比普通电极高55.3%，见表4。结果表明，对于厚电极，采用多级孔结构有利，采用优化后的多级孔电极可以显著提高电池性能。此外，功率密度随电极厚度的减小而增大，因为较薄的电极Li+扩散限制较弱，因而能达到较高的功率密度。例如，当厚度为150μm、放电倍率为3C时，功率密度为1622W/L；而当厚度为50μm、放电倍率为3C时，功率密度可达2635W/L。因此，当需要高功率输出时，采用薄电极是比较有利的。

图6 普通电极与多级孔电极在不同的电极厚度下的Ragone图：(a)h=50μm；(b)h=100μm；(c)h=150μm(模型参数：d=25μm，d2/D2=0.0625 ，εt=0.36 ，其他参数列于表1)Fig.6 Ragone plots for the conventional electrode and the hierarchically structured electrode under different electrode thicknesses.(a)h=50μm;(b)h=100μm;(c)h=150μm(simulation parameters:d=25μm,d2/D2=0.0625 ,εt=0.3 6.The other parameters are given in Table1)

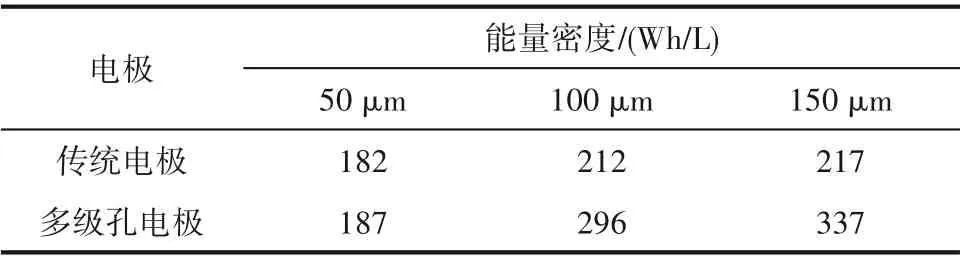
表4 3C放电倍率下普通电极与多级孔电极在不同电极厚度下的能量密度Table4 Energy densities at the3C discharge rate for the conventional electrode and the hierarchically structured electrodes with different electrode thicknesses

图7对比了总孔隙率为0.28 ～0.48 时普通电极和多级孔电极的能量密度和功率密度。当放电倍率较低时，电池的能量密度随总孔隙率的减小而增大。例如，当总孔隙率分别为0.48 、0.38 和0.28 时，普通电极在0.2 C放电倍率下的能量密度分别为355、424和491Wh/L。然而，当放电倍率较高时，较大的总孔隙率能达到更高的能量密度。当普通电极以3C放电倍率放电时，总孔隙率为0.28 对应的能量密度为252Wh/L，而总孔隙率为0.48 时的能量密度为295Wh/L，见表5。此外，随着总孔隙率的减小，普通电极与多级孔电极之间能量密度的差异越来越大，如总孔隙率为0.48 和0.28 时，多级孔电极在3C处对应的能量密度分别比普通电极高出2.4%和46.0%。当总孔隙率较低时，Li+在普通电极中受到的扩散限制较强，因此在其中引入多级孔道结构可以显著改善电极性能。

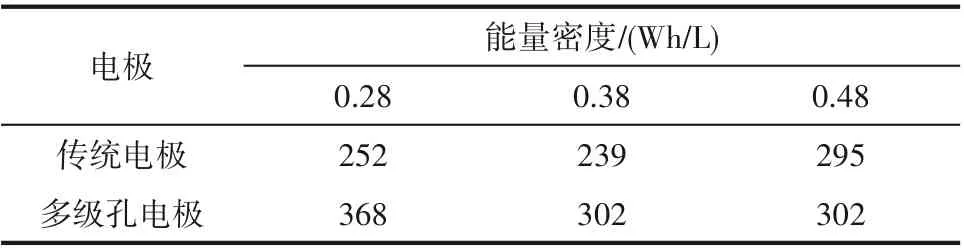
表5 3C放电倍率下普通电极与多级孔电极在不同电极总孔隙率下的能量密度Table5 Energy densities at the3C discharge rate for the conventional electrode and the hierarchically structured electrodes with different total porosities

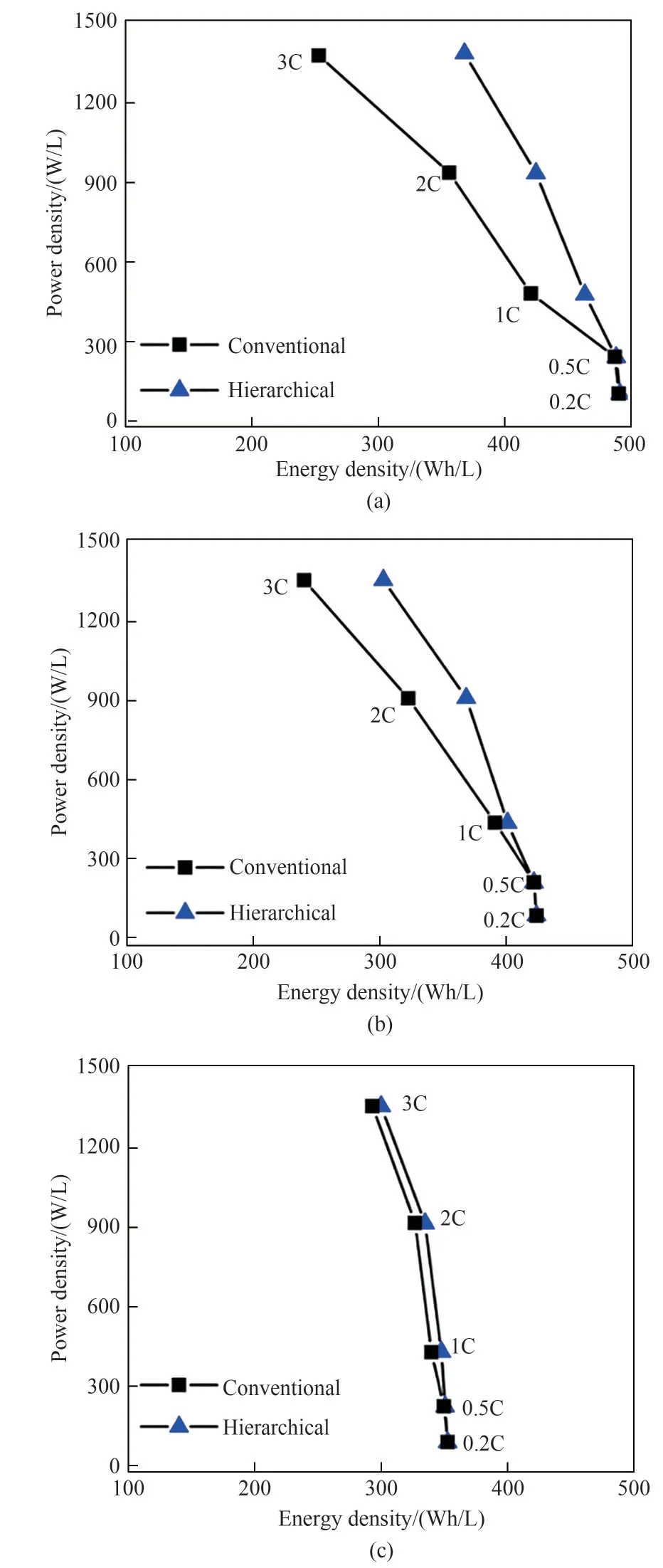
图7 普通电极与多级孔电极在不同电极总孔隙率下的Ragone图：(a)εt=0.28 ；(b)εt=0.38 ；(c)εt=0.48 (模型参数：d=30 μm，D=100μm，h=200μm，其他参数列于表1)Fig.7 Ragone plots for the conventional electrode and the hierarchically structured electrode under different total porosities.(a)εt=0.28 ;(b)εt=0.38 ;(c)εt=0.48 (simulation parameters:d=30μm,D=100μm,h=200μm.The other parameters are given in Table1)

3 结 论

本文基于Newman模型建立了一个二维模型，以模拟和优化含低曲折因子孔道多级孔电极的充放电过程。这种低曲折因子孔道垂直于集流体，充当Li+扩散过程中的“高速公路”，本文优化了低曲折因子孔道孔隙率和直径，还讨论了电极厚度和总孔隙率对电极性能的影响，得到以下结论：

（1）多级孔电极中低曲折因子孔道的最佳孔隙率高度依赖于其直径：直径d=30μm时最佳孔隙率为0.25 ，d=60～90μm时最佳孔隙率为0.16 。低曲折因子孔道的孔隙率越大，对应的电极柱越窄，越有利于Li+的扩散；但低曲折因子孔道的孔隙率越大也意味着电极柱中孔隙率减小，这不利于Li+的扩散。这两个相互竞争的因素决定了最佳低曲折因子孔道孔隙率的大小。

（2）多级孔电极中低曲折因子孔道直径较小时(d≤10μm)更优，此时电极柱较窄，可减弱Li+在电极柱中的扩散限制。

（3）增加电极厚度可以提高较低放电倍率下电池的能量密度，而减小电极厚度可以显著提高较大放电倍率下的功率密度。只有在低放电速率下，降低电池的总孔隙率才能提高能量密度。随着电极厚度的增加和总孔隙率的减小，多级孔电极能量密度的提高幅度越来越大。

本文建立的锂离子电池多级孔电极的数学模型和得到的研究结果能为锂离子电池的开发提供一个模型工具和一些指导。

符号说明

a——电极单元的比表面积，m2/g

D——分层孔结构两孔间的间距，μm

d——分层孔结构孔的直径，μm

d2/D2——分层孔道结构的孔隙率

x——沿孔道方向上的距离，μm

εadd——添加剂所占孔隙率