基于最近邻聚类的人群计数样本标注方法
2022-01-10张凯兵王华珂景军锋
张凯兵,张 婷,王华珂,景军锋
(西安工程大学 电子信息学院,陕西 西安 710048)
0 引 言
随着城市人口数量的快速增长和车辆的迅猛增加,城市的公共安全和交通管理面临巨大的挑战,尤其是公共场所的大型集会和节假日市民的出行面临严重的安全隐患。2015年元旦前夕,上海发生了严重的人群踩踏事件,造成多人伤亡。因此,公共场所的人群计数问题受到了人们广泛的关注。另外,人群计数在城市发展规划、商场人流监测、车流实时统计等方面应用前景广阔。尤其受新冠疫情的影响,人群拥挤度已成为疫情防控的一个重要指标。
人群计数问题面临非常多的挑战,主要包括人群尺度变化、复杂背景干扰、人群分布不均和缺乏标注样本等方面[1]。文献[2-3]针对人群尺度变化、复杂背景干扰和人群分布不均等问题提出了可行的解决方案。为了获取准确的预测结果,这些方法必须依赖充足的标记样本训练计数模型。但标记样本获取困难,且长时间乏味的标注数据容易人为地产生标记误差。因此利用有限的标记样本训练可靠的计数模型成为广大学者普遍关注的问题。
TAN等为了有效利用大量容易获取的无标记样本,提出了一种基于半监督弹性网的人群计数方法[4]。该方法利用连续视频帧之间的时序信息构造判别项,并利用k-means聚类方法选择具有多样性的标注样本,缓解缺乏标注样本情况下的人群计数问题。LOY等利用无标记样本之间潜在的流形结构构造半监督回归计数模型,同时通过主动学习选择少量代表性样本作为标记样本降低标记成本[5]。ZHOU等将样本选择任务作为子模块最大化问题,有效裁减冗余标记样本,并整合图拉普拉斯正则化和空间约束项到半监督弹性网回归模型中,提高预测的准确性[6]。ZHANG等将人群问题转换为半监督分类问题,同时联合利用标签适应性和流形平滑性学习高维特征空间到低维标签空间的线性映射,在减少标记样本的同时提升了模型的预测性能[7]。LIU等为了降低标注成本,使用更容易获取的二值分割标签作为代理任务训练特征提取器,再利用少量的人群标注样本训练密度图回归器[8]。为了利用大量的无标记样本监督网络的训练,SINDAGI等通过基于高斯过程的迭代学习框架生成无标记样本的伪标签监督网络参数的学习[9]。由于标注样本费时费力,ZHAO等提出一种基于主动学习的半监督人群计数框架,选取多样性的标记样本训练网络并利用分布分类器对齐标记样本和无标记样本[10]。此外,跨场景的人群计数[11]也可以有效地降低标注开销。WANG等提出通过合成数据集自动生成样本标签,采用风格迁移网络生成真实场景的样本,用于训练人群计数网络[12]。由于不同数据集存在明显的域差,导致模型的预测效果显著下降。尽管人群计数领域已经开源了多个大规模的数据集[13-15],但是利用这些数据集训练的模型泛化能力仍然有限,还不能有效地应用于真实场景中。此外,文献[16]通过数据增广的方法缓解了缺乏训练数据导致的模型过拟合问题。
针对上述问题,并受视觉任务中图像自动标注方法[17-18]的启示,本文提出了一种新的人群计数样本标注方法。考虑到含有相同或相近人数的视频图像在特征空间中距离相近的特性[19],提出了一种基于最近邻聚类的人群计数样本标注方法,以实现视频图像中人群数量的自动标注。该方法在特征空间中对全部无标记样本进行聚类,通过主动采样学习,从每一类样本中选取具有多样性和代表性的少量样本进行人群数量的标注,最后将标注样本的人数标签传播给该类别中剩余的无标记样本,该方法可高效地进行样本标注,并获得较高的准确性,显著降低了数据集的标注成本。通过该标注方法标记的样本也可以用于训练其他计数模型,降低训练样本的标注成本。
1 最近邻聚类与主动采样学习
对于包含人群的视频数据集,标注其中部分样本的人数进而训练计数模型,然后利用计数模型预测剩余样本的人数。通常,上述方法需要大量的标记样本训练模型,不利于实际应用。本文关注的重点是在如何降低标注成本的同时并保证模型的预测精度。
鉴于包含相同或者相近人数的视频图像在特征空间中距离相近的特性,表明在同一个视频场景中,一个视频帧与它的相邻帧可能包含相同或相近的人数。因此,利用相邻帧之间的结构关系可帮助视频数据集的标注。最近邻聚类的样本标注方法的总体框架如图1所示。
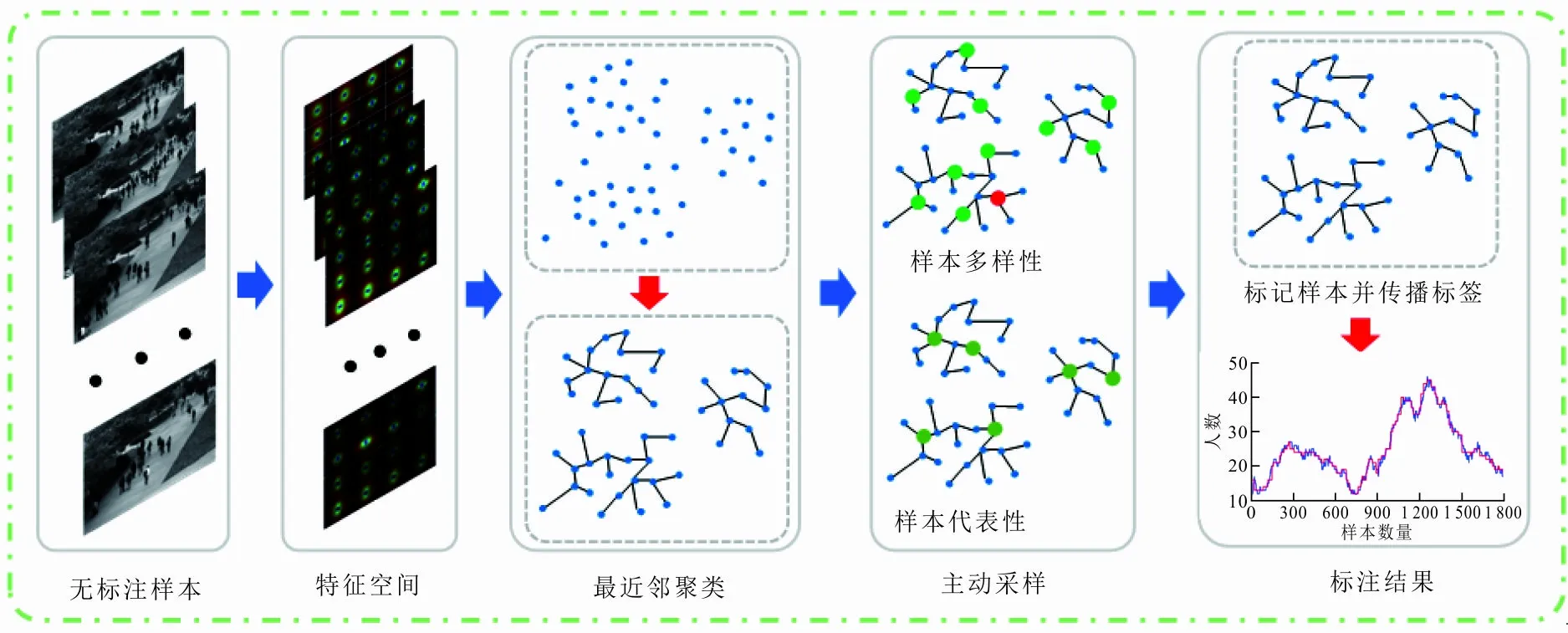
图 1 最近邻聚类的样本标注方法总体框架
从图1可以看出,该方法利用最近邻聚类构建结构关系,通过主动采样学习,从每类中选取少量具有代表性和多样性的样本进行标注,最后将标注的人数标签传播给其他未标记样本。
1.1 最近邻聚类
假设数据集X含有n个无标记视频样本,首先构造一个无向连通图G={V,E},其中V为特征空间中全部样本节点,E为欧式距离的邻接矩阵,E为矩阵E的对应集合,即
(1)
式中:Ei,j表示特征空间中第i个样本xi和第j个样本xj之间的距离。如果Ei,j在样本i的全部距离矩阵Ei中最小,则样本j为样本i的最近邻,即
(2)
根据最近邻样本定义确定全部样本最近邻关系,得到全部样本对应的邻接矩阵。根据样本间的最近邻关系,将全部样本划分为C组。最近邻聚类规则定义:如果样本i为样本j的最近邻,或样本j为样本i的最近邻,再或者样本i和样本j的最近邻为同一个样本,则它们属于同一类,即
(3)
式中:1表示2个样本属于同一类,0表示2个样本归属于不同类别。
全部样本根据最近邻关系可以划分到相应的类别中,近似地认为每一类中的样本含有相同或相近的人数。因此,仅标注每个类中少量代表性的样本,将人数标签传播给该类别中剩余的未标注的样本,样本的标注成本则显著降低。
1.2 主动采样学习
将全部样本划分为不同类后, 从每一类样本中选取代表性样本是样本标注方法的关键。本文通过主动采样学习[20]从每一类样本中选取代表性样本进行人数标注。主动采样学习不仅可以消除大量无标记样本中的冗余信息,还能克服异常值带来的负面影响。选取的样本应该尽可能表征每一类样本,使其具有代表性和多样性。根据文献[20],样本的代表性定义为
(4)

(5)
式中:M为中值滤波算子。此外,样本的多样性定义为
(6)
为了充分考虑样本的多样性和代表性,它们被给予相同的权重:
(7)
选取代表性样本进行人数标注并将它们的标签传播给该类样本中剩余的未标记样本,该方法根据多个代表性样本标注人数的均值作为该类样本的标签。因此选取少量代表性样本进行标注,可以减少标注代价。
本文提出的标注方法的算法步骤:根据式(3)对输入的大量无标记样本集X进行聚类,共聚为C类;再根据式(7)从每一类样本中选取代表性样本进行标注;最后将标记样本的人数标签传播给剩余未标记样本,则可以输出数据集X的标签集F。
2 结果与分析
文献[7]对比了其他纹理特征,证明Gist特征[19]对场景中的人群分布有较好的表征能力,因此本文采用Gist特征表征人群图像。在提出的样本标注方法中,所需标记样本的数量取决于聚类的数量和每一类样本中的采样个数。增加标记样本的数量,虽然提高了标注精度,但也增加了标注成本;反之,则会降低标注成本和标注精度。因此设置最佳的聚类数量和采样个数至关重要。本文分别从聚类数量和采样个数进行设置,选取最佳的聚类数量和采样个数。然后对比样本的标注精度和其他计数模型的预测结果。最后,将本文提出的样本标注方法所获得的标注样本构成训练集用于其他人群计数模型的学习。
2.1 数据集和评价指标
为了验证本文提出方法的有效性,分别在5个不同场景的视频数据集上进行验证。5个数据集中代表性样本如图2所示。

(a) UCSD (b) Fudan (c) Bus (d) Canteen (e) Classroom
图2中UCSD数据集[2]采集背景为校园人行道,包含2 000帧视频图像,人数在11~46之间变化。Fudan数据集[4]采集于教学楼入口,包含3个视频序列,共1 500帧视频图像,人数从0~15不等。Bus数据集[21]和Canteen数据集、Classroom数据集[22]分别拍摄于公交车和餐厅、教室等真实场景。5个数据集的细节信息见表1。

表 1 5个数据集的细节信息
使用平均绝对误差(mean absolute error,MAE)和均方误差(mean squared error,MSE)指标评价提出方法的预测效果。MAE和MSE在公式中分别定义为
(8)
(9)
式中:m表示数据集中样本的数量,Pi表示第i个样本的预测人数;Li表示第i个样本的真值人数。EMA用于评估计数模型的精确性,EMS反映人群计数模型的鲁棒性。
此外,本文提出一种新的精确性度量评价人群计数的预测精度。分类任务中通常使用精确性作为评价指标,但精确性直接用于评价人群计数不合适。事实上预测偏差小于一定阈值时,预测结果对实际应用并无太大影响。本文阈值设置为3,新的精确性度量指标定义为
(10)
式中:N表示测试样本的数量;‖·‖表示样本集中预测值P和真值L小于阈值的数量。
2.2 交叉验证
聚类数量和采样个数是影响标注样本数量和标注精度的重要因素。尽管增加聚类数量和采样个数可提升样本的标注精度,但也会增加标注代价。
以UCSD和Fudan数据集为例,分别对聚类数量和采样数量进行对比,结果见表2。
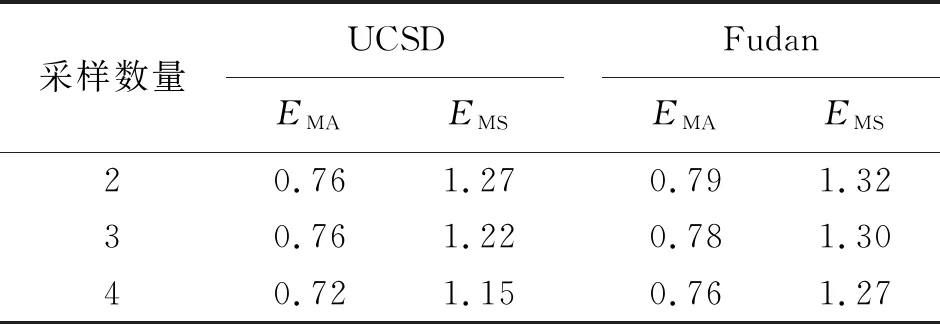
表 2 不同采样数量的实验对比
从表2可以看出,UCSD和Fudan数据集中采样个数从2增加到4,但数据的标注精度并没有明显提升,表明主动学习充分考虑了每一组聚类中样本的多样性和代表性,因此在5个数据集中将采样个数均设置为2。值得强调的是,当多个采样样本的人数标签不相等时,采用其平均值作为采样标签进行标签传播。不同聚类数量的实验对比如图3所示。
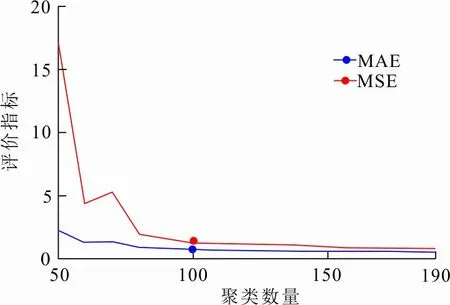
(a) UCSD数据集
从图3可以看出,在UCSD数据集中聚类数量达到100后,标注精度没有显著提升,UCSD数据集的最佳聚类数量为100; Fudan数据集的最佳聚类数量为120。因此最佳聚类数量与场景中人群变化复杂度有关,当场景中人群变化剧烈时,最佳聚类数量较大,反之则较小。
为了验证本文提出方法的标注成本远小于其他计数模型,对比在5个数据集中本文所需要的标记样本数量和其他监督学习模型所需的标记样本数量见表3。
从表3可以看出,本文提出的方法所需要的标记样本数量远小于监督学习方法训练集所需的数量。UCSD数据集所需的标记样本数量是监督学习方法的1/4,Fudan数据集所需的标记样本数量约为监督学习方法的1/2,在其他3个大规模数据集上所需标注代价也远小于监督学习方法所需要的标注代价。上述结果表明,本文提出的样本标注方法在标注成本上远小于监督学习方法。
2.3 有效性对比
利用聚类算法可以将标签相同或相近的样本划分为同一类,然后从每一组类别中选取代表性的样本进行标注,该样本标注的标签可以传播给该类中剩余的样本。为了验证本文采用的聚类方法和采样方法的有效性,选取k-means聚类和随机采样进行对比实验。不同聚类方法和采样方法的对比实验结果见表4。
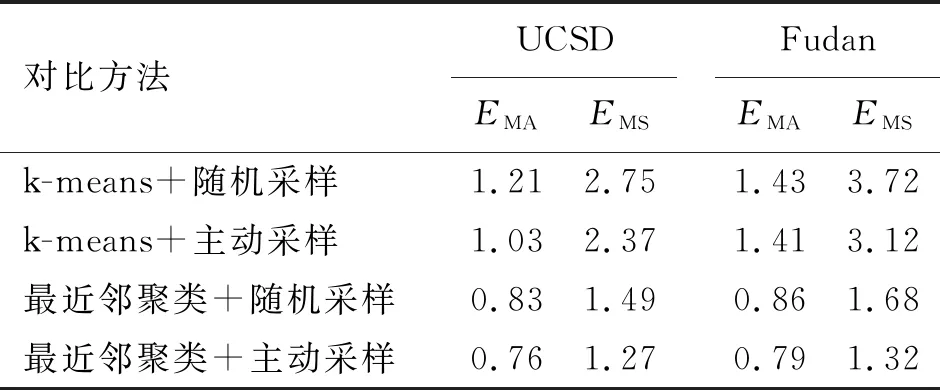
表 4 不同聚类方法和采样方法对比
从表4对比结果可以看出,利用本文提出的最近邻聚类方法与2种采样方法进行组合,在UCSD和Fudan 2个数据集上均取得较好的预测性能。主动采样与2种聚类方法进行组合后,在2个数据集上的标注结果也优于随机采样与2种聚类方法的组合,表明主动采样能够从每一组类别中选取更有代表性的样本。最近邻聚类与主动采样进行组合,在4种组合实验中获得了最好的标注结果,证明了最近邻聚类和主动采样进行组合的方法的有效性。
2.4 标注精度对比
标注精度是衡量样本标注方法的重要指标。本文对比了6种代表性人群计数方法:GPR[2]利用高斯过程回归从面积、周长等低级特征回归人群数量;SRRP[23]将人群计数问题转换为分类问题,并借助稀疏表示解决该分类问题;WANG等采用卷积神经网络的方法回归人群场景中的人数[24]。CSRNet设计了一种新的编码解码网络结构预测人群密度图[25]。LING等利用标签分布学习建模人群的标签模糊性,离散高斯分布初始化标签分布[21]。此外,VGG网络[26]是一种经典的神经网络,在其他计算机视觉任务上展示了良好的性能。本文利用预训练的VGG16网络来回归人群数量,其中将VGG16网络的3层全连接层替换为全局池化层,以减小参数量。为了进一步验证本文标注方法的有效性,在5个人群数据集上进行标注精度对比实验,具体结果见表5。
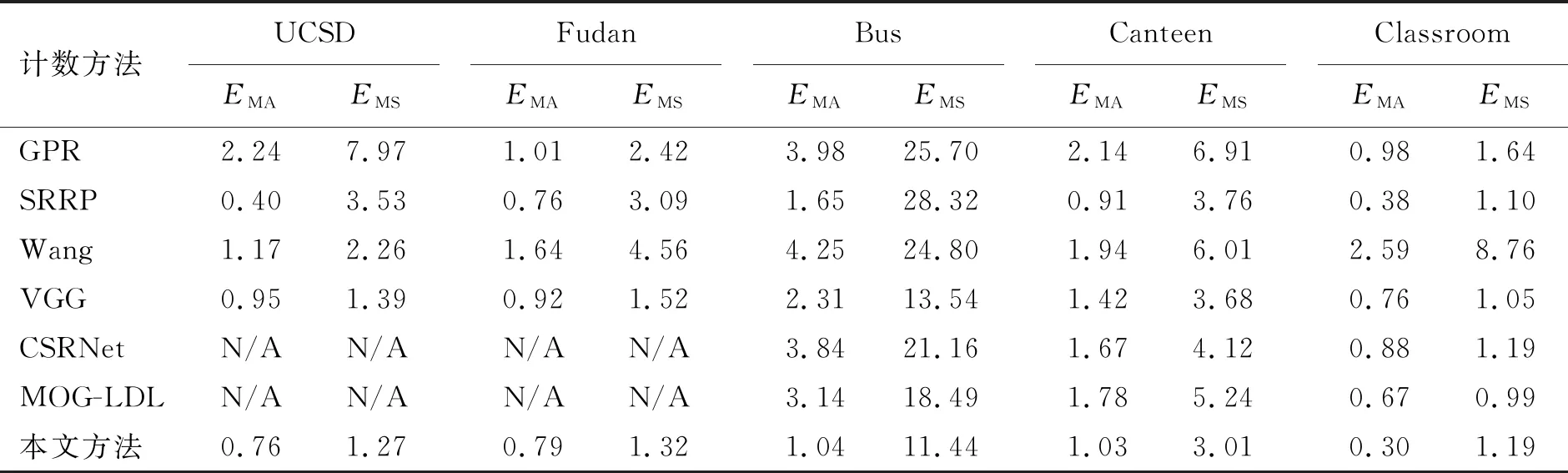
表 5 不同计数方法在5个数据集上的对比
从表5可以看出,本文提出的标注方法在5个数据集10个评价指标上有6项优于其他计数方法。本文提出的方法在UCSD、Fudan和Canteen数据集上MAE指标略大于SRRP,但MSE小于SRRP;在Bus和Classroom数据集上,MAE和MSE均优于SRRP。Bus数据集拍摄于公交车场景,图像质量较低;Classroom拍摄于教室场景,有复杂的背景干扰。对比SRRP,本文提出的方法表现出更好的泛化能力和鲁棒性。与深度学习的方法相比,本文提出的方法整体上优于VGG和CSRNet,仅在Classroom数据集上MSE略差于VGG。
综合上述结果可以看出,本文提出的标注方法不仅在标注成本上远低于采用监督学习方式的计数方法,而且提出的方法预测结果更好。为了更好地证实本文所提出方法的标注精度,图4展示了在5个数据集上标注结果与真值的对比。
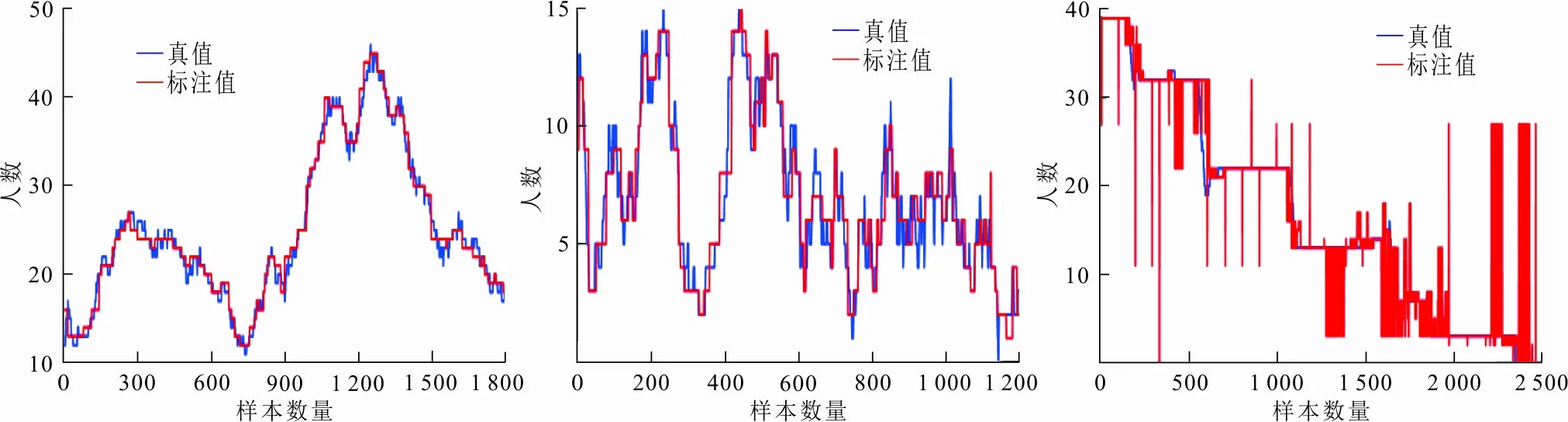
(a) UCSD数据集 (b) Fudan数据集 (c) Bus数据集
从图4可以看出,该方法在UCSD和Fudan数据集上取得了较为精确的标注结果,但在Canteen和Classroom数据集上存在一些偏差较大的标注值。总体来说,在4个数据集上标注效果较好,但在Bus数据集上的标注效果较差,因为Bus数据集记录了公交车场景中的人群变化,其中复杂的背景干扰和拥挤的人群分布导致了标注效果较差。
2.5 训练其他人群计数模型
为了进一步评估本文人群数量标注方法的有效性,利用标注结果训练其他人群计数模型,通过评估预测结果与真实值之间的差异,验证本文人群数量标注方法的有效性。为此,分别采用训练集真值和通过本文标注方法获取的标注值训练3种计数模型,测试集则使用真值进行评估。由于Gist特征比低级特征对人群场景有更好的表征能力,因此本文在训练GPR计数模型时使用Gist特征作为特征描述符。3种计数方法在5个数据集上的对比结果见表6。
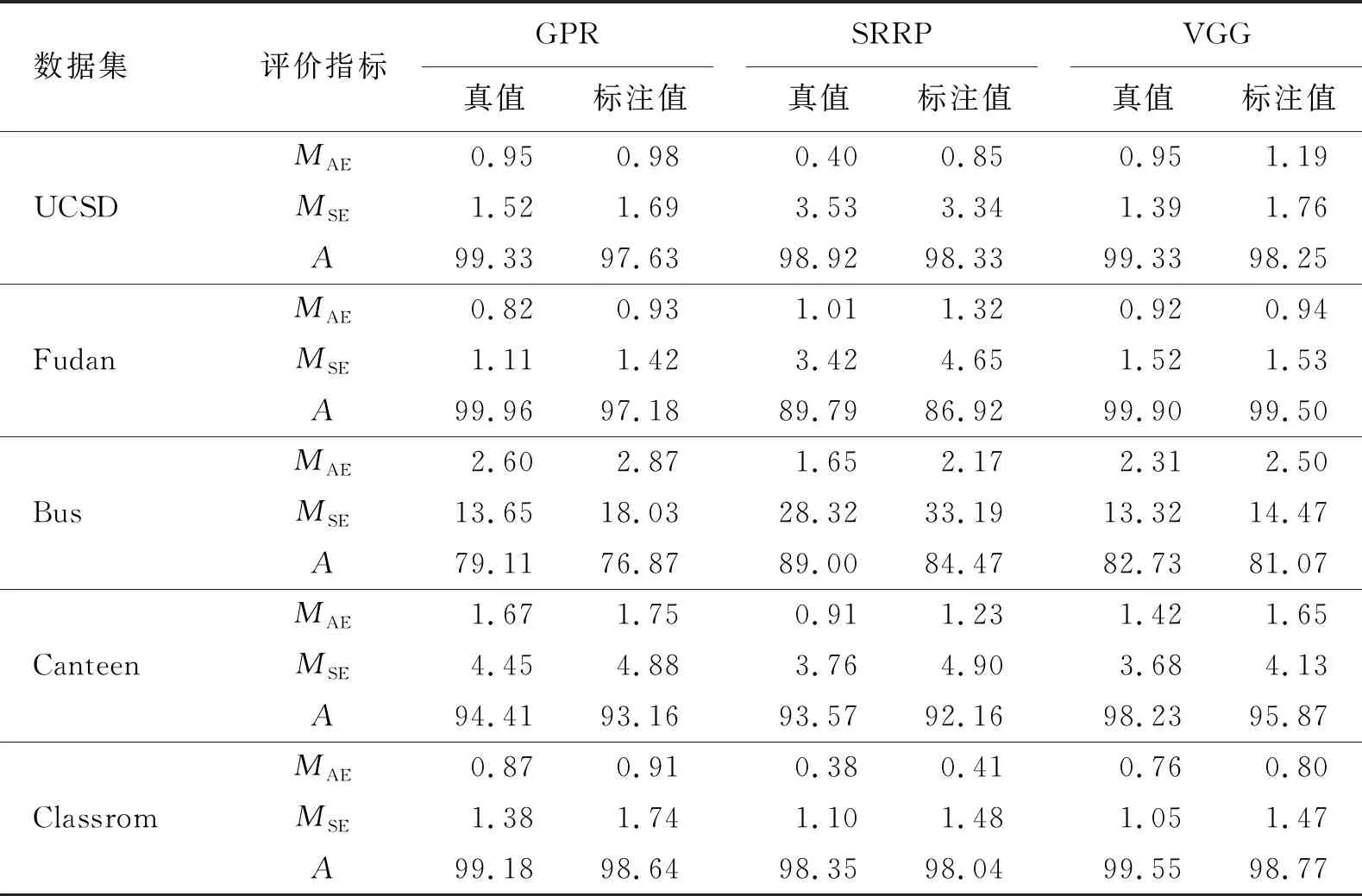
表 6 真值和标注值训练的计数模型结果对比
从表6可以看出,使用标注值训练的计数模型和使用真值训练的计数模型预测精度几乎一致。这是由于在真值的标注过程中,可能存在人为标注误差,当标注误差与真值相差较小时,并不影响模型的训练结果。因此本文提出的标注方法可以为其他计数模型提供训练集所需的标记样本。
由上述结果可知,本文提出的方法在UCSD和Fudan数据集上取得了精确的标注效果,在Canteen和Classroom数据集上获取了较为精确的标注效果,在Bus数据集上标注效果较差。该标注方法在为其他计数模型提供样本标签时受训练集的标签精度影响较小。
为了进一步评价标注方法的有效性,本文分别利用真值和标注值训练同一计数模型并对比预测结果,预测结果一致表明本文提出的标注方法可用于训练其他计数模型。5个数据集上的真值和标注值训练VGG计数模型对比如图5所示。

(a) 真值在UCSD数据集上训练的的计数模型 (b) 标注值在UCSD数据集上训练的计数模型
图5左侧表示真值训练的计数模型,右侧表示标注值训练的计数模型。对比结果可知,利用真值和标注值为监督信息训练的计数模型在预测性能上没有明显差别,表明本文提出的标注方法可以为其他计数模型提供训练样本的标签。
3 结 论
1) 提出一种基于最近邻聚类和主动采样学习的样本标注方法。该方法利用含有相同或相近人数的视频图像在特征空间中距离相近的特性,实现人群数量的自动标注。
2) 采用最近邻聚类在特征空间中对样本进行聚类,通过主动采样学习,从每一类样本中选取少量具有代表性和多样性的重要样本进行人数标注。
3) 本文提出的样本标注方法具有较低的标注偏差,利用标注样本训练的计数模型和利用真值训练的计数模型预测结果具有较好的一致性。
