基于BP神经网络的单钉铆接最大变形预测
2022-01-10陈永当秦淑娟顾金芋侯梦楠
陈永当,刘 善,秦淑娟,顾金芋,侯梦楠
(西安工程大学 机电工程学院,陕西 西安 710048)
0 引 言
铆接是飞机装配领域最重要的机械连接方式之一,工艺过程简单、质量轻、连接强度高且稳定可靠[1-2]。变形是铆接工艺的固有特点,在多钉铆接时变形逐渐叠加,并导致装配体的整体变形[3-5]。因此,针对铆接变形量进行预测研究具有一定的工程意义。
通过实验研究和有限元数值模拟方法,国内外学者对铆接变形问题进行了大量研究[6-8]。实验研究铆接变形通常需要耗费大量材料和时间,而有限元数值仿真法被证明为有效的替代方法[9-11]。文献[12]利用有限元分析方法建立了铆接件局部到全局尺寸误差计算框架来预测铆接件的整体变形。文献[13]使用静应力和非线性显式有限元模型对飞机板和纵向加筯肋的装配进行了模拟,并通过实验验证了有限元方法的有效性。文献[14]利用有限元条件下的简化模型对自穿孔铆接引起的装配变形进行了预测。文献[15]采用仿真与实验相结合的方法,针对铆接壁板变形问题进行研究,通过分层映射算法建立了铆接变形预测模型。
虽然铆接工艺较简单,但影响铆接变形的因素较为复杂,属于非线性问题,变形与各因素之间的具体关系很难用一般表达式表示,而神经网络在建模与预测方面具有独特优势[16]。BP神经网络是最常用的神经网络模型之一,具有很强的非线性拟合能力,是一种性能优良的前馈型神经网络[17-18]。因此,本文选取BP神经网络模型对单钉铆接最大变形量进行预测。又由于单钉铆接变形数值模拟涉及参数较多,任一参数变化都需重新建模,而模型的拟合需要一定量的样本数据,因此本文采用Python语言进行参数化建模,并进行批处理运算,既简化了建模过程,又提高了数值模拟效率。
1 铆接变形预测模型
1.1 预测模型变量设计
在实际铆接过程中,工艺人员通过改变铆钉直径、钉杆长度、板件孔径及压铆位移量来控制和调整铆接的质量。因此,本文以这4个参数作为输入变量,表示为X={x1,x2,x3,x4},以最大变形量为输出变量,表示为Y={y}。
LHS方法能够在预定的样本空间抽出较为均匀的试验点[19],因此本文采用LHS方法进行抽样,生成500个实验样本,并随机抽取450个样本作为模型的拟合,余下样本作为精度测试。在拟合模型之前,对输入参数和输出参数进行无量纲归一化处理,将数值范围变换至[0,1]内,其归一化函数为
(1)
式中:xi,max为变量xi中的最大值;xi,min为变量xi中的最小值,i=1,2,3,4。
1.2 BP神经网络预测模型
基本的BP神经网络由输入层、隐含层和输出层3部分组成,如图1所示。各层具有不同的作用,输入层直接连接输入变量,隐含层实现了输入层到隐含层的非线性映射,输出层实现隐含层输出变量的线性输出。

图 1 BP神经网络模型
本文设置3层神经网络层数,输入层1个,隐含层1个,输出层1个;输入层变量节点个数L=4;输出层变量节点个数M=1;隐含层节点数N,根据式(2)计算得到,其中α取值范围为0~120[20]。
(2)
采用BP神经网络模型进行数据拟合,最大变形量Y与输入变量X之间的函数关系可表示为
(3)
式中:wln为输入层和隐含层之间的连接权值;wn为隐含层和输出层之间的连接权值;bn为隐含层的阈值;bk为输出层的阈值;φ(·)为隐含层的传递函数。本文隐含层激活函数为Tansig,输出层的传递函数为φ(·),输出层激活函数为Purelin。训练神经网络模型时,精度设置为1×10-4,最小梯度设置为1×10-30。
2 铆接变形参数化建模
2.1 参数化建模流程
为了简化建模过程、提高效率,使用Python语言对单钉铆接变形数值模拟进行参数化建模和批量运算。在参数化建模的过程中,对变化的参数进行参数化处理,对不变的参数采用固定设置,进而实现数值模拟的自动参数化建模,然后利用ABAQUS软件进行求解得到数值仿真结果,其铆接变形参数化建模流程见图2。

图 2 铆接变形参数化建模流程
2.2 参数定义
本文以平锥头铆钉为研究对象,尺寸结构参照标准HB 6302—2002。根据铆接工艺特点,单钉铆接参数化建模涉及几何建模、材料属性定义、载荷及分析步定义、边界条件及接触定义、网格划分等内容。
1) 几何建模:模型结构见图3,主要由上下板件、铆钉及铆接工具4部分组成。Dr和L分别为铆钉直径和钉杆长,DA和tA分别为上下板件的孔径和厚度[21],Dr=5.00 mm,L=10.00 mm,DA=5.08 mm,tA=2.00 mm。
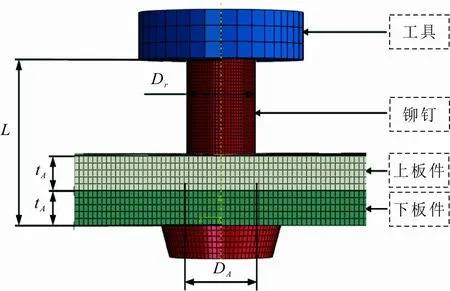
图 3 铆接模型结构
2) 材料属性定义:铆钉和上下板件材料分别为2A10和7075铝合金,密度分别为ρr和ρA,弹性模量分别为Er和EA,泊松比分别为μr和μA,ρr=2 790 kg/m3,ρA=2 800 kg/m3,Er=69.0 GPa,EA=71.0 GPa,μr=0.31,μA=0.31。铆钉和板材均为非线性材料,在铆接过程中塑性屈服不明显,采用Johnson-Cook模型描述7075和2A10铝合金材料的本构关系[22-23],可表示为
(4)
式中:ε0为等效塑性应变;ε1为应变率;ε2为参考应变率;A、B和C分别为屈服强度、硬化模量和应变敏感系数;T、Tr和Tm分别表示为试件温度、参考温度和材料熔点;m和n为无量纲常数。铝合金7075材料中,A=503 MPa,B=670 MPa,C=0.018,m=1.78,n=0.69;铝合金2A10材料中,A=243 MPa,B=618 MPa,C=0.010,m=1.60,n=0.20。
3) 载荷及分析步定义:铆钉的最大压缩变形量为Smax=3.20 mm,铆接过程分2步进行模拟,加载与卸载的位移荷载曲线近似正弦函数[17],时间均为0.5 ms。
4) 边界条件及接触定义:边界条件设置见图4。板件端部固定约束,铆接工具底部受x轴和y轴位移和旋转的约束,仅允许在z方向上移动,其中ux、uy和uz分别表示沿x、y和z方向的位移量。当某方向的位移量为0表示沿该方向上固定约束。铆接模型中的接触关系包括铆钉与上下板材的接触、上下面板之间的接触、工具与铆钉的接触,接触方式选择surface-to-surface contact类型。

图 4 铆接有限元模型
5) 网格划分:如图4所示,大变形区域集中于铆钉和镦头覆盖的板件部分,其相对于板件整体结构而言区域范围较小,考虑仿真精度和计算时间成本,因此对大变形区域进行网格细化。在计算过程中为消除网格质量和数量对计算结果带来的误差,需进行网格无关性验证[24]。本文采用相同质量的4种不同网格对铆接过程进行仿真,结果如表1所示。最大误差均小于仿真允许误差5%,满足网格无关性要求。

表 1 网格无关性验证
2.3 数值模拟计算结果
铆接后的应力变化云图及板件铆接后位移云图见图5,板件变形区域主要集中在钉孔周围,最大变形量大约为0.091 2 mm。
3 模型预测结果分析
使用BP神经网络模型对单钉铆接最大变形量进行预测,训练结果如图6所示。
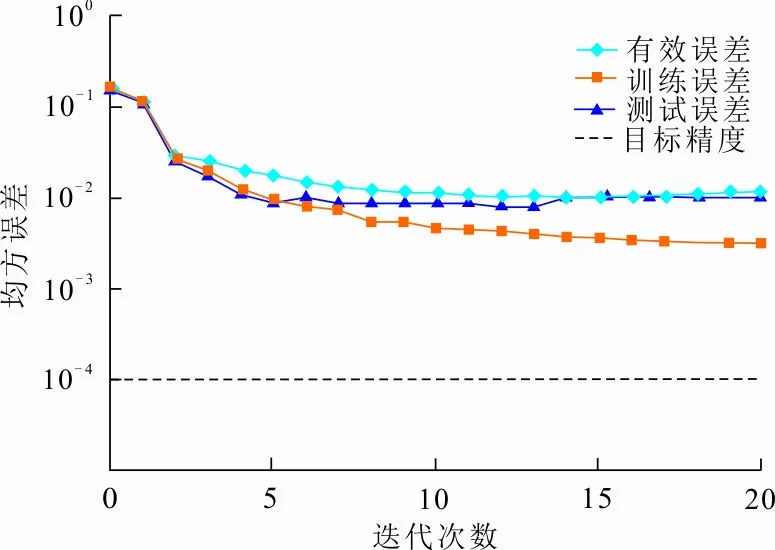
图 6 训练误差曲线
从图6可以看出,迭代14次后,训练误差趋近于0.01;迭代20次后终止训练,训练误差为0.008。
BP神经网络模型预测结果与实际值对比结果如图7所示。

图 7 预测值与实际值对比
为了评估预测精度,需要采用一些统计学方法,平均相对百分比误差EMAP可以较好地反映出预测绝对误差值的真实情况,均方根误差ERMS可以很好的表现出数据拟合的好坏[25]。因此,本文选取常用的平均相对百分比误差和均方根误差对结果进行评价:
(5)
(6)

根据式(5)和(6),得到BP神经网络模型预测相对百分比误差,见图8。

图 8 BP神经网络模型预测相对百分比误差
图8中,最大相对误差为13.01%,平均相对误差为4.14%,均方根误差为0.00517,平均预测精度达到95.86%。根据预测结果可知,BP神经网络模型在单钉铆接最大变形量预测方面具有较高的预测精度。
4 结 语
在分析铆接变形基础之上,采用Python语言对ABAQUS进行二次开发,实现了参数化建模和批量处理,简化并缩短了建模周期。将BP神经网络运用于最大铆接变形量预测,结果表明:该方法拟合能力强、性能好、预测精度较高。
