重型直升机飞行动力学刚弹耦合建模及空中共振稳定性分析

2022-01-10王洛烽陈仁良

航空学报 2021年12期

王洛烽，陈仁良

南京航空航天大学航空学院直升机旋翼动力学国家级重点实验室，南京 210016

重型直升机因为其强大的载重能力、特殊的悬停能力以及相对于地面运输车辆和固定翼运输机更加灵活的机动能力，在军事运输、抢险救灾中有着不可替代的作用。自2008年5月12日汶川大地震凸显了重型直升机的重要性以来，中国一直将重型直升机的研制作为重点发展项目，但受技术水平所限和研制经验不足，对其认识还不够充分，若基于中小型直升机的飞行动力学模型进行分析可能会因为忽略了某些重要因素而导致分析不准确，因此需要对重型直升机的固有特性进行针对性地建模和分析。

重型直升机有着相对更低的旋翼转速，导致旋翼整体模态与低阶机体弹性模态的频率范围重叠，且比通常情况下更加接近直升机刚体运动模态的频率范围，这意味着重型直升机的刚体运动、旋翼整体运动和低阶机体弹性振动三者间的相互耦合相对于普通直升机更为突出[1]，因此在重型直升机飞行动力学建模时需要考虑旋翼机体的刚弹耦合以提高分析准确性。

除了由于旋翼后退型摆振和直升机刚体运动及旋翼挥舞运动耦合产生的空中共振外，直升机弹性机体的某阶振动使旋翼总重心在旋翼旋转平面内振动也可能导致空中共振或出现类似于空中共振的高频瞬态振动[2]，后者虽不如前者严重，但会让驾驶员感受强烈，同样应当避免。因此为了研究重型直升机的空中共振现象，建立旋翼机体刚弹耦合模型也非常必要。此外，空中共振还与桨叶弹性变形有关，桨叶变形导致的挥舞摆振运动耦合关系的变化会影响到旋翼后退型摆振运动，继而使空中共振特性发生变化，并且由于重型直升机桨叶尺寸更大，变形更大，从而对空中共振的影响更严重，因此还需要在模型中考虑桨叶弹性变形。

然而，尚未有公开文献研究直升机飞行动力学特性时同时考虑机体和桨叶的弹性变形，大部分研究在飞行动力学综合建模分析时至多考虑桨叶的弹性变形和旋翼尾迹。李攀[3]基于旋翼非定常自由尾迹和伽辽金有限单元法建立了适用于直升机机动飞行的飞行动力学模型，计算得到的旋翼载荷与飞行试验结果的吻合程度优于CAMRAD II的结果，但该研究对象是10 t级的UH-60A，无需考虑机身的弹性变形。

在直升机研究领域，同时考虑机体和桨叶弹性变形的相关研究都着眼于旋翼/机体气弹耦合动稳定性，包括旋翼挥摆扭耦合稳定性、地面共振和空中共振[4-5]，但这些研究中建立的模型往往是基于理想情况，少有考虑实际飞行状态，这说明在直升机的研究中，飞行动力学问题与气弹动稳定性问题的研究是分开的。

在固定翼飞机、高超声速飞行器和空间飞行器等研究领域有着在飞行动力学分析中考虑机身弹性变形的先例，这是因为这些飞行器的尺寸大、结构频率低，若忽略变形会影响分析精度，这一点与重型直升机的固有特性类似，这些研究使用的建模方法包括平均轴系法[6]、准坐标系法[7]和瞬态坐标系法[8]。在CH-53K直升机的研制过程中，使用基于AB阵的线性方法考虑了机体的弹性变形[9]，但仅考虑了桨毂载荷对机体弹性变形的作用，并没有涉及机体弹性变形引起的旋翼桨毂运动，因此没有用到直升机非线性旋翼/机体刚弹耦合建模方法。Cribbs等[10]使用平均轴系法建立了直升机旋翼/机体耦合模型，并基于主动结构响应控制研究了直升机机体的减振，但Meirovitch和Tuzcu[11]质疑Cribbs的模型并不能真实反映柔性机身的变形情况并提出了解决该问题的方法，该方法涉及到的符号运算量太大且无法简化，因此直升机的旋翼/机体耦合直升机飞行动力学刚弹耦合建模方法尚存在争论，并无统一的建模手段。

本文研究目标是开发一种适用于重型直升机的飞行动力学建模方法，可以同时考虑桨叶和机体的弹性变形，并且能够模拟真实飞行状态下重型直升机的刚弹耦合特性。为了实现这一目标，第1节结合传统飞行动力学建模方法和柔性多体动力学建模方法[12]，简化了方程的推导过程和最终的表达式，使用阻抗匹配法[13-14]显式地处理了旋翼/机体耦合问题，将桨叶和机体的结构动力学方程表示成统一形式，并基于浮动坐标系法[15](即准坐标系法)建立了直升机飞行动力学旋翼机体刚弹耦合模型。为了在满足飞行动力学和低阶旋翼机体耦合分析精度的同时尽可能地降低模型的复杂度以突出重点和提高计算效率，假设：挥舞/摆振铰在同一位置，因为重型直升机通常采用铰接式旋翼。第2节验证模型的准确性，由于重型直升机验证数据缺乏，本文通过分别验证的方法，首先基于现有的中小型直升机的飞行试验数据验证了直升机刚体运动特性，接着利用旋翼/机体动稳定性试验数据验证了旋翼/机体耦合动力学特性。第3、4节使用本文建立的模型针对重型直升机算例分析了飞行动力学耦合特性和空中共振稳定性。

1 重型直升机飞行动力学刚弹耦合建模

多体动力学中将飞行器归类于无根系统，即不与静止坐标系相连的系统，常常将该系统中质量最大的部件作为基础，其他部件通过约束连接在该基础上，对于重型直升机，将质量最大的机体作为基础，旋翼、尾桨和平/垂尾作为连接在该基础上的部件。虞志浩[16]曾基于多体动力学建立旋翼系统的动力学分析模型，研究了旋翼气弹稳定性，优点是方程形式统一，能够隐式地处理好旋翼和机体的耦合关系，但这种方法建立的模型由于其过高的复杂度，难以用于飞行动力学特性分析中。

不同于多体动力学，在传统的直升机飞行动力学建模方法[17]中，首先求出各片桨叶对桨毂的惯性力再累加到机体上，由于是刚性桨叶，可以显式地推导出从桨毂加速度到桨毂载荷的阻抗矩阵。机体的六自由度刚体运动会体现在桨毂的运动中，同样容易得出从机体运动加速度到桨毂加速度的阻抗矩阵，这样就可以通过显式的阻抗匹配法处理旋翼/机体耦合关系。当考虑桨叶弹性变形时，旋翼阻抗矩阵就变得更加复杂，李攀[3]采用数值方法在每个计算步中求出了旋翼的阻抗矩阵，解决了桨叶弹性变形和机体运动的耦合问题。

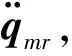
(1)

式中：H代表从右下标到右上标的阻抗矩阵；f代表不包含加速度的方程右端项；I是单位矩阵。

1.1 弹性机体动力学模型

根据多体动力学的内容，空间中的自由柔性体在浮动坐标系(准坐标系)下的运动方程可以写为

(2)

式(2)可作为直升机机体的运动方程，浮动坐标系对应了体轴系，广义加速度可表示为

(3)

在传统的直升机飞行动力学建模中，通常将体轴系下的速度和角速度作为刚体运动的状态量，因此将式(3)对应的广义加速度更改为

(4)

相应的，对式(2)对应的动力学方程也进行了更改，同时考虑重力的影响并加入角标得到

(5)

式(5)中，质量矩阵的组成部分Mjk会随着机体变形量的变化而变化，但由于直升机的机体变形量较小，可以忽略Mjk中与变形量有关的部分，从而弹性机体运动方程的质量矩阵为常数矩阵。广义外力Qe,F来自于机体上的各部件，由部件作用于机体上的气动力和惯性力组成，对于常规构型的重型直升机，这些部件包括旋翼、尾桨、平尾和垂尾，由于本模型主要考虑旋翼/机体耦合，且后三者质量较小，可假设尾桨、平尾和垂尾的质量为零，只对机体作用气动力，可以将广义外力表示为

(6)

除旋翼以外的其他气动部件的质量很小，可以忽略机身与这些气动部件的惯性耦合，但这些部件的局部运动速度由直升机的刚体运动和机体的弹性变形组成，体现了弹性变形对这些部件的气动-弹性耦合。旋翼对机身的作用力既包括由于机体刚体运动和弹性变形导致的桨毂加速度的惯性力，也包括旋翼内部挥舞摆振和桨叶弹性变形运动导致的惯性力，此外，与加速度项无关的桨毂载荷中还包括了机体刚体运动和弹性变形导致的桨毂运动速度，体现了气动-弹性耦合。

1.2 弹性桨叶旋翼动力学模型

基于挥舞/摆振铰在同一位置的假设，旋翼模型由桨毂S、挥舞/摆振铰H和弹性桨叶组成B，对应的坐标系分别是桨毂不旋转轴系S、桨毂旋转轴系H和桨叶坐标系B。类似于多体动力学中的递推方法，可以基于机体当前的运动状态和相邻坐标系间的相对运动得到桨叶的运动状态，同时将状态量表示在绝对坐标系下以避免出现牵连加速度，最终得到桨叶的运动状态为

(7)

(8)

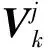
(9)

相对于式(5)中机体的运动方程，由于桨叶受挥舞/摆振铰的约束作用，桨叶的运动方程中还应当包括约束力部分，用Qc表示，因此将桨叶的运动方程写为

(10)

式中：约束力可以表示为

(11)

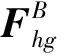
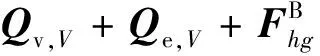
(12)

(13)

(14)

将式(8)代入式(12)～式(14)，并按照已知量和未知量整理可以得到约束力方程、挥舞摆振运动方程和桨叶弹性变形方程。

1)约束力方程与桨毂载荷

式(12)可整理为

(15)

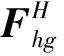
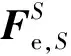
(16)

(17)

2)挥舞摆振运动方程

式(13)可整理为

(18)

式中：Mωω表示桨叶在桨叶轴系下的转动惯量，记桨叶绕挥舞/摆振铰的转动惯量为Ib，桨叶绕变距铰的转动惯量为Ip，则有

(19)

由于桨叶的变矩运动的转动惯量Ip极小，在飞行动力学建模中可忽略其影响，则式(18)中对应桨叶变矩运动的第2行方程可以省去，仅保留与桨叶挥舞和摆振运动有关的方程，即

(20)

(21)

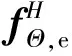
3)桨叶弹性变形方程

式(14)可整理为

(22)

1.3 旋翼气动力计算模型

(23)

从式(23)中可以看出，桨叶微段的运动速度考虑了桨叶的刚体运动和弹性变形运动的影响，体现了桨叶的气动弹性耦合。

1.4 旋翼/机体耦合运动方程

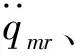
(24)

(25)

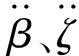
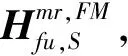
(26)

(27)

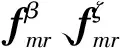
(28)

将式(28)代入式(27)可以得到总旋翼/机体耦合运动方程(1)中旋翼部分运动方程中的阻抗矩阵和右端项。将式(28)代入矩阵形式的桨毂载荷式(26)，再将式(26)代入机体运动方程的广义外力项式(6)中，并结合机体运动方程(5)，即可得到总旋翼/机体耦合运动方程(1)中机体部分运动方程中的阻抗矩阵和右端项。

至此，旋翼/机体耦合动力学方程已经推导完成且公式中的所有项存在显式的表达式，不需要通过数值方法求解，能清晰地体现机体和桨叶弹性对系统的影响。

2 重型直升机飞行动力学模型验证

在重型直升机验证数据缺乏的情况下，为了验证第1节建立的模型的正确性，采用高低频分开验证的方法。首先基于UH-60A直升机的飞行试验数据[18]验证了该模型的低频刚体运动特性，接着基于Bousman的旋翼/机体耦合试验数据[19]验证该模型的高频旋翼/机体耦合特性，这样就能够确定模型的合理性和准确度。

2.1 直升机低频刚体运动特性验证

基于UH-60A直升机的试飞数据验证该模型的低频刚体运动特性，UH-60A的主要参数可参考文献[20]。

图1对比了UH-60A前飞配平曲线的模型计算值和试飞试验值，二者吻合良好。其中δcol、δlat、δlon和δped分别表示直升机的总距杆量、横向操纵杆量、纵向操纵杆量和脚蹬位移量，φ和θ分别表示直升机的滚转角和俯仰角。

图1 UH-60A前飞配平曲线验证图

2.2 直升机高频旋翼/机体运动特性验证

基于Bousman的试验数据验证旋翼/机体耦合模型，该试验在地面上利用转动铰和支撑杆模拟机身，通过设置杆的刚度调整机体滚转和俯仰运动刚度，用式(1)中改进的显示阻抗匹配法建立该试验系统模型，如图2所示。

图2中用简图的方式表示了实际模型并建立了坐标系，坐标系(O-XYZ)E表示地面铰坐标系，原点在地面上的转动铰处，X轴代表滚转运动，滚转角用φE表示，Y轴代表俯仰运动，俯仰角用θE表示；坐标系(O-XYZ)S表示旋翼桨毂轴系，X、Y、Z轴与地面铰坐标系平行。

图2 Bousman的旋翼/机体耦合试验模型

(29)

(30)

式中：hS是地面铰到桨毂中心的距离；T1和T2是常数矩阵。

桨毂状态量导数为

(31)

地面铰接系统的状态方程可以表示为

(32)

式中：Iφ和Iθ分别是滚转和俯仰转动惯量；mφ和mθ分别是计算滚转和俯仰运动时的质量；hφcg和hθcg分别是计算滚转和俯仰时的质心距离地面较的高度。

式(31)、式(32)表示了Bousman试验配置中旋翼与机体的相互作用关系，结合第1节中对旋翼的建模，并利用阻抗匹配法处理旋翼/机体耦合关系，就可以得到该试验验证模型的旋翼-支座阻抗匹配模型：

(33)

将Bousman试验中的配置1对应的系统参数代入模型，接着基于多桨叶坐标变换方法计算转速从0～1 000 r/min时各系统模态的频率和特征值实部，计算值与试验值的对比结果如图3和图4所示。图中标记的含义分别为：Pitch(机体俯仰)；Roll(机体滚转)；vi(均匀旋翼入流)；FP、FC和FR分别代表旋翼挥舞前进型、集合型和后退型；LP、LC和LR分别代表旋翼摆振前进型、集合型和后退型。

观察图3中转速为700～800 r/min的曲线，可以发现在该转速范围内，摆振后退型与滚转运动频率相近，这导致图4中相同转速范围内摆振后退型的特征值实部发生明显变化，使其变为正值，意味着摆振后退型出现发散现象，同时机体滚转运动也出现了明显变化，但可能由于测试手段有限，无法在试验结果中体现出来，只清晰地反映在了滚转运动的特征值实部变化曲线中。此外，由于旋翼-机体耦合的存在，基座的滚转和俯仰模态在实际表现中的区别并不明显，它们会互相耦合，形成圆锥形运动，这样的圆锥形运动很难判断其属于滚转或是俯仰模态，也难以通过试验方法确定其阻尼，这也是图4中滚转和俯仰模态误差较大的原因，该误差同样在Bousman的模型验证对比中体现出来。因此，图3和图4所示的结果表明本文建立的模型能够较完整地体现旋翼/机体耦合特性，且能够较精确地反映系统的模态频率和阻尼，从而可以用于重型直升机飞行特性和空中共振稳定性的分析。

图3 Bousman旋翼/机体耦合试验配置1的系统各模态频率随旋翼转速变化

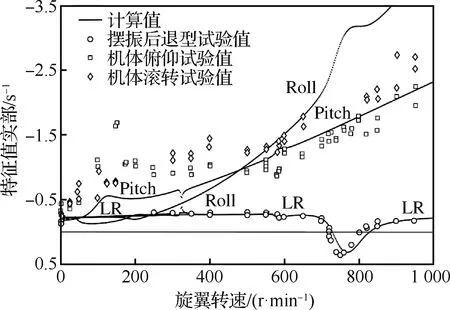
图4 Bousman旋翼/机体耦合试验配置1的系统各模态特征值实部随旋翼转速变化

3 算例重型直升机的飞行特性

使用建立的模型分析重型直升机的飞行特性。由于重型直升机数据的缺乏，本文基于Dutton针对重型直升机的初步设计文件[21]，结合CH-54直升机的现有数据[22]和基于统计的直升机典型设计参数，同时使用均匀铰接梁和拼接梁的振型近似桨叶和机体的弯曲振型[23]，得到了40 t级的重型直升机的估计参数，其主要参数如表1所示。由于机体二阶弹性模态频率较高，因此只需要保留最低的桨叶一阶弹性变形和机体的一阶垂向和横向弯曲变形就满足分析需要。

表1 重型直升机的主要设计参数

由于建模时考虑了桨叶的摆振运动，而大吨位直升机通常使用铰接式旋翼结合液压摆振阻尼器[2]，不提供刚度，设置等效阻尼大小为105N·m·s/rad。Ormiston[24]指出，机体的转动惯量越大，旋翼/机体耦合动态特性越接近于孤立旋翼的动态特性，因此为了使该耦合特性更加明显，本文的算例直升机飞行状态为：直升机总重16 329.3 kg，滚转、俯仰、偏航和滚转偏航耦合转动惯量分别是46 639.8、189 813.2、159 307.5、11 659.9 kg·m2，重心在桨毂中心前面0.61 m，飞行高度为500 m，温度为15°，飞行状态为悬停状态。

使用多桨叶坐标变换的方法把周期变化的系统矩阵变成常系数，为了对比考虑桨叶和机身弹性影响，首先列出了悬停时各种桨叶和机体刚性/弹性情况的特征值，如表2所示。观察表2可以发现，桨叶和机体弹性对直升机刚体低频运动模态影响较小，但对比刚性机体和弹性机体的摆振前进型特征值可以发现，因为机体弯曲频率与摆振前进型的频率较为接近，而这两种运动都与桨毂处的纵向位移有关，因此二者存在耦合，从而降低摆振前进型的阻尼，增加机体弯曲变形的阻尼。

为了便于分析状态量之间的耦合关系，图5为重型直升机在悬停时的部分特征向量图，图中各标记对应的状态量分别为：桨叶摆振零阶系数变化率dL0；桨叶摆振一阶正弦和余弦系数变化率dLs1和dLc1；桨叶挥舞零阶系数变化率dF0；桨叶挥舞一阶正弦和余弦系数变化率dFs1和dFc1；机体垂向和横向弯曲变形广义速度dpfver和dpflat；桨叶弹性变形二阶正弦系数dPBLs2；机体滚转角速度p、机体俯仰角速度q和俯仰角θ。桨叶和机体弹性对直升机刚体低频运动模态影响较小，但对比刚性机体和弹性机体的摆振前进型特征值可以发现，因为机体弯曲频率与摆振前进型的频率较为接近，而这两种运动都与桨毂处的纵向位移有关，因此二者存在耦合，从而降低摆振前进型的阻尼，增加机体弯曲变形的阻尼。

观察图5(a)，旋翼摆振前进型模态特征向量中出现了dpfver，说明机体的垂向弯曲变形会影响摆振前进型的模态特征，这与根据表2中特征值对比得出的结论一致，但dpfver在整个特征向量中的占比较小，说明在悬停时该模态仍然是以摆振前进型为主，机体垂向弯曲变形只会带来非常有限的影响。

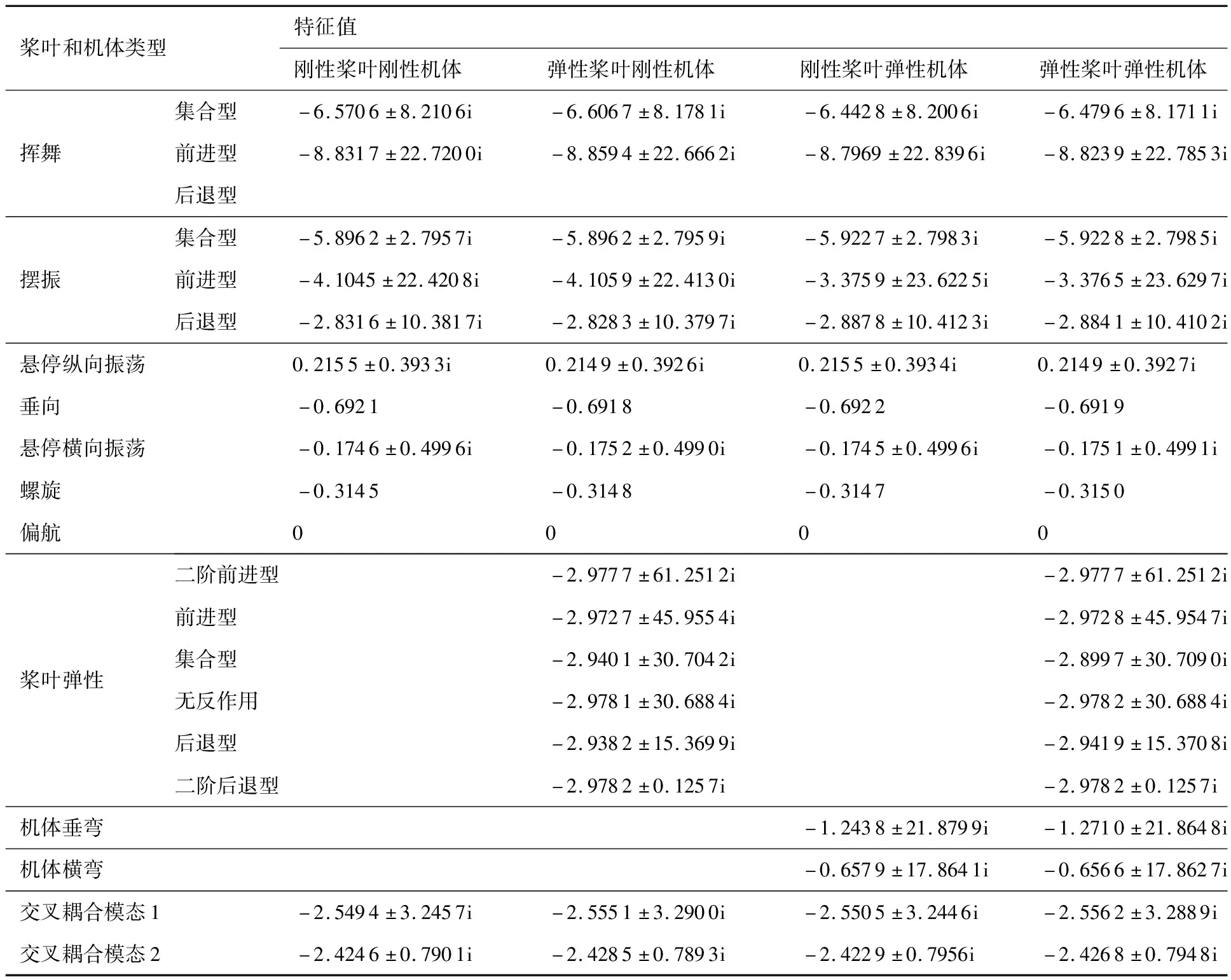
表2 不同桨叶和机体刚性/弹性情况的重型直升机悬停状态运动模态特征值

结合图5(b)可以发现，即使在计算模态振型时假设了机体垂向和横向弯曲变形是解耦的，但机体垂向弯曲模态中仍然会出现机体横向弯曲变形的广义速度，说明旋翼/机体的耦合作用会加强机体弯曲变形间的耦合。

对比图5(c)和图5(b)，横向弯曲变形模态的主要状态量dpflat的比重更大，说明横向弯曲变形与旋翼的耦合作用比垂向弯曲小，这一方面是因为垂向弯曲频率与旋翼模态频率比横向弯曲频率更加接近，另一方面是因为桨毂通过长的刚性旋翼轴连接在假设的机体梁上，机体垂向弯曲变形虽然只会导致旋翼轴与机体梁的连接点发生垂向运动，但由于旋翼轴的存在，垂向弯曲变形引起的连接点处的转角变化会反映在桨毂的纵向平移和俯仰运动上，而横向弯曲虽然会引起连接点以至桨毂的横向平移运动，但变形的转角变形不会体现在桨毂的平移中，且由于旋翼轴较长，垂向弯曲变形引起的桨毂运动量大小比横向弯曲变形更大，从而耦合效果越强。

此外，观察到图5(c)中出现了桨叶摆振零阶系数变化率dL0，但图5(b)中并没有出现，这意味着桨叶集合型摆振运动会与机体横向弯曲变形耦合，但几乎不与机体垂向弯曲变形耦合，这是因为横向弯曲变形的转角运动虽然不会引起连接点以至桨毂的横向平移运动，但却会引起桨毂的扭转运动，这与桨叶集合型摆振带来的旋翼扭矩变化引起的运动一致，从而导致两个模态的耦合。

观察图5(d)，本文保留的桨叶一阶弯曲变形是挥舞平面内的弯曲变形，该变形会导致桨叶质心在挥舞方向上的垂向运动，从而图中的桨叶弯曲变形的集合型会对桨毂作用垂向周期力，这与集合型挥舞对桨毂的作用力类似，而机体垂向变形又导致桨毂的垂向运动，从而三者间存在耦合关系。

图5(e)和图5(f)对应的交叉耦合模态1和2意味着悬停时，旋翼挥舞后退型、摆振集合型以及机体滚转和俯仰运动模态存在相互耦合。交叉耦合模态1主要由机体滚转角速度p、挥舞一阶正弦系数dFs1和挥舞一阶余弦系数dFc1构成，因此该运动模态的主要表现形式为机体的滚转运动和旋翼挥舞后退型的陀螺运动耦合的周期运动。交叉耦合模态2主要由机体的滚转角速度p、俯仰角速度q和挥舞一阶正弦系数dFs1构成，且以俯仰角速度为主导，挥舞一阶正弦系数dFs1的宏观表现为桨尖轨迹平面的侧倒，因此该模态主要表现为机体的俯仰和桨盘侧倒的耦合运动。

图5 重型直升机悬停状态的特征向量图

4 算例重型直升机的空中共振稳定性

通过第3节的分析可以得出，重型直升机空中共振的稳定性主要与机体弹性模态频率和阻尼、摆振运动频率和减摆器阻尼有关。由于液压减摆器不提供刚度，因此铰外伸量就成为了决定摆振运动频率的唯一参数，但本文估计的重型直升机模型参数对应的铰外伸量已经能够保证小重量悬停情况下摆振后退型频率远离旋翼转速。由于大吨位直升机通常采用液压减摆器，在空中飞行时需要开启减压阀以降低载荷，但同时减摆器的阻尼也会随着减压阀的开启而下降，所以确定减压后减摆器的有效阻尼要求就成为了直升机设计时避免空中共振的一个关键问题。因此只需要讨论在当前飞行状态下的减摆器有效阻尼需求。

空中共振的稳定性通常采用关键转速范围内的摆振后退型模态的阻尼来评估。胡国才[25]和王波[26]等建立了黏弹减摆器的非线性模型并研究了对空中共振的影响。薛海峰等[27]针对直升机在前飞状态下的空中共振各自由度之间的相互作用关系进行了研究，揭示了空中共振的物理本质。

本文为了确定避免空中共振所需要的最低的减摆器有效阻尼，由于机体模态最有可能与摆振前进型耦合，将机体垂向弯曲频率调节为24.8 rad/s，与1/rev旋翼转速下的摆振前进型频率相一致。图6是不同减摆器阻尼下，0.9～1.1倍转速区的空中共振关键模态的频率和阻尼，其中LR2表示桨叶二阶摆振更低频率的周期型模态；VertBend表示机体垂向弯曲模态。

观察图6(a)的频率变化曲线可以发现，频率基本不随摆振阻尼变化而变化，在超过1/rev转速时，机体垂向弯曲模态VertBend、摆振前进型LP和桨叶二阶摆振更低频率的周期型模态LR2三者出现耦合，导致机VertBend模态频率降低约2 rad/s，LP频率增加约2 rad/s，但LR2的频率不受耦合影响。

观察图6(b)可以发现，摆振阻尼对特征根的阻尼影响很大，当等效阻尼小于约5 000 N·m·s/rad时，摆振后退型LR是不稳定的，应当避免减压后的液压减摆器阻尼过小。