湍流燃烧机理和调控的活性子空间分析方法
2022-01-10王娜娜解青苏星宇任祝寅
王娜娜,解青,苏星宇,任祝寅,,*
1.清华大学 航空发动机研究院,北京 100084 2.清华大学 燃烧能源中心,北京 100084
湍流燃烧是航空发动机、冲压发动机、组合发动机、内燃机等动力装置工作的核心能量转换过程,燃烧组织的好坏直接关系到发动机的寿命、效率、污染物排放等[1-2]。而发动机湍流燃烧过程十分复杂,包括湍流、雾化/蒸发、辐射等多物理过程以及和化学反应的强耦合,具有非定常、多尺度的特征。目前随着更严格的高效、低排放等要求[3],湍流燃烧开始趋于近极限燃烧组织[4-5],亟需在稳定可控燃烧方面取得突破。这就需要进一步加深对湍流燃烧机理的认识,实现流动和化学反应的有效匹配和调控。对于该问题,数值仿真是当前重要的研究手段之一[6-7],从而支撑航空发动机的自主研发,仿真技术体现了一个国家的高端装备研发水平[8]。
然而,数值模拟中的湍流模型、燃烧模型和化学反应动力学模型等均涉及大量模型参数,这些参数可能具有很大的不确定性。以化学反应动力学为例,从氢气到大分子碳氢燃料的反应机理由数十到近千步反应组成,而每步反应均有一定的不确定性,导致仅在化学反应动力学模型中,就存在海量的不确定性参数[9-11]。这些模型参数的不确定性将导致仿真结果存在不确定性[12]。随计算机技术的发展、数值模拟研究方法重要性的提升,湍流燃烧模拟的不确定性分析在国内国际上得到了越来越多的关注[13]。2014年,美国NASA经过大量调研形成了一份综合分析报告[14],对计算流体动力学(Computational Fluid Dynamics, CFD)所涉及的技术到2030年时的需求及能力做了分析和预测。其中,针对不确定性分析单独给出了发展时间轴,预测在2025年之前需要实现不确定性在CFD中的传递。湍流燃烧模拟的模型不确定性来自于模型假设自身的不确定性以及模型参数的不确定性,前者可称为模型格式不确定性,Mueller和Raman[15]在这方面开展了大量工作,探究了小火焰燃烧模型不确定性在湍流燃烧模拟中的传递。本文则主要综述包含模型参数在内的输入参数不确定性在湍流燃烧中的传递。输入参数的不确定性分析可以得到各部分模型参数以及初始/边界条件不确定性的传递规律和参数敏感性,揭示湍流燃烧的主控物理机制,有助于量化数值仿真精度,提高航空发动机的设计和优化水平,尤其对近极限条件下如高温升航空发动机、超声速冲压发动机的设计具有重要意义。
湍流燃烧的输入参数空间通常包含化学反应动力学模型的反应常数、湍流模型、燃烧模型参数以及初始/边界条件。由于参数众多且单次多维湍流燃烧模拟计算成本高,使得湍流燃烧模拟的不确定性和敏感性分析面临的最大困难是“维度灾难”。因此,目前已有的研究集中在单一模型和少量模型参数的不确定性分析上。在化学反应动力学模型不确定性研究方面:学者利用灵敏度分析法降维,研究了化学反应速率常数不确定性对模型预测输出[16]、火焰传播速度[17]的影响,声振对层流预混火焰的火焰传递方程的影响[18],以及输运概率密度函数法湍流火焰模拟中单一基元反应对射流抬举高度和局部熄火/再燃的影响[19-22]。在湍流模型不确定性研究方面:学者基于多项式混沌展开,研究了Smagorinsky模型系数Cs和湍流普朗特数以及施密特数不确定性在非预混钝体稳定火焰大涡模拟(Large Eddy Simulation, LES)中的传递[13],Cs不确定性对湍动能预测影响[23],雷诺平均法(Reynolds-Averaged Navier Stokes, RANS)单方程和双方程模型系数层面的不确定性分析[24],模型系数对不同雷诺数下管道流动的影响[25],基于重心图法的模型格式层面的不确定性分析[26-27],以及在高速射流[28]、边界层分离[29]等问题中的应用。在燃烧模型不确定性研究方面:学者研究了小火焰模型不确定性在Sandia D火焰LES中的传递[30],进一步,采用随机搭配法研究了Delft III射流火焰上游温度不确定性对下游碳烟生成预测的影响[31],以及湍流燃烧模型格式不确定性对混合分数、温度分布以及一氧化碳生成的影响[15]。
然而仅考虑单一模型的不确定性无法量化多物理耦合下不确定性传递规律、难以表征不同物理过程中的主控因素。同时将化学动力学模型、湍流模型、燃烧模型以及初始/边界条件纳入不确定性研究中,可以从全局敏感性的角度分析输入参数对湍流燃烧目标量影响的内在物理机制,是当前一个重要研究方向。开展考虑多模型和初始/边界条件的湍流燃烧不确定性研究的关键是有效的海量输入参数降维方法。
近几年,Constantine等[32-33]提出了活性子空间(Active Subspace, AS)降维方法,该方法基于梯度的偏协方差矩阵特征分解,得到活跃特征方向,构建输入参数低维子空间,利用输入参数在该子空间的投影得到活跃变量,降低输入参数维度。该方法和其他常用敏感性降维方法的区别在于,敏感性分析保留的是影响较大的输入参数,而子空间分析保留的是影响较大的输入参数空间中的方向,这些方向是参数自身的线性组合,从而实现最大程度降维的同时保证精度。同时,活跃方向向量的分量值提供了目标量相对于输入参数的全局敏感性信息[34]。AS方法和其他常用降维方法如主成分分析(Principle Component Analysis, PCA)法均是对空间进行基的变换,识别重要方向,以达到降维的目的。但是两者仍有本质区别:前者得到的重要方向上映射的梯度最大,而后者分析中,沿重要方向数据的方差最大。也就是说AS分析对象为高维映射,而PCA分析对象为数据集;前者可得到低维响应面或预测模型,后者的目的则是实现对物理系统的低维描述。在燃烧领域的研究中,PCA被广泛用来识别化学反应系统的低维流形[35]、重构组分空间[36]以降低反应系统维度,并在后续燃烧问题求解中只对少数个主成分(Principle Components, PCs)求解输运方程[37-40],可极大地减少LES等湍流燃烧模拟中组分方程的个数[41-43]。
目前活性子空间方法在动力装置的机理分析和优化方面已有了成功应用。Constantine等[44]采用活性子空间方法将七维运转参数降为一维,研究了它们对HyShot II冲压发动机性能的影响。最近,Constantine等进一步将活性子空间方法应用在了设计方法发展[45]、翼型设计[46]、涡轮叶片设计[47]、以及高超声速模拟不确定性分析[48]中。Magri等[49]采用该方法分析了双环形燃烧器的热声稳定的不确定性,Guan等利用活性子空间构造了碳氢燃料辛烷值[50]和标准生成焓[51]的预测模型,并且将该方法应用在了可变正时汽油机的换气策略标定中[52]。
在湍流燃烧控制机理和模拟不确定性量化方面,Ji等首次将该方法应用在了化学反应动力学模型不确定性在自着火、层流火焰[53]和湍流火焰[54]模拟中的传递研究中,他们在零维燃烧模拟和湍流燃烧模拟中均得到了反应速率常数的低维子空间。Vohra等[55]将速率常数、活化能以及初始状态均考虑到输入参数空间中,对H2/O2反应得到了一维子空间。这些研究都实现了对海量化学动力学模型参数的降维。Wang等则率先发展了反应动力学、物理模型和边界条件参数连续降维方法,将动力学模型参数降维得到一维活性子空间后,联立湍流燃烧模型参数和边界条件参数再一次降维[56],得到了物理化学模型参数和边界条件不确定性的传递规律,揭示了超声速湍流射流火焰的主控物理机制[57]。活性子空间方法在湍流燃烧模拟的不确定性量化和主控机制分析方面有巨大的应用潜力,并且有助于后续的湍流燃烧调控分析。
本文将综述活性子空间方法在湍流燃烧模拟中已有的应用。首先简述活性子空间方法理论及针对湍流燃烧模拟发展的连续降维方法。然后介绍动力学参数、物理模型参数以及边界条件不确定性在燃烧模拟中传递的典型应用,以及研究得到的湍流燃烧机理。并进一步讨论展望基于活性子空间分析方法的湍流燃烧调控。
1 活性子空间方法
活性子空间方法可以在m维输入参数空间x∈m中识别出对应于目标量(Quantity of Interest, QoI)即输出量f(x)的低维结构,沿该低维方向f对x的梯度最大。通过对f(x)梯度的协方差矩阵做特征分解,可以得到输入空间的活性子空间:
(1)
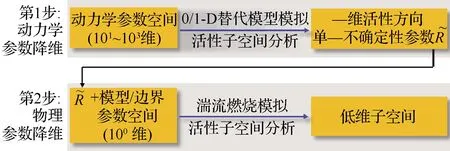
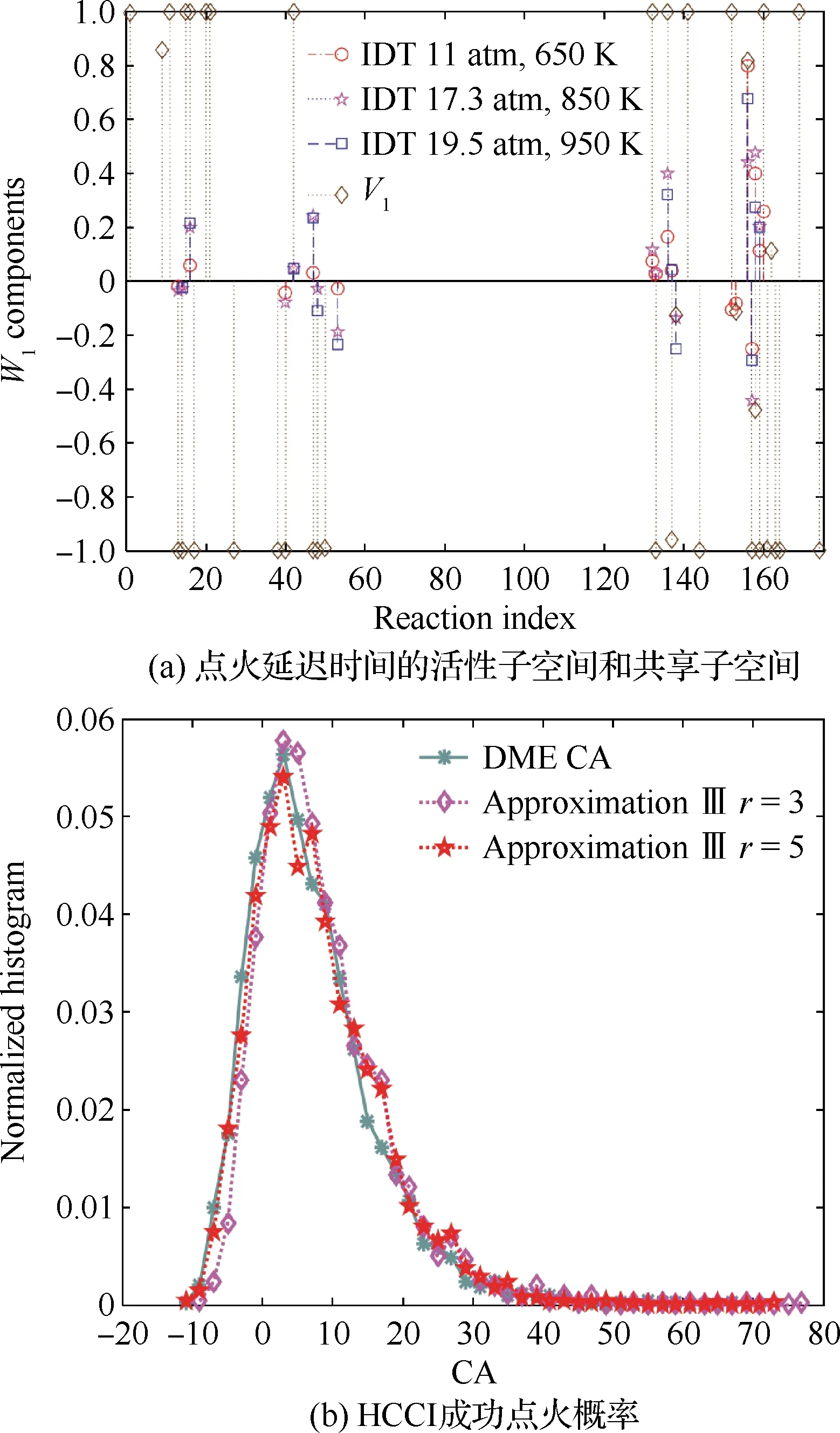
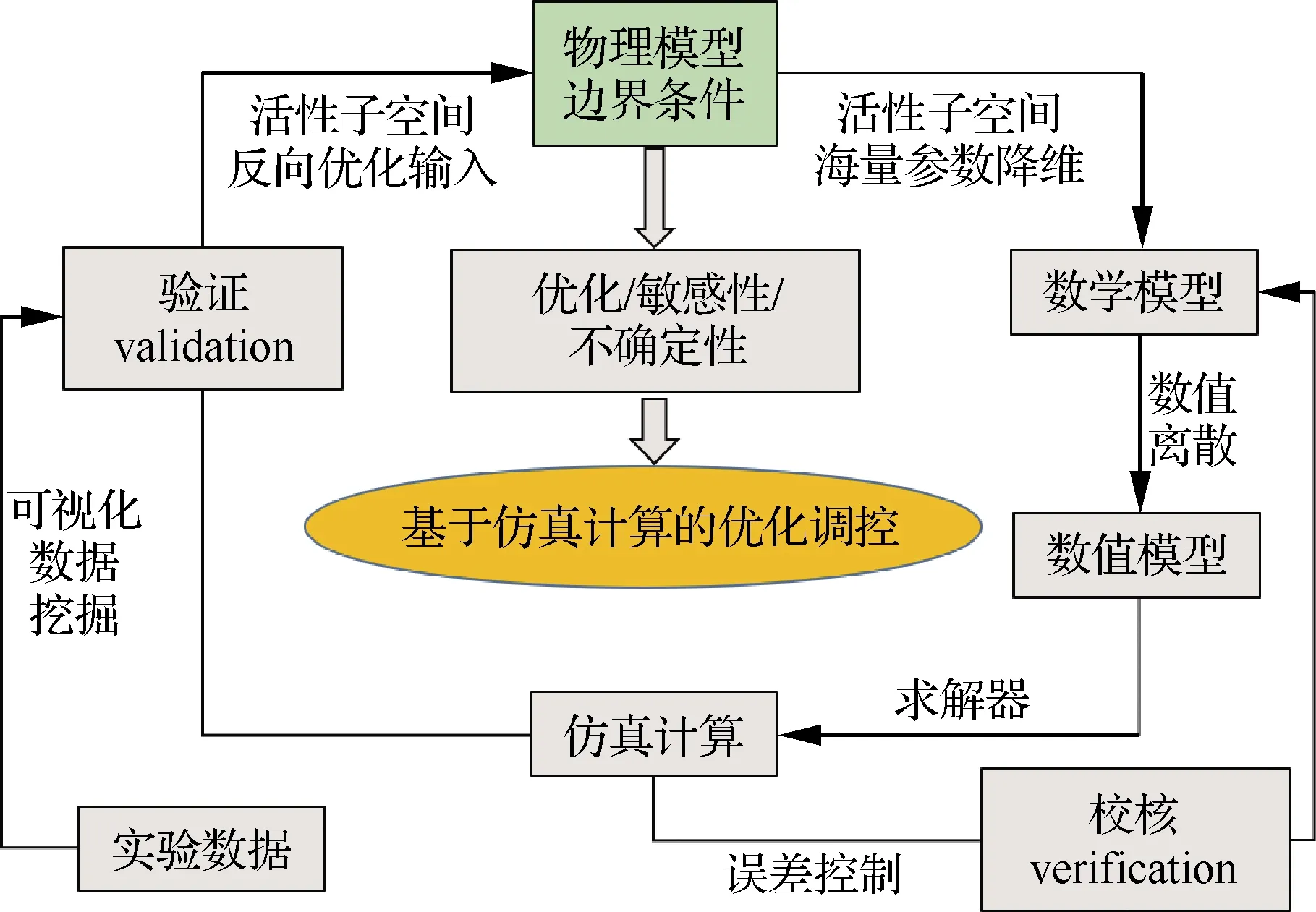
式中:π为输入参数的联合概率密度函数(Probability Density Function, PDF);C为对称半正定矩阵;W=[w1,w2,…,wm]为特征向量矩阵;Λ=diag(λ1,λ2,…,λm)为对应特征值组成的对角矩阵;其中λ1,λ2,…,λm从大到小降次排列,如果特征值λn远大于λn+1,即λn≫λn+1,n 图1 活性子空间分析中基变换以及响应面构建示意图 如果在仿真计算中可以直接得到映射f的梯度,那么,活性子空间可通过如下步骤在输入空间中的随机采样计算得到: 1)根据输入参数x∈m的概率密度分布π(x),在输入空间采M个样本{x(1),x(2),…,x(M)}。 3)估算矩阵C: 5)根据特征值的大小将特征值矩阵和特征向量矩阵分块: (2) (3) 接着对C进行特征分解,进行后续活性子空间分析。目前有限差分、全局线性拟合以及全局二次拟合均在实际中有了成功应用,表1总结了3种方法需要的样本数以及应用的文献[59-60],其中,α为取样系数,β为期望获得的子空间最大维度。 表1 梯度近似方法 以上讨论的为针对单一目标量的活性子空间,对于多目标量,Ji等[53]发展了共享活性子空间方法。假设对于d个目标量,映射fi可以完全降维到其一维活跃向量ui所展成的一维活性子空间中(i=1,2,…,d),即 (4) (5) 若对于i=1,2,…,d式(5)均成立,则v即为d个目标量的共享子空间。经过对v的求解发现,共享子空间是单一目标量子空间的线性组合。对于实际燃烧问题,由于物理过程的复杂性,在构建多目标量的共享子空间时,可增加每个单一目标量的活性子空间维度,以囊括更多的物理过程,提高共享子空间中对原空间映射近似的准确性。详细推导以及高维活性子空间的共享子空间方法可参见Ji等[53]文献。获得共享子空间后,在对多目标量的不确定性PDF量化和多目标量优化调控时,可以极大增加计算效率。对于多目标量优化,由于AS识别的是梯度变化最大的方向,并以该方向为基构建子空间,因此即使目标间存在矛盾性关系也不影响共享子空间的建立,但会体现在不同目标量在该子空间中响应面不同上。在进行后续的多目标优化调控时,则需根据实际问题需求,进一步建立代价函数,通过极小化代价函数,对输入参数进行折中调控,达到多目标量优化的目的。 对于带有详细化学反应的湍流燃烧模拟,不确定性来自于模拟反应动力学的反应机理以及燃烧模型、湍流模型等物理模型和初始/边界条件。通常碳氢燃料的反应机理包含数十到数千个基元反应,考虑每个基元反应建模参数的不确定性,输入参数空间将达到数十到数千维。此时,即使采用活性子空间方法,所需的样本数即湍流燃烧模拟次数仍然巨大,在当前的计算资源下难以实现。因此,Wang等提出连续降维方法[56],如图2所示,利用零维或一维化学动力学模型作为替代模型,首先将动力学模型参数进行降维,降维后的活性动力学参数与物理模型参数组成新的输入空间再次降维,实现采用较小计算量完成湍流燃烧仿真不确定性分析和主控物理机制分析。以下对该方法进行简单阐述。 图2 连续降维方法示意图 第1步为反应动力学参数空间降维。首先,根据实际工况的湍流燃烧模拟提取出用于零维或一维替代模型模拟的初始条件,选取适当QoI替代湍流燃烧模拟中的真实QoI。此处,适当QoI对子空间分析的合理性将在3.1节中通过文献结论综述进一步说明。再次,利用子空间分析得到替代模型映射的活跃方向。最后,将原输入参数向量投影到活跃方向上,得到对应活跃变量,对于碳氢燃料来说,活跃变量的个数通常为1~5个[53],从而实现由数千维到个数维的动力学参数降维。 第2步为动力学和其他物理模型参数空间降维。首先,将第1步中得到的活跃变量与物理参数组成新的输入空间,此时该空间维度由于第1步的降维已较原输入空间有了极大程度的降低。再次,在降维空间中采少量样本进行湍流燃烧模拟,进行活性子空间分析,得到该降维空间的活性子空间。最后,在该子空间中构建低维响应面,进行不确定性量化计算,同时根据子空间分析目标量的主控物理机制。 对于复杂的燃烧问题,如燃气轮机燃烧室中的燃烧过程,在明确目标量的基础上,选择和目标量所涉及的主要物理过程一致的零维或一维模拟,作为替代模拟。在复杂燃烧过程的热力学状态时空演化中选取若干状态点作为替代模型的初始状态,分别求解不同状态下的活性子空间。最后结合共享子空间方法,得到上述子空间的共享子空间,以及对应的动力学活跃变量,用于后续动力学-物理模型参数降维。 本节首先综述了化学动力学参数不确定性的活性子空间分析;接着,综述了输入参数拓展到物理模型常数和边界条件的情况,并且简明阐述了文献中分析得到的湍流燃烧机理。另外,综述了活性子空间方法在模型燃烧系统的性能预测中的应用。最后,讨论了基于活性子空间分析方法的湍流燃烧调控。 Ji等[54]针对湍流射流Cabra火焰[61]开展了活性子空间分析,研究了动力学参数的不确定性在湍流燃烧模拟中的传递。射流火焰的模拟结果如图3所示,目标量为火焰推举高度H。在他们的工作中,采用了氢气/空气反应机理Li-2004[62]机理以模拟氢气氧化的反应动力学过程。将基元反应的速率常数作为不确定性输入参数,进一步依据Sheen等[63]的研究将速率常数定量为相互独立的对数正态分布: 图3 Cabra湍流射流火焰OH质量分数云图仿真结果[54] (6) 式中:kr为第r个基元反应的速率常数;kr0为其对应的名义值;Fr为其对应的不确定性因子[64],各个反应所对应的Fr见表2。 表2 基元反应所对应的不确定性因子 通过分析84个湍流燃烧模拟样本数据,得到了21维动力学参数空间的活性子空间,对应活跃方向的分量如图4中三角符号所示。由该分量得到的全局敏感性信息可以看出,链分支反应R1和R11对火焰推举高度的影响最为显著,其次,反应R9的影响也较为显著,但是其分量符号与R1和R11相反,原因是该反应降低了混合气的活性从而抑制了自着火的发生。之后,他们在该一维子空间中利用多项式拟合构建了一维响应面,最后通过50 000个样本点得到了火焰推举高度的不确定性概率密度分布。 此外,Ji等在他们的工作中探究了采用零维自着火模拟计算子空间,该模拟的工况为Cabra射流火焰模拟的参考工况,目标量为点火延迟时间(Ignition Delay Time, IDT)。得到的动力学参数的活性子空间如图4中的圆圈符号和正方形符号所示,两者分别为采用有限差分和全局线性拟合得到的结果。通过对比采用湍流燃烧模拟和零维自着火模拟得到的活跃向量方向,Ji等认为,实际湍流燃烧中扩散作用使得火焰稳定区域前缘的HO2浓度较高,而零维自着火模拟中不能体现扩散作用,所以R11和R13在零维模拟的影响小于其在湍流燃烧模拟中的影响。但总体来说,两者最敏感的基元反应均是R1、R9和R11,并且,两者的活跃方向向量的内积为0.91,说明方向几乎一致。 图4 Cabra火焰推举高度的活跃方向分量[54] 因此,Ji等认为,如果低成本替代模拟和湍流燃烧模拟的主控物理过程一致,那么,可以采用替代模型初步探究子空间的维度以及活跃方向向量的主控分量,从而确定敏感度较大的输入参数。进一步,可以在湍流燃烧模拟中将不敏感的输入参数剔除,从而减少样本个数,减少活性子空间分析的计算成本[54]。Wang等[56]同样开展了替代模型和对应湍流燃烧模拟的活性子空间分析,通过两者得到的活跃方向向量的内积为0.97,表3总结了文献中采用替代模型和湍流燃烧模拟得到的子空间的相近程度。该结果进一步说明对于湍流燃烧模拟中动力学参数部分,可以采用具有相同主控物理过程的低成本替代模拟进行确定,从而降低湍流燃烧模拟的样本数和计算成本,同时也说明了第2节中所阐述的连续降维方法的合理性。 表3 替代模拟和湍流燃烧模拟活跃方向内积 Wang等[56-57]采用连续降维方法分析了Burrows-Kurkov(B-K)超声速壁面射流火焰[65-66]的主控物理机制。火焰的温度云图如图5所示,其中L为火焰推举长度。图6展示了火焰推举长度对输入参数的敏感性,作者发现,动力学参数中反应R1、R3以及R9对火焰的点火起始位置影响最为显著,如圆圈符号所示,其中反应标号和表2中给出的一致。反应R1主导了火焰点火位置,这与Wu等[67]对B-K火焰的化学爆炸反应模态分析的结论一致,即他们研究发现,火焰稳定位置上游处的OH和H主导了化学爆炸混合层。 图5 B-K火焰温度云图仿真结果[56] 图6 B-K火焰推举长度的活跃方向向量分量[56] 当进一步将湍流模型和燃烧模型参数考虑在内时,此时的活跃方向分量展示了推举长度对动力学和物理模型参数的敏感性,以及物理模型参数的摄动动对关键反应的影响,如图6中三角符号所示。可以看出反应R1和湍流普朗特数(Prt)对推举长度的影响最显著,根据该子空间中响应面的单调递增[56]特性,可以进一步得出,R1的反应速率越快或湍流普朗特数越大则推举长度越小,这是因为R1反应速率的增加可以减短自着火时间,湍流普朗特数的增加则会减小当地的湍流热扩散,两者都将有利于氢气自着火的发生,从而使得推举长度减短。另外作者从输入空间参数摄动相互影响的角度得出,当物理模型的参数为不确定性输入参数时,动力学模型参数中H2/O2链分支反应的敏感性被略微抑制,而HO2生成和消耗反应的敏感性被一定程度增强,从而揭示了B-K火焰点火起始位置的主控过程以及他们之间的相互作用机制。 图7 活性子空间随壁面射流火焰流向的空间演化[57] Ji等[53]发展了基于活性子空间的共享子空间方法,用来解决多目标量的活性子空间问题。他们用该方法探究了内燃机甲烷和二甲醚(DME)均质压缩点火(Homogeneous Charge Compression Ignition, HCCI)的点火曲轴转角和点火失败概率。在该研究中,采用零维HCCI模型模拟的燃烧系统来近似三维湍流燃烧模拟。HCCI的子空间由点火过程中6个热力学状态下的定容自着火模拟训练得到,其中对于DME,该6个热力学状态包含了由低温化学带来的两级着火和负温度系数(Negative Temperature Coefficient, NTC)的状态点。以下简要阐述DME点火过程主控物理机制的活性子空间分析。 图8(a)展示了低温(650 K)、中等温度(850 K)以及高温(950 K)HCCI点火过程中参考状态下的点火延迟时间的第1个活跃方向向量分量。其中低温工况包含了两级着火,高温工况为一级着火过程。可以看出,不同温度下IDT的活跃方向具有显著区别。650 K工况下IDT对高标号反应相对敏感,例如氢原子提取反应以及之后的低温反应路径所涉及的反应。而850和950 K工况下IDT对低标号反应也相对敏感,对应于小分子反应,该现象和NTC现象一致,即随温度的升高,与HO2相关的基元反应的重要性显著增加。进一步由参考工况下的子空间训练得到了共享子空间用于HCCI的点火成功概率分析,如图8(a)中菱形符号所示,得出的点火成功概率随曲轴转角的关系如图8(b)所示,点火失败概率为37.9%。 图8 点火延迟时间的活性子空间和共享子空间以及HCCI成功点火概率[53] Zhang等[68]对振荡燃烧神经网络模型系统开展了活性子空间分析。通过非稳态良好搅拌器(Perfect Stirred Reactor, PSR)模型模拟振荡燃烧过程,得到了从混合气摩尔分数、当量比、热值、流率波动等8个输入参数到目标量最高温度的映射。他们得到了目标量的一维输入子空间,通过分析对应活跃方向向量分量发现,增加混合气中燃料质量分数尤其是CO质量分数将使最高温度显著增加从而提升燃烧系统的稳定性。同时当量比的影响也较大,在化学计量当量比附近减少当量比同样会带来最大温度的提升。进一步,他们将子空间所对应的活跃变量替代原有的8个输入变量,显著简化了神经网络预测模型的结构形式,如图9(a)所示。简化后的神经网络模型的预测结果如图9(b)中双点划线所示,与原模型的预测值(蓝色点划线所示)几乎一致。但是,神经网络的训练时间缩短了73%,单步预测时间加快了3倍。 图9 振荡燃烧神经网络和温度预测曲线[68] Briones等[69]采用活性子空间方法探究了小型化凹腔燃烧室几何参数对燃烧的影响,共包含空气入口参数、凹腔长度以及喷油位置15个几何参数。在他们的分析中,没有得到目标量(最大和平均温度)所对应的低维活性子空间,但是,通过和Spearman敏感性分析得到的结果对比,发现活性子空间分析中最大特征值所对应的特征向量分量得到的参数的敏感性和Spearman秩相关系数得到的敏感性一致,说明在该情况下即使目标量不存在低维的输入参数子空间,活性子空间分析中最大特征值对应的特征向量仍能够用来做全局敏感性分析。 从以上综述的研究进展可以看出,当前湍流燃烧模拟的活性子空间分析多集中在主控物理过程分析和正向不确定性的量化上,这些分析可以揭示特定目标量的的主控机制,从而探究湍流燃烧机理。但是,更进一步需要实现对湍流燃烧的调控,这就需要建模-计算-验证形成闭环,如图10所示。循环的右半侧从物理模型到仿真计算结果,其中由模型和边界条件带来的不确定性即可通过活性子空间对海量参数的降维实现,同时如上文综述的研究来探究物理问题的主控机制。循环的左半侧则为,从仿真计算结果结合实验数据或设计目标,反向调整输入参数,实现对目标量的调控。 图10 基于仿真计算的优化调控循环 在目标量调控的活性子空间研究方面,Constantine等[44]在对HyShot II超燃冲压发动机仿真研究中,利用构建的一维单调响应面,确定了满足安全运行所对应的目标量约束的操作参数范围。如果实验数据或设计目标是关于目标量的概率分布,此时参数调控问题为反向概率问题,即贝叶斯问题,在采用马尔科夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)采样时可以引入活性子空间方法,使采样空间减缩到后验概率密度空间的子空间中[33],从而提高反向参数调整的效率。湍流燃烧模拟反向问题可以得到满足目标要求的输入参数分布从而实现对湍流燃烧的调控。 活性子空间分析在湍流燃烧模拟中的应用,实现了对包括动力学模型参数、湍流燃烧模型以及边界条件参数等海量输入参数的降维,得到了复杂物理化学过程中的主控机制,有助于揭示湍流燃烧的机理,进一步实现对湍流燃烧的调控。主要工作和结论包括: 1)阐述了活性子空间方法和针对包含化学反应机理的湍流燃烧模拟的连续降维方法。该方法在对化学动力学参数降维中采用了替代模型,极大降低了所需湍流燃烧模拟次数。 2)总结了活性子空间方法和连续降维方法在Cabra火焰和B-K壁面射流火焰中的应用。揭示了湍流射流火焰中的关键化学反应以及主控物理过程的空间演化。 3)总结了模型燃烧系统的活性子空间分析,包括零维HCCI点火系统化学动力学主控机制分析、非稳态PSR振荡燃烧的神经网络系统的输入参数降维,以及凹腔燃烧室几何对湍流燃烧的影响。 4)对于湍流燃烧调控的活性子空间分析,可根据子空间中的低维响应面对输入参数进行调整,从而调控湍流燃烧过程。另外,可以通过在活性子空间中采用MCMC采样,开展反向概率研究,实现湍流燃烧调控。




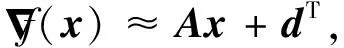

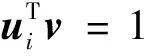
2 湍流燃烧仿真不确定性和主控机制分析
3 结果综述和展望讨论
3.1 化学动力学参数不确定性




3.2 化学动力学-物理模型参数不确定性


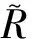

3.3 模型燃烧系统燃烧性能预测

3.4 讨 论
4 结 论
