非牛顿流体射流雾化特性研究进展

杨立军，刘陆昊，富庆飞

北京航空航天大学 宇航学院，北京 102206

液体射流这一物理过程在众多工业领域中都有着重要的应用。例如在燃油锅炉、内燃机、燃气轮机、吸气式发动机和火箭发动机等动力装置中，液体燃料在进行燃烧前都要通过喷嘴以液体射流喷射的方式进行雾化。因此，研究液体射流雾化的物理过程，对优化相关设备的设计是至关重要的。近年来，以凝胶推进剂为代表的非牛顿流体作为燃料在冲压发动机和火箭发动机上具有越来越广泛的应用前景。从流体的物理属性上来看，凝胶推进剂同时具有固体推进剂储存时间长以及液体推进剂推力易调节等优点，是一种极具前景的新型推进剂。然而，凝胶推进剂由于其自身的高黏度和非线性的流变特性，在实际使用中的雾化效果并不理想。因此，需要通过对非牛顿流体射流的雾化过程进行详细研究，以确定在整个过程中液体射流所经历的物理现象，同时就相关现象进行讨论与分析。

非牛顿流体射流在离开喷嘴后，首先会进行初次雾化(Primary Atomization)过程。在初次雾化过程中，液体射流表面会因喷嘴出口的毛刺和气液剪切作用而产生小扰动。随着液体射流在空间上的不断发展，小振幅的扰动会逐渐增长放大，当扰动的振幅与液体射流的半径大小在同一数量级时，液体射流将无法保持自身的形状而发生破裂，并形成大量的液丝和液滴。对于牛顿流体，其在初次雾化过程结束时会产生大量的液丝和液滴。随着液体黏度的不断升高，所产生液丝的比重会不断提高。对于非牛顿流体，因自身具有的弹性效应，在初次雾化的过程中通常会经历较大形变的拉伸流动，进而在初次雾化过程中产生拉丝等物理现象；具有相同剪切黏度性质的非牛顿流体，因其不同的流变性质，也会呈现不同的雾滴平均尺寸和尺寸分布。与此同时，与牛顿流体射流的初次雾化过程相比，非牛顿流体射流的破碎时间也会显著地增长。现有研究表明，在气液交界面小扰动发展的初始阶段，可以利用摄动法并结合稳定性分析的手段对扰动波的发展过程进行理论预测，得到扰动波增长率的理论表达式，并研究不同物理参数对扰动波发展的影响。随着扰动振幅的不断增大，当液体射流接近于破裂点时，线性稳定性分析手段将不再适用。此时，需要通过非线性稳定性分析与实验观测相结合的手段对液体射流的破碎过程进行描述，以得到液体射流破碎长度等描述射流初次雾化特性的关键参数。

当流体射流发生破碎后，会形成多种尺寸的液滴。液滴在高速气流的作用下会进一步地发生变形与破碎，最终形成数量众多的小液滴，这一过程被称为液滴的二次雾化(Secondary Atomization)。有关二次雾化的研究内容也是流体力学中的重要组成部分。对于牛顿流体，液滴在气流中受到气动力、表面张力以及黏性力的共同作用会使得液滴发生破碎，形成大量尺寸更小的液滴，喷雾场内液滴的平均粒径较小。对于非牛顿流体，液滴在气流中的二次雾化过程会受到自身的流变性质的影响。液滴在破碎过程中，相较于牛顿流体液滴将产生网状等不同结构，进一步导致其破碎模态发生改变；同时，液滴二次雾化的变形破碎特性，如总破碎时间等，同样会因非牛顿性质的考虑而发生变化。由于相关理论的缺乏，在现阶段的研究中通常可通过实验观测的方法对液滴二次雾化中有关的特性参数进行测量。对二次雾化过程中所涉及的物理过程的归纳分析，类比到非牛顿流体射流初次雾化的进程中，以预测非牛顿流体射流初次雾化结束后，喷雾场内液滴的平均粒径，所建立的预测模型被称为液体射流的雾化模型(Atomization Model)。利用雾化模型对喷雾场内的平均粒径进行预测，可以减少喷嘴实验的次数与时间，以更低的成本得到液滴平均粒径随不同物理参数的变化规律。

总之，非牛顿流体射流的初次雾化过程以及在初次雾化结束后所产生液丝和液滴的二次雾化过程共同组成了非牛顿流体射流离开喷嘴出口后的整个雾化过程，初次雾化与二次雾化过程的示意图如图1所示[1]。本文将对现阶段非牛顿流体射流的初次雾化过程中有关扰动波发展的理论分析及实验结论、非牛顿流体液滴二次雾化的实验结果及雾化模型在预测喷雾场平均粒径上的应用进行总结，并对未来可能的研究方向与研究内容进行展望。

图1 液体射流初次及二次雾化过程[1]

1 非牛顿流体射流初次雾化特性研究

当液体射流从喷嘴出口喷出后，在流体内部或外界扰动的作用下，射流表面会形成初始小扰动。实验表明，射流表面所产生的扰动波及其后续的发展是造成液体射流失稳的主要原因。因此，根据这一基本原理，可以利用摄动理论分析液体射流失稳破裂的过程，从而进一步确定液体射流的破裂长度、扰动波长、扰动增长率等物理特性参数。因此，液体射流的稳定性这一理论问题不仅是流体力学领域内的经典问题，同时对现代喷雾燃烧技术的发展起到了极为重要的作用。这一理论的正确性可以通过进一步的雾化实验进行验证。接下来，本部分将对非牛顿流体射流的破碎及雾化的物理过程进行总结，得到不同种类和射流形式的非牛顿液体射流初次雾化理论和实验结果。对相关结果进行分析，以证明稳定性理论的有效性。

首先对在不同条件下非牛顿液体射流稳定性问题中有关的结论和研究进展进行综述。接下来，对不同种类非牛顿流体射流的有关实验进行总结，同时对未来可能的研究方向进行展望。

1.1 非牛顿流体射流初次雾化理论

通过对非牛顿流体射流初次雾化的物理过程进行理论研究，可得到射流表面扰动波的发展规律，得到表面扰动波增长率、表面扰动波形等特性参数，进一步可以预测射流破碎长度等雾化参数随流动参数的变化规律。对于非牛顿流体射流的理论研究，现有的研究主要是利用摄动法，对描述流体运动的运动方程和动量方程等进行线性或弱非线性展开，同时结合相关运动学和动力学边界条件，最终得到描述表面扰动波增长率与波数关系的色散方程(Dispersion Equation)。随后，对所得到的色散方程进行无量纲化，使所得的结论具有普适性。在进行参数分析时，改变流动系统中的各个无量纲参数，以得到不同流动参数对表面不稳定波增长率的影响。

接下来，将对黏弹性流体以及幂律流体这2种常见的非牛顿流体射流的相关射流稳定性理论研究成果进行综述，并分析得到控制液体射流破碎的主要因素。

1.1.1 幂律流体射流线性稳定性理论

幂律流体(Power-Law Fluid)是一种在受到剪切作用后，切应力与切应变之间满足幂指数关系的流体。如果对幂律流体进行进一步地划分，可以将其分为剪切变稠和剪切变稀2种流体。在常见的凝胶推进剂或燃料中，所使用的流体大多数属于剪切变稀类型的幂律流体。

根据现有研究可以发现，平面液膜和圆柱射流是从喷嘴出口喷出后液体射流的主要组织形式。因此，不同学者对幂律平面液膜和圆柱射流的稳定性问题进行了理论研究，并得到了一些重要结论。Yang等[2-3]利用小扰动假设，分析得到了正弦模式(非轴对称模式)与曲张模式(轴对称模式)下幂律圆柱射流的失稳过程，并推导得到有关的色散方程。随后，分析了表面张力、幂律指数等扰动参数以及气体边界层、速度型效应对液体射流不稳定参数(最大增长率、主导波数等)的影响。研究发现，液体射流的最大增长率和主导波数会随着表面张力的增大而减小；同时，会随着气液速度比、密度比的增大而增大。对于幂律流体，其非牛顿特性主要表现在流体的幂律指数和稠度系数上。Yang等[2-3]利用小扰动假设，分析得到了幂律圆柱、平面射流在发展过程中，幂律指数和稠度系数对射流稳定性的影响。可以发现，幂律流体的稠度系数K对射流的失稳具有双重作用。当K大于临界值时，增大稠度系数K会促进液膜的失稳；当K小于临界值时，增大稠度系数K会抑制液膜的失稳。与此同时，主导波数也会随着稠度系数的增大而发生变化。稠度系数K对扰动增长率的影响如图2所示[3]。同时，还研究了幂律指数对液体射流失稳的影响，所得的结果如图3所示[3]。

图2 稠度系数对幂律射流稳定性双重影响[3]

图3 幂律指数对幂律射流稳定性的影响[3]

可以发现，稠度系数对射流失稳的贡献是单调的。随着稠度系数的增大，射流的最大增长率在不断下降。然而，不同于稠度系数，主导波数几乎不随稠度系数的增大而发生变化。进一步说明，改变流体的幂律指数，并不会改变射流破碎后所形成的液滴尺寸。

Liu等[4]利用加权残差法从理论上研究了在黏性气体环境中幂律平面液膜在轴对称模式下的线性不稳定性。加权残差法的使用提高了幂律液膜在中性稳定区域附近对有关失稳特性预测的准确性，所得到的结果如图4所示[4]。这一点是传统的动量积分法无法实现的。此外，将理论计算所得到液膜表面波的波长与实验的测量结果进行对比，发现两者之间符合较好，进一步证明了现有理论的准确性。

图4 幂律指数对液体射流稳定性的影响[4]

根据现有关于幂律流体失稳的理论研究可以发现，无论是幂律平面射流还是圆柱射流的喷射形式，不同的来流参数均会对射流的失稳产生重要的影响。在未来的研究中，可以进一步考虑传热传质效应或含有表面活性剂幂律射流的失稳过程，并对相关问题进行线性稳定性分析，以得到更加符合实际物理过程的结论。

1.1.2 黏弹性流体射流线性稳定性理论

黏弹性流体(Viscoelastic Fluid)是一种同时具有固体弹性特性和液体黏性特性的一种流体。在描述这种流体时，需要同时结合弹性固体所满足的胡克定律与黏性流体所满足的牛顿内摩擦定律，本构方程即为描述非牛顿流体黏性与弹性特征的关系式。下面，对近年来本课题组有关黏弹性射流的失稳及破碎过程的理论分析进行综述。

Yang等[5]研究了在横向直流电场中黏弹性平面液膜和圆柱射流[6]的线性稳定性，在推导计算中得到了正弦模式与曲张模式2种不同的扰动发展模式。理论分析结果发现，在横向直流电场的作用下，黏弹性流体液膜要比牛顿流体液膜更加不稳定。在轴对称扰动模式下，带电黏弹性圆柱射流的扰动增长率要大于牛顿射流；在非轴对称扰动模式下，带电黏弹性圆柱射流的扰动增长率几乎与牛顿射流相等。增大韦伯数、雷诺数和电欧拉数会促进2种破碎模态下黏弹性射流的失稳过程，图5为弹性数El对黏弹性平面液膜失稳的影响。

图5 弹性数对黏弹性平面液膜失稳的影响[5]

然而，增大黏弹性流体的无量纲横向距离会抑制平面液膜的失稳。同时发现，弹性数的增大对液膜的失稳几乎不产生作用。因此，电场的总体效应是会促进黏弹性平面液膜的失稳。当射流两侧的速度不相等时，Yang等[7]发现当液膜上下两侧的气体速度差增大时，黏弹性平面液膜的不稳定性会增强。然而，平面液膜扰动的主导波数和不稳定区域几乎不随两侧气体的速度差而发生变化。此外，Tong等[8]发现，弹性数对平面液膜的失稳作用较为有限。然而，变形延迟时间会显著地增强气体对平面液膜的作用，并使得流体弹性对平面液膜的失稳表现出更加重要的作用。进一步发现，燃烧室中的气体旋流效应对射流的稳定性具有重要的影响。Yang等[9]和Tong等[10]对考虑旋流气体三维黏弹性流体射流的线性不稳定性进行了理论分析。结果表明，旋流气体效应、流体的变形延迟时间和流体的零剪切黏度对黏弹性射流的失稳起到了抑制作用，流体的弹性对射流的失稳起到了促进作用。进一步地研究表明，当旋流气体的强度较大时，非轴对称模式占优并主导射流的失稳过程。

此外，对于黏弹性流体，其流变参数主要表现在流体的应力松弛时间和变形延迟时间上。Yang等[5-6]研究了黏弹性圆柱和平面射流中黏弹性参数对射流稳定性的影响。理论分析的结果如图6所示[6]。结果表明，随着时间比λ(变形延迟时间与应力松弛时间之比)的增大，液体射流的最大增长率及主导波数均会下降。可以发现，应力松弛时间表征了射流内部所蕴含的弹性，弹性的增大会导致时间比的减小，最终促进射流的失稳过程。变形延迟时间表征了射流内部的黏性耗散效应，黏性耗散的增大会导致时间比的增大，最终抑制了射流的失稳过程。

图6 时间比对黏弹性液膜稳定性的影响[5]

在黏弹性流体实际的破碎过程中，未松弛的拉应力是其在离开喷嘴出口后所表现出的一种特有的物理属性，会对黏弹性流体的失稳和破碎产生重要的影响。Yang等[11]研究了在同轴气流条件下黏弹性圆环射流中未松弛拉应力对表面不稳定扰动波演化过程的影响。结果发现，考虑黏弹性流体内部的未松弛拉应力Te时，射流的扰动增长率会减小，理论分析结果如图7所示。其中，纵轴代表扰动波增长率Br，横轴代表扰动波波长。

图7 未松弛拉应力对液体圆环扰动最大增长率的影响[11]

此外可以发现，弹性数与奥内佐格数在考虑未松弛拉应力的前后会对射流的失稳会产生不同的影响。然而，无论是否考虑未松弛拉应力的影响，时间常数比、气液密度比以及气液速度比对射流的失稳所起到的效果是相似的。Tong等[12]研究了在电场作用下，存在未松弛轴向拉应力黏弹性液膜的稳定性问题。利用Oldroyd八参数模型描述了黏弹性流体的流变特性，发现未松弛轴向拉应力的存在会抑制液膜的失稳，降低电欧拉数也能够对液膜的失稳起到抑制作用。

Xie等[13]进一步地研究了在无黏气体环境中随空间位置衰减的未松弛拉应力对黏弹性液体射流空间不稳定性的影响。结果表明，沿空间衰减的未松弛拉应力对射流失稳的影响十分复杂，所表现出的性质主要取决于黏弹性射流的应力松弛时间。当应力松弛时间较短时，破碎长度会随未松弛拉应力的增大而略微增长；当应力松弛时间大于一临界值时，会使得流体射流具有更大的破碎长度。未松弛拉应力对流体射流失稳所表现出的双重效应主要是未松弛拉应力自身对射流所起到抑制失稳作用与其沿空间不断衰减所起到促进失稳作用两者相互竞争的结果。

在实际发动机工作过程中，传热传质效应对贴壁液膜的稳定性具有重要的影响。Tong等[14]考虑了二维黏弹性平面液膜在存在温度梯度气流中的热毛细稳定性问题。研究表明，当气液温度差足够大时，黏弹性液膜要比牛顿流体液膜更加稳定。说明了传热效应对液膜失稳的抑制作用，不同马兰戈尼数Ma和普朗特数Pr下扰动最大增长率的变化趋势如图8所示[14]。其中，纵轴代表扰动波增长率，横轴代表扰动波波长。

图8 传热效应对液膜扰动增长率的影响[14]

具体而言，传热效应会延缓液膜在大韦伯数条件下的失稳及破碎过程，变形延迟时间对液膜的失稳起到促进作用，还研究了热毛细不稳定和气动力不稳定两者之间的相对大小关系。Fu等[15]研究了传热传质效应对受限黏弹性圆环液膜在有黏气体环境中Kelvin-Helmholtz(K-H)不稳定性的影响，传热传质效应由一无量纲的气液界面上热传导与相变热之间比值来表征。结果表明，最大增长率与不稳定区域都会随着传热传质效应的增强而不断增大。

当液体射流离开喷嘴出口进入燃烧室后，燃烧室内振荡的速度及压力气体会对射流的失稳产生影响。近年来，Jia等[16]研究了在来流气体振荡条件下，黏弹性平面液膜的线性稳定性问题。在数学上应用了Floquet理论对有关方程进行了处理与简化。研究发现，当来流气体振荡时，会产生多个不稳定区域。这些区域被分为了K-H不稳定区域和参数不稳定区域，如图9所示[16]。

图9 气流来流速度振荡条件下所产生的K-H不稳定区域与参数不稳定区域[16]

在K-H不稳定区域，扰动波会以行波的形式进行增长。在参数不稳定区域，扰动波会以驻波的形式进行增长。当来流气体的振幅增加后，会导致这2种不稳定区域内扰动增长率的放大。同时发现，黏弹性液膜在不同区域内都表现出比牛顿液膜更强的稳定性。然而，零剪切黏度、应力松弛时间和变形延迟时间的变化对参数不稳定区域会产生更加显著的影响。此外，相比于K-H不稳定区域，参数不稳定区域内扰动的最大增长率对黏性耗散的敏感性更高，最终导致了不同稳定区域之间主导失稳因素的不断变化。

1.1.3 非牛顿流体射流弱非线性稳定性理论

通过以上的分析可以发现，线性稳定性分析在射流发展的初始阶段能够较好地描述其失稳特性。然而，线性稳定性由于只适用于小扰动的情况，在描述射流临近破碎的物理特征时，需要利用弱非线性稳定性分析的方法进行求解。

在线性稳定性的基础上，Wang等[17]进一步研究了在无黏气体中，存在初始正弦模式扰动的二维黏弹性平面液膜的弱非线性稳定性问题。研究结果表明，正弦模式扰动的二阶谐波为曲张模式，曲张模式的产生是造成液膜最终破碎的主要原因。在主导波数下，增大液体的弹性或降低液体的变形延迟时间都会提高扰动增长率和二阶谐波振幅并导致更短的破碎时间。此外，利用能量分析的方法研究了液膜发生失稳的主要机理，结果表明气动力的作用是导致其发生失稳的主要原因。

Xie等[18-19]利用弱非线性分析的方法研究了在无黏度且不可压的气体环境中，未松弛拉应力对黏弹性平面液膜稳定性的影响，图10为流体弹性数对液膜破碎时间的影响[18]。

图10 弹性数对液膜破碎时间的影响[18]

研究结果表明，未松弛拉应力的存在不仅显著地抑制了液膜的失稳，而且还会使得液体弹性数从抑制液膜失稳转变为促进液膜失稳。这一现象解释了实验中黏弹性效应对射流失稳的多重影响。此外，还研究了存在初始曲张扰动黏弹性平面液膜的弱非线性稳定性。理论推导的结果表明，液膜破碎时曲张模式扰动的二阶谐波仍为曲张模式，与一阶曲张模式的叠加效应导致了液膜的破裂，产生了由2个大尺寸液滴所连接的液丝结构。当液膜破碎后，其形状主要取决于一阶增长率、二阶增长率和二阶谐波扰动振幅3个参数。

通过对现阶段有关非牛顿流体射流失稳破碎过程的理论分析。可以发现，描述流体幂律/黏弹特性的参数如稠度系数、变形延迟时间、未松弛拉应力等参数的大小和外部物理场如静/交变电场、环境的传热传质效应等均会直接影响黏弹性流体射流的失稳与破碎进程。将相关问题由线性稳定性分析推广至弱非线性稳定性分析，可以进一步发现表面波扰动的二阶谐波是导致液膜或射流发生破碎断裂并最终液丝的主要原因。

1.2 非牛顿流体射流初次雾化实验

相较于传统的牛顿流体，非牛顿流体因其具有的高黏度和非线性的流变特性，导致其雾化过程相较于牛顿流体来说更为困难。液体射流在离开喷嘴出口附近，液体射流表面波的发展过程、射流破碎长度和破碎时间等与牛顿流体射流会有较大地不同。因此，需要通过实验研究得到非牛顿流体射流初次雾化过程中的相关特性参数。在火箭发动机工作过程中，不同喷嘴的结构与设计对射流初次雾化的性能起到了重要的作用。具体而言，不同的喷注方式会影响液体射流初次雾化过程中射流的产生和失稳过程。对于非牛顿流体射流，在实际应用中通常使用离心式喷嘴、撞击式喷嘴和气助雾化式喷嘴对非牛顿射流进行雾化。首先对上述几种不同喷嘴的特性和主要设计参数进行简要地介绍。

对于离心式喷嘴，根据现有的实验结果可以发现，利用其很难将非牛顿流体射流进行高质量的雾化。具体而言，在某一确定的压降下利用离心式喷嘴进行雾化，可以使得水射流形成完全发展的喷雾锥。然而，对于非牛顿流体射流，由于其自身性质，只能够形成螺旋不稳定形的圆柱形射流。此外，利用离心式喷嘴较难使得液体射流完全破碎成为一系列尺寸不同的小液滴，而形成一系列破碎长度较大的液丝。在设计中，切向孔通道长度、个数，旋流室直径等参数都会影响离心式喷嘴的雾化质量。

对于撞击式喷嘴，其主要是利用高速液体射流的动能来使其发生破碎，实验结果说明撞击式喷嘴对非牛顿流体射流的雾化效果较好。此外，相较于其他种类的喷嘴撞击式的结构较为简单，同时也不需要额外的装置来诱导射流的破碎。因此，撞击式喷嘴在非牛顿流体射流的雾化中得到了广泛地应用。在设计中，喷嘴出口个数、射流撞击角度等决定了撞击式喷嘴的雾化质量。

对于气助式喷嘴，其主要是利用具有高动量的气体与液体射流混合进行雾化。实验同时表明，气助式喷嘴对非牛顿流体射流可以达到较好地雾化效果。气助式喷嘴在非牛顿流体射流的雾化中同样应用较为广泛。在设计中，气液面积比是影响气助式喷嘴雾化质量的重要参数。

还有研究者利用超声雾化喷嘴以及气泡雾化喷嘴对非牛顿流体射流的雾化进行了研究。利用这2种喷嘴可以在相对较低的压降下产生数量较多的小液滴。此外，还可以利用外加振荡型的喷嘴，人为地引入能量输入来促进非牛顿流体射流发生破碎与雾化。

因此，接下来将对相关非牛顿流体射流通过不同种类喷嘴发生初次雾化时的实验研究进展进行总结。

1.2.1 离心喷嘴初次雾化实验

液体射流通过离心喷嘴后，会根据液体性质和工况的不同而产生不同的破裂模态。利用黏弹性流体通过离心喷嘴发生初次雾化后，所产生不同的破碎模态如图11所示[20]。

图11 非牛顿流体射流在通过离心喷嘴后所产生不同的破碎模态[20]

根据Thompson和Rothstein[20]研究得到的结果，可以发现，随着液体供应压力的不断提高，射流会经历扭曲射流，螺旋射流以及完全发展等不同的破碎模态。在液体射流的表面，可以清楚地观察到表面波的产生及发展过程，由于非牛顿流体自身的性质，会在射流表面形成手指状的凸起；随着表面波振幅的变大，液体射流会发生破碎，并形成大量的液丝结构。

根据上述所得到的实验结果，可以进一步地对不同来流条件下所对应的破碎模式进行归纳总结，得到利用离心喷嘴对非牛顿流体射流进行初次雾化过程的破碎模态相图，如图12所示[20]。

根据图12可以发现，在不同的韦伯数以及弹性数下，射流的初次雾化过程表现出不同的破碎模态。具体而言，随着来流韦伯数的不断增大，射流以此表现出瑞利破碎、射流分叉、稳定封闭锥、部分锥以及破裂锥模式。

图12 非牛顿流体射流通过离心喷嘴后的破碎相图[20]

此外，Yang等[21]利用水和以凝胶模拟液为代表的幂律流体通过旋流室内安装簧片结构的离心喷嘴进行雾化实验。同时，对所得到的实验结果进行了比较，利用高速相机拍摄记录了液膜破碎的详细过程，并通过改变喷嘴的结构参数来研究喷嘴几何参数和簧片对射流初次雾化特性的影响。实验结果表明，在初次雾化的过程中，凝胶模拟液的喷雾结构与水的射流结构具有很大的不同。具体而言，凝胶模拟液的射流发展结构会随着压降的变化产生不同，主要可分为以下几种形式，分别为：柱状射流、扭曲旋流液膜、液网结构和完全发展的空心锥结构。此外，进一步分析了旋流室内簧片对射流形态的影响。实验结果表明，簧片的加入会增加喷嘴的流量系数并减小喷雾锥角，这将使得液体射流在一定距离内的伸展效应下降。在一定压降下，液体射流的破碎长度也会随着簧片结构的安装而增大。

同时发现，离心喷嘴的结构参数对射流雾化质量具有很大影响。Yang等[22]研究了几何特性参数对离心喷嘴所产生幂律流体射流初次雾化特性的影响。研究结果表明，初次雾化时凝胶推进剂通过离心喷嘴所产生完全发展模式的液膜可以进一步地分为4个区域，分别为：完整的锥形液膜区域、液膜和液丝共存区域、液网区域和液丝液滴共存区域，相关的实验结果如图13所示[22]。此外，随着几何特性参数的不断增大，锥形液膜在初次雾化过程中的破碎长度和喷雾锥角会增大，而流量系数会逐渐减小。

图13 由离心喷嘴所产生的完全发展模式的凝胶液膜[22]

除几何结构参数外，离心喷嘴中不同的流体进口通道形状也会对液体射流的初次雾化特性产生影响。Fu和Cui[23]研究了存在非切向进口通道离心喷嘴的幂律射流初次雾化特性。可以发现，2种喷雾场最显著的区别为：非切向进口通道喷嘴射流锥的形状会发生脉动。这一脉动的产生原因主要是由于旋流腔内所剩余可压缩空气体积的变化而导致的。同时，通过非切向进口通道进入旋流腔流体的漩涡半径会同时降低，这将导致所产生喷雾锥角的减小。

近年来，Fu等[24]研究了以凝胶推进剂为代表的幂律流体通过敞口式离心喷嘴时的初次雾化特性。敞口式离心喷嘴可以与其他类型的喷嘴组合成为同轴喷嘴。在实验中利用了3种不同流变性质的凝胶模拟液以及3种不同几何特性参数(不同切向进口通道数量、位置、长度等)进行了喷雾实验，并利用电导法测量了喷雾场中液膜的厚度。实验图像如图14所示[24]。

图14 不同压降和几何特性参数下凝胶推进剂的雾化图像[24]

通过实验测量得到了在初次雾化过程中的液膜厚度、流量系数、喷雾锥角和破碎长度随几何特性参数以及流变特性的变化规律，拟合得到了有关的经验公式。为未来敞口式离心喷嘴的设计提供了实验数据的支持。

1.2.2 撞击式喷嘴初次雾化实验研究

通过以上实验可以发现，由于凝胶推进剂自身的流变性质，利用离心喷嘴有时难以取得好的雾化效果。因此，对于非牛顿流体射流，也经常采用撞击式喷嘴对其进行雾化。不同来流条件下撞击式喷嘴的破碎模态如图15所示[25]。

通过图15以及相关的研究[26-27]可以发现，根据非牛顿流体种类以及撞击速度的不同，液膜的表面会产生多种形式的表面波，表面波的不断发展将导致液膜失稳并发生破碎。表面波的不断发展，同时会在液膜的边缘形成鱼骨结构等不同的收缩形态，最终导致大量的液丝和液滴从液体射流的表面脱落。

图15 非牛顿流体射流在通过撞击喷嘴后所产生不同的破碎模态

根据实验结果，对不同来流条件下不同种类幂律凝胶射流的破碎模式进行总结归纳，得到利用撞击式喷嘴对非牛顿流体射流进行初次雾化过程的破碎模态相图，如图16所示[28]。对于幂律凝胶，其广义雷诺数可以定义为

图16 非牛顿流体射流通过撞击式喷嘴后的破碎相图[28]

(1)

式中：n为流变系数；κ为与稠度系数有关的表达式；ρl、ul分别为液体的密度和速度。

可以发现，撞击式喷嘴所产生液膜的破碎模式与等效雷诺数以及韦伯数有关。具体而言，随着幂律凝胶种类的不同，随着等效雷诺数以及韦伯数的提高，会依次产生液丝液滴破碎、液丝断裂和完全发展破碎模式。不同幂律凝胶之间破碎模式转捩雷诺数的大小同样是不相同的。

Yang等[29]采用撞击式喷嘴对幂律凝胶推进剂进行实验研究。为理解平面射流表面波的发展过程以及其失稳机理，首先研究了撞击式喷嘴所产生平面射流的稳定性问题，再通过求解色散方程得到扰动波数和增长率之间的色散关系。随后，通过高速相机对液膜破碎的图像进行拍摄，进一步处理所得到的图像，得到实际液膜破碎长度等初次雾化参数随流动参数的变化规律。在实验中，同时观察到表面波的产生及发展过程，理论与实验的对比结果表明：线性稳定性理论可以较好地预测幂律流体在撞击式喷嘴中破碎长度和其所产生表面扰动波波长的大小。

与离心式喷嘴相似，撞击式喷嘴出口的形状会对液膜的初次雾化过程产生影响。Fu等[30]通过一系列的实验研究了撞击式喷嘴出口几何形状对以凝胶推进剂为代表的幂律流体初次雾化特性的影响，实验结果如图17所示[30]。实验表明，在一定压降下，由矩形或椭圆形喷嘴出口撞击后所形成的液膜要比圆形喷嘴出口所形成的液膜表面波的发展过程更加迅速。

图17 长宽比对矩形出口撞击式喷嘴雾化性能的影响[30]

此外，Zhao等[31-32]研究了两束低速幂律射流发生碰撞后，产生平面射流中表面波的发展过程。通过理论计算的方法得到了平面射流长度及厚度随液体速度的变化规律，并利用实验对理论预测进行了验证，可以发现理论计算结果与实验符合较好。进一步研究了稠度系数以及幂律指数对平面液膜形状的影响。结果表明，稠度系数以及幂律指数对平面射流的铺展产生了双重效应。

通过对现有关于凝胶推进剂在不同种类喷嘴条件下发生初次雾化的实验研究。可以发现，不同的流动及流变参数会影响非牛顿流体射流的初次雾化过程。同时，上述参数对喷雾锥角和破碎长度等初次雾化特性参数产生了显著的影响。在未来的研究中，可以考虑在多物理场(如电场、高温、背压环境等)条件下研究不同种类非牛顿流体的初次雾化特性。

1.2.3 气助式喷嘴初次雾化实验研究

与牛顿流体相比，非牛顿流体因其自身高黏度与非线性的流变特性，导致其利用普通喷嘴进行雾化时的效果并不理想。近年来，有研究者使用气助式喷嘴对非牛顿流体射流进行雾化。由于气助式喷嘴结构简单、易于加工等特点，在实际使用过程中也经常使用气助式喷嘴对凝胶推进剂进行雾化。其主要利用高速气流与液体射流之间的气液剪切作用，将高速气体的动量传递给液体射流，最终使得液体射流发生破裂。

在不同来流条件下，Ciezki等[33]利用气助式喷嘴对幂律型流体射流进行雾化，所得到的破碎模态如图18所示[33]。

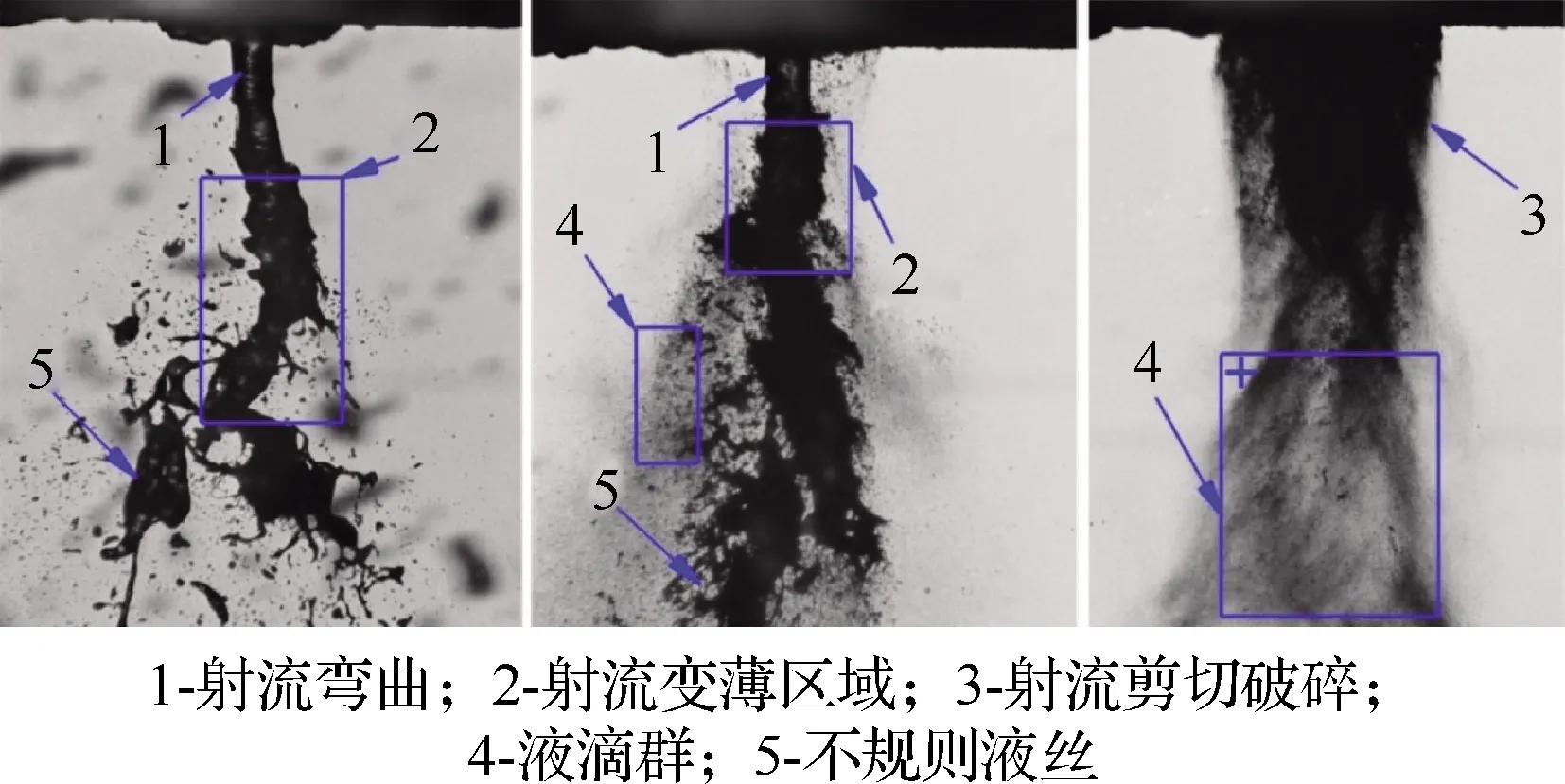
图18 非牛顿流体射流在通过气液同轴喷嘴后所产生不同的破碎模态[33]

根据所得到的实验结果可以发现，在气助式喷嘴中，气液动量比是判别射流破碎模态的依据之一。不同量级的气液剪切作用会在液体射流表面产生不同形式的表面波，表面波振幅的不断放大最终导致了液体射流的失稳。随着气液动量比的不断提高，空气动力的增强将促进液体射流的破碎进程。在初次雾化过程结束后，会在喷雾场内形成大量的液丝结构(进一步提高气液动量比会使得液丝进一步破碎形成液滴)。

进一步地，Zhao等[34]将利用气助式喷嘴对非牛顿流体射流进行初次雾化过程中产生不同的破碎模态相图总结归纳如图19所示。其中，非牛顿流体的奥内佐格数和韦伯数分别定义为

(2)

(3)

式中：τ0为屈服应力；D0为射流直径；K为稠度系数；n为幂律指数；φ为经验常数，取φ=3.2×10-4。

根据图19可以发现，在不同韦伯数以及奥内佐格数下，射流的初次雾化过程表现出不同的破碎模态。具体而言，当射流的奥内佐格数较大且韦伯数较小时，射流表现出瑞利破碎模式；提高来流韦伯数，射流表现出纤维破碎模式；进一步提高来流韦伯数并降低奥内佐格数，射流的破碎模式将转换为雾化模式。

图19 非牛顿流体射流通过气助式喷嘴后的破碎相图[34]

此外，Geckler和Sojka[35]利用气泡雾化喷嘴对黏弹性流体射流进行了实验研究，实验所得到的初次雾化过程图像如图20所示。

图20 利用气泡雾化喷嘴进行实验时所得的雾化图像[35]

实验结果表明，由于在液体射流内部引入了大量的气泡，气泡的变形及破碎会促进液体射流的失稳。实验表明，利用气泡雾化喷嘴可显著地减小液体射流的破碎长度。此外发现，所使用的非牛顿流体中，聚合物的浓度以及高分子物质的分子量都会对液体射流的破碎长度产生影响。

Mansour和Chigier[36]利用气助式直流喷嘴对黏弹性流体射流进行初次雾化过程进行了实验研究。结果表明，黏弹性流体射流的初次雾化过程与气液动量比、气体韦伯数及雷诺数有关。提高气液动量比可以显著地加快非牛顿流体射流的初次雾化进程。此外，Hermosin-Reyes等[37]利用气液内混式喷嘴对黏弹性流体射流的初次雾化过程进行了实验研究。结果表明，由于黏弹性流体自身的拉伸特性，液体射流在离开喷嘴出口附近会产生明显的拉丝现象。这一效应会随着聚合物浓度的增加而更加显著。实验结果同样证明了射流的破碎长度会随着气液动量比的增大而减小。

通过研究发现，有关使用气助式喷嘴对非牛顿流体射流初次雾化的实验研究仍较为有限。因此，在未来的研究中，可以对不同种类非牛顿流体射流通过气助式喷嘴进行实验研究，以获得更加具有普适性的结果。

1.3 流变参数对射流初次雾化的影响

相较于牛顿流体射流，非牛顿流体射流因其自身非线性的流变特性，射流的破碎长度等会受到非牛顿流体流变参数的影响。接下来，将对不同流变参数对非牛顿流体射流初次雾化特性的影响进行总结分析。

在剪切流动中，现存多种不同的描述切应力与速度梯度之间关系的本构方程。根据本构方程的不同，可以将非牛顿流体进一步地分为塑性流体、假塑性流体、屈服-假塑性流体等。

对于塑性流体，在描述其流变特性的本构方程中，屈服应力τ0表征了流体从只发生变形向发生流动过程转换时，剪切力的相对大小。Csizmadia等[38]在实验中研究了在塑性流体中，屈服应力的大小对液体射流破碎长度的影响。所得的实验结果如图21所示。

图21 不同屈服应力下塑性流体射流长度的变化规律[38]

实验结果表明，塑性流体在初次雾化过程时的破碎长度与其自身的屈服应力有关。屈服应力的提高会导致右图射流的破碎长度增加。

对于假塑性流体，其本构方程中稠度系数K以及流变系数n表征了流体在流动时剪切黏度的相对大小。在假塑性流体中，切应力与速度梯度满足幂指数关系，因此，假塑性流体也被称为幂律流体。当流变系数n=1时，假塑性流体将退化为牛顿流体。对于假塑性流体射流的初次雾化过程，Fu等[24]对不同稠度系数及流变系数的假塑性流体通过离心式喷嘴所产生液膜的初次雾化过程进行了实验研究，结果如图22所示。

图22 不同流变参属下假塑性流体的初次雾化过程[24]

可以发现，在实验中稠度系数和流变系数会随着流体种类的不同而同时发生变化。具体而言，液体射流的破碎长度会随着稠度系数的增大而增加；同时，可以更加清楚地观察到射流初次雾化过程结束后所产生的液丝结构。

对于屈服-假塑性流体，该种流体同时具有塑性流体以及假塑性流体的特点。具体而言，其具有一定的屈服应力τ0，当剪切应力小于屈服应力时，流体将保持固体的形态而不发生流动；当剪切应力大于其屈服应力时，流体将会发生流动，且切应力与速度梯度之间满足幂律关系。相关物理量也可用稠度系数以及流变系数来进行表征。

Zhao等[34]研究了多种具有不同屈服应力、稠度系数以及流变系数的屈服-假塑性流体射流在通过气液同轴喷嘴后的初次雾化过程，相关实验结果如图23所示。

根据图23所得到的实验结果，可以发现，在气液速度几乎相同的前提下，具有不同流变参数的屈服-假塑性流体在初次雾化过程中会表现出不同的射流破碎形态。可以观察到射流表面不稳定波的发展过程，同时可观察到射流表面的褶皱和凸起结构；在射流即将发生破碎时，会观察到拉丝等物理现象。

图23 不同种类水煤浆流体通过气液同轴喷嘴发生初次雾化的实验图像[34]

此外，Jejurkar等[39]研究了金属颗粒的加入对屈服-假塑性液体射流初次雾化特性的影响。可以发现，随着金属颗粒的加入，液体射流在初次雾化过程中会产生新的破碎模态。此外，金属颗粒的加入同时会改变流体的表面张力、黏度和密度等物性参数，最终将导致射流破碎长度的增大。

对于黏弹性流体，由于该种非牛顿流体在流动的过程中同时具有黏性与弹性。因此需同时考虑其剪切流变以及拉伸流变特性。对于其剪切流变特性，在航天推进领域内常使用Oldroyd-B本构关系式描述其切应力与速度梯度之间的关系。具体而言，通常使用应力松弛时间λ1、变形延迟时间λ2和两者之间的时间比λ来描述其流变特性参数。Negri和Ciezki[40]通过实验研究了时间比对黏弹性流体初次雾化时射流破碎长度的影响，相关的实验结果如图24所示。

图24 时间比对黏弹性液膜破碎长度的影响[40]

可以发现，在射流速度等其他流动参数相等的前提下，随着时间比的增大，黏弹性流体射流的破碎长度会显著地增大。所得到的实验结论同时证明了理论分析的正确性。

此外，通过实验研究进一步发现，时间比这一流变参数的取值会受到流体自身物理性质的影响。具体而言，时间比会随着流体内部所含高分子聚合物分子量及浓度的增高而增大。因此，根据Negri和Ciezki[40]的实验也可以发现，射流的破碎长度也会随着聚合物分子量及浓度的提高而增大。

对于黏弹性流体的拉伸流变特性，常利用拉伸黏度这一参数进行描述。拉伸黏度定义为流体在垂直于流动方向上横截面所承受拉应力于拉伸应变速率的比值。Dinic和Sharma[41]研究发现，拉伸黏度会随着黏弹性流体内部高分子聚合物浓度及分子量的提高而增大。Mun等[42]研究了液体射流破碎长度随黏弹性流体拉伸黏度的变化规律。实验结果表明，黏弹性流体的破碎长度会随着流体拉伸黏度的提高而显著增大。

此外，对于黏弹性流体，在拉伸流动的过程中，会使用弹性储存模量G′来表征其发生形变时，由于弹性形变而储存的能量。弹性储存模量越大，说明流体的弹性效应越大。McCabe和Coil[43]研究了在不同弹性储能模量下，黏弹性流体在通过撞击式喷嘴进行初次雾化时所产生的不同破碎模态，所得结果如图25所示。

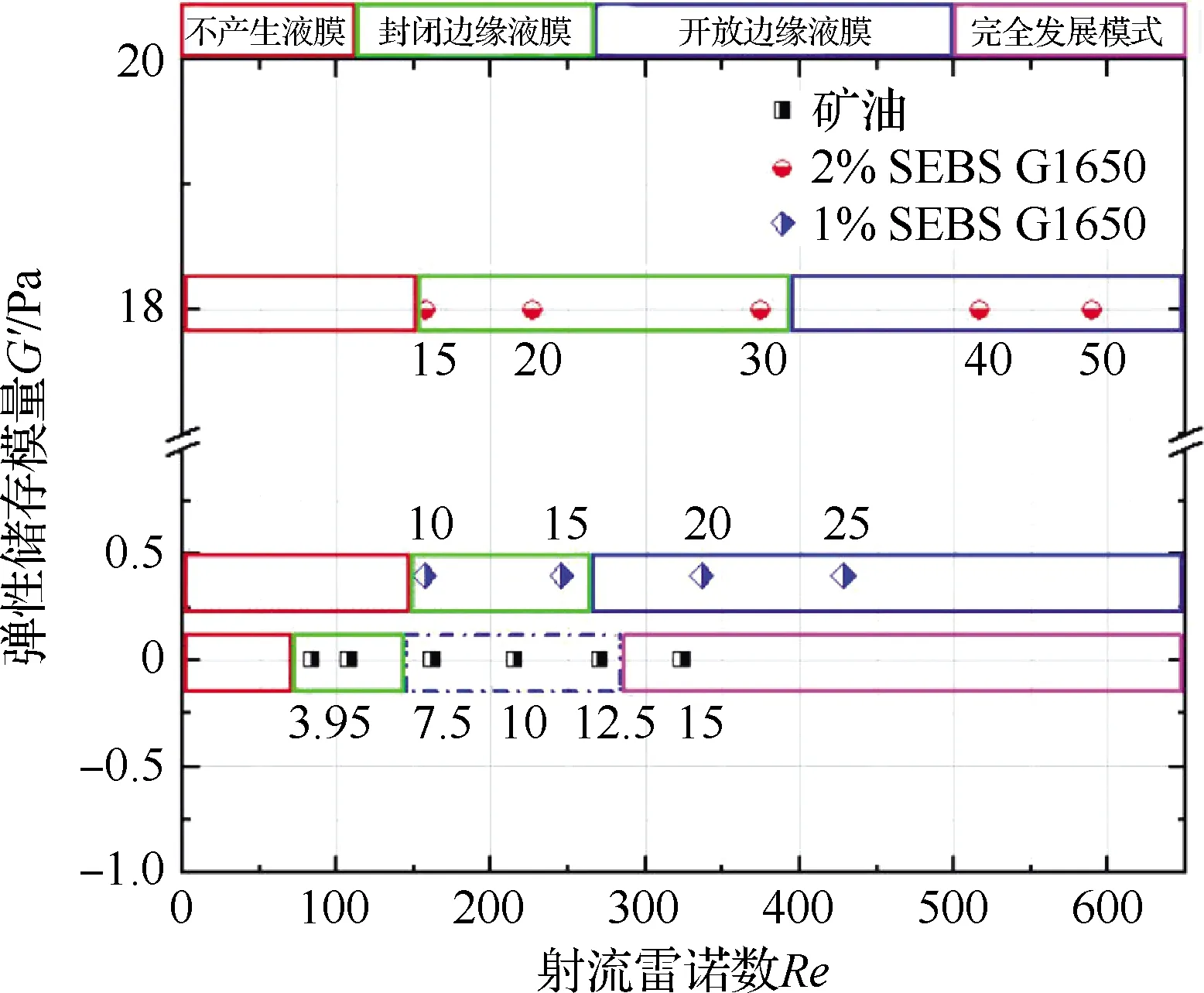
图25 不同弹性储存模量的黏弹性流体在通过撞击式喷嘴雾化时所产生的不同破碎模态[43]

可以发现，随着弹性储存模量的增大，流体的弹性效应将增强。这说明了在相同的雷诺数下，液体射流会更加难以雾化。当流体的弹性储存模量较小时，射流在雾化过程中会产生完全发展这一破碎模式。然而，当弹性储存模量增大后，这一破碎模式将会消失。这说明了剪切流变参数相同的黏弹性流体，可能会因为拉伸流变参数的变化，而导致不同的破碎特性。

总之，对于非牛顿流体射流初次雾化过程中表面波的发展过程进行理论分析以及实验观测可以发现，利用稳定性分析的手段可以较为准确地预测表面波的增长率以及射流的破碎长度等初次雾化参数；通过数学推导得到表面波增长率随不同流变、流动参数的变化规律；进一步地，利用实验测量的手段可以对理论分析得到的结论进行验证，以证明稳定性理论的正确性。

2 非牛顿流体液滴二次雾化特性

当射流表面的扰动波振幅与射流厚度在同一数量级时，射流会发生失稳和破碎，并在完成初次雾化进程后，形成大量尺寸不同的液滴。液滴在高速气流的作用下会进一步地发生拉伸、变形和破碎等物理现象。液滴的二次雾化过程是液体射流在整个雾化过程中重要的组成部分。在本文的这一部分，对于非牛顿流体液滴，现阶段相关的理论研究开展较少，研究者多采用与研究牛顿流体液滴二次雾化类似的实验观测法对非牛顿液滴二次雾化拉伸、变形及破碎细节进行研究。在非牛顿流体液滴的二次雾化研究方面，Theofanous等[44]对某些种类液滴的二次雾化过程进行了总结归纳。接下来，将对非牛顿流体液滴的破碎模态、不同种类非牛顿流体液滴二次雾化的变形及破碎特性进行综述。

2.1 液滴的破碎模态

液滴的二次雾化过程是由于液体的表面张力、空气动力和黏性力之间的相互作用而发生的。因此，在不同的来流条件下，液滴会展现出不同的破碎模态。有研究者[45]对其进行了较为详细的研究。研究结果发现，不同的来流速度会导致液滴产生不同的破碎模态。在亚声速气体来流的条件下，按照最普遍的划分方式，液滴的破碎模态分别为：振荡破碎模态、袋式破碎模态、袋蕊破碎模态、多模态破碎模态、剪切破碎模态和灾难破碎模态。有关非牛顿流体液滴在横向气流下不同破碎模态的简图如图26所示[46]。

接下来，对上述几种不同破碎模态的主要特征进行简要阐述。对于振荡破碎模态，事实上并不是在所有实验中都能够观测到该模态的发生。当液滴在气流中的振荡频率接近于自身的固有频率时，液滴可能发生破裂并产生几个较小的液滴。此时，小液滴的尺寸和初始液滴的大小在同一个数量级上。

随着气流速度的提高，液滴的破碎模态将转变为袋式破碎模态。在袋式破碎模态中，液滴会因气动力的作用而变为椭球形，同时在液滴中心较薄的区域会形成一个液袋。此时，液滴的结构主要包括因气动力而产生的厚度较薄的液袋(Bag)以及厚度较厚的液环(Rim)。在气流的作用下，液袋首先发生破裂，随后液环会发生进一步的破碎。袋式破碎模态的有关实验现象及变形破碎规律在Zhao等[47]和Kulkarni和Sojka[48]的研究中进行了详细地分析与讨论。

袋蕊破碎模态会在气流速度进一步提高时发生。其主要变形破碎特征与袋式破碎模态是相似的。然而，在液袋生长的过程中，多模态破碎会在其中央产生一个类似于“花蕊”的结构，“花蕊”结构的生长方向与液袋的发展方向相反。在气流的作用下，液袋首先发生破裂，随后液环和“花蕊”结构在气动力的作用下，发生进一步的破碎，产生不同尺寸的小液滴群。Zhao等[49]和Dai和Faeth[50]通过实验观测，对多模态破碎的实验图像以及所产生花蕊结构的变形破碎规律进行了分析。当气体来流的速度进一步提高时，袋蕊破碎模态就会转换成为多模态破碎模态。与袋蕊破碎模态相比，多模态破碎模态会产生多个袋装结构，袋结构的个数与位置和气体来流的速度有关[46]。

进一步提高来流气体的速度，液滴的破碎模态会转变成为剪切破碎模态。在剪切破碎模态中，更小的液滴会因气动剪切作用而不断地从液滴边缘上脱落。脱落后的小液滴会在高速气流中发生进一步地破碎，最终产生大量小尺度的液滴。

当来流气体速度很高时，液滴的破碎模态会转变成为灾难破碎模态。在该模态下，液滴变形最显著的特征是在其迎风表面产生了瑞利-泰勒(Rayleigh-Taylor)不稳定波，这些扰动波会随时间而不断发展，最终导致液滴发生破碎，并在流场下游产生了大量的小液滴。因此，灾难破碎模态也被称为扰动波剥落模态。有关剪切破碎模态和灾难破碎模态的实验结果将在下面的小节内进行分析。

2.2 不同种类非牛顿流体液滴的二次雾化现象

2.2.1 伯格流体液滴的二次雾化现象

伯格流体(Boger Fluid)是一种黏性大小不随剪切作用变化且具有弹性的非牛顿流体。这种流体在流动时表现出黏性液体的性质，然而在拉伸时却表现出弹性固体的性质。可以通过向高黏度牛顿流体中加入一定量的高分子聚合物来制备伯格流体。Wilcox等[51]通过实验观测的方法，最早研究了伯格流体液滴的二次雾化特性。他们利用激波管法测试了不同浓度聚合物溶液产生的液滴在超声速气流下所发生的二次雾化过程，实验结果如图27所示[51]。

图27 伯格流体液滴的二次雾化过程[51]

研究结果表明：即使加入高分子聚合物的含量很低，液滴的二次雾化过程也会被延缓。同时证实，伯格流体液滴二次雾化的过程和牛顿流体液滴是相似的，但是在液滴表面会有更多的液丝而非小液滴剥落下来。在二次雾化过程结束后，所产生液丝的尺寸大约为牛顿液滴破碎后小液滴大小的1.5倍量级。Matta和Tytus[52]利用高速风洞研究了伯格流体液滴发生二次破碎后质量平均直径(MMD)的大小。结果发现，伯格流体液滴二次雾化过程结束后，所产生的小液滴直径比牛顿液滴大一个数量级。这说明伯格流体液滴在相同的流动条件下比牛顿流体液滴更加难以破碎和雾化。

Arcoumanis等[53-54]利用高速摄影技术对不同直径的液滴在高速气流场中的二次雾化过程进行了拍摄。对于伯格流体液滴，实验只观测到液滴的剪切破碎模态，有关结果如图28所示[53]。

图28 伯格流体液滴在高速气流中的破碎[53]

可以发现，高速气流所导致的空气动力在液滴表面产生不稳定波后，进一步发展会发生破碎并产生液丝。随着聚合物浓度的增加，液滴的破碎时间也会相应地增大。Shraiber[55]所进行的实验也获得了相似的结果。Lee和Reitz等56]和Liu和Reitz[57]在研究碳氢燃料液滴的二次雾化过程时也发现液滴的二次雾化过程要比牛顿流体液滴更加复杂和缓慢。

Dinh等[58]对脉冲爆震发动机中所使用的液体碳氢燃料液滴在高马赫数与低韦伯数下的二次雾化过程进行了实验研究，高速摄影的结果如图29所示。实验发现，当液滴中聚合物的浓度较高时，液滴在高速气流中发生二次雾化后同样不会破碎为小液滴，而是形成了一系列尺寸不同的液丝结构。

图29 低韦伯数条件下，聚合物浓度对液滴二次雾化特性的影响[58]

2.2.2 幂律流体液滴的二次雾化现象

美国普渡大学Sojka课题组对幂律流体液滴的二次雾化过程进行了大量的研究。Snyder等[59-62]对黄原胶溶液液滴的二次雾化过程进行了实验研究与理论分析，黄原胶溶液液滴的袋式破碎模态如图30所示[61]。

图30 黄原胶溶液液滴的袋式破碎模态[61]

实验结果发现，在大多数破碎模态下，黄原胶溶液液滴的破碎形态与牛顿流体液滴大致相同，只是在袋式破碎模态中液袋的结构与尺寸存在着一些差异。袋式破碎模态完成后，所得到的液丝尺寸不满足经典的高斯分布。此外，还就黄原胶溶液液滴二次雾化的时间特性和破碎后液丝的尺寸分布进行了实验研究。利用PIV等技术对液滴二次破碎后产生的液丝的速度分布等进行了详尽地测量，并将测量结果与水滴破碎后的结果进行对比。结果表明，黄原胶溶液液滴破碎后会产生更大的液丝，同时大尺寸液丝所占的比例相对较高，不同液丝之间速度分布的方差也相对较大。可以发现，应用于传统牛顿流体液滴中表征液滴变形及破碎特性的无量纲参数(如韦伯数We、奥内佐格数Oh等)无法对黄原胶溶液液滴的变形及破碎特性参数进行预测和表征。此外，通过实验研究了幂律流体液滴二次雾化时袋式破碎和多模态破碎下液滴的变形特性。与先前其他研究者得到的理论数据进行对比，产生了很大的误差。

Lopez等在文献[63-64]中研究了甘油添加羧甲基纤维素溶液液滴的二次雾化特性。与Snyder等[61]的研究结果相似，他们发现液滴二次雾化所产生的破碎模态与牛顿液滴相比差异不大，但同样在液滴破碎后会产生较多的液丝而非小液滴。Rocha[65]在他的学位论文中研究了同种溶液液滴在袋式和多模态破碎模态下液滴变形和破碎参数随来流气体速度的变化规律。实验拍摄的结果如图31所示。

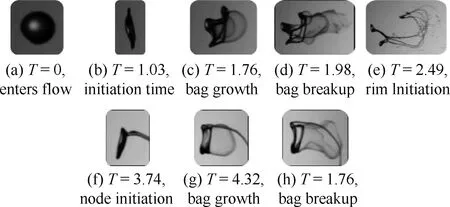
图31 非弹性非牛顿流体液滴袋式破碎图像[65]

国内也有研究者对此问题展开了一系列实验研究。南京理工大学的邓寒玉等[66-68]为研究幂律凝胶液滴二次雾化的特性。通过实验可以发现，当幂律凝胶液滴的流动指数大于一临界值时，临界韦伯数Wec会随幂律指数的增加而显著增大。实验结果表明：当韦伯数小于一临界值时，煤油液滴的表面剥离速度会大于煤油凝胶；当韦伯数大于该临界值时，两者的剥离速度相差不大。

孔上峰等[69-71]以煤油凝胶和煤油为工质，利用高速摄影技术研究液滴的二次雾化过程，得到了不同液滴破碎模态下的临界韦伯数。同时研究了奥内佐格数Oh对总破碎时间的影响，实验结果如图32所示[70]。

实验结果表明，煤油凝胶液滴的二次雾化过程总体上与牛顿流体液滴相似。然而，在多模态破碎模态下，煤油凝胶液滴在发生变形时，液滴表面会产生褶皱。与煤油液滴二次雾化的过程相比，煤油凝胶液滴在变形的过程中，所形成袋结构的横向长度比煤油液滴要小。此外，袋结构边缘的液环结构与煤油液滴相比较不规则。

2.2.3 宾汉流体液滴的二次雾化现象

宾汉流体(Bingham Fluid)是一种具有屈服应力，同时切应力与切应变之间满足线性关系的流体。水煤浆(CWS)作为一种典型的宾汉流体，广泛地应用在管道内煤粉的输运过程中。下面对以水煤浆为代表的宾汉流体的二次雾化过程所进行的实验研究进行总结。

Zhao等[72-73]研究了水煤浆液滴的二次破碎过程，作为一种典型的宾汉流体，其变形与破碎特性和牛顿流体液滴存在着较大的差别，实验结果如图33所示[72]。

图33 水煤浆的袋式破碎模态[72]

实验结果表明，水煤浆液滴的二次雾化过程只存在3种破碎模态，分别为：振荡破碎模态、多模态破碎模态和剪切破碎模态。对实验数据进行进一步地分析发现，在牛顿流体液滴二次雾化中所使用的表征液滴变形破碎特性的无量纲特征数已无法满足区分水煤浆不同破碎模态的需求。因此，引入了表征流体屈服应力的无量纲参数X和He数，重新对水煤浆液滴二次雾化过程的破碎相图进行了划分。结果发现所提出的划分依据与实验数据符合较好。

此外，以水煤浆液滴二次雾化过程为实验对象。研究了在袋式破碎模态下，液滴表面不稳定波的波长和液滴子袋个数之间的关系，创造性地提出利用R-T不稳定波的波数对水煤浆液滴二次雾化的破碎模态进行划分。再利用半理论的分析方法，对水煤浆液滴二次雾化破碎模态的相图进行了预测，并通过实验证实了该理论的有效性。

2.2.4 Herschel-Bulkley流体液滴的二次雾化现象

赫歇尔-布勒克利流体(Herschel-Bulkley Fluid)是一种具有屈服应力且切应力与切应变之间满足幂指数关系的流体。作为一种水溶液增稠剂，卡波姆(Carpol)溶液常常被用于工业领域中。有关卡波姆溶液的喷雾特性已经有学者进行了研究[74]。然而，对于单个卡波姆凝胶液滴的二次雾化过程至今仍较少地被研究过。下面对以卡波姆凝胶液滴为代表的Herschel-Bulkley流体液滴的二次雾化过程中所做的实验研究进行总结。

宋少波[75]以卡波姆溶液为工质，通过实验观测的方法，研究了卡波姆凝胶液滴的二次雾化特性，实验结果如图34所示。

图34 卡波姆凝胶液滴剪切破碎模态的实验图像[75]

通过实验的观测可以发现，卡波姆凝胶液滴的二次雾化过程与水滴有很大的区别。在剪切破碎模态下，卡波姆凝胶液滴破碎后基本上不产生小液滴，而是产生大量细长形的液丝。这一效应随着卡波姆溶液浓度的升高而增强。

此外，增加来流气体的速度，对于卡波姆凝胶液滴的二次雾化过程，通过实验观察到了一种被称为“双袋-多袋”的破碎模态。有关的实验现象如图35所示[75]。

图35 卡波姆凝胶液滴双袋-多袋破碎模态的实验图像[75]

可以发现，所产生的“双袋-多袋”破碎模态，主要由2部分组成。在卡波姆溶液浓度较低时，该模态由袋蕊破碎模态发展而来；在卡波姆溶液的浓度较高时，会观察到类似于剪切破碎的多袋破碎。

2.3 非牛顿流体液滴变形及破碎特性

与牛顿流体液滴相似，不同种类的非牛顿流体液滴在高速气流中也会发生变形并最终破碎。利用实验观测的方法，对非牛顿流体二次雾化过程中所涉及的变形及破碎特性进行了研究。

1)二氧化硅质量分数为1%时

(4)

2)二氧化硅质量分数为2%时

(5)

3)二氧化硅质量分数为3%时

(6)

可以发现，煤油凝胶液滴的最大变形率随韦伯数的增大表现出先增大后减小的趋势。具体而言，当气体来流韦伯数较小时，液滴在流场中所受到的剪切力不大，可以近似为高黏度的牛顿流体，因此，最大变形率随韦伯数的增加而增大。当来流韦伯数较大时，液滴在开始变形阶段受到的剪切力很大，其自身黏度会迅速降低，表现出类似于低黏度牛顿流体二次雾化的特性。随着气流和液滴相对速度的降低，液滴所受到的剪切速率不断减小，导致其黏度增加，变形速度减缓，最终会导致最大变形率的减小。

此外，还研究了煤油凝胶液滴的总破碎时间Ttot随奥内佐格数Oh的变化规律，所得到的经验公式为

1)二氧化硅质量分数为1%时

Ttot=5.43Oh+0.8

(7)

2)二氧化硅质量分数为2%时

Ttot=40.45Oh-0.228

(8)

3)二氧化硅质量分数为3%时

Ttot=-9.94Oh+3.66

(9)

实验结果表明，与煤油液滴的二次雾化的时间特性相比，煤油凝胶液滴的总破碎时间并不是随奥内佐格数的增加而单调变化的。通过计算发现，所有煤油凝胶液滴的总破碎时间大致均在1.5～3之间，该值与煤油液滴破碎时相似。

曹钦柳等[76]研究了煤油凝胶液滴的时空破碎特性，研究了总破碎时间与初始变形时间Tini的比值随奥内佐格数的变化规律，并得到以下的拟合曲线：

1)0.024

(10)

2)0.015

(11)

3)0.23

(12)

可以发现，不同质量分数下煤油凝胶液滴总破碎时间与初始变形时间的比值均随着奥内佐格数的增大而减小。同时，该规律也说明了当煤油凝胶液滴发生破碎时，其流变特性会在变形的过程中更趋于煤油液滴。

Zhao等[72]对以水煤浆液滴为代表的宾汉流体二次雾化过程中的变形及破碎特性进行了研究。通过实验发现，随着水煤浆浓度的提高，液滴的总破碎时间会略微增大，但该规律并不是十分明显。随后，通过实验数据，拟合得到了总破碎时间随奥内佐格数的变化规律，即

Ttot=3.1(1+1.2Oh0.88)

(13)

可以发现，与高黏度牛顿流体液滴的总破碎时间相比，水煤浆液滴的破碎时间会相对较小。这是因为，只有水煤浆液滴中煤粉颗粒的大小约等于液丝尺寸时，才会表现出较强的非牛顿特性。

有关赫歇尔-布勒克利流体液滴二次雾化过程中的变形及破碎特性，现有对其的研究十分有限。宋少波[75]研究了卡波姆凝胶液滴初始变形时间随韦伯数We的变化规律。可以发现，在袋式破碎模态的临界韦伯数Wec附近，初始变形时间Tini会随着韦伯数的增大而略微上升。当卡波姆溶液的非牛顿特性较弱时，随着来流气体韦伯数的增大，初始变形时间会略微下降。然而，当卡波姆溶液的非牛顿特性较强时，尤其在高韦伯数条件下时，初始变形时间会随之上升。

3 喷嘴雾化模型在射流雾化中的应用

通过对不同种类非牛顿流体射流雾化过程的实验研究，可以观察到不同种类扰动波在射流及液滴表面的发展过程。根据初次雾化和二次雾化间的相似性，以上所得到的实验结论可以通过类比得到不同种类喷嘴所产生的液体射流在初次雾化时破碎的物理过程，结合气液界面扰动波的增长率，利用全波长积分的方法，将有关表达式代入索太尔平均直径(SMD)的定义式中进行积分，最终得到预测喷雾场中液滴平均粒径的理论表达式。这一通过理论推导得到预测喷雾场中平均粒径的物理模型被称为喷嘴的雾化模型。利用雾化模型可以对某一型喷嘴工作时所产生喷雾场的平均粒径进行计算。接下来，对现有关于不同种类喷嘴的雾化模型的研究进行综述。

3.1 低速下液体射流破碎模型理论研究

Dombrowski和Johns[77]对出口横纵比较小的扇形喷嘴进行了一系列实验及理论分析。通过与实验结果的对比，首次提出了了平面液膜的雾化模型，如图36所示。

图36 文献[77]提出的破裂模型

该雾化模型假设，当液膜上表面波振幅增长到一个临界值时，液膜波峰和波谷间的半波长液膜便会脱落下来，并在表面张力的作用下聚集成为圆柱状液丝，最终破裂并形成大量的液滴。这一模型日后被许多研究者所采纳，并基于该雾化模型计算得到平面液膜、圆环液膜等破裂过程中的特征参数(如破裂长度、液滴尺寸等)的大小。此外，Senecal等[78]的研究中也采用了相似的雾化模型。所不同的是，他们在利用质量守恒关系计算液丝直径时，由液膜破裂为液丝的过程被长波和短波区域区分开来。

Dombrowski和Johns[77]所提出的雾化模型之所以得到了广泛地应用，主要原因是该雾化模型的直观与简洁，同时在多数情况下都可以得到一个与实验吻合较好的结果。但是，在液体射流进入高速气流条件下，通过大量的实验图片可以明显地看到实验中液膜的破裂过程和Dombrowski和Johns[77]所提出的雾化模型存在着明显差异。这是由于为获得较高质量的雾化效果，液体射流往往暴露在较高速度的气体来流中。因此，通过理论方法计算高速气体扰动作用下的雾化场平均粒径更加具有实际的应用价值。

3.2 高速下液体射流破碎模型理论研究

Varga等[79]对气液面积比较大时圆柱射流在外部的高速气流作用下的破碎过程进行了一系列实验研究和理论计算。结合图37的实验观察，提出了一种基于液膜“双阶段不稳定破裂机理”的雾化模型。

图37 Varga等[79]观察到的圆柱射流下的双重不稳定破碎模式

在扰动初期，液体首先会在Kelvin-Helmholtz(K-H)不稳定波的扰动下，形成振动幅度较大并凸出液面的“液舌”结构，在液舌形成之后，其表面与来流气体的加速方向互相垂直，导致表面形成Rayleigh-Taylor不稳定波[79]。同时，假设液体射流破碎后，液滴的平均粒径与R-T不稳定波中最不稳定波的波长成正比,对液舌在气体环境中的加速度进行分析与计算，最终得到了R-T扰动波的表达式。在该雾化模型的K-H不稳定扰动中，采取了Raynal[80]论文中所提出的边界层假设，并给出了扰动波波长和气体边界层厚度之间的关系式。最终结合有关表达式所得到的正比关系得到计算液滴粒径的表达式，并与实验中所观测的结果进行对比。结果发现，实验数据与理论计算的曲线非常接近，从而佐证了该雾化模型的有效性。相似地，Aliseda等[81]将该模型的适用范围进一步地拓展到非牛顿流体射流中，同样定量地给出SMD的计算公式，进一步拓展了此雾化模型的适用范围。

Rayana等[82]在Varga等[79]所研究的基础上，进一步地验证了该模型在平面液膜雾化过程中的有效性。在平面液膜发生破碎的过程中，存在纵向及横向的两种类型的扰动波。此时R-T不稳定波处于平面液膜上，在拉伸作用下形成了纵向液丝。利用与Varga等[79]相似的理论雾化模型计算得到了SMD的表达式，同时证实在较大范围内变化的雷诺数和韦伯数下该理论模型的适用性。

对于液体射流破碎后喷雾场平均粒径的计算，研究思路均为求解最大不稳定波长，并给出SMD与波长之间的关系，再利用质量守恒关系式推算出SMD的理论表达式。然而，在理论计算中，除利用最大不稳定波长进行计算外，还可采用“全波长积分”的方式推算液滴的平均粒径，下面对该方法进行简要地介绍。Mayer[83]对圆柱射流进入高速气流中破碎后液滴的直径进行了理论推导。推导中采用了“全波长”的假设，即：假设存在一波长谱，这一波长谱下的所有振幅在激励时间内均能够快速增长到与扰动波波长的同一数量级。此时，这些伸出液面的波峰在高速气体的剪切力下从表面上剥落下来并最终形成液滴，且液滴直径正比于破裂前的波长。另一方面，通过质量守恒和全波长范围内的积分得到平均波长，进而计算得到喷雾场内液滴的平均粒径。Adelberg[84]基于Mayer[83]的破裂模型和“全波长”假设，计算了圆柱射流在高速气体下所产生液滴的平均粒径，得到了较好的计算结果。

国内有研究者对不同种类喷嘴的雾化模型进行了研究。北京航空航天大学的刘陆昊等[85]对气液同轴离心喷嘴的破碎过程进行了物理建模，将沿气体环缝流动的高速气流分解为平行于液膜和垂直于液膜两个方向的分量，气液离心喷嘴所形成液膜雾化过程的示意图如图38所示[85]。

图38 气液同轴离心喷嘴产生液膜的破碎过程[85]

可以发现，切向气流引起的切向剪切效应在液膜表面产生了K-H不稳定波，所对应的波长为λ。同时，K-H波也在液膜表面上卷起并产生了液舌的结构。液舌的厚度也和K-H不稳定波的波长成正比。切向气流分量会在液舌的迎风面一侧产生R-T不稳定波，液舌上R-T不稳定波的波长等于λRT1。同时，垂直于液膜气体速度分量在两个液舌之间的液膜上诱导产生了R-T不稳定性波。这部分R-T不稳定波的波长等于λRT2。在经历两阶段的破碎过程后，将产生大量液丝并将会从液膜上脱落下来，在表面张力的作用下收缩形成小液滴，这些小液滴所对应的特征直径为D，其大小与等效R-T波的波长是一个数量级的，即D∝λRT。最终，将所得到的扰动波表达式代入计算SMD的表达式中，利用数值积分的方法得到了计算气液同轴离心喷嘴喷雾场中SMD的半理论表达式，与实验结果进行比较，发现符合较好。

Qin等[86]建立了气助式平面液膜喷嘴的雾化模型。在研究中将平面液膜的破碎及雾化过程等效为类似于Verga等[79]所提出的双阶段破碎模型。利用全波长积分的方法，得到了预测喷雾场内液滴SMD的显式表达式，即

(14)

利用式(14),即可计算液膜破碎后，喷雾场中SMD随不同物理参数的变化规律。

近年来，Fu等[87]利用横向射流破碎后，所产生液丝与液滴之间的定量关系式，并结合SMD的定义式，得到预测横向射流破碎后下游喷雾场内SMD的理论表达式。将计算结果与实验结果进行比较，对比结果如图39所示。可以发现该雾化模型与实验符合较好。Liu等[88]结合横向射流在破碎时的质量脱落率，得到亚声速横向气流中液体射流破碎后所产生液滴的空间分布，该雾化模型所预测的平均粒径大小也与实验数据较为接近。

图39 横向射流破碎后SMD理论计算与实验对比结果[87]

可以发现，液体射流在气体中的破裂和雾化是一个十分复杂的难题。因此，工程上大多都通过大量实验数据拟合出的经验公式或半经验公式来预测雾化液滴尺寸。然而，如果能够尝试在不同工况下对液膜的破裂进行细分并给出相应简化的理论雾化模型，从而给出具有物理意义的喷雾场液滴平均粒径的理论表达式，将有助于我们对雾化过程有更加深入地理解和认识，进一步揭示相关物理现象背后所蕴含的机理。因此，对液体射流雾化理论模型的研究具有十分重要的科学及工程意义。

4 结 论

本文对有关非牛顿流体射流雾化特性的研究进展进行了综述。分别对非牛顿流体射流在初次雾化过程中表面不稳定波产生发展过程的理论与实验研究进展、非牛顿流体液滴二次雾化过程中有关变形破碎特性参数的变化规律和液体射流雾化过程在喷雾场平均粒径预测中的应用等方面进行了总结，同时对未来的研究方向进行了展望。

通过对非牛顿流体射流初次雾化有关研究内容的调研，发现对于非牛顿流体射流，因其非线性的流变特性，在预测表面波扰动增长和失稳过程的理论分析中必须考虑到流变参数对增长率的影响。理论分析结果表明，利用摄动法可以较好地预测扰动波的发展过程。当扰动波振幅进一步增大直至临近射流破裂点时，需要利用非线性稳定性分析与实验相结合的方法对液膜的破碎过程进行更深入地分析。在有关非牛顿流体射流的实验中，可以发现不同的喷注形式以及不同的喷嘴结构均会对液体射流初次雾化过程中的破碎特性产生影响，流变参数(如幂律指数、变形延迟时间等)的变化会对液体射流的破碎形态、破碎长度、喷雾锥角等参数产生重要的影响。

通过对非牛顿流体液滴二次雾化实验研究内容的调研，发现对于非牛顿流体液滴，有关其二次雾化特性的实验研究仍然较少，现有实验研究也大多集中于少数几种流体。因此，可以对更多具有不同流变特性非牛顿流体液滴的二次雾化过程进行研究。同时可以研究不同添加剂(例如表面活性剂，纳米金属颗粒，微纳气泡等)对非牛顿流体液滴二次雾化特性的影响，并对相关实验现象做出理论上的解释。同时，可以对不同种类非牛顿流体液滴破碎模态随无量纲特征数的转捩关系进行定量地计算与讨论。

此外，可以通过对液滴二次雾化过程的实验观测，研究不同种类液滴在发生二次雾化后，所产生小液丝或液滴尺寸分布随流场参数的变化规律，建立非牛顿流体射流破碎的雾化模型。以上所展望的方向都是可以在未来进行深入研究和讨论的。