基于ADAMS与AMESim的飞行器发射动力学仿真

赵君伟，张家骏，张 程，司世才，裘群海

(中国运载火箭技术研究院, 北京 100076)

0 引言

战役战术导弹常以发射箱/筒作为其发射装置，发射过程中导弹与发射装置的安全间隙及导弹出箱之后的初始姿态是发射过程中关注的两大核心问题。发射动力学是研究飞行器在发射时的受力和系统响应特性，进而研究飞行器控制受力和运动规律的理论、技术和试验测试的方法。通过对发射动力学进行研究，寻求起始扰动和系统振动特性的计算方法，分析影响起始扰动和系统振动的主要因素，进而为飞行器的设计、试验及性能改进提供技术手段，提高飞行器作战效能。近20年来，随着计算机仿真技术的飞速发展，虚拟样机技术开始广泛应用于发射动力学仿真计算中。虚拟样机技术又称为机械动态仿真技术，是一种融合了现代信息技术、先进仿真技术、先进制造技术并将其应用于复杂系统的全生命周期综合管理中，支持由上至下的复杂系统的开发模式，利用虚拟样机技术代替物理产品进行性能评估和测试，对缩短产品开发周期、降低产品研发成本具有十分显著作用[1-3]。

1 某型飞行器物理模型

某型飞行器全长7 m，最大直径为400 mm，长细比达17.5，飞行器采用三排翼气动布局方案，箱式倾斜热发射方案发射出箱，发射箱起竖过程通过液压缸实现，在发射箱起竖至预定角度后，伺服阀锁闭使得发射箱保持在当前角度。发射车简化模型如图1所示，飞行器模型如图2所示。

图1 某型飞行器发射车模型

图2 某型飞行器物理模型

飞行器在箱内通过滑块形式与发射箱内的导轨接触配合，在飞行器出箱过程中起导向作用。因发射箱内空间限制，翼舵在箱内呈折叠状态，通过发射箱内壁的翼轨对翼舵进行约束，三排翼在出箱后展开。飞行器主要结构参数如表1所示。

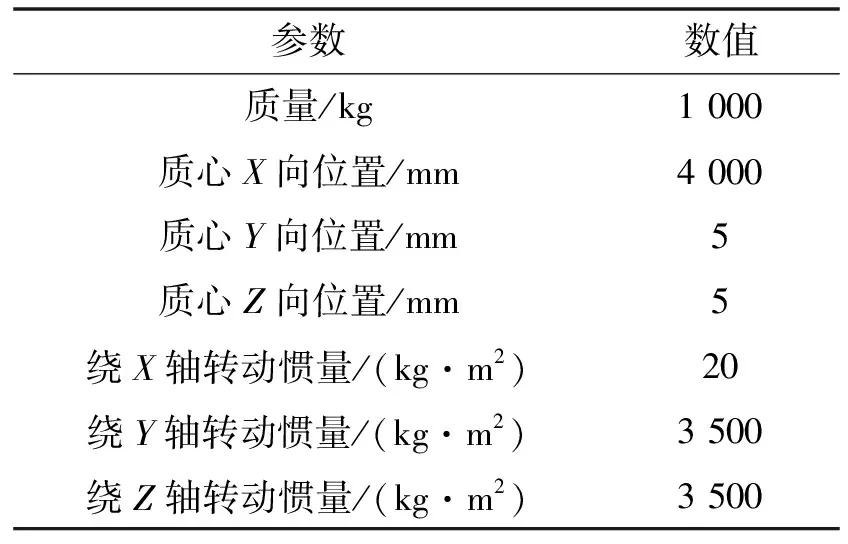
表1 飞行器质量特性

2 ADAMS多体动力学仿真原理

动力学仿真软件ADAMS采用多体动力学中的拉格朗日方法建立多体系统的动力学和运动学方程[4]。

ADAMS软件在惯性空间中定义了一个全局坐标系(ground)，在刚体Bi(i=1,2,…,n)的质心上定义了一个随体坐标系(body)，并且刚体质心的3个笛卡尔坐标x,y,z表示位置，欧拉角ψ,θ,φ表示姿态：

(1)

ADAMS所采用的笛卡尔广义坐标qi就是上式变量的集合：

(2)

笛卡尔广义坐标系下，全局坐标系下各个刚体质心的线速度vi、角速度ωi和角加速度ξi可以表示为：

(3)

(4)

(5)

其中

(6)

那么，刚体上任一点K的位置、速度和加速度矢量方程形式如下：

ri=ui+hi

(7)

(8)

(9)

式中hi为K点相对于随体坐标系原点O的矢径。

(10)

角速度矢量在随体坐标系下的坐标列阵ω′为：

(11)

其中

G′=[sinθcosφ-sinφ0]

(12)

将式(12)代入式(11)，可得系统动能的欧拉角表达式为：

(13)

ADAMS采用的多体系统动力学方程是由整个系统各个刚体的带乘子的拉格朗日方程和系统所有的约束方程组成：

(14)

式中：T为系统动能；Q为广义力列阵；λ为对应于完整约束的拉格朗日乘子列阵；μ为对应于完整约束的拉格朗日乘子列阵。

3 ADAMS机械子系统仿真模型

在采用ADAMS软件分析时，遵循如图3所示基本步骤。

图3 ADAMS机械动力学软件仿真分析步骤

对于复杂的三维实体模型，采用ADAMS软件进行建模难度较大，若使用现有三维建模商业软件进行模型创建后导入不仅大幅降低工作难度，也可保证模型几何精度[5]。考虑翼舵折叠动作、翼与发射箱之间的接触碰撞、适配器与发射箱之间的碰撞与发射动力学计算结果有直接影响，本次计算模型中前翼、中空气舵和后翼在Creo Parametric 2.0软件创建的模型基础上进行简化，取消内部折叠展开机构的结构件，只保留翼舵的主要部组件，折叠动作采用ADAMS软件中约束进行定义；飞行器结构体、适配器根据理论外形进行直接建模；发射箱模型根据理论外形进行直接建模，发射箱内外壁尺寸及高度与实际模型保持一致，不考虑内部燃气腔结构。

建立上述模型时，为研究方便，有以下几个假设：

1)各运动副的摩擦力按照材料的摩擦系数设置；

2)各运动副均为刚性连接，内部间隙不计；

3)所有运动体均为刚性体。

根据受油机运动模拟系统实体设计及材料选型，为ADAMS模型添加包括预紧力、重力、摩擦力在内的约束力。其中，螺栓预紧力、摩擦力通过查询机械设计手册得到，系统重力加速度为-9.806 65 m/s2。

ADAMS与AMESim间的仿真接口由ADAMS/Controls提供。ADAMS模型与AMESim间的数据交互通过ADAMS中设置的接口状态变量进行传递。其中，ADAMS模型共设置接口变量3个，包括有液压缸输出力、位移、角度等。仿真接口变量设置情况见表2。

表2 仿真接口变量设置情况

在开展仿真过程中，考虑的偏差条件主要包括：

1)X,Y,Z方向转动惯量偏差，负偏差10%；

2)Y,Z方向偏心量均为10 mm；

3)Z方向风干扰，风速大小为±20 m/s。

风载为地面水平风，为简化仿真工作，风载荷取常值风速+20 m/s，风载荷大小与飞行器露出发射箱的面积成正比。将风载转化为集中力作用于出箱后的飞行器，由于飞行器出箱的部分是变化的，承受风载的面积也就变化，风载作用力的大小和数值也就是变化的。为了便于计算将风载作用力作用点移至飞行器顶点，作用力大小不变；根据力的平移原理施加等效力矩，符合右手定则。转化后风载荷作用力和作用力矩分别如图4、图5所示。

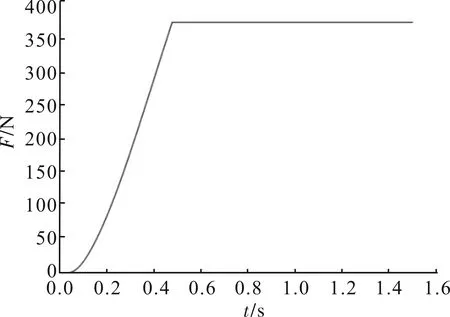
图4 飞行器顶点风载荷作用力

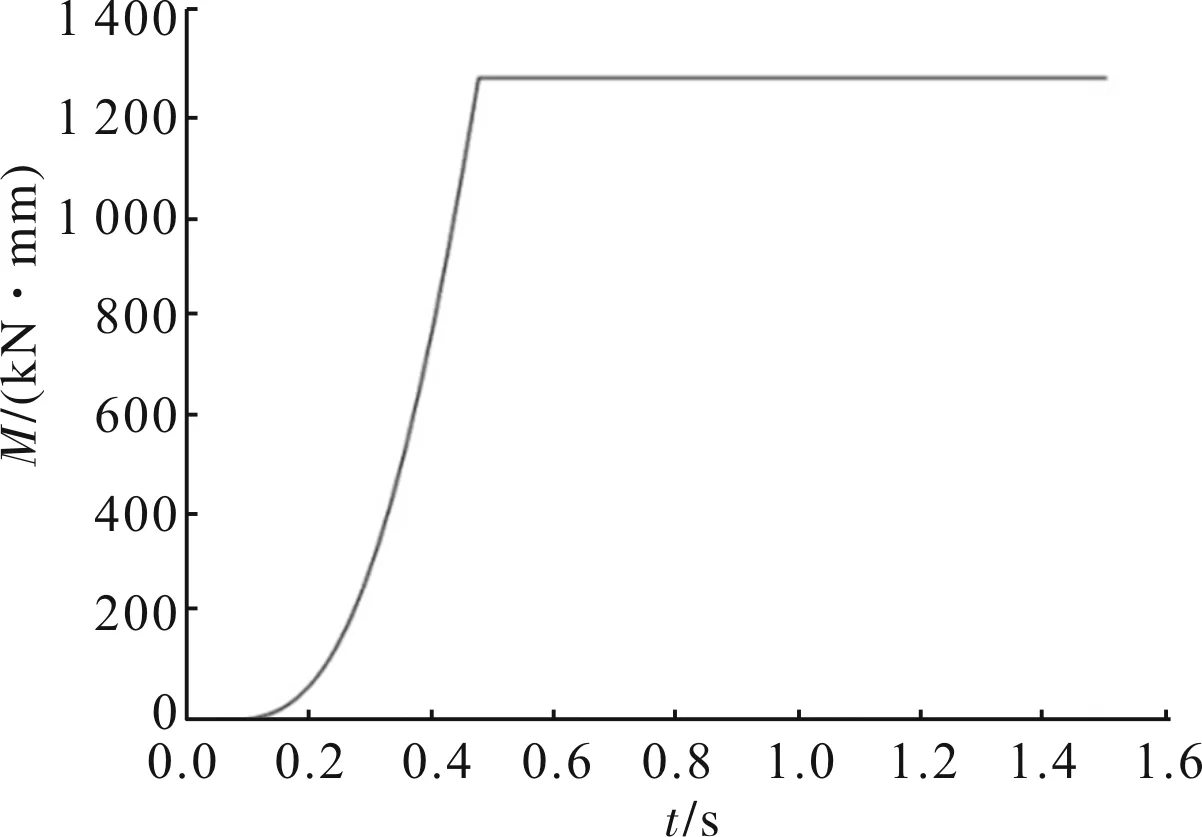
图5 飞行器顶点风载荷作用力矩

4 AMESim液压子系统仿真模型

发射车弹体支撑系统由阀控液压缸伺服系统控制，其具有构造简单、占用空间小、承载能力大、结构紧凑的特点。电液位置伺服系统由伺服阀、伺服放大器、非对称液压缸、比例加法器、位移传感器和负载等构成。其中，伺服放大器传递函数为：

I=KaΔu

(15)

电液伺服阀传递函数可近似视为二阶振荡环节，其传递函数为：

(16)

推导阀控非对称液压缸传递函数时，假设1)阀可视为理想的零开口四通滑阀，具有理想的响应能力。2)液压缸为理想的单出杆液压缸，各腔内液压力各处相等，体积弹性模量与油液温度视为常数，内外泄漏流动为层流。3)系统管道短且粗，管道中摩擦损失、流体质量以及管道动态特性忽略不计。

阀控非对称液压缸中，由于其有杆腔和无杆腔面积的不等，导致液压缸在正反两方向运动过程中传递函数不一致，需要分别求解。

(17)

定义负载流量qL：

(18)

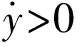
qL=Kq1xv-Kc1pL

(19)

式中:

其中：cd为伺服阀阀口流量系数；w为伺服阀节流口面积梯度。

无杆腔流量连续性方程为：

(20)

有杆腔流量连续性方程为：

(21)

由液压缸力平衡方程，有：

(22)

进行拉普拉斯变换，得系统传递函数为：

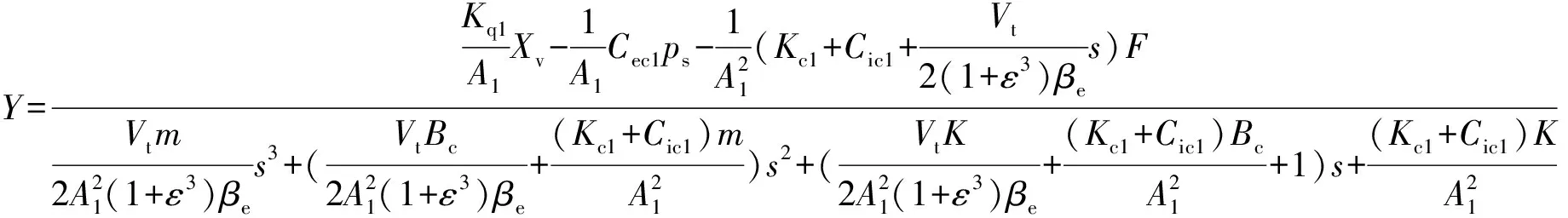
进一步化简，有：

(23)

式中：

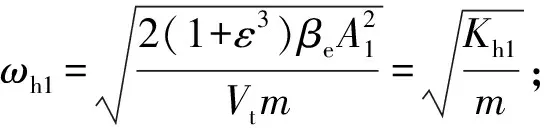
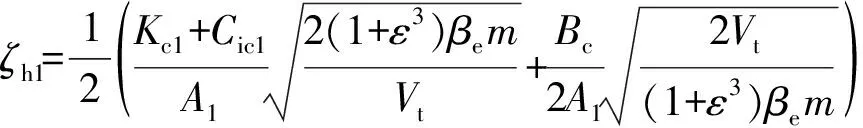
同理求解得到传递函数表达式为：

(24)

式中：

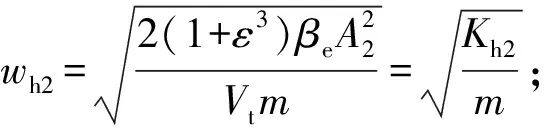
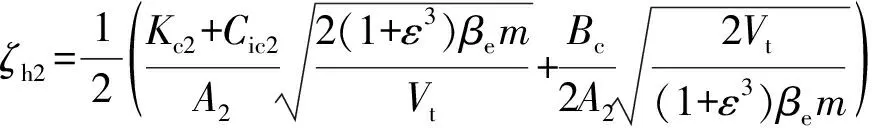
注意，表达式中Kc2，Kq2，Cic2，Cec2与Kc1，Kq1，Cic1，Cec1不同，具体为：

由式(23)和式(24)可知，阀芯位移xv>0和阀芯位移xv<0具有相同形式的传递函数，则系统传递函数方框图可表示为图6形式。求解得到电液位置系统传递函数如式(25)。

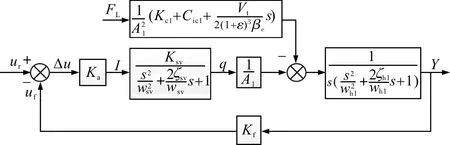
图6 阀控非对称液压缸电液位置伺服系统传递函数

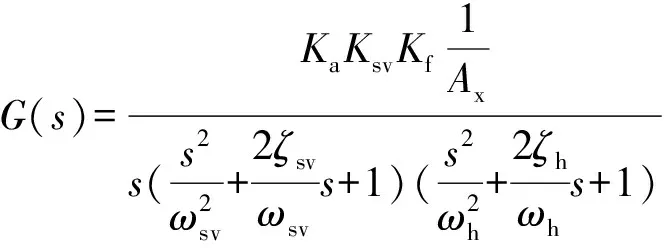
(25)

根据系统设计及选型，总结阀控非对称液压缸伺服系统动力机构参数如表3所示。

表3 阀控非对称液压缸伺服系统动力机构参数

以升降运动电液位置伺服系统为例，求解系统在阀芯位移xv>0和阀芯位移xv<0下的开环传递函数。

当阀芯位移xv>0时，

(26)

当阀芯位移xv<0时，

(27)

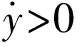
基于AMESim软件建立发射车液压子系统模型如图7所示，其中AMESim与ADAMS仿真接口共包含3项变量，ADAMS输出至AMESim变量为发射箱倾斜角度angleout和液压缸伸缩距离displacement，AMESim输出至ADAMS变量为液压缸输出作用力[6-7]。

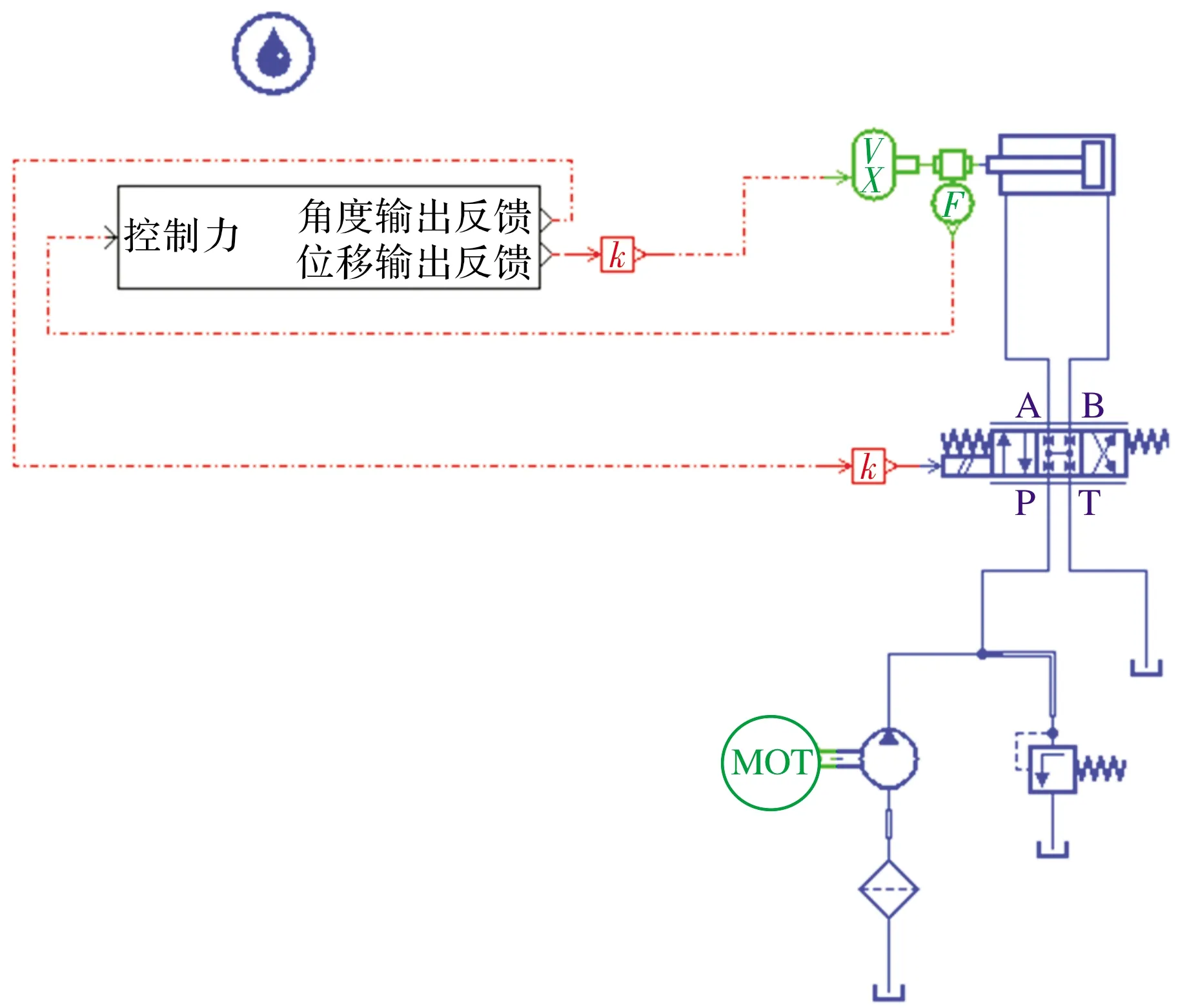
图7 AMESim中建立的发射车液压子系统模型

5 仿真结果分析

利用基于ADAMS与AMESim联合仿真分析方法对飞行器出箱过程进行仿真分析，其偏航、滚转、俯仰角度、角速度，X、Y、Z方向位移及速度随时间变化情况如图8～图12所示。

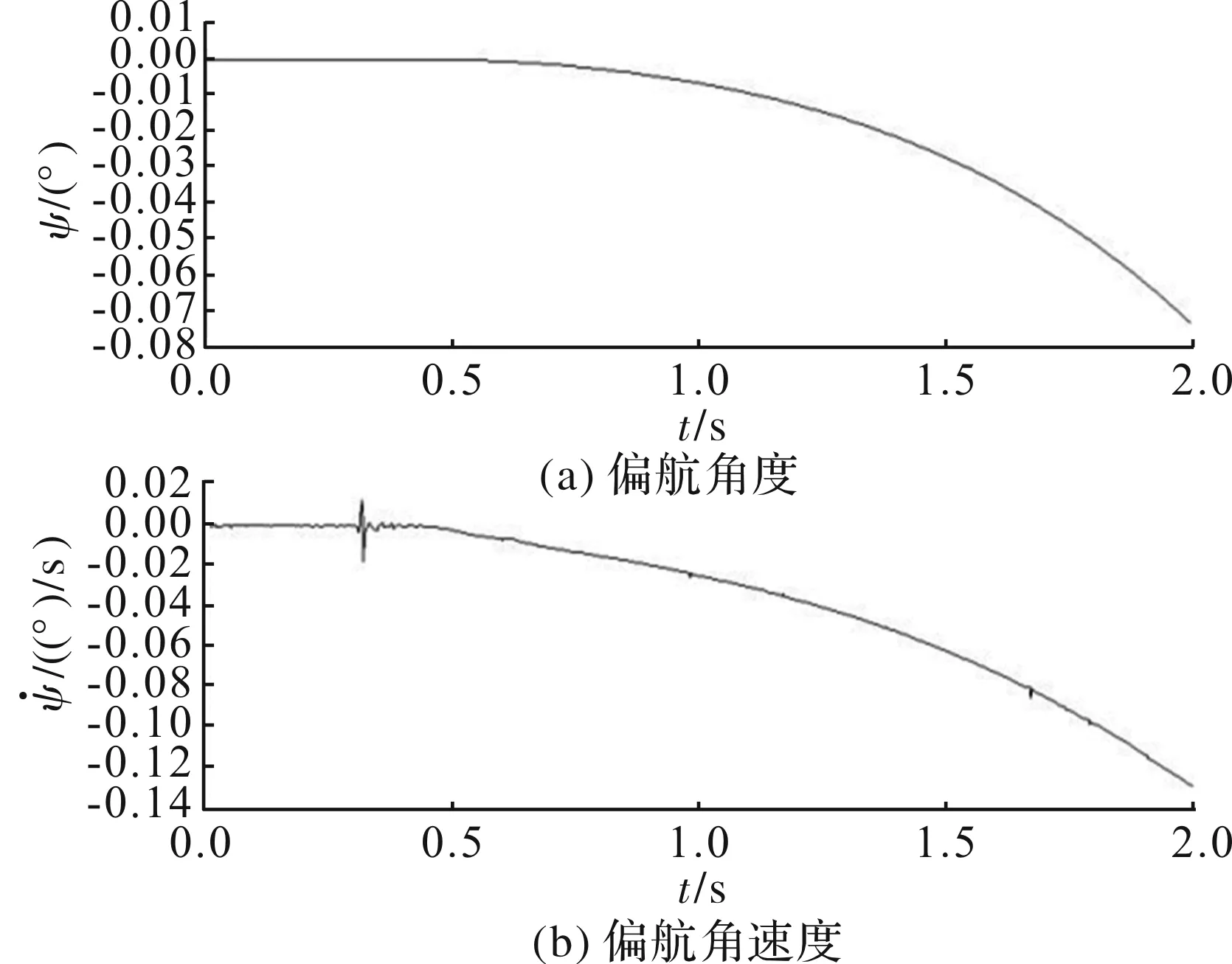
图8 偏航角度及角速度随时间变化

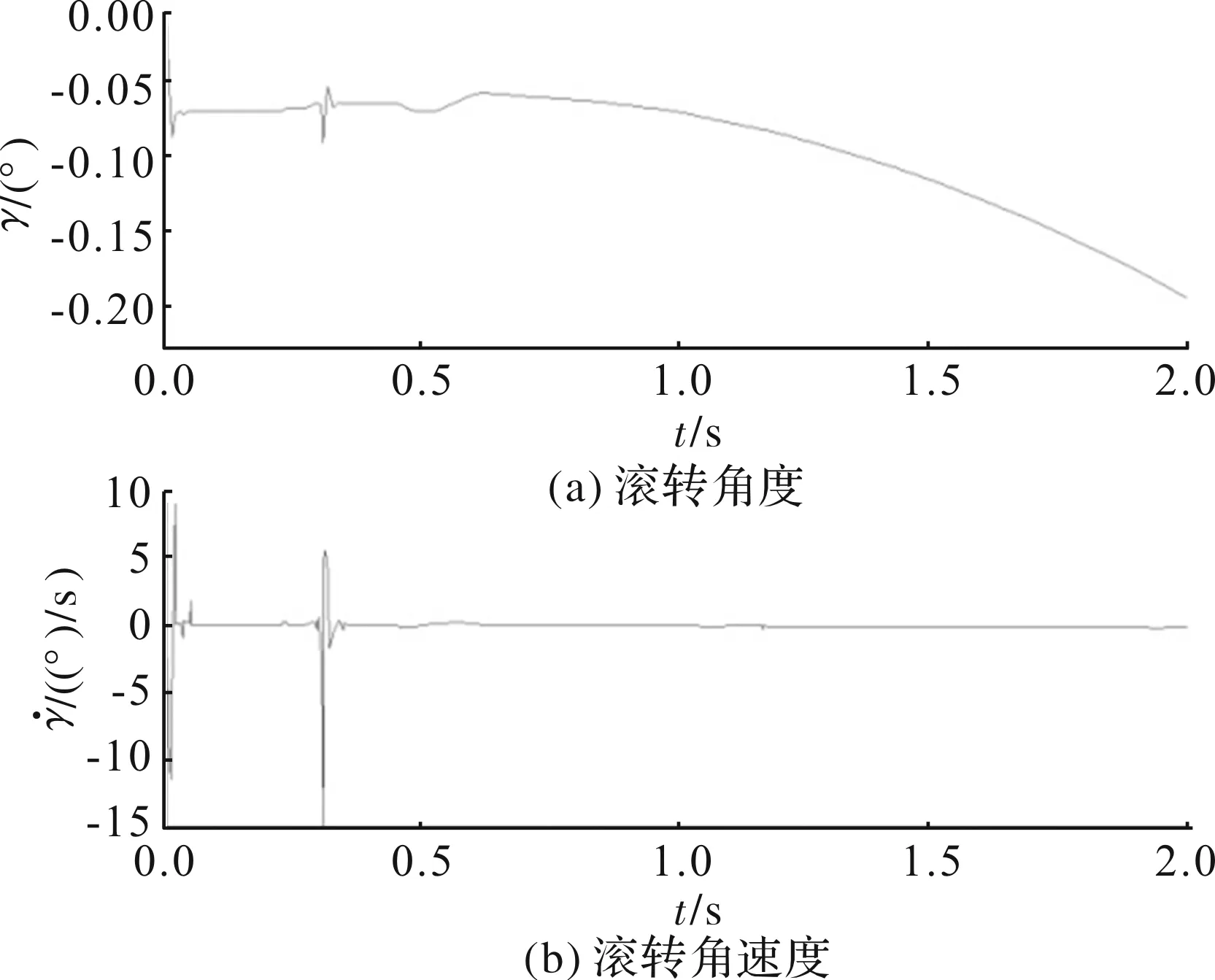
图9 滚转角度及角速度随时间变化

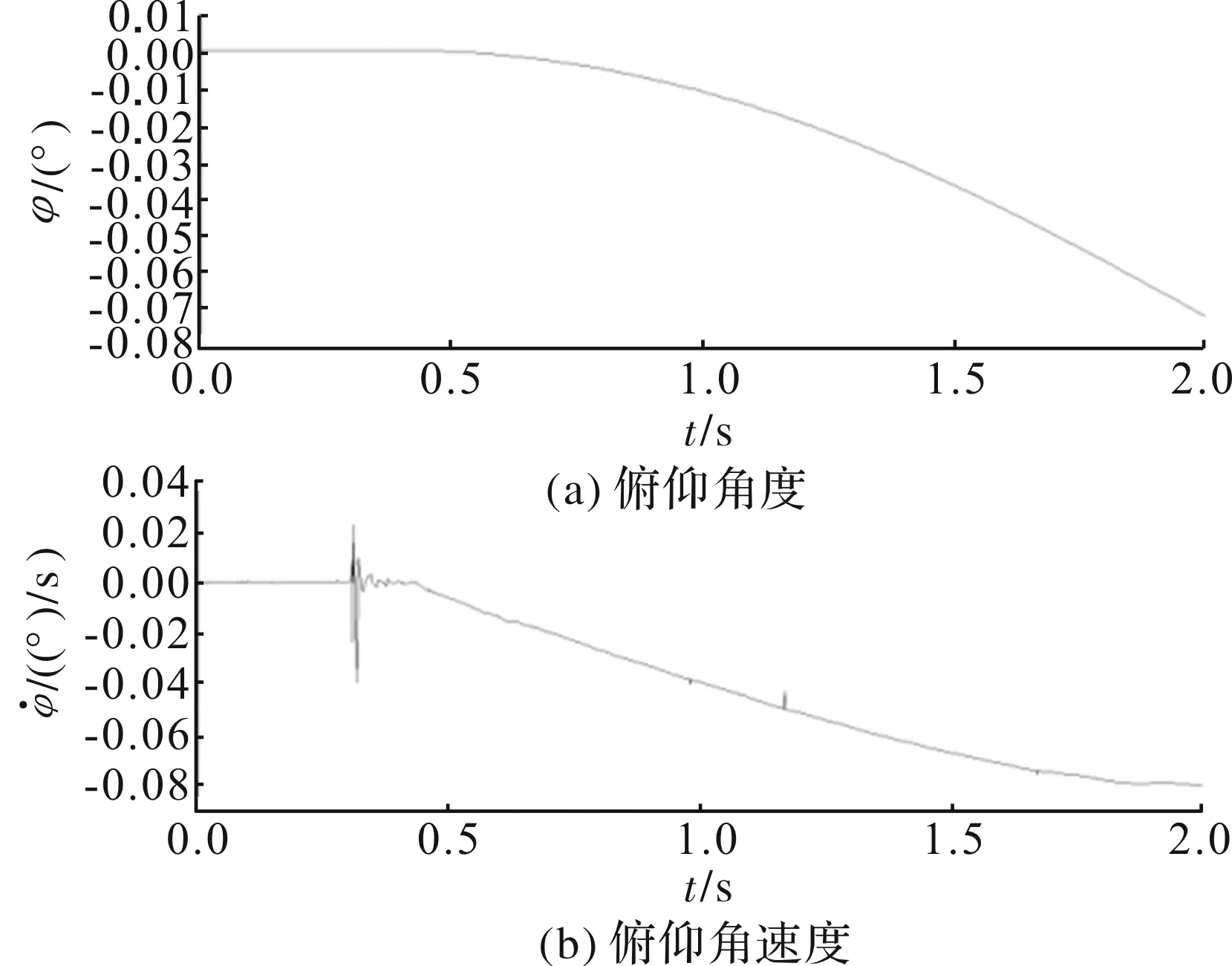
图10 俯仰角度及角速度随时间变化

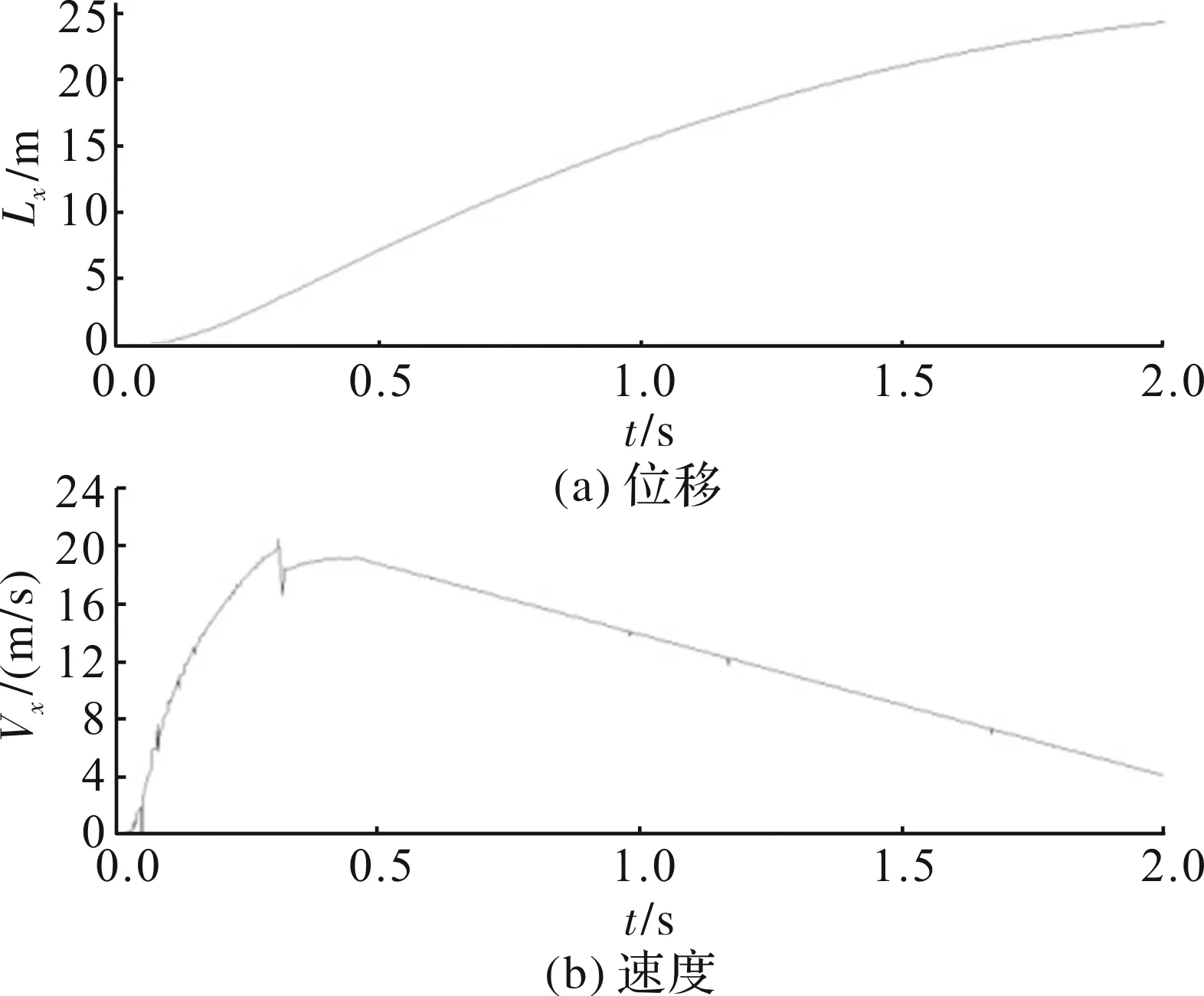
图11 X方向位移及速度随时间变化

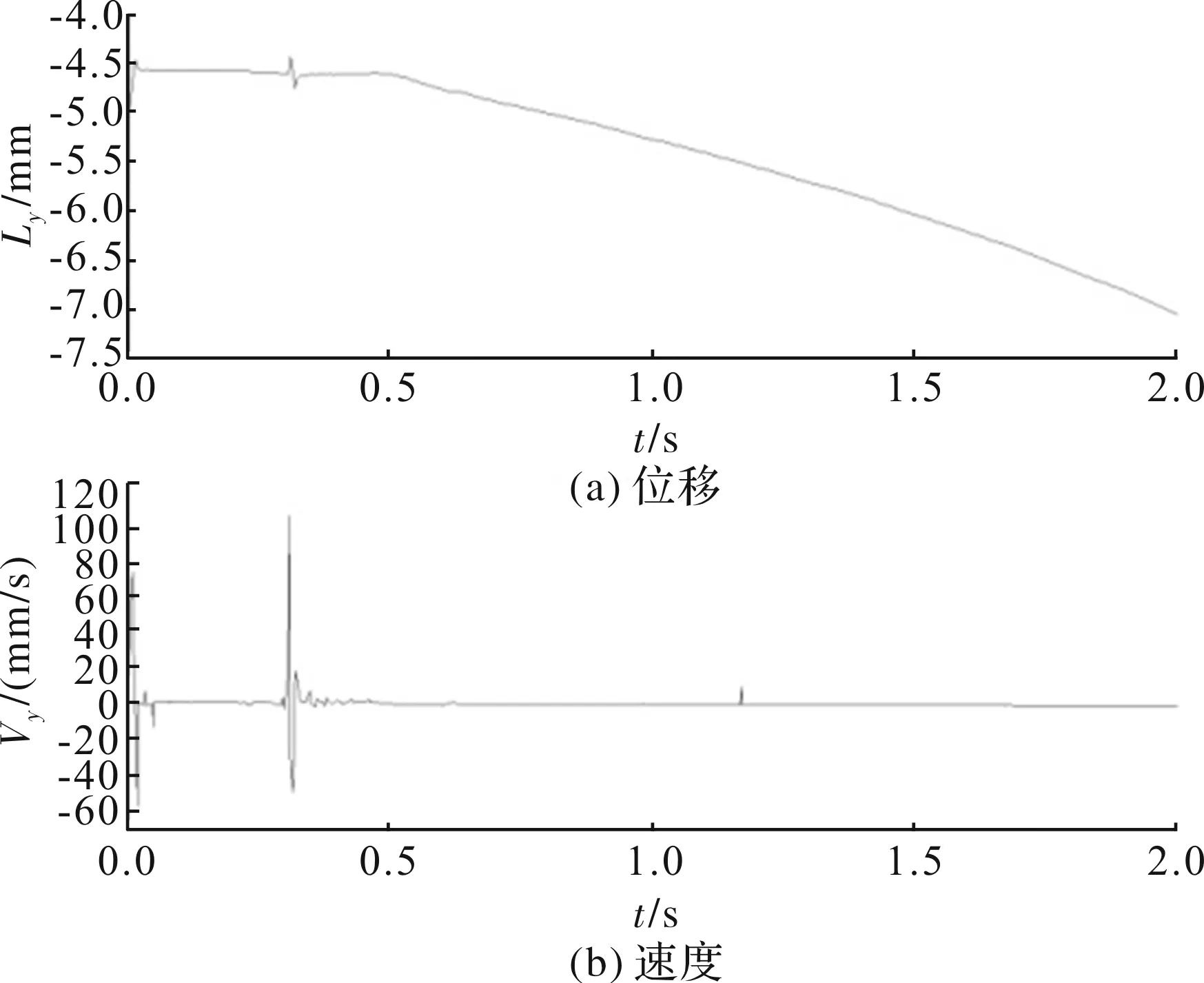
图12 Y方向位移及速度随时间变化

通过对仿真结果进行分析，飞行器发射出箱2.0 s后姿态统计结果如表4所示。

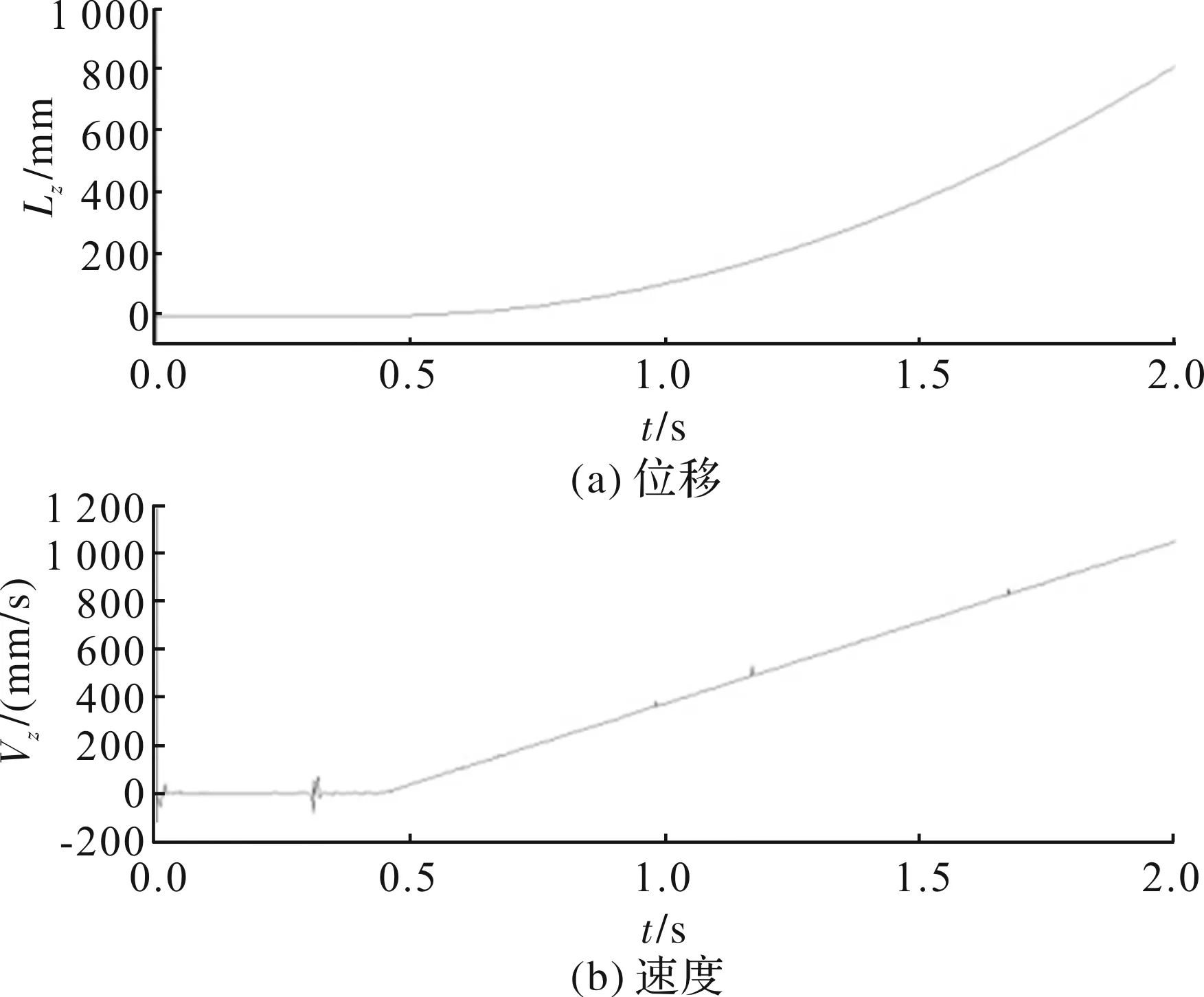
图13 Z方向位移及速度随时间变化

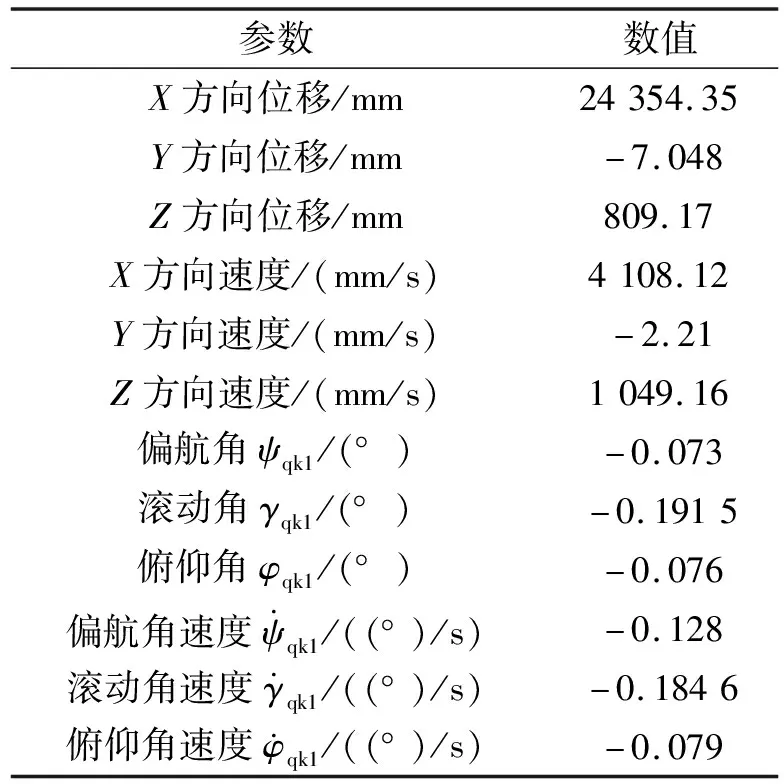
表4 统计2.0 s姿态仿真结果

由仿真结果可以看出，飞行器在出箱后，俯仰、偏航角度及角速度较小，滚转方向角度和角速度较大。

6 结论

采用基于AMESim和ADAMS联合仿真分析的方法对某型飞行器发射过程进行仿真分析，充分考虑叠翼舵、滑块与发射箱导轨碰撞和摩擦，风干扰、质量偏差以及发射车液压系统动态特性。经仿真分析，飞行器出箱2.0 s后偏航角度、俯仰角度及偏航角速度、俯仰角速度数值较小，滚转角度和滚转角速度受翼舵折叠及展开影响，数值相对翼舵不断叠状态有所提高。飞行器均能正常起控，符合设计要求。