基于加权平方误差损失函数的鲁棒TOA源定位算法

2022-01-10弓艳荣

弹箭与制导学报 2021年5期

弓艳荣，刘鹏

(内蒙古电子信息职业技术学院，呼和浩特 010070)

0 引言

源定位技术是通过发射端发射信号，接收端通过测量信号的到达时间(time of arrival, TOA)[1]、接收信号强度(received signal strength, RSS)[2]以及到达角度等参数，估计发射端位置的技术。

目前，针对非视距(non-line-of-sight, NLOS)和视距(line-of-sight, LOS)的混合(LN-M)场景下的源定位算法[2-6]可分为基于优化的约束最小二乘法和基于稳健统计定位两类。前者具有较高的定位精度，但它的复杂度高于基于稳健统计定位算法。因此，文中着重关注基于稳健统计定位算法。

多数的LN-M场景下的源定位算法采用中值概念，如最小中值平方(least median squares, LMEdS)[7]，M-估计[8-9]等。但测距信号的抽样值在正态分布条件下，抽样均值(sample mean, SMN)是一个有效估计策略，其性能优于抽样中值(sample median, SMIN)策略。

然而，当出现异常抽样值时，即抽样值服从t分布、双重指数分布等重尾分布时，抽样均值的准确性迅速下降，劣于SMIN。因此，将基于抽样均值的加权平方误差(weighted square error, WSE)损失函数用于LOS场景。相反，在LN-M场景下就采用基于抽样中值的WSE损失函数。因此，通过最小化这两个场景下的WSE损失函数的和可实施源定位。为此，提出加权平方误差损失函数的鲁棒定位算法WSE-RS。

1 源定位的形式化表述及预备知识

假定网络内有M个接收器(传感节点)，一个发射器(源节点)。令[xiyi]T为第i个传感节点的位置,[xy]T为源节点位置。

接收端通过测量源节点传输信号的到达时间TOA可估测与源节点的距离。在LOS/NLOS混合环境下，可建立式(1)所示的测量等式。第i个接收器所测量到源节点的距离为：

(1)

式中：di表示源节点(发射器)与第i个接收器间的真实距离；ni,j表示对噪声变量的第j个抽样值[10]。且i=1,2,…,M;j=1,2,…,P。ni,j服从LOS和NLOS的高斯混合分布，可表示为：

(2)

1.1 基于抽样中值的最小二乘估计

用最小二乘法[11]求解式(1)。对式(1)两边平方，可得：

(3)

AX+qj=bj

(4)

ri,j中的异常值严重降低了算法性能。因此，用中值滤除异常值的影响。利用最小化平方误差和实现LS定位估计：

(5)

式中：med(b1:P)=[med(b1,1:P),med(b2,1:P),…,med(bM,1:P)]T。med()表示计算中值的函数，即对P个抽样值进行排序，取中间值。例如，med(b1,1:P)表示计算b1中P个抽样值的中值。传统的LS估计是计算所有抽样值的平方误差和，而式(5)是计算节点抽样值中值的平方误差和。

1.2 基于抽样中值的高斯-牛顿估计法

采用高斯-牛顿估计法进行源定位。先建立最小化平方误差的表达式：

(6)

再利用泰勒级数展开算法在参考点x0处对测距值进行线性处理：

d=f(X)≈f(x0)+G(X-x0)

(7)

(8)

利用基于抽样中值的LS估计位置作为x0，可对X进行估计：

X(k+1)=X(k)+(G(k)TG(k))-1G(k)T[med(r1:P)-f(X(k))]

(9)

式中：X(k)表示第k次迭代的X估计；med(r1:P)=[med(r1,1:P),med(r2,1:P),…,med(rM,1:P)]T。

2 WSE-RS算法

将LOS/NLOS的混合场景划分为LOS场景、LOS/NLOS场景。ε=0表示LOS场景；0<ε≤1表示LOS/NLOS场景。当传感节点处于LOS/NLOS场景时，就利用抽样中值构建损失函数；当传感节点处于LOS场景，就利用基于抽样均值构建损失函数。

2.1 LOS场景与LOS/NLOS场景的识别

(10)

2.2 基于抽样均值的WSE损失函数

当节点处于LOS场景，WSE-RS算法就利用抽样均值构建WSE损失函数：

(11)

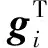
将式(11)扩展到多个节点得：

(12)

式中：NLOS表示属于LOS节点的下标集。

2.3 基于抽样中值的WSE损失函数

当节点处于LOS/NLOS时，WSE损失函数为：

(13)

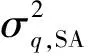
2.4 基于高斯-牛顿的LN-M场景下的位置估计

分别计算出在LOS、LOS/NLOS场景下的WSE损失函数，并通过最小化这两个损失函数之和，实现对源节点定位：

(14)

通过求解式(15)可得源节点X的估计：

(15)

图1给出WSE-RS算法估计源节点位置的简要过程。先识别场景，再分别计算两个场景下的损失函数，最后依据式(15)估计源节点位置。

图1 WSE-RS算法框架

3 性能仿真

在Windows 7操作系统、8 GB内存、core i7 CPU的PC上进行实验仿真。利用MATLAB软件建立仿真平台。在20 m×20 m区域内部署7个传感节点，一个节点位于区域中心，另6个传感节点分别分布于区域的边界上，如图2所示。10个源节点随机分布于区域内。节点的通信半径为10 m。

图2 7个传感节点和10个源节点的部署

选择基于抽样中值的最小二乘估计(LS-SM)和基于抽样中值的高斯-牛顿估计(GN-SM)作为参照，并分析它们的均方根误差RMSE的平均值，其表达式为：

(16)

3.1 LOS噪声的标准方差对ARMSE的影响

首先，分析LOS噪声的标准方差σ1对ARMSE的影响。σ1变化范围为0.5～4，ε=0.3，σ2=10，μ2=5。仿真结果如图3所示。

图3 LOS噪声的标准方差σ1对ARMSE的影响

从图3可知，方差σ1的增加，增加了MSE的均值。原因在于：方差σ1测距误差越大，降低了定位精度。相比于LS-SM算法、GN-SM算法，提出的WSE-RS算法降低了定位误差。这是由于WSE-RS算法通过损失函数识别LOS场景和LOS/NLOS场景，并利用最小化两个场景下的损失函数之和，估计节点的位置。

3.2 NLOS噪声的标准方差σ2对ARMSE的影响

分析σ2对ARMSE均值的影响，其中σ2从2至10变化，如图4所示。

图4 NLOS噪声的标准方差σ2对ARMSE的影响

从图4可知，提出的WSE-RS算法的定位精度仍优于LS-SM算法和GN-SM算法。LS-SM算法的定位精度最差，原因在于：LS-SM算法只通过最小二乘估计源节点位置，并没有考虑到LOS场景与LOS/NLOS场景的区别；而GN-SM算法是在LS-SM算法的基础上进行迭代，定位精度得到提高。此外，对比图4(a)和图4(b)不难发现，图4(b)的定位精度劣于图4(a),有两个原因：1)ε越大，意味着发生LOS/NLOS场景的概率越大，测距精度越低；2)σ1的增加，加大了测距误差。