基于分形维数的自适应窗口DAVAR改进算法

王梓帅，刘 星，闫 曌，杨银芳，喻 佩

(1 西安工业大学电子信息工程学院，西安 710021；2 西北工业集团有限公司，西安 710043；3 西安北方光电科技防务有限公司，西安 710043)

0 引言

目前微机电(MEMS)陀螺传感器多用于惯性导航技术中角速度的测量，在低精度军用、民用领域有广泛应用。但相对光纤陀螺、激光陀螺精度较低，需要采用Allan方差[1-4]及其拓展动态Allan方差[5-6]、交叠式Allan[7]方差等方法，对陀螺输出信号进行误差辨识，为下一步滤波提供依据。

动态Allan方差(DAVAR)最初是一种分析原子钟时变稳定性的工具，其本质是通过使用窗函数在不同的时间间隔内计算Allan方差，最终将得到的结果绘制在三维图形内进行分析。但由于窗函数的长度缺乏灵活性，在信号追踪能力和方差置信度无法兼顾[8]，会对分析的结果产生诸多弊端。汪立新等引入截断窗内峭度值，并建立以峭度为变量的自适应窗函数[9]；杨浩天等提出了一种σ2作为判据动态调整自适应窗函数截取信号[10]；张娜等提出窗函数组合法和噪声量值二维表示法对DAVAR进行改进[11]，但依然不能精确评估各噪声的变化特征。

针对传统DAVAR法存在的不足，文中提出一种基于分形维数调整窗长的改进DAVAR算法。

1 Allan方差理论及分形维数

1.1 Allan方差原理

(1)

取不同τ下的σ2(τ)绘制成Allan方差曲线。

1.2 误差模型

如表1所示，不同功率谱密度分布的噪声会在Allan方差中以不同分量形式体现，即可辨识随机误差的各类噪声项。

表1 MEMS陀螺随机误差项Allan方差特性

假设各噪声源统计独立，则Allan方差拟合模型可表示为：

(2)

1.3 分形维数计算与判据

分形理论从时间序列数据中研究复杂非线性问题，是描述信号无序程度和复杂度的无量纲指标[12]。对于噪声信号，分形维数越大表明该信号复杂度和非平稳性高，越小表明信号越单一且具有规律性[13]。常见的分形维数计算方法有[14]：计盒维数法、关联维数法、Hurst指数法、小岛法、半方差法[15]等。

测量时间序列得到z(t)，其半方差为：

(3)

式中:j为测量时间序列号;Δt为间距。对于分形曲线，存在Δt与r(Δt)的幂值关系r(Δt)∝Δtp，其中p为幂指数，将Δt与r(Δt)绘制到双对数曲线中，回归后，可以得到其斜率为p，则分形维数值为：

(4)

根据分形维数的定义，当信号发生较大的波动时，区间分形维数增大，D值不断增加。因此可以将D值作为检测突变信号的判据，根据D值的变化来实时表征信号突变特征。

2 DAVAR的窗函数设计

DAVAR是在Allan方差的基础上，利用滑动窗函数原理，在不同相关时间内利用矩形窗函数截断输出数据，重复估计Allan方差，将结果绘制在三维图形中，对信号的评定不再局限于二维曲线中。

窗函数长度的设计，影响算法跟踪动态噪声的快慢。短窗口内数据少，跟踪及时，但会导致方差的置信度降低；长窗口利于计算，估计置信度越高，但抗干扰能力弱，无法及时跟踪突变。

以D值为判据设计改进窗长函数为：

(5)

(6)

通过改进窗长函数，能保证随着信号的突变程度来实时改变窗口长度。

3 D-DAVAR改进算法设计

以分形维数为依据的D-DAVAR算法具体步骤如下：

1)对随机信号z(t)，时间起始点设为t1。

2)z(t)被中心点t1、起始宽度为W(t1)的窗函数截断，获得窗口截断信号yW(t1)，支撑变量t′描述窗内渐逝的时间为：

(7)

长度W(t)的矩形窗函数PW(t)定义为：

(8)

则截取信号为：

yW(t1,t′)=y(t′)PW(t1-t′)

(9)

3)根据式(4)计算截断信号yW(t1,t′)的D(t1)，按照式(5)确定下一时刻窗长。

4)建立一个增量过程,Δ(t1,t′,τ)定义为截断信号yW(t1,t′)与Allan窗口hτ(t′)的卷积：

(10)

其中：

(11)

参数0<τ≤τmax,τmax是最大观察间隔，通常取τmax=W/3，则可以定义为：

(12)

将t1时刻动态Allan方差定义为总体平均值：

(13)

式中〈〉为求总体平均符号。

5)通过最小二乘法，即可拟合分离出当前时刻陀螺的各项噪声系数。

7)将结果绘制在三维图中。

4 仿真及结果分析

为了验证文中提出的改进方法，采集某MEMS陀螺动态输出信号，预处理后采样4 000个数据，采样周期20 ms，输出信号如图1所示，图中z(t)代表MEMS陀螺动态输出。

图1 陀螺仪输出信号

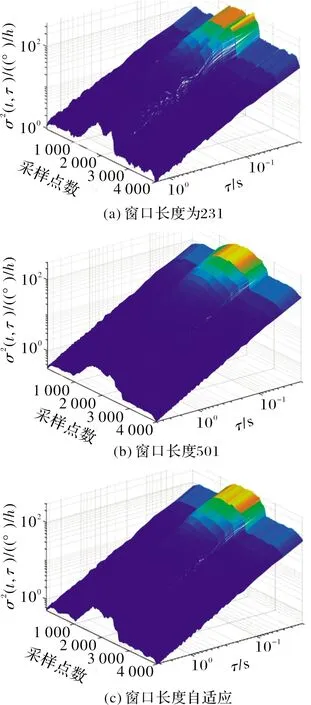
图2 不同窗口长度的DAVAR分析

由图2可看出：改进方法将长短窗口的显性优势结合，信号突变处较好的反映其特性，在平稳处也表现较为平滑。

在改进DAVAR算法中，D值与窗口长度的变化过程如图3、图4所示。

图3 D值变化过程

图4 窗口长度变化过程

不同窗口长度下对突变信号的跟踪能力如表2所示。

表2 突变位置比较表

由表2可以看出，自适应窗长的改进方法在跟踪信号突变能力上相比短窗口表现较好，且优于长窗口。

通过最小二乘拟合分辨出主要影响陀螺精度的噪声系数。角度随机游走N和零偏不稳定性B在不同窗长下随时间变化的趋势如图5所示。

图5 主要噪声在不同窗口长度的DAVAR分析

由5图可看出：在突变处及时跟踪到了信号的突变，并提高了信号置信水平。

各项噪声系数均值表如表3所示，可以清晰地看出改进的方法表现较好。

表3 噪声系数估计均值

5 结论

在DAVAR算法基础上提出一种基于分形维数调整窗长的改进算法，对陀螺输出数据进行处理。仿真实验结果表明：该方法可较准确的跟踪和描述非平稳信号，以较高的置信度对弹载环境下噪声进行辨识，有利于惯性器件误差的建模与分析，为下一步滤波提供依据。