基于互相关处理和分数阶傅里叶变换的高机动目标检测算法研究
2022-01-10庞存锁郭华玲
庞存锁,张 硕,郭华玲
(1 中北大学信息与通信工程学院,太原 030051;2 中北大学信息探测与处理山西省重点实验室,太原 030051;3 中北大学电子测试技术国家重点实验室,太原 030051;4 中北大学电气与控制工程学院,太原 030051)
0 引言
随着技术的发展,越来越多的飞行器具有高速、高机动、隐身等特点,这给常规的雷达探测带来了大的挑战。在相同的观察时间下,高机动目标的回波积累能量较常规目标低,为了提高目标的检测概率,常用增加积累时间的方法进行相参积累[1-6]。目前,长时间相参积累方法主要有两大类:一类是基于参数联合搜索方法[3,7-13],一类是基于降阶处理的互相关参数估计方法[14-18]。其中,文献[3]研究了基于MLE(maximum likelihood estimator)的距离、速度、加速度参数估计方法,并利用克拉美-罗下界进行了参数误差分析。文献[7]研究了基于KT(keystone)方法的距离走动补偿方法,但对速度较大的目标存在速度模糊数。文献[8]研究了基于RFRFT(radon-fractional fourier transform)的高机动目标检测方法,利用Radon变换和FRFT分别完成距离走动补偿和多普勒频率走动补偿。文献[9]研究了基于TDST(three-dimensional scaled transform)的高机动目标检测方法,输出信噪比较动目标检测方法提高10 dB以上。文献[10]研究了基于Radon变换的距离走动补偿和基于LVD(Lv’s distribution)的多普勒频率走动补偿方法,检测性能接近RFRFT。文献[14-16]分别研究了基于DPT(discrete polynomial-phase transform)和ACCF(adjacent cross correlation function)思想的高机动目标检测方法,但该类方法对输入信噪比要求较高。
文中从运算量减小和弱目标检测性能提高两方面折中考虑,重点分析了第二类方法对弱信号检测能力降低的原因,从提高运算效率和检测性能的角度出发,提出一种基于互相关和FRFT结合的相参积累算法,通过分析脉压信号的频域结构,利用互相关方法实现回波信号中速度与积累时间的解耦;接着利用FRFT以及连续两帧回波信号的距离信息,获得目标的相关运动参数,并仿真对比分析了所提方法检测性能改善。
1 目标回波信号模型
假设雷达发射的第n个脉冲信号为[14]:
(1)
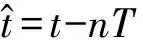
由式(1)可得第n个脉冲回波信号为:
(2)

忽略噪声的影响,则由式(1)和式(2)可得第n个回波信号脉压处理后的频域表达式为:
(3)
式中:初始时延τ0=2R0/c;时延变化率β0=2v0/c;多普勒频率一次变化率fd=2v0/λ;加速度αd=2a/λ;波长λ=c/fc;fc为载波频率。
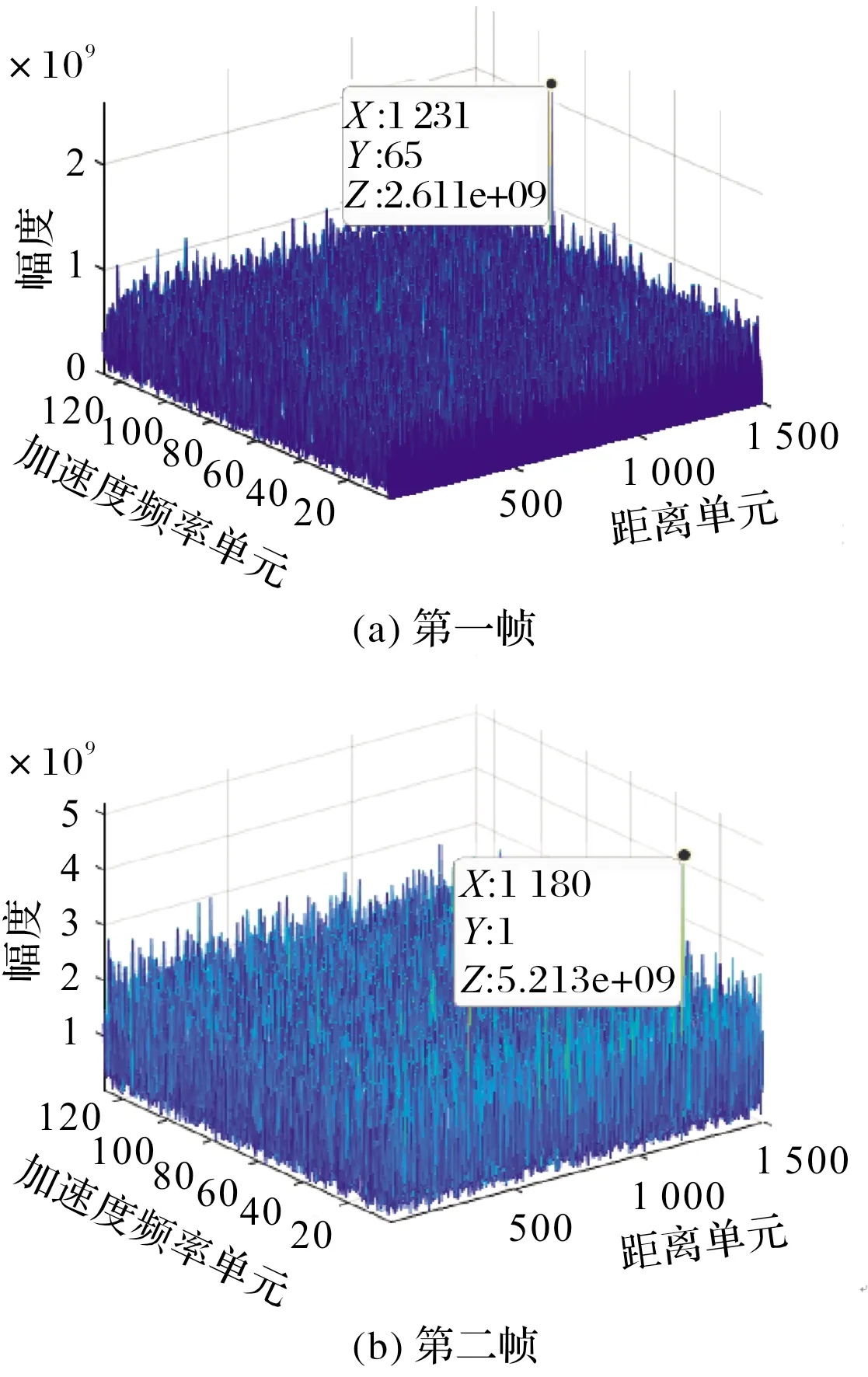
一般情况下fd< (4) 式中:时宽带宽积D=BT0,B为信号带宽,T0为信号脉宽长度。 对式(4)进行MTD处理后可近似表示为: (5) 从式(5)可以看出,目标速度和加速度越大,回波积累能量扩散现象越严重,目标检测概率越低,虚警概率越高。为了实现目标能量的有效积累,从回波脉压信号的频域出发,提出一种互相关处理和FRFT算法结合的高机动目标检测算法。 考虑速度和加速度对脉压回波信号频域的影响,将式(3)的频域形式重写为: (6) 将式(6)进行互相关处理,可得: (7) 由于N>>1,则式(7)可变为: (8) φ=2παd(n2-nN)T2 (9) f=-αdNT+2αd(nT) (10) 由式(10)可知,加速度引起的目标回波近似调频率为2αd的线性调频信号(LFM),为了消除其关于FFT频谱的扩散现象,引入FRFT对其进行处理,其δu阶分数阶傅里叶变换可表示为[8]: (11) 当阶次p与调频率估计值k′=2αd匹配时会形成一个峰值,由峰值对应的参数即可获得信号的初始频率和调频率,即: (12) (13) 由式(10)、式(13)可得目标的加速度估计值为: (14) 将式(8)按行关于f进行IFFT处理后,再关于n进行FRFT处理,可得: (15) 对式(15)进行最大值搜索,可获得目标对应的时延和加速度信息。 另外,本算法中的速度信息可通过连续两帧目标信号的位置进行估计,即: (16) 表1 不同算法复乘量 设雷达工作载频为3 GHz,脉冲重复周期为3 ms,积累脉冲数为128,信号带宽为5 MHz,基带采样率为10 MHz,目标为点目标,其径向速度最大为800 m/s,径向加速度最大为5 m/s2, 输入信号信噪比为-20 dB。对比图1、图2可得:文中算法和文献[14]算法都能很好的对高机动目标进行检测,而MTD算法会出现频谱能量扩散现象。图2(b)、图2(c)分别给出了经过式(7)、式(11)处理后,加速度对目标回波的影响。从图2(b)中可以看出,回波频谱近似为LFM信号的频谱;图2(c)为经过FRFT处理后的结果(阶次为1.14),对应的加速度为4.97 m/s2,与所设的理论值基本一致。 图1 MTD与文献[14]处理 图2 文中算法处理 为进一步验证文中算法的优势,设其径向速度最大为1 200 m/s,径向加速度最大为10 m/s2, 输入信号信噪比为-25 dB。图3为MTD与文献[14]处理结果,图4为连续两帧信号的处理结果。对比图3、图4可知,文中算法在低信噪比下,检测性能好于其它方法。同时,根据连续两帧信号(第二帧信号取自于第一帧信号后续的128个脉冲)获得的距离信息,可计算目标速度为1 192 m/s,计算值与理论值基本一致,验证了算法的正确性。 图3 MTD与文献[14]处理 图4 文中算法连续两帧处理结果 为了分析文中算法的多目标检测性能,设雷达探测目标有2个,其中目标1的径向速度最大为1 200 m/s,径向加速度最大为10 m/s2, 目标2的径向速度最大为500 m/s,径向加速度最大为10 m/s2,输入信号信噪比为-20 dB。图5(a)给出了MTD处理结果,图5(b)为文献[14]处理结果,图5(c)为文中算法处理结果,从中可以看出,MTD方法无法对两目标进行分辨,文献[14]方法对两目标分辨不明显,而文中算法处理后,两目标分辨明显,验证了所提算法对多目标检测的优势。 图5 文中算法多目标检测性能 针对高机动目标雷达探测的难点,提出通过对回波脉压信号的频域形式进行互相关处理,可消除速度对回波包络走动的影响,进而通过FRFT方法消除加速度对回波频谱扩散的影响,并获得目标时延、距离、速度、加速度等信息;理论和仿真结果表明,该算法复杂度和检测性能较其它方法具有较好的折中性能,对工程化应用具有较好的参考价值。

2 基于互相关处理和FRFT的目标检测算法
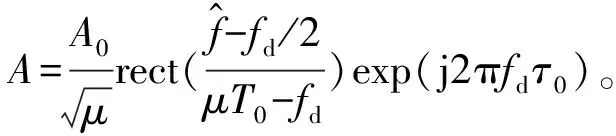
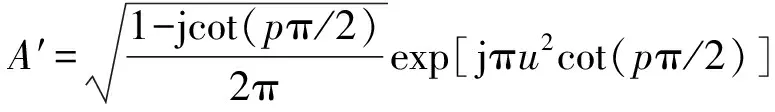

3 算法复杂度对比分析

4 算法检测性能分析
4.1 单目标检测性能分析



4.2 多目标检测性能分析

5 结论
