含Z 向钢针阵列立体织物钢针置换摩擦力分布规律
2022-01-09董九志陈云军蒋秀明
董九志,季 绅,陈云军,蒋秀明
(1.天津工业大学天津市现代机电装备技术重点实验室,天津 300387;2.天津工业大学电气工程与自动化学院,天津 300387)
整体穿刺成型工艺是指先将机织布依次按0°和90°(经向和纬向)的方向层叠铺放在钢针阵列上,通过穿刺模板的加压密实至一定厚度之后再用纤维取代穿刺钢针形成一种立体织物的编织技术[1]。该工艺制得的三向正交立体织物常被用于碳/碳(C/C)复合材料的预制体[2-3],织物中铺层叠放的碳布在经过穿刺加压密实之后,大大增强了对Z 向的摩擦作用,当用碳纤维束或碳纤维棒置换掉Z 向钢针后,层叠碳布与Z 向碳纤维束整体捆绑。因此,整体穿刺织物不仅在X-Y向交织连接,且Z 向与X-Y 向之间也存在高度摩擦捆绑,这样不仅大大增强了立体织物整体的稳固性,同时也增强了织物的体积密度,可达0.7~0.9 g/cm3[4]。
C/C 复合材料因其具有良好的耐烧蚀性能、高抗拉强度和高拉伸模量,多被应用于导弹端头帽、固体火箭发动机喷管和其他航空航天领域重要结构的制造[5-7]。国内外研究热点多集中在以整体穿刺预制体复合成型的C/C 复合材料的力学、热力学性能[8-10],但对其预制体置换工艺研究报道较少。在实际钢针置换过程中,织物中不同位置处的钢针置换摩擦力往往不同。为此,本文建立了织物力学模型,研究了整体穿刺织物钢针阵列分布规律,可以为今后置换阻力的预测以及钢针置换装置的合理设计提供理论参考。
1 钢针置换摩擦力成因分析
正交层叠碳布在经过整体穿刺、加压密实工艺后制得了含Z 向钢针的立体织物,但要最后制得整体穿刺织物需用碳纤维纱线或碳纤维棒逐根置换掉织物中的穿刺钢针,钢针置换工艺如图1 所示。在进行钢针置换工作时,保留了立体织物上下两块穿刺模板,用以束缚穿刺钢针两端,使其在钢针置换工艺过程中起到导向作用。为使碳纤维束或碳棒能顺利置换出织物内的穿刺钢针,就需要克服钢针与立体织物中正交层叠碳布之间的摩擦,即钢针置换摩擦力。
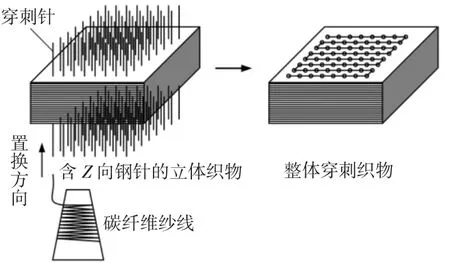
图1 钢针置换工艺Fig.1 Steel needle replacement process
钢针置换摩擦力的成因为立体织物中层叠碳布对穿刺钢针针杆施加的横向作用力,可分为2 种形式:①纤维束绕针张力对钢针的作用;②相邻钢针间纤维束对钢针的挤压作用。
第①种,碳布面内纤维束出现绕针现象[11-12]。纤维束绕针有2 种形式,如图2 所示。图2(a)所示为在理想状态下,整体穿刺之后织物中纤维束应均匀地在钢针间隙间直穿;但在实际情况下碳布在与Z 向钢针阵列整体穿刺后,一部分纤维没有挤占理想的钢针阵列的间隙,这些纤维束发生复杂的弯曲和伸长现象(如图2(b)所示),并对钢针径向施加作用力,产生了一个静摩擦fp。若设μ 为碳纤维束与钢针间的摩擦因数,则此摩擦力大小为fp=μP[13]。实际上,在穿刺层数较多的情况下,这种工况产生的摩擦力的值较实际置换阻力的值小很多;又由于发生纤维束绕针情况的随机性、纤维绕针形式的随机性和绕针纤维束中纤维含量的随机性,均导致了fp值的不确定性,研究难度较大。因此,纤维束绕针现象对钢针的作用可视为形成钢针置换摩擦力的次要因素。

图2 纤维束绕针形式Fig.2 Methods of fiber bundle winding needle
第②种,钢针间隙中受挤压的纤维束产生对钢针的反作用力。穿刺完成后,钢针阵列挤占了碳布布面面积,大量碳纤维被挤压在钢针阵列的间隙中,钢针间纤维束受挤压产生对钢针的弹性反作用力,从而形成置换阻力Ff。当钢针阵列密度越大,穿刺层数越多时,由第②种因素产生的置换阻力越大,因此该因素通常视为置换阻力形成的主要因素。本文将就此类置换阻力成因进行分析研究。
2 纤维束的横向压缩性能
立体织物中相邻钢针间纤维束的挤压作用是产生钢针置换摩擦力主要原因,在研究纤维束整体变形行为时可按照多数纺织研究工作人员的建议,将平行单一取向的纤维束处理为横观各向同性的连续体,如图3 所示。

图3 平行排列纤维束的典型单元Fig.3 Typical unit of parallel arrangement of fiber bundles
纤维束受横向挤压的纵向变形机理近似视作满足一般材料的泊松效应,但由于纤维束纵向变形对钢针摩擦力的大小几乎没有影响,因此在本文研究中忽略纤维束受压时纵向变形情况仅考虑受压方向的变形情况即横向变形情况。
朱建勋等[13]提出了一个织物压缩变形的理论模型,即把织物视作是纱线或纤维与空气的集合体,得出了研究织物在受压缩过程中压力与受压方向形变量的关系,并通过实验验证了此模型的合理性,根据横向压力与横向形变关系图,纤维束压缩形式可分为3 个阶段[14-15],如图4 所示。

图4 织物压缩性能Fig.4 Compression performance of fabric
第1 阶段:测试盘接触到纤维束表面突起的纤维,压缩阻力主要来自于这些突出纤维的弯曲。对于纤维束来说,测试盘的压力施加在纤维束边缘处的纤维,此时纤维集合体内的空隙较大,纤维堆砌密度不高,纤维间作用力很小。
第2 阶段:测试盘与纤维束表面接触,并将纤维束内纤维压缩至一般挤紧状态。此时,纤维堆砌方式重组,纤维堆砌密度增大,纱线间和(或)纤维间的摩擦产生抗压阻力,直至所有纤维相互接触。
第3 阶段:施加在纤维束上的压力继续增大,纤维紧密堆砌,纤维间的空隙已经很小,因此,抗压阻力来源于纤维自身的横向压缩。
纤维束压缩的第1 和第3 阶段主要是弹性变形,其压缩曲线可近似拟合为线性方程y=a+bx;第2 阶段的压缩曲线可以回归为指数方程y=abx+c,摩擦力占主导作用。其中:y 为压缩压力(N/cm2);x 为纤维束压缩变形量(mm);a 和b 均为回归常数[16]。在整体穿刺织物中,穿刺钢针对碳纤维挤压作用明显,钢针间隙中纤维束堆砌密度高,因此纤维束压缩的第3 阶段适用于描述立体织物内的纤维集合体的压缩状态,即钢针间受压缩的碳纤维束可以近似视作受压缩的线性弹簧[16-17]。
3 立体织物力学模型建模
3.1 织物组织的质量弹簧模型
含Z 向钢针的立体织物可分为4 个结构完全一样的部分,这4 部分织物力学情况可视作完全一致,如图5 所示。取其中区域Ⅰ进行研究,由于织物中钢针受到来自于经向纤维束与纬向纤维束压缩反力的共同作用,且2 种压缩反力成因一致,可将钢针受力正交分解,并取该区域中任意行的织物组织进行分析,即分析钢针在仅受经向纤维束作用的情况。将纤维束简化为弹簧刚度的线性弹簧后待置换的穿刺织物力学模型如图6 所示。
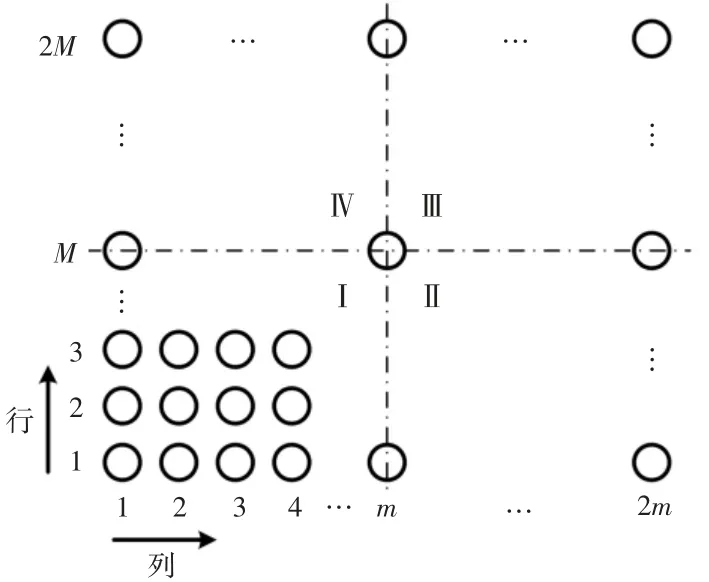
图5 织物组织的分区Fig.5 Division of fabric structure

图6 单行(列)织物组织力学模型Fig.6 Mechanical model of single row(column)fabric structure
图6 中,从该织物组织中截取任意第z 层的织物组织分析,该层织物组织中任意钢针微段的受力情况如图7 所示。

图7 钢针微段受力分析Fig.7 Force analysis of steel needle micro-section
图7 中,钢针微段上存在的主要作用力为:①钢针两侧纤维束弹性体产生的合抗压阻力q(z);②纤维束层间摩擦力和绕针弯曲产生的张力对钢针的作用力,这两种力阻碍了织物内钢针发生弯曲变形,且较难预测,可计为合阻力f′;③钢针微段上下表面存在因钢针弯曲引起的剪力Fs和Fs+ΔFs,弯矩M 和M+ΔM,其中ΔFs和ΔM 为剪力和弯矩增量。由钢针微段的力平衡方程∑F=0 得:

对该层织物组织分析,研究受力后各钢针微段产生的偏移情况。考虑到织物组织中间处的钢针左右两侧受到力的大小几乎相等,合力几乎为零,可假设织物中间处钢针m 未发生弯曲变形,即第m 根钢针视作固定的墙体。将织物组织简化为多个质量和弹簧组成的离散线性系统,如图8 所示,记F=ΔFs(z)+f′(z),视作作用在钢针微段上同时造成纤维束压缩的外力。

图8 单层织物组织质量弹簧离散线性模型Fig.8 Discrete linear mass-spring model of single-layer fabric structure
3.2 织物模型柔度影响系数
根据机械振动学理论可知,一个系统的柔度影响系数或刚度影响系数可以用来描述作用在该系统上的力与因此产生的位移之间的关系[18]。对于本文建立的质量弹簧的织物模型来说,可以以此推断出模型中纤维束受压缩情况和钢针弯曲变形情况。
由于该系统存在m-1 个自由度,则该系统共有m-1 个广义坐标,并对应着m-1 个位移,所以该系统柔度矩阵A 由(m-1)×(m-1)个柔度系数ast组成:

式中:柔度系数ast的定义为由施加在第t 个质量块上的单位力Ft= 1 所引起的第s 个质量块发生的位移量。根据系统柔度影响系数的定义,依次分别令外力Fm-1,Fm-2,…,F1为单位力1,同时令其他外力为0,即可求出系统中各柔度系数,将这些柔度系数组合成系统的柔度矩阵,柔度系数计算如图9 所示。
令Fm-1=1,F1=F2=…=Fm-3=Fm-2=0,如图9(a)所示,质量块m-1 产生的位移为:

由于除质量块m-1 其他质量块不受力,因此其他质量块产生的位移与质量块m-1 相同,即:
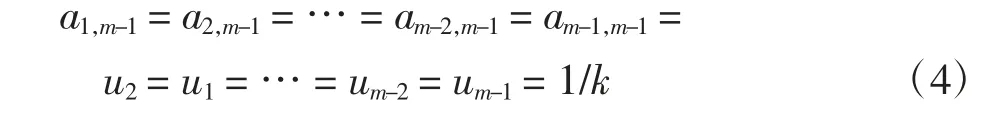
令Fm-2=1,F1=F2=…=Fm-3=Fm-2=0 如图9(b)所示,质量块m-2 受到两个弹簧km-1和km-2的串联作用,则质量块m-2 的位移为:
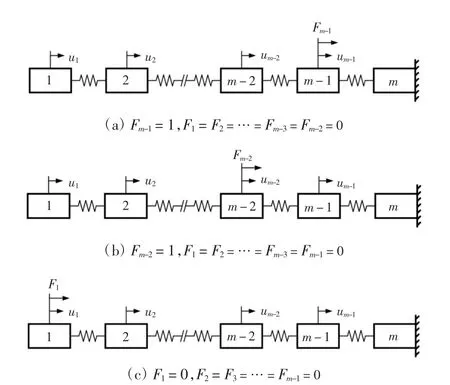
图9 柔度系数的计算Fig.9 Calculation of flexibility coefficient

质量块1,2,…,m-3 的位移与质量块m-2 相同,即:

3.3 钢针阵列置换摩擦力分布规律
在上述系统模型中,合力Fj=ΔFsj(z)+fj′(z)是施加在该系统中的外作用力,写成矩阵形式为:

求得:

可以看出,系统模型中各质量块产生位移量的关系为u1>u2>…>um-1,外侧的质量单元发生的位移大于内侧质量单元产生的位移。实际当中,穿刺织物钢针置换摩擦力的大小根本上取决钢针相邻纤维束弹性体压缩量的多寡,即模型中质量块间弹簧压缩量多寡。各弹簧的变形量Δlj(j=1,2,…,m-1),可由相邻两质量块位移量作差求得,则各弹簧的变形量为:

容易得到,Δl1<Δl2<…<Δlm-1,即纤维弹性体受压变形量由织物外侧向内侧逐渐增加,即织物内部的挤紧程度更高。容易推之,织物内侧的纤维束产生的挤紧压力高于外侧纤维束产生的挤紧压力,进而推之,钢针置换摩擦力由织物外部向内部逐渐增大。
4 实验设计及实验结果分析
实验采用的含Z 向钢针的立体织物的外形尺寸为110 mm×110 mm×67 mm,层密度为20 层/cm。穿刺钢针阵列为46 根×46 根的四方点阵,穿刺钢针为直径1.2 mm 的不锈钢钢针,钢针间距为2.3 mm,穿刺碳布采用3 K 的T300 纤维束织造得到,平均厚度为0.25 mm。
钢针置换摩擦力采用型号为艾普SF-300N 高精度数显拉力推力计进行测量,该测力计测量精度为±5%,并且具备工作跟踪和峰值保持功能,可确保实验数据有效性。
实验时,在穿刺织物区域Ⅰ中选取间隔均匀的钢针作为实验对象(相邻测量点之间间隔3 行(列)),共选取36 个实验对象,用专用测力端头顶住待测钢针的一端,用测力计推动待测钢针并读取测量数值。根据实验数据绘制的散点图,如图10 所示。由图10 可以发现,立体织物中钢针置换摩擦力从边缘区域向核心区域逐渐增大,此结论与理论预测结果一致。

图10 实验数据散点图Fig.10 Scatter plot of experimental data
立体织物中各处纤维的挤紧程度主要由钢针阵列偏移情况体现,为研究整体穿刺织物内外侧处纤维挤紧程度的差异,参考文献[19],可通过以下实验探究。
(1)将穿刺模板拆除,使钢针发生自由偏移,在织物中选取间隔均匀的且与织物中性线对称的行(列)向钢针阵列范围,测量各实验对象行向、列向两端钢针的距离W 或W′,如图11 所示,测量得到的实验数据如表1 所示。
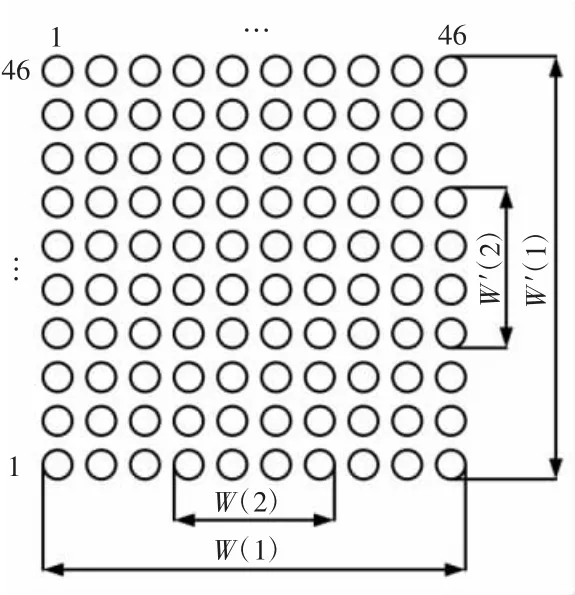
图11 实验分组方法Fig.11 Method of experimental grouping
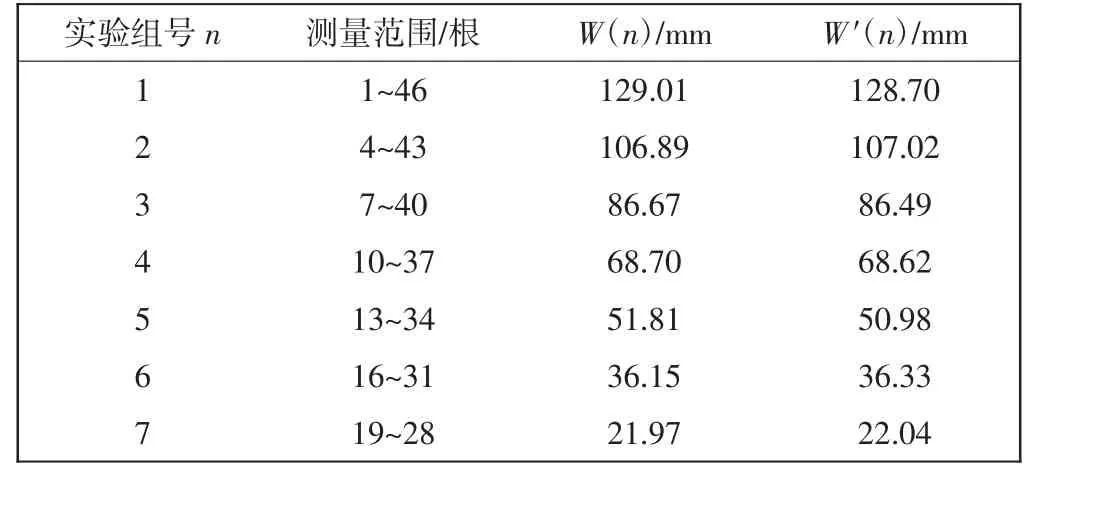
表1 实验数据Tab.1 Experimental data
(2)接着将实验数据W 和W′通过式(14)和式(15)处理,得到织物不同层内钢针的平均间距p 或p′,具体结果如图12 所示。若p 或p′值越大说明该层织物内的钢针整体偏移越大,纤维挤紧程度则越小,反之,纤维挤紧程度则越大。

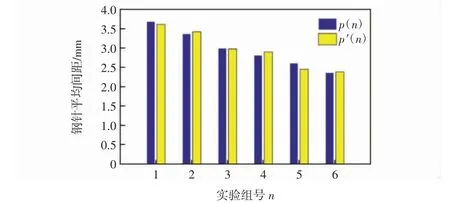
图12 织物各层行(列)向平均钢针间距Fig.12 Average steel needle spacing in row(colum)direction of each layer of fabric
由图12 可知,外侧行(列)钢针阵列的偏移量较内侧更大,说明织物内侧纤维与钢针的挤紧情况比外侧更大,这与理论预测情况一致。同时结合上一个实验结果,证明了纤维与钢针挤紧情况的差异是导致钢针置换摩擦力大小差异的主要因素。
5 结 论
(1)分析了含Z 向钢针立体织物钢针置换摩擦力产生的主要原因是钢针间隙间纤维束受压变形产生的挤紧压力。
(2)对立体织物进行细观分析,建立了单行单层织物组织的质量弹簧模型,发现纤维挤紧程度由织物外层向内层逐渐增大,导致了钢针置换摩擦力从外侧向内侧逐渐增大的现象。
(3)通过实验结果分析发现,实际钢针阵列偏移情况与钢针阵列置换阻力分布情况与本文理论预测结果一致,证明了本文建立的模型合理性。
