基于总变差正则化算法的三维肺部呼吸过程电阻抗成像方法

王 琦，陆纪璇，李秀艳，段晓杰

（1.天津工业大学生命科学学院，天津 300387；2.天津工业大学天津市光电检测技术与系统重点实验室，天津300387；3.天津工业大学电子与信息工程学院，天津 300387）

电阻抗断层成像技术（electrical impedance tomography，EIT）是一种通过电极给予人体微弱的电流激励，以此测量人体表面电压来计算人体电阻抗分布的技术，具有实时、安全、便携的优点，并对电导率变化的捕捉十分敏感。由于肺部充满空气，肺部内区域与周围组织之间的电导率差异较大，且肺部容量不断变化，导致其电导率分布处于持续变化的状态，因此，EIT 成像技术非常适用于肺部成像[1-2]，可用于肺功能的连续监测。现已证明EIT 在肺部功能测试中有显著效果，在保护肺部通气过程中能够进行可视化实时反馈[3-4]，在治疗慢性阻塞性肺病（chronic obstructive pulmonary disease，COPD）[5]、哮喘[6]、囊性纤维化[7]、气胸[8]和肺水肿[9]等方面使用EIT 成像已经取得很大进展[10-12]，目前已有临床EIT 产品问世。使用EIT 技术能够对肺部疾病进行安全有效的指导[13]，不仅对成人患者有效，对新生儿和幼儿患者均有益处。由于人体的三维特性，传统的二维EIT 成像方法观察范围有限，不能很好地满足诊断、监测需要，因此，实现三维成像是EIT 技术发展的趋势。

总变差（total variation，简称TV）正则化算法采用总变差函数作为约束项，可以有效克服Tikhonov 正则化算法导致的过度平滑问题，并具有运行速度快、保边性好等优点。因此，TV 算法对于肺部三维图像重建是一个很好的选择。

本文利用EIT 重建技术对肺部呼吸运动进行监测。首先，基于CT 切片构建人体三维胸腔模型，即呼气末模型和吸气末模型，进行仿真研究；其次，采用TV 算法与Tikhonov 正则化算法对肺部仿真数据与实验数据进行三维图像重建，并对2 种算法的图像重建结果进行对比与评价。

1 EIT 重建基础

EIT 通常采用差分成像方法，将感应域电导率相对于参考电导率图像的变化与测量的边界电压差V的关系表示为：

式中：F 为非线性正演算子；e 为测量噪声。在实际情况下，式（1）可线性化，表示为[14]：

式中：V 为归一化电压测量；J 为雅可比矩阵或灵敏度矩阵；σ 为物场与空场之间的电导率变化向量。

EIT 技术包含正问题与逆问题。正问题求解过程为通过“原因”求“结果”，此过程一般是常态的、适定的，具有唯一且稳定的解。逆问题求解过程即图像重建过程，由边界电极测得的边界电压联合正问题中求得的灵敏度矩阵，反向推导被测区域内的电导率分布。逆问题求解过程即为由“结果”推“原因”，因此，该过程是病态的、不适定的，它的解不是唯一存在且稳定的，微小的变化都会引起解的极大变化。

由于电导率分布的变化对最终边界电压测量值的变化影响较小，导致逆问题的求解计算过程变得十分不稳定。对于边界电压测量值，微小的改变便会对最终解产生巨大影响，导致计算求得的电导率分布与实际电导率分布可能会相差甚远[15]，这是EIT 逆问题求解过程中面临的最大难点。

2 基于EIT 正问题的人体三维胸腔模型构建

本文基于CT 扫描图片，提取人体真实胸部轮廓与肺部轮廓，进行组合之后形成模型。三维胸腔模型的构建过程如图1 所示，基于最大类间方差算法[16]，首先提取出胸腔和肺部轮廓并进行叠加，得到模拟胸腔的初步模型；然后利用SolidWorks 软件对三维模型进行平滑处理，使正演问题得到稳定求解；最后，在COMSOL Multiphysics 软件中将肺部、胸廓模型进行组合并安装电极，得到最终实验模型。

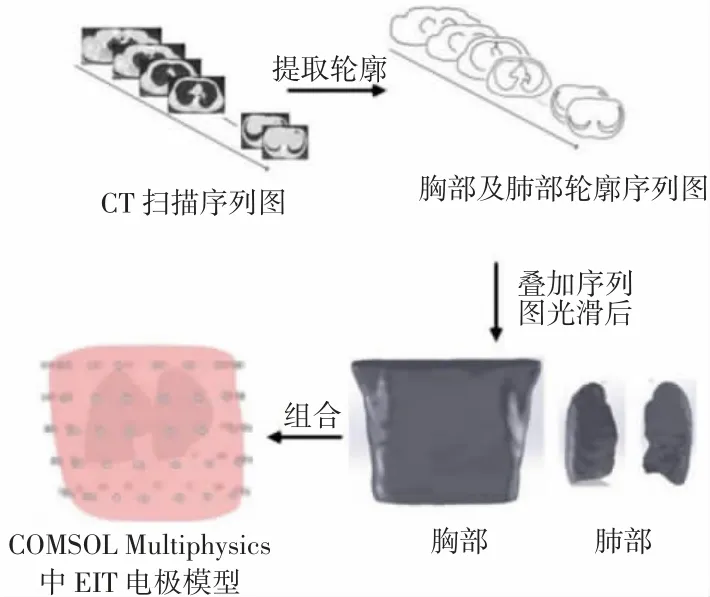
图1 建立人体三维胸腔模型的步骤Fig.1 Steps of establishing 3D thoracic model of human body

为了研究肺部EIT 的呼吸运动，本文在吸气末和呼气末2 种特定状态下建立了人体三维胸腔模型，对人体EIT 数据进行重构，如图2 所示。根据人体电导率特性[17]，将肺组织的电导率设置为σexp=120 mS/m来模拟呼气末端状态，胸腔电导率设置为σbkg=480 mS/m，吸气时会导致正常肺部区域的电导率变小，通过改变肺部电导率至σinsp=60 mS/m 来模拟吸气末端状态[17-18]。

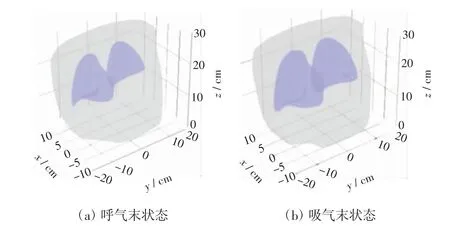
图2 2 种呼吸状态下的3D 胸腔模型Fig.2 3D thoracic models under two breathing states

通过对模型进行仿真实验，得到5 层电极测量值，对测量值进行图像重建，得到三维重建结果。由于内存限制和速度要求，将三维重建图像设为111 个重建层，即重建层间距为0.25 cm。建立三维逆问题网格，如图3 所示，图3 中所示的感知域纵向划分为111层，每层分辨率为32×32。

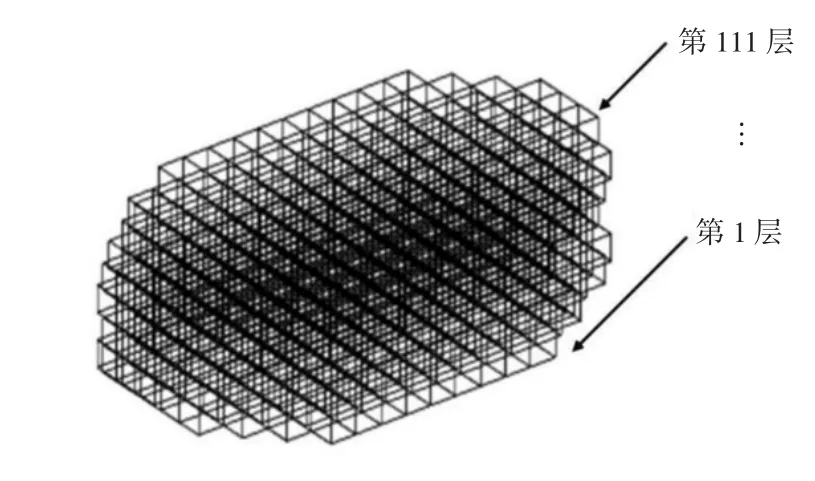
图3 用于逆问题计算的网格剖分Fig.3 Grid division for inverse problem calculation

根据电场的三维效应，通过获得单层电极平面的实测数据，可以得到重建平面图像。首先用单层电极环模型测试重建图像，如图4 所示，该模型电极层由16 个电极组成，每个电极直径为1 cm。采用相邻激励相邻测量模式，在3 kHz 的激励频率下注入10 mA 电流进行仿真，用COMSOL 软件求解三维模型的正问题。在测量中加入随机噪声，以此模拟测量当中可能出现的噪声。采用TV 算法和Tikhonov 正则化算法对每个平面上的图像进行单独重建。

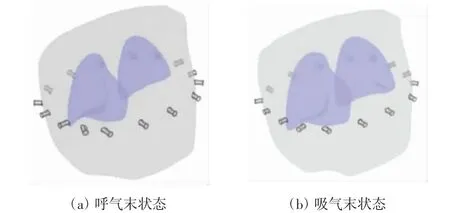
图4 一层EIT 电极的胸腔模型Fig.4 Thoracic models with a layer of EIT electrodes

本文选择相邻电极层间的20 个重构层，即每5 cm一层进行测量。因此，5 层电极环（每层电极环有16 个电极）可以覆盖整个胸腔区域的测量，如图5 所示，此种方式可以提高z 轴方向的轴向分辨率。

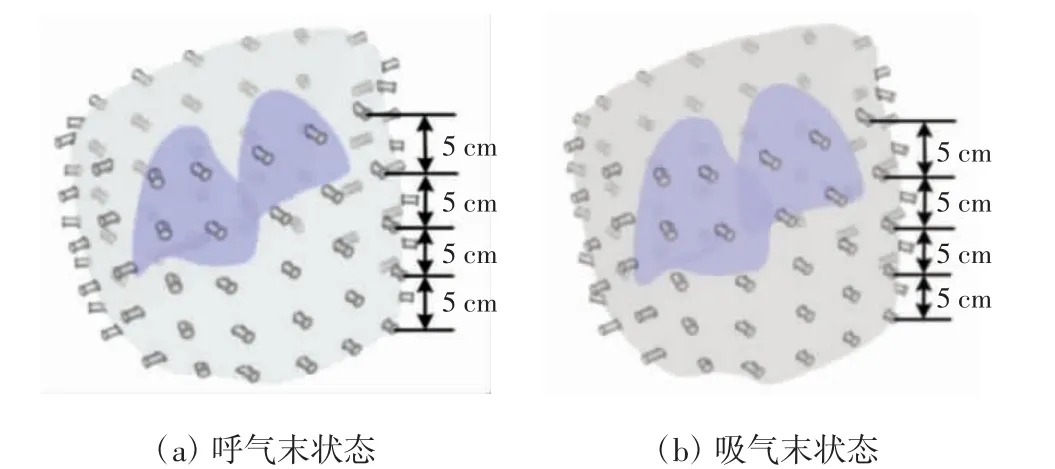
图5 5 层电极的3D 胸腔模型Fig.5 3D thoracic models with 5 layers of electrodes

3 Tikhonov 正则化算法和总变差正则化算法

3.1 Tikhonov 正则化算法

Tikhonov 正则化方法是常用的正则化方法，它可以求解很多在测量中出现的不适定问题，如拟合推估问题、病态问题等，通过选择合适的正则化参数，可以得到较好的结果。

Tikhonov 正则化方法的基本思想是将目标函数最小化：

经证明，STS+μI 的逆是存在的。因此，基于标准Tikhonov 正则化方法的解可以表示为：

正则化质量主要取决于正则化因子μ 的大小。μ值较小，能够对原始问题给出好的近似，但误差会影响解，使其不稳定；μ 值较大，会削弱解对误差的敏感性，但估计解一般会偏离真实值。因此，在实际应用中μ 值可以取中位数。理论上存在μ 的最优值，但由于其计算量过大，对于实时性要求较高的场合，选取μ 值主要还是依靠实际经验。

由于Tikhonov 正则化方法能够得到逆问题真实解的近似稳定解，并且重建速度较快，目前已被广泛应用。但由于此类方法采用2 范数形式的正则化函数（即（‖L（g-g）2‖））进行求解，即通过对重建图像进行一定程度的平滑后使重建过程趋于稳定，丧失了边缘信息，因此，图像的分辨能力不高[19]。

3.2 总变差正则化算法

由于Tikhonov 正则化算法得到的图像分辨率较差，Rudin 等[20]于1992 年首次提出一种基于总变差（total variation）正则化的图像重建算法，简称TV 算法。TV算法是一种应用于图像处理中的图像除噪技术，由于该方法在图像重建时具有较好的保边缘性[21]，因此，已经在图像处理领域得到广泛认可与应用。该算法能够提高逆问题解的稳定性，并能够提高非连续分布介质的区域成像分辨能力，具有良好的保边缘性，并且成像速度较快，可以满足EIT 系统对成像实时性的要求。

TV 算法在应用于EIT 图像重建时，采用归一化的介电常数σ 的总变差作为正则化函数，即：

式中：（xσ）、（yσ）和（zσ）分别为三维模型在x、y、z方向上的一阶局部差；指数i、j、k 为有限元网格中的单元。在传统的TV 算法求解中，通常引入平滑参数β[22]来近似原始TV 算法，使其在原点处可微。

4 图像重建

利用Tikhonov 正则化、TV 正则化方法对肺部EIT进行二维与三维图像重建工作，并根据重建结果对肺部呼吸运动进行分析。

4.1 二维重建

将仿真数据导入对应的Matlab 程序当中运行，通过不同算法对肺部进行二维分层图像重建，结果如图6 所示，左图部分为仿真模型和成像区域，右图部分为二维重建图像结果。

由于呼气末与吸气末的肺部状态不同，吸气末肺部状态充盈，呼气末肺部状态瘪小，因此，造成两种状态的有效肺部图像层数不一致，呼气末肺部状态有效图层为60 张，吸气末肺部状态有效图层为72 张。由图6 能够看出，Tikhonov 正则化算法和TV 算法均能在二维空间上反映肺部区域的变化。

图6 2 种算法重建二维肺部图像结果Fig.6 Reconstruction of two-dimensional images of lung with two kinds of algorithms

4.2 三维重建

4.2.1 评价参数

从理论上讲，重建图像可以反映不同呼吸状态下肺容积的变化。为有效评估2 种算法对重建图像的影响，评估不同方法构成的胸部模型与人体胸部真实结构的差异，本文采用肺部通气区域占胸部截面除肺部以外区域的比例即肺区域比（lung regional ratio，简写为LRR，用rLR表示）[23]及其误差对成像结果进行评价，其定义如式（10）所示：

式中：t（x，y）为像素点（x，y）的像素值；T 为肺部区域阻抗阈值，表示肺部区域最低阻抗值。那么SRV和SSV分别可由式（13）和式（14）表示：

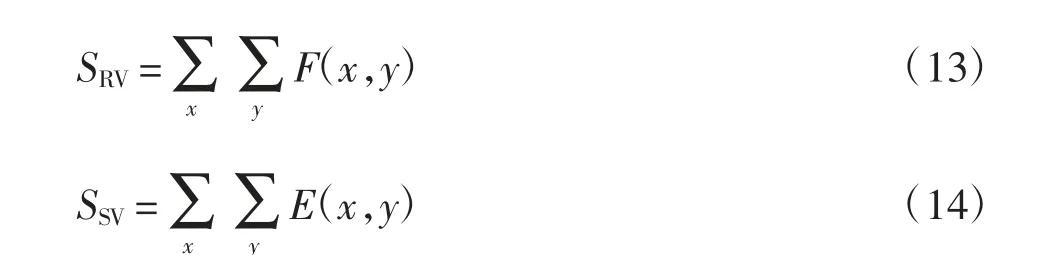
本文采用最大类间方差算法[24]确定区分肺部区域和非肺部区域的阈值。设f（x，y）为重建图像位置（x，y）处的灰度值，具有L 个灰度级（本文选取L 为20，即将归一化的电导率范围平均分为20 份），用变量b 表示灰度级。设灰度级bi的所有像素个数为fi，其中i=0，1，…，L-1，且b0＜b1＜…＜bL-1。重建图像像素数为N，则第bi级灰度出现的概率为：

式中：rLR1为基于仿真数据或实验数据的肺区域比；rLR0为基于真实数据的肺区域比。

4.2.2 基于仿真数据的三维图像重建

分别采用Tikhonov 正则化算法和TV 算法对肺部图像进行三维重建，如图7 所示。

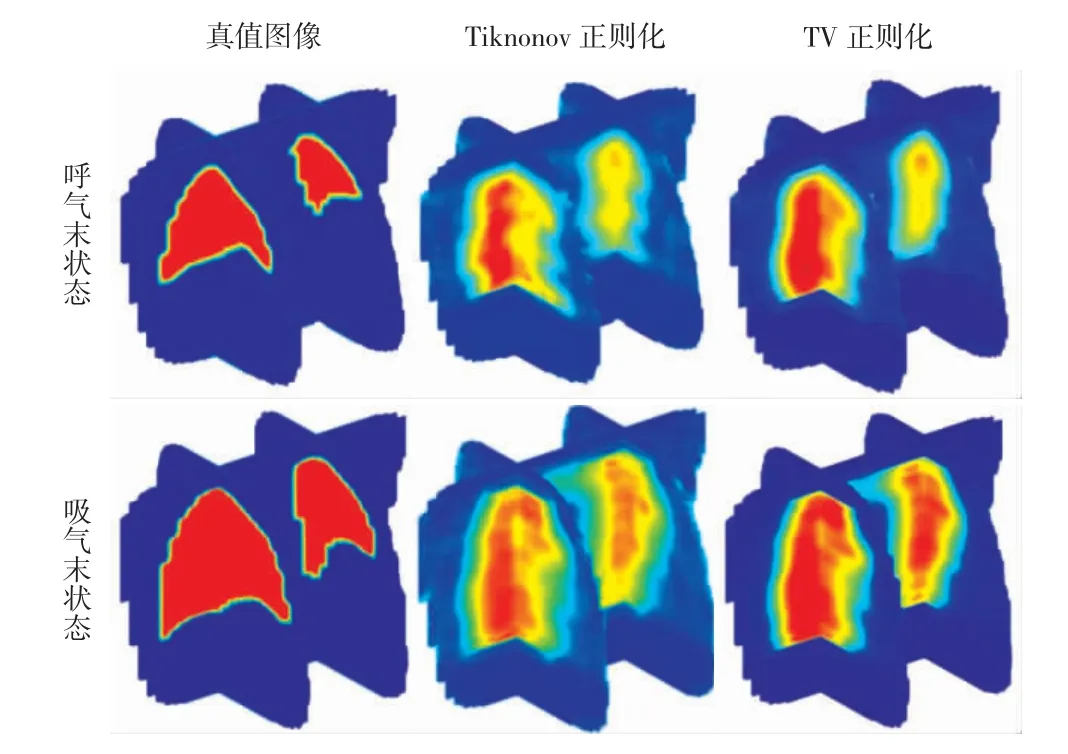
图7 基于模拟数据的肺部三维重建结果Fig.7 Three-dimensional lung reconstruction results based on simulated data

由图7 可以看出，2 种算法生成的三维重建结果在不同位置均具有一致性。对于不同的肺部情况，三维重建图像在肺叶位置和体积变化方面表现出的趋势一致。

Tikhonov 正则化算法能够生成一个平滑解，并且从图像上看可能会由于过于平滑造成图像边界模糊，与TV 方法相比，Tikhonov 正则化方法提高了反演结果的清晰度与表面光滑度，但由于过于平滑，并不适用于对被测物进行图像重建。

根据式（10）计算2 种呼吸状态下基于三维重建图像仿真数据的LRR 值，如表1 所示。在CT 扫描图像的基础上建立仿真模型，得到真实的LRR。

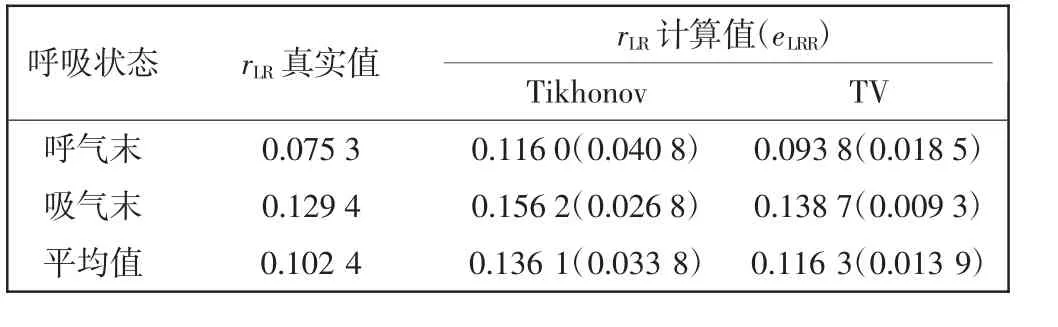
表1 基于仿真数据的LRR 比较Tab.1 Comparison of LRR based on simulation data

由表1 数据可以得出，基于仿真数据的图像重建结果中，与传统Tikhonov 正则化算法相比，TV 算法的eLRR降低了58.86%，LRR 值准确率提高了14.58%，更加接近真实值，不存在显著性差异。由此说明，TV 算法在降低成像误差方面有显著优势，能够使图像重建结果更精确。

4.2.3 基于实验数据的三维图像重建

通过提取人体CT 的胸腔以及肺部图像，利用3D打印技术，构建不同呼吸状态下胸腔、肺部的实验模型，采用光敏树脂材料得到透明的胸腔模型和白色的肺部模型，根据测算之后安装5 层电极。两种呼吸状态下的胸腔与肺部模型如图8 所示。

图8 3D 打印胸腔与肺部模型Fig.8 Models of chest and lung by 3D printing

肺部模型内部处于中空状态，通过导柱向其中填充质量浓度为9 g/L 的NaCl 溶液（即生理盐水）进行导电，以此模拟真实人体肺部。将激励频率设为50 kHz，激励电流设置为5 mA，采用相邻激励相邻测量的激励测量方法，通过TJPU-EIT 测量系统内的模块进行数据采集，得到相邻电极电压数据。测量过程如图9 所示.

图9 电压数据的测量过程Fig.9 Measuring process of voltage data

TJPU-EIT 系统为每层电极环提供一整套测量值Vj，k（j，k=1，…，16）。由于电流驱动电极上的电压容易产生误差，并受到其他未知接触阻抗的影响，因此，只能使用测量数据进行图像重建工作。与仿真数据实验相似，5 层电极覆盖了111 层胸腔切片。利用实验数据建立三维成像结果，如图10 所示。

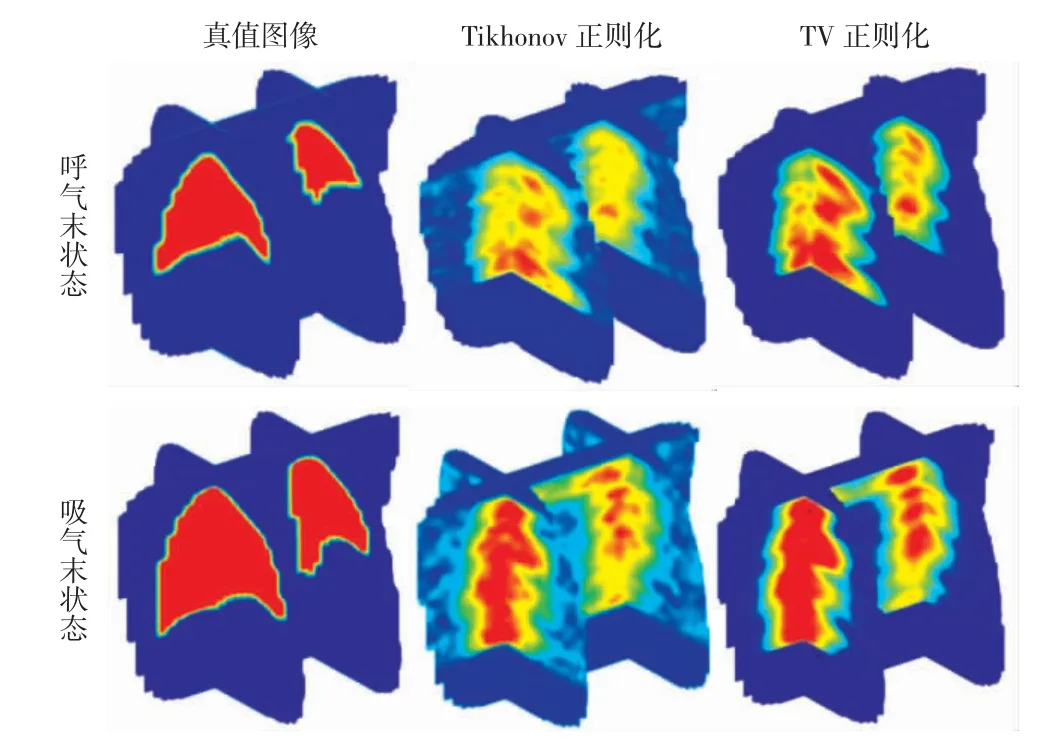
图10 基于实验数据的三维肺部成像结果Fig.10 Three-dimensional imaging results of lung based on experimental data

根据三维图像重建结果计算LRR 及其误差，结果如表2 所示。

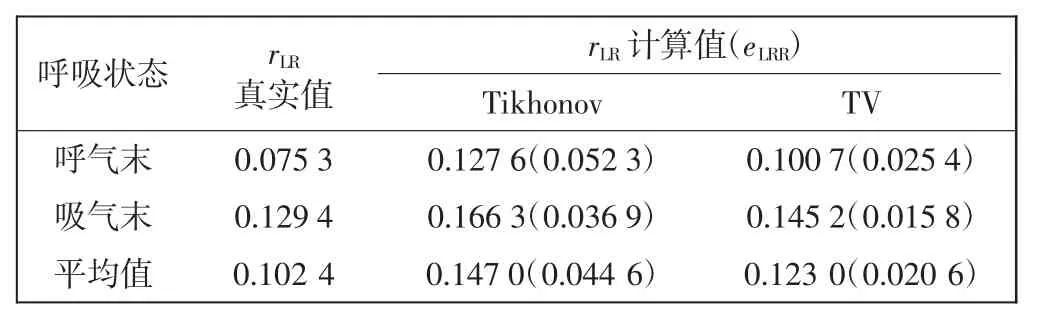
表2 实验数据的LRR 比较Tab.2 LRR comparison of experimental data

由表2 数据可以得出，基于实验数据的图像重建结果中，与传统Tikhonov 正则化算法相比，TV 算法的LRR 值准确率提高了16.33%，误差eLRR降低了53.81%更接近真实值，不存在显著性差异，说明TV 算法成像更精确，能够有效降低成像误差，提高成像效果。

5 结 论

本文利用三维肺部EIT 对呼吸运动进行研究，首先建立呼气末与吸气末状态的三维胸部模型，并根据非电极所在层的图像重建结果，讨论电极层间距的设计；其次，介绍了用于EIT 图像重建的Tikhonov 正则化算法和TV 算法，同时基于两种算法，对模型进行仿真成像与实验成像，并比较两种算法在图像重建结果上的优劣，结果表明：

（1）仿真数据中，与Tikhonov 正则化算法相比，TV算法使三维肺部EIT 成像误差降低了58.86%，肺区域比（LRR）准确率提高了14.58%；

（2）实验数据中，与Tikhonov 正则化算法相比，TV算法使三维肺部EIT 成像误差降低了53.81%，LRR准确率提高了16.33%；

（3）三维EIT 在肺部呼吸运动成像方面具有巨大潜力，TV 算法可以有效提高三维图像质量，从而提高肺部呼吸运动参数监测的准确性。