基于CDEGS建模的城市轨道交通杂散电流仿真与实验验证
2022-01-07李亚宁高晓红
李亚宁,李 猛,高晓红,王 烨
(1.兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2.兰州交通大学 环境与市政工程学院,甘肃 兰州 730070)
城市轨道交通具有容量大、缓解交通拥挤、快捷准时等优点,对于推动城市经济快速发展的重要性越来越显著[1]。牵引电流经钢轨(或走行轨)返回至牵引变电所负极的过程中,不可避免地产生杂散电流。该电流对埋地金属管线(如自来水管道、石油管道、天然气管道等)产生腐蚀、抬升轨-地电压、影响信号设备正常工作和危害检修人员安全等[2-5]。
通过钢轨泄漏至大地的杂散电流对列车安全运营的影响已引起国内外学者的高度关注,并产生了大量的研究成果。主要包括:提高轨-地过渡电阻的措施[6-7]、牵引变电所负极接地方式的选择[8]、绝缘垫电阻率大小[9]、牵引供电方式的选择[10-11]、牵引变电所的修建位置[12]、多层排流网对埋地金属腐蚀的影响[13-15]和牵引电压等级对杂散电流的影响等[12]。仿真模拟作为一种高效的研究方法,降低了对工程问题的研究成本。在CDEGS中,一般采用MALZ模块进行杂散电流仿真,且在仿真分析过程中,将钢轨置于地下,轨-地过渡电阻用给定的电阻率或者均匀涂层厚度进行近似的等效[16-18]。而在实际工程中,钢轨铺设在地面上,轨-地过渡电阻通常呈离散分布。仿真分析时的处理方式不符合工程实际,且目前尚未见电阻率与涂层厚度准确值的相关研究报道,因此,该仿真方法的应用受到一定程度的限制。基于工程实际,本文用CDEGS仿真软件建立仿真模型,将钢轨设置在地面上,使杂散电流仿真结果与工程实际更接近。
1 CDEGS仿真系统建模
机车、钢轨、轨-地绝缘和牵引变电所是直流牵引供电系统的基本要素,它们的参数设计和布置对杂散电流的实际分布会产生一定影响。本文研究对象为1 000 m长的轨道,采用单边供电系统,牵引电流大小为1 000 A。
1.1 走行轨和轨-地等效导体
为了计算和建模的方便,需要等效轨-地过渡电阻,其计算公式为
Re=Rg·N/L
( 1 )
式中:L为轨-地过渡电阻的等效长度,m ;N为等效导体的数量,个/km;Rg为轨-地过渡电阻,Ω·km;Re为轨-地等效电阻,Ω/m。
表1为采用CDEGS仿真时钢轨及轨-地过渡电阻模型相关参数的取值[19]。

表1 钢轨和轨-地过渡电阻模型参数
在SesCAD中建立如图1所示的钢轨及轨-地等效导体模型,两条纵向导体为钢轨(或走行轨),其长度为1 000 m,用轨-地等效导体来表示轨-地过渡电阻,各导体参数的取值及设定见表1。

图1 走行轨和轨-地等效导体模型
1.2 其他参数的设置
模型中除了钢轨外,还有埋地金属管线及排流网。在CDEGS仿真中,埋地金属管线及排流网的相关参数取值见表2[17]。在SesCAD中,排流网及钢轨在Y-Z方向的示意图如图2所示。
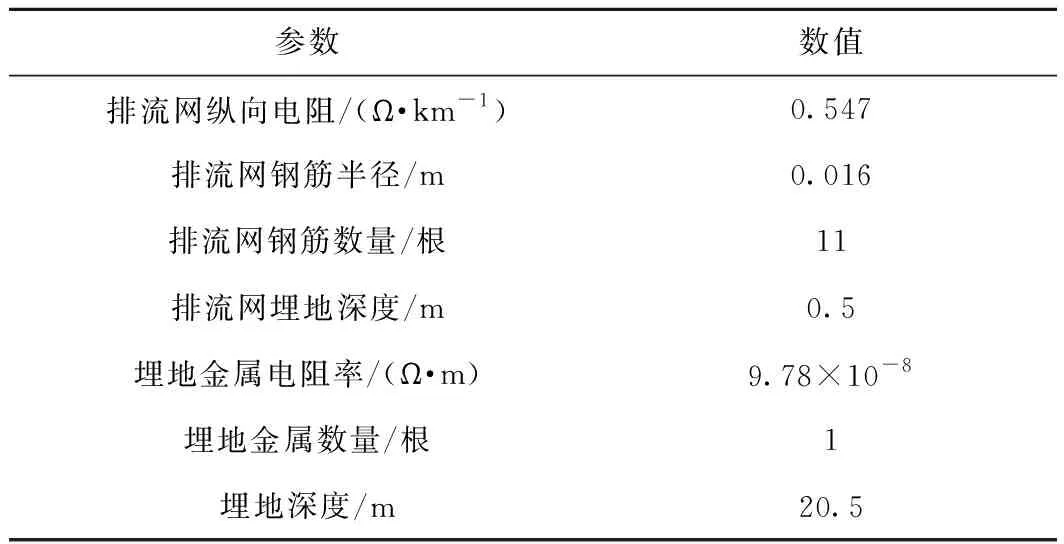
表2 排流网和埋地金属相关参数

图2 走行轨和排流网示意
1.3 土壤模型
在CDEGS软件中有很多内置土壤模型。本文建立两类土壤模型,即单层均匀土壤和双层土壤模型,共6种模型。模型A、B、C为单层均匀土壤模型,如图3所示,土壤电阻率取值为100、300、1 000 Ω·m;模型D、E、F为双层土壤模型,如图4所示。模型D上下两层的土壤电阻率取值分别为100、1 000 Ω·m,模型E取值分别为1 000、100 Ω·m,模型F取值分别为300、1 000 Ω·m。各模型中土壤电阻率取值参照文献[5]。
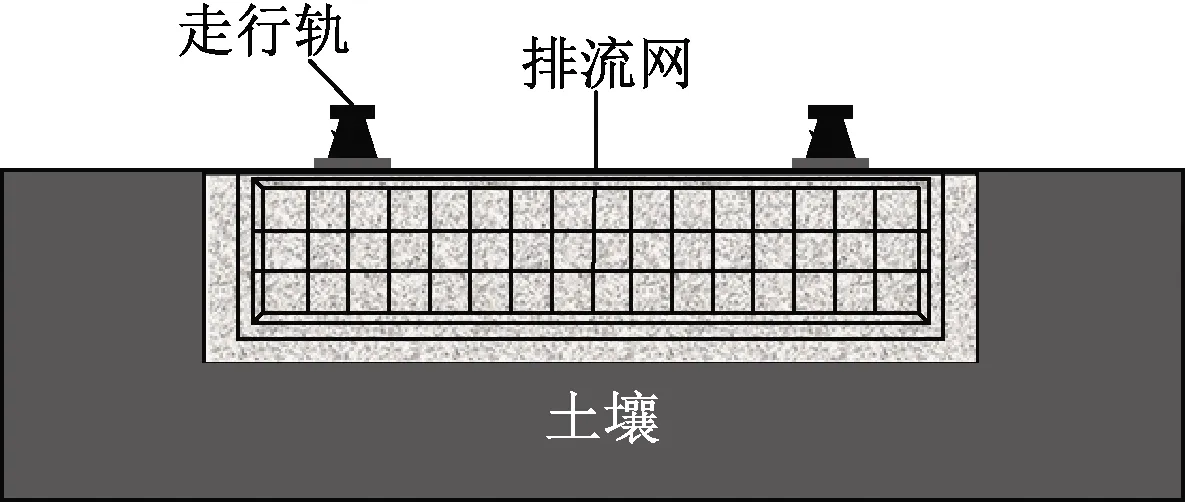
图3 单层均匀土壤模型
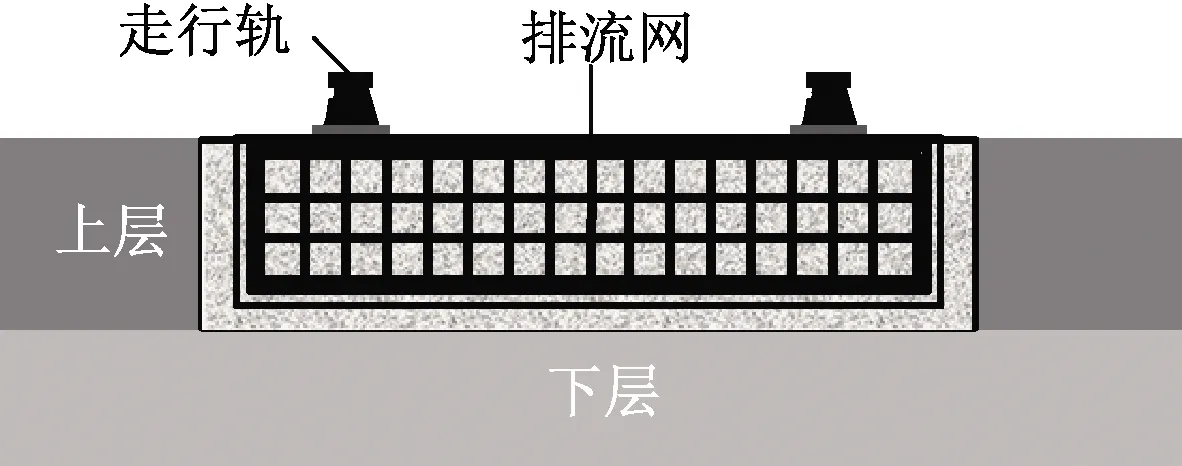
图4 双层土壤模型
2 仿真结果分析
2.1 均匀土壤模型
为了研究土壤结构对轨-地电压的影响,分别对模型A和模型B进行仿真,结果如图5所示。由图5可知,在模型A和模型B两种模型中,两条直线完全重合,说明轨-地电压几乎不受土壤结构的影响,其原因是轨道上的电压仅取决于钢轨纵向电阻。因此,当牵引电流为1 000 A、钢轨纵向电阻为20 mΩ/km时,机车端的轨-地电压为10 V,牵引变电所端的轨-地电压为-10 V,钢轨两端的总电压差为20 V,这一结论与文献[3]相一致。
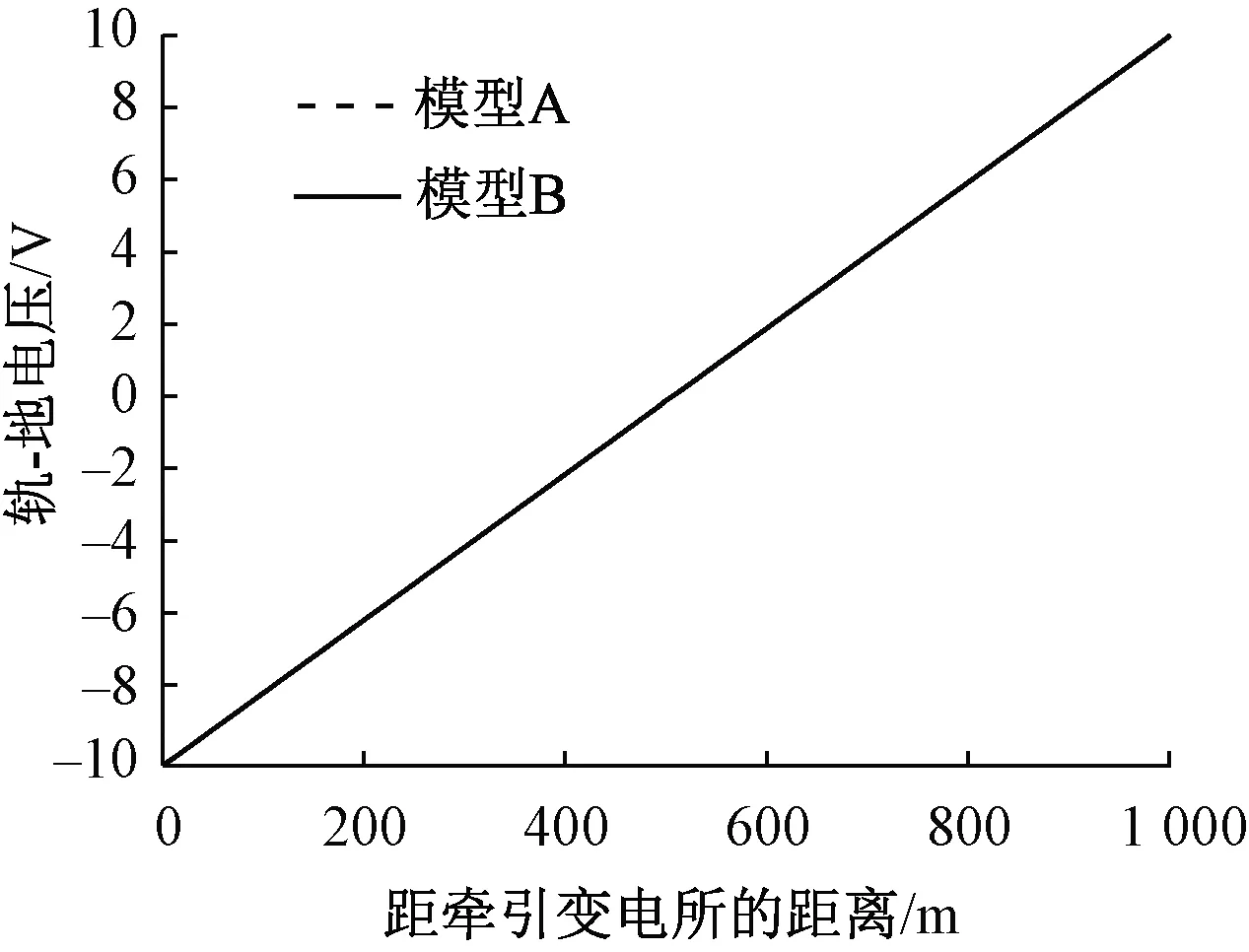
图5 土壤结构对轨-地电压的影响
即便轨-地电压不受土壤结构的影响,但土壤结构产生变化时,杂散电流在一定范围内的分布会受到影响。对模型A、B、C中机车和变电所距离在0~1 000 m范围内的杂散电流进行分析,杂散电流分布如图6所示。由图6可知,在0~500 m范围内,距牵引变电所距离增大,杂散电流也增大。而在500~1 000 m范围内,距牵引变电所距离增大,杂散电流反而减小;3种模型杂散电流的极大值分别为0.768 74、0.581 36、0.313 72 A。可见,在相同的变电所和机车距离情况下,杂散电流随电阻率增高而减小。
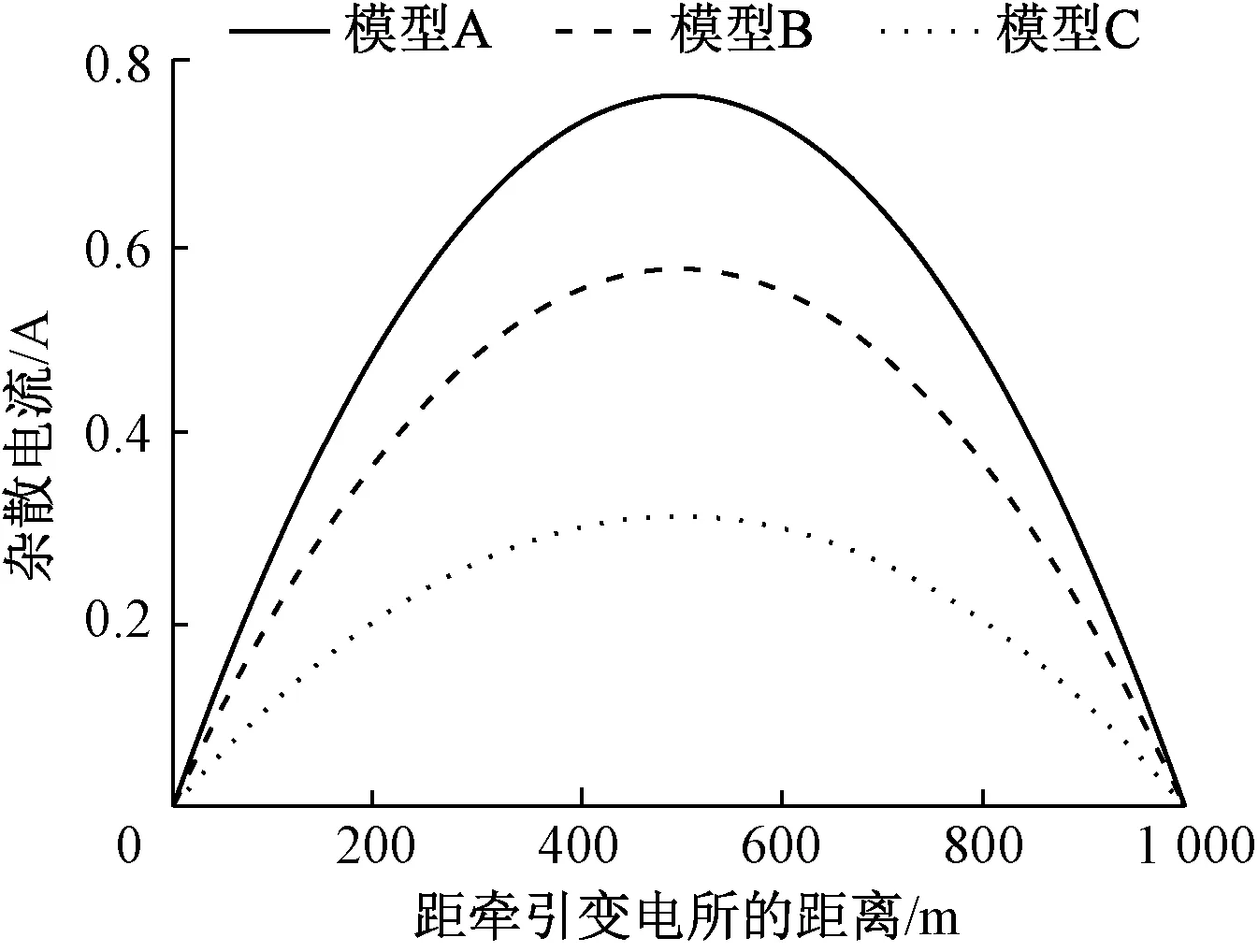
图6 均匀土壤模型中杂散电流分布
在均匀土壤(模型A、B、C)中,埋地金属与钢轨泄漏电流密度及变电所之间距离的关系如图7所示。由图7可知,在位置500 m处,埋地金属与钢轨泄露电流密度均为0;在0~1000 m范围内,变电所距离与钢轨泄漏电流密度之间的关系为正相关。
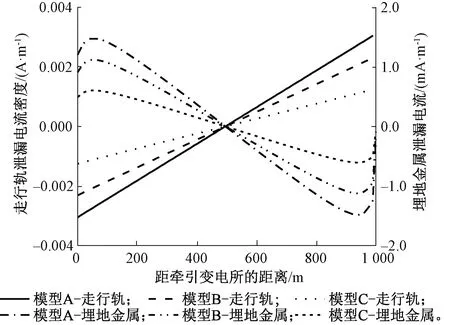
图7 走行轨和埋地金属泄漏电流密度变化曲线
在0~1000 m区间内,分为两个小区间:0~500 m区间和500~1000 m区间。前者杂散电流从大地流向钢轨,电流密度为负值,且距离牵引变电所越远,电流密度越小;后者杂散电流从钢轨泄漏至大地,电流密度为正值,且距牵引变电所的距离越远,电流密度越大。在同一区间内,走行轨泄漏电流密度和埋地金属泄漏电流密度的变化趋势相反。
2.2 双层土壤模型
为了对杂散电流在双层土壤中的变化进行研究,在机车与变电所距离为1 000 m内,分别对土壤电阻率随深度增大的变化情况(模型D)、随深度减小的变化情况(模型E)与相对于模型D下层土壤电阻率不变上层电阻率增大的情况(模型F)进行分析。
图8所示为模型D、E、F中杂散电流和变电所距离之间的关系。由图8可知,在0~500 m范围内,距牵引变电所距离增大,杂散电流也增大;在500~1 000 m范围内,距牵引变电所距离增大,杂散电流反而减小,对应的极值分别为0.244 1、0.027 2、0.061 0 A。将模型D与模型F进行对比可知,下层土壤电阻率一定时,上层土壤电阻率的降低会导致杂散电流的增大。
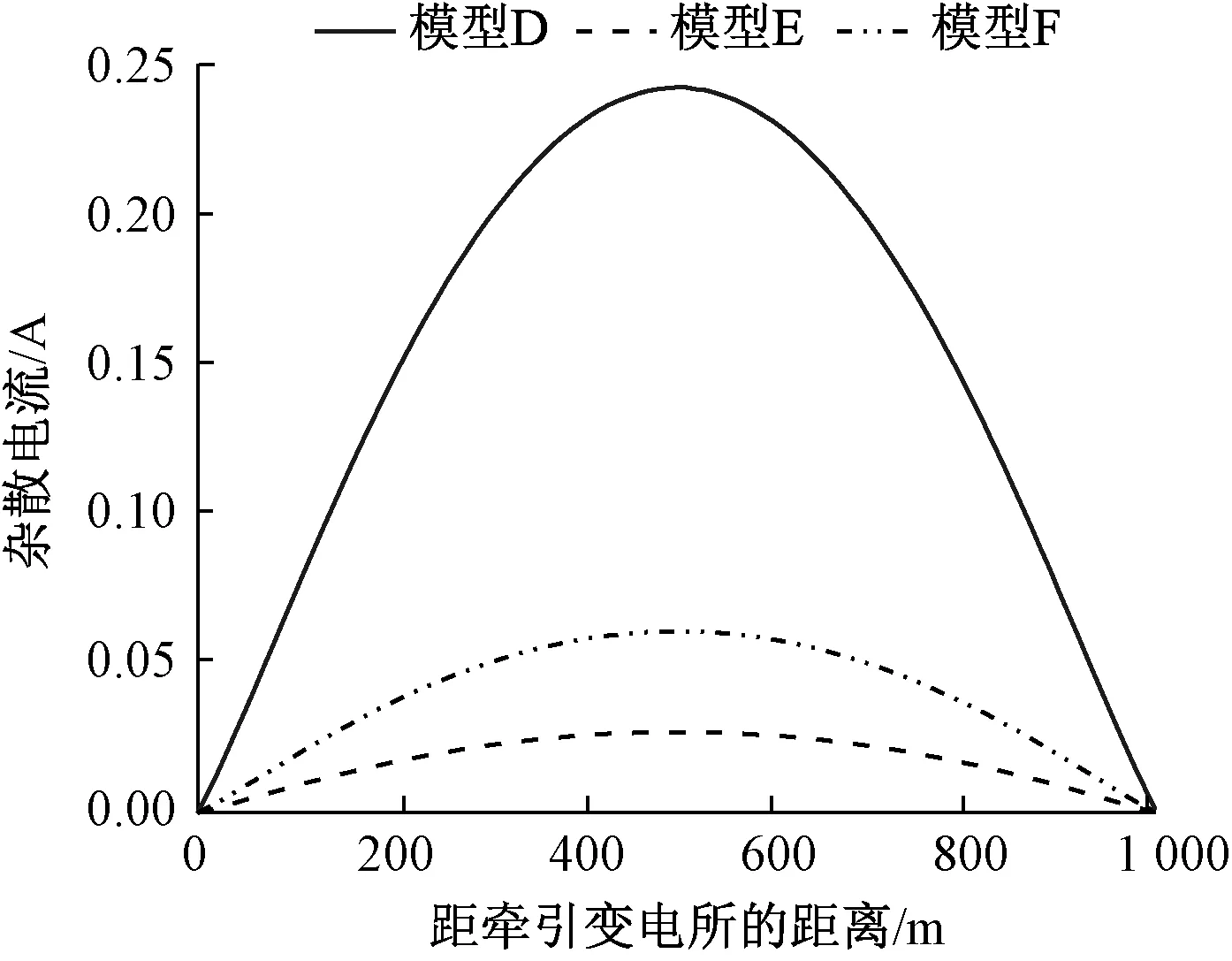
图8 双层土壤模型中杂散电流分布
图9给出了6种不同模型杂散电流在大地、排流网和埋地金属中所占的百分比。将模型A与模型D进行对比可知,当底层土壤电阻率从100 Ω·m增大到1 000 Ω·m时,杂散电流占比增大,即排流网电流收集率增加;将模型B与模型F进行对比可知,当底层电阻率从300 Ω·m增大到1 000 Ω·m时,杂散电流占比也有所增加,但增加的幅度降低,即排流网电流收集率增加的幅度降低。

图9 杂散电流占比
将模型C与模型E进行对比可得,当下层土壤电阻率由1 000 Ω·m降低到100 Ω·m时,排流网收集率几乎不变。如果上层和下层土壤电阻率差值较大,例如在模型E中,则杂散电流将泄漏不到下层土壤中。因此,在模型E中,杂散电流难以泄漏到有埋地金属的下层土壤中以及土壤电阻率较低的土壤中,这一结论与土壤电阻率为1 000 Ω·m的均匀土壤(模型C)的结论相一致。
除此以外,从图9还可以看出,模型C和模型E排流网的杂散电流收集效率差异较小,埋地金属管道上的杂散电流也没有明显的变化;将模型A与D进行对比分析可得,排流网的电流收集率随下层土壤电阻率的增加而增大,因此流过埋地金属管道的杂散电流会减少。
3 实验验证
3.1 实验方法
为了对本文建立的杂散电流模型的合理性进行验证,搭建了如图10所示的杂散电流实验测试平台。其中,直流电源选用FT10010型费思泰克线性直流电源,其输出电压为0~100 V,输出电流为0~10 A,其作用相当于牵引变电所;选用10个1 Ω(P=10 W)的水泥电阻串联仿真走行轨,其电阻值为33.33 Ω/m,该值远大于实际牵引系统中走行轨纵向电阻值,目的是为了增大杂散电流的值以提高测试精度[20];将长为7 cm的探针一端焊接在相应节点上,另一端直接插入土壤,每两个探针相隔3 cm,机车距牵引变电所的距离为30 cm。将VICTOR 98A+型电压表负极与土壤相接,正极依次与图10中节点1至节点11相接,可测得各节点与土壤之间的电压值。用FLUKE 8846A型台式高精度万用表测量牵引电流(分别为1、2、3 A)流过节点1~11时产生的泄漏电流I1~I11。
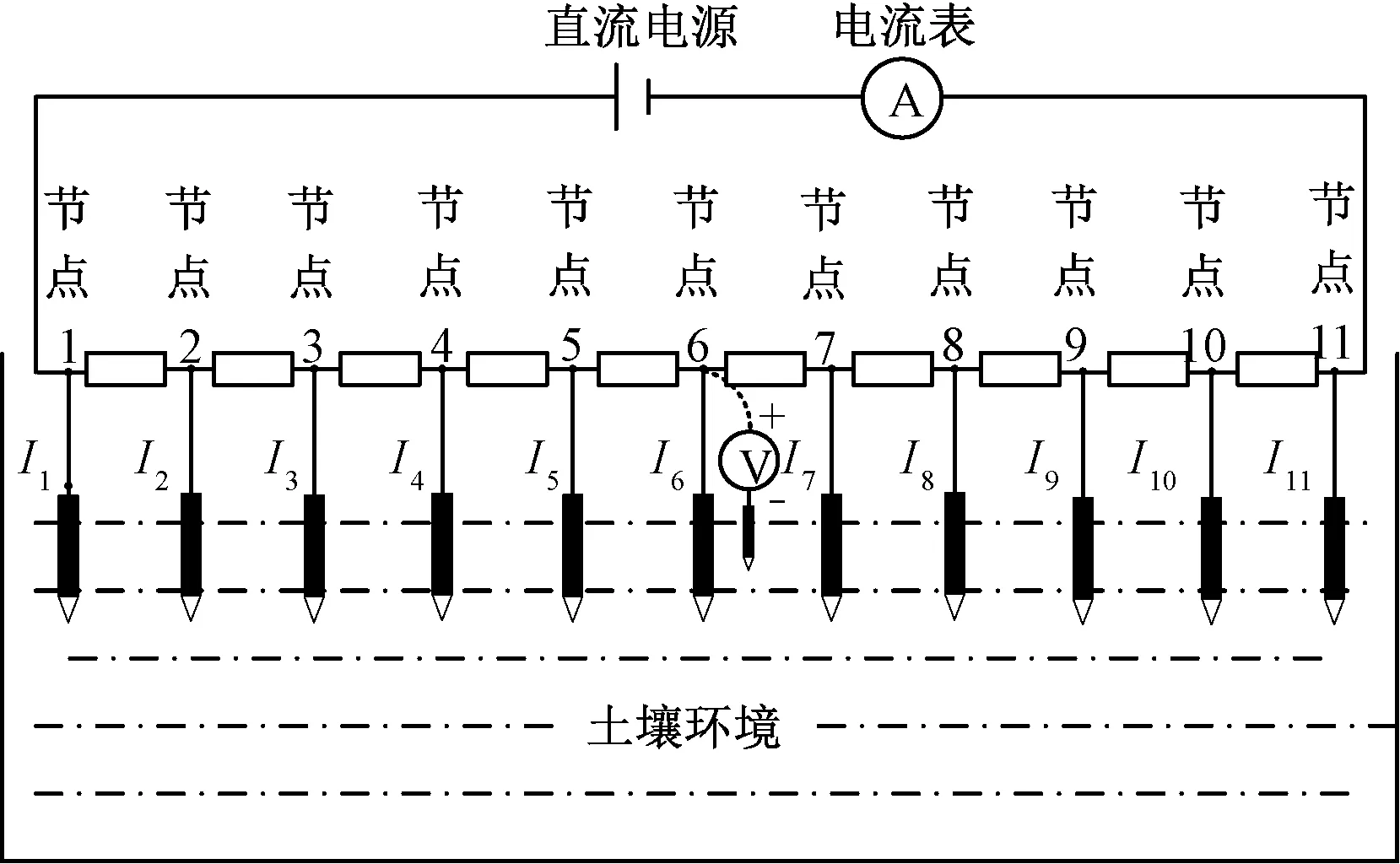
图10 杂散电流实验测试原理
土壤电阻率实验测试原理如图11所示[21],用以测量土壤样品的电阻率。图11中,长方体侧面材料为绝缘树脂玻璃,上下底面材料为黄铜板(公共电极的尺寸为20 cm×22 cm,测量电极为15 cm×17 cm,辅助电极为5 cm×8 cm)。长方体的高为25 cm。测量时将被测土壤放入长方体即可。
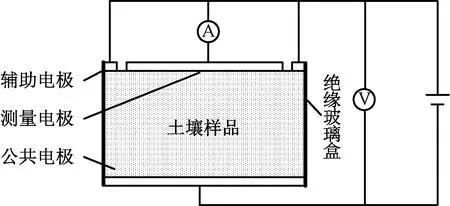
图11 土壤电阻率实验测试原理
由电阻定律R=ρL/S和欧姆定律I=U/R可得土壤样本的电阻率为
( 2 )
式中:S为测量电极面积,m2;U为土壤样本所加电压,V;ρ为土壤电阻率,Ω·m;L为上下极板之间的距离,m;I为流过土壤样本的电流,A。
3.2 实验结果和仿真结果对比分析
CDEGS仿真中,走行轨纵向电阻取实测值33.33 Ω/m,土壤电阻率取值为130.93 Ω·m,该值为测量值的平均值,实验结果和仿真结果的对比如图12所示。
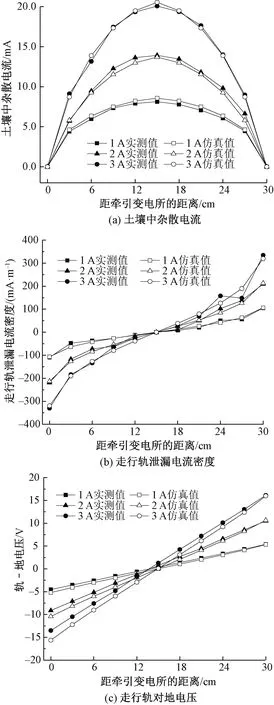
图12 仿真结果与实验结果比对
由图12可知,杂散电流、钢轨(走行轨)泄漏电流密度的实验结果和仿真结果相差很小。钢轨泄漏电流密度最大相差值小于或等于11.49 mA/m,最大相对偏差值为13.65%;杂散电流最大相差值小于或等于0.819 9 mA,最大相对偏差值为14.11%。主要原因为:实验测量值与仿真参数之间有一定的偏差;电阻阻值受实验中产生热量的影响而发生改变。在图12(c)中,轨-地电压仿真结果与实测结果基本吻合,但在距变电所15 cm处,由于土壤样本电阻率分布不均匀,致使该点处轨-地电压值不为零,从而导致零点前移,最大数值相差不超过2.11 V,相对偏差为13.51%。
通过将仿真结果与实测结果对比分析可知:本文采用HIFREQ模块对轨-地过渡电阻和钢轨进行处理的方法与工程实际更接近。要使土壤模型和导体的三维空间拓扑结构设置更合理、计算结果更准确,还需依据现场实际修正计算模型。
3.3 不同土壤类型对比分析
为了研究不同土壤类型对杂散电流的影响,在实验室选用3种不同土壤电阻率的土壤(电阻率分别为130.93、162.65、208.32 Ω·m)分别进行单层均匀土壤、双层土壤的实验测试,测试结果如图13所示。由图13可知:无论对于单层均匀土壤还是双层土壤,随着机车距牵引变电所距离的增大,土壤中的杂散电流呈先上升后下降的变化趋势,且在机车距牵引变电所15 cm处取得最大值,这与图6的仿真结果变化特征一致。在机车距牵引变电所的同一位置处,土壤电阻率较小的单层均匀土壤中杂散电流值要高于土壤电阻率较大的双层土壤中的值。
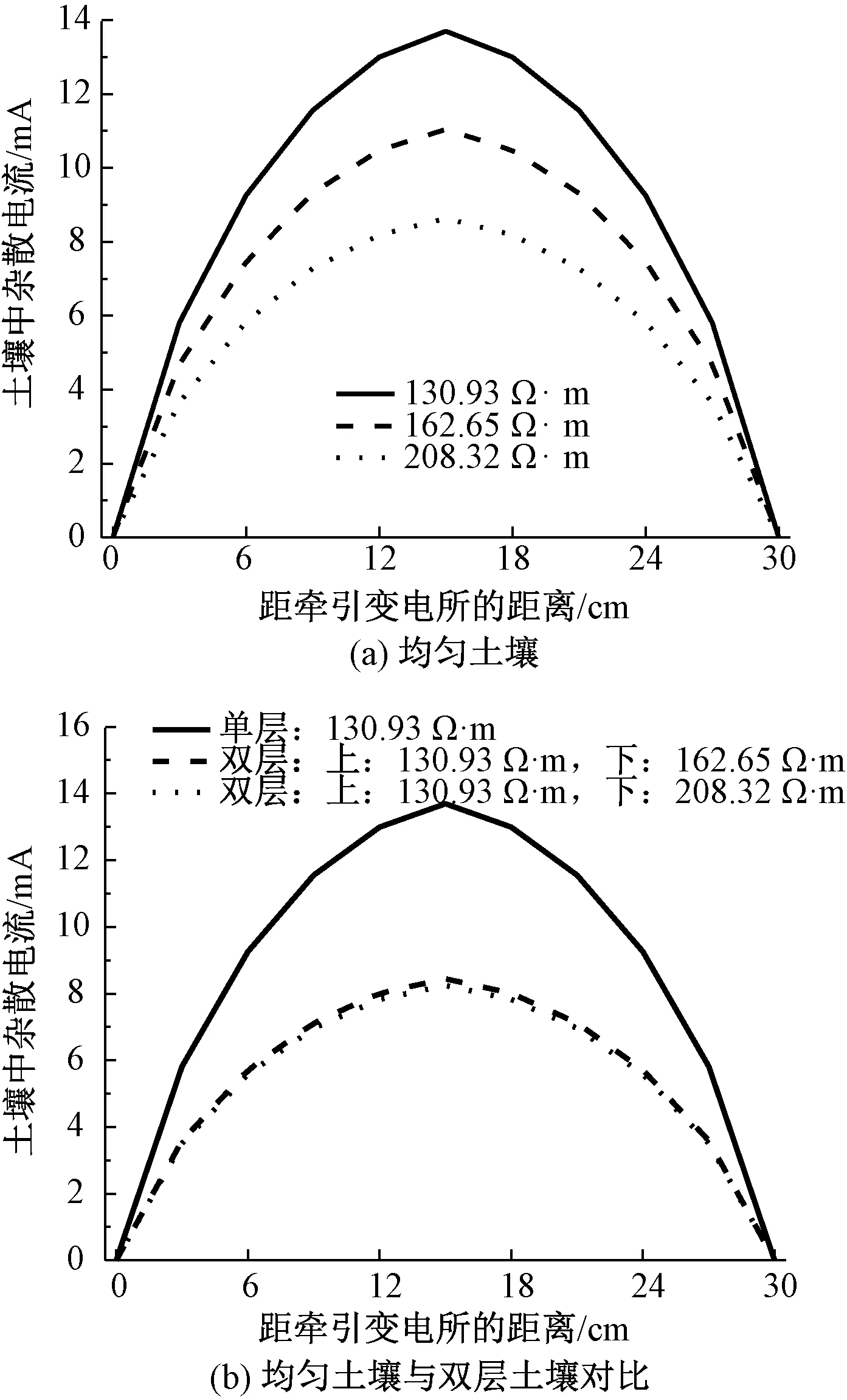
图13 不同土壤类型对杂散电流的影响
4 结论
(1)轨-地电压几乎不受土壤结构的影响,其大小取决于回流电流和钢轨纵向电阻。
(2)在均匀土壤中,杂散电流随土壤电阻率的增大而减小。因此,在工程实际中应尽量增大土壤电阻率,从而降低金属腐蚀。
(3)与均匀土壤相比,在双层土壤中电阻率随土壤深度增加而增大的情况下,排流网的电流收集率明显增大,从而显著降低埋地金属的腐蚀风险。
(4)通过实验室测试距牵引变电所不同距离处土壤中杂散电流、走行轨泄漏电流密度以及走行轨对地电压值,验证了利用CDEGS软件中的HIFREQ模块对直流牵引供电系统进行建模的合理性和计算的可靠性。
