放宽条件下基于定点集结模式的技术站车流接续模型

薛 锋，范千里，陈崇双

(1.西南交通大学 交通运输与物流学院，四川 成都 611756；2.西南交通大学 综合交通大数据应用技术国家工程实验室，四川 成都 611756；3.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 611756；4.宁波港铁路有限公司，浙江 宁波 315200；5.西南交通大学 数学学院，四川 成都 611756)

定编集结和定点集结是我国铁路运输采用的两种货车集结模式。其中，定编集结能够充分利用机车车辆和线路的通过能力,定点集结有利于维护列车运行秩序，保障货物运到期限。两种模式各有利弊。随着货物运输市场化的快速发展，铁路货车的周转效率以及技术站的工作组织应达到更高标准。放宽条件下的定点集结指车列在规定时间达到最小列车编成辆数即可集结完毕，这种模式能够兼顾定编和定点集结的优势，逐步受到铁路运输部门的重视。

放宽条件下的定点集结模式，核心问题在于最小编成辆数，目前国内的学者在这方面的研究较多。李静等[1-2]建立了描述车辆在调车场集结过程的批到达批服务排队模型，并从经济角度求得最优最小编成辆数；王如义[3]测度了不同发车模式给编组站带来的运输成本改变，并以此给出最优最小编成辆数的计算公式；林枫[4]通过比较不同集结模式的经济效益，得到不同集结模式的经济适用条件；刘晨等[5]从经济的角度计算列车最小编成辆数，并以编组站有调中转车停留时间最小为目标，优化到达列车解体顺序；李红雨[6]基于差量成本，将以运行图为基础的定点集结方案与以班计划为基础的集结方案进行比较；李建文[7]通过以山海关至济南西及其以远去向的车流集结过程为例，模拟定编、定点集结，并指出相较于定编集结，定点集结能够有效降低列车晚点出发的时间和概率。国外学者单纯对列车编成辆数的研究较少，主要集中在编组站的作业优化方面。Boysen等[8]分析技术站列车编组问题的复杂性，在掌握到达解体列车进站、解体顺序以及出发列车编组数量的基础上，利用启发式算法给出调车线集结货车最优编组决策；Adlbercht等[9]考虑适用于调车场内移动的所有约束条件，建立目标为调车机车最佳路线的混合整数规划模型，并进行实例分析；Bohlin等[10]提出了微观层面的货运场规划运筹学方法，考虑实际的货车移动和调车操作，讨论它们在德国路德维希港和瑞典哈尔斯贝格调车场中的应用；Bilg等[11]针对技术站配流问题，提出两种不同的整数规划模型进行求解，并通过随机鲁棒的建模方法扩展了模型。

上述研究大多数从经济效益的角度，运用不同的方法分析列车编成辆数，但若某方向到达车流较少，无法达到最小编成辆数，势必会导致该方向下游技术站车流接续逐步出现不足。实际上，为了避免这种情况，从路网的角度出发，上游技术站应有一个最小编成辆数，以便随着列车逐渐运行而使其编组数量不断增加。由此，本文从欠轴列车的经济影响和区域路网车流接续两个角度出发，建立放宽条件下基于定点集结模式的技术站车流接续模型，并进行验证分析。

1 欠轴列车开行的影响分析

若某方向列车在规定的出发时刻未能集结满轴，在放宽条件下定点集结模式中是否对其做出丢线处理，需要考虑两个方面：①本站开行的损耗及收益；②对下游技术站车流接续的影响。前者决定了本站不同方向出发列车的最小编成辆数，后者决定了列车在不满足最小编成辆数要求时是否继续开行。

1.1 欠轴列车开行损耗及收益分析

铁路运输企业在保证货物准时性、便利性的同时，还要考虑企业自身的经济效益。因此，在放宽条件下的定点集结模式中，欠轴列车开行的必要条件是收益大于损耗。

(1)开行欠轴列车损耗分析

由于欠轴列车无论是丢线还是继续开行，总的车辆数是相同的。因此，相比于丢线，开行欠轴列车的主要成本集中于机车及线路能力损耗，包括两个方面：①由于列车编成辆数的减少导致机车及列车运行成本增加；②下游编组站分解车列的次数增多，从而增加了调机的作业成本。k方向开行欠轴列车的成本Ck[3,12-13]为

(1)

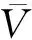
(2)开行欠轴列车收益分析

开行欠轴列车的收益主要体现在线路能力利用方面，相比于丢线处理，开行欠轴列车则利用了部分线路能力。k方向开行欠轴列车的收益Qk为

(2)

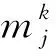
基于以上分析，在放宽条件下定点集结模式中，k方向的最小编成辆数应使欠轴列车的收益大于损耗，即

Qk≥Ck

(3)

根据以上方法可以确定不同方向欠轴列车的最小编成辆数，若欠轴列车满足最小编成辆数要求，则仍可发车，若未达到最小编成辆数要求，则需要分析欠轴列车对下游技术站的影响,以确定是否发车。

1.2 对下游技术站的影响分析

(1)欠轴列车开行的判定

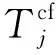
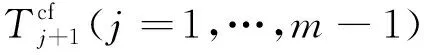
(4)

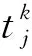
(2)下游技术站车流接续不足时长的描述

下游技术站的车流接续情况与车流量有直接关系，车流量的大小决定了是否会出现车流接续不足的情况。在没有上游技术站车流补充的情况下，类似于传统的可靠性分析。因此，引入装备可用度理论描述前方技术站车流接续充足的期望时长。装备可用度理论是度量系统性能好坏的指标之一，它表示任一时刻系统处在正常状态的概率，目前广泛运用于可靠性工程、装备综合保障、信息技术产业、交通运输等领域。对于技术站而言，可以将其视为一个装备系统，其中包含的与技术站技术作业相关的一切实体都可以视为技术站的子系统，如到达系统、解体系统、集结系统、编组系统、出发系统等。

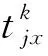
j=1,2,…,mk=1,2,…,K

(5)

(6)

δ(m′j)=(1+m′j)·e(-m′j)

j=1,2,…,m

(7)

j=1,2,…mk=1,2,…,K

(8)

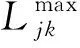
对于F(t)的取值，若直接采用统计得到的前方技术站系统车流接续充足的时间序列Tk=[t1,t2,t3,…,tz]作为概率,z为统计得时间序列数量，则无法反映随着车流量的逐渐减少，下游技术站车流接续充足的期望时长逐渐降低的过程，以及随着上游技术站逐渐对下游技术站进行车流补充，下游技术站车流接续充足的期望时长逐渐增加的过程；另一方面，F(t)在可靠性研究中，可以采用的模型较多，如二项分布、泊松分布、正态分布、威布尔分布等。其中，威布尔分布在描述系统可靠性方面运用较多，且威布尔分布是根据串联模型得到的，具有递增的失效率，车流接续充足的期望时长随着车流缺口数量增加、影响范围扩大及程度加深，两者之间具有很大的相似性，且在现有的技术站可靠性研究中也有一定的运用，具有较好的适应性。

因此，本文采用威布尔分布对其进行描述。为求得λ和γ的取值，采用极大似然估计进行威布尔分布的参数估计。统计得到前方技术站系统车流接续充足的时间序列为Tk=[t1,t2,t3,…,tz]，根据该时间序列[15]可得λ和γ的取值为

(9)

(10)

(11)

(12)

2 模型建立

2.1 参数及目标函数

为便于建模，设定基本条件和假设：

(1)该技术站2台调机进行解体作业，1台调机进行编组作业。

(2)技术站内各车场线路均满足接发列车作业要求。

(3)不考虑无调中转车及其在站的甩挂作业。

(4)不考虑调机故障、调机整备及调机维修情况。

相关参数含义及取值见表1。

表1 参数及其符号说明

变量及符号说明见表2。

表2 变量及其符号说明

根据技术站车流接续的实际情况，放宽条件下基于定点集结模式的目标设置为货车在技术站内平均的停留时间最短，即

(13)

2.2 模型的约束条件

(1)解体作业约束

①任一id只能由一台解体调机进行解体作业。

(14)

②任一id的解体作业必须在到达作业之后进行。

(15)

③由同一解体调机进行解体的任两列到达列车不能存在作业时间冲突

(16)

④任意两列车不由同一解体调机进行解体作业时，只有前一列车完成解体作业后，另一列车才能开始解体。

(17)

(2)车流量约束

任一id的k方向重、空车在各出发列车与阶段末残存车之间的车流守恒。

(18)

(19)

(3)车流接续约束

(1)深一含粉细砂压缩层(B5)：处于该层组顶部，由细砂及粉细砂层组成，底板埋深80～100 m，厚度10～20 m，一般呈中密～密实状态。

①任一jc只能吸收解体结束时间小于该列车编组开始时间的到达列车车流。

1≤i≤n1≤j≤mk∈K

(20)

②任一jc只能吸收编组去向相同的到达列车车流。

Nikj≤M·Bjk1≤i≤n1≤j≤mk∈K

(21)

(4)编成辆数约束

任一出发列车长度及重量存在限制。

(22)

(23)

3 模型求解

放宽条件下基于定点集结模式的技术站车流接续模型为非线性混合整数规划模型，通常采用启发式算法求解。为降低求解难度，将问题分解为列车解体编组顺序子问题以及车流来源推算子问题两个部分，结合技术站各项作业时间参数(如到达列车最早解体时刻、出发列车最晚编组时刻等)，分别求解。采用遗传算法对列车解体编组顺序进行求解，运用拉格朗日松弛算法对车流推算子问题进行求解。

3.1 遗传算法求解列车解体编组顺序

(1)染色体编码及初始种群的产生

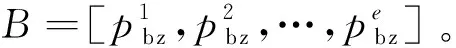
…pe]。

(2)适应度函数设置

在得到初始种群后，运用拉格朗日松弛算法求解得到各列车解体编组顺序下目标函数的大小，并将各染色体的适应度函数设置为各个列车解体编组顺序下的目标函数大小。

(3)遗传算子

运用联赛选择规则选择适应度较大的个体。为防止不合法个体的产生，仅对种群J进行交叉及变异操作；对于种群P中的B，由于对其进行交叉变异易产生非法个体，且初始生成的个体编组顺序基因得到的求解质量和效率较优，因此不对其进行交叉变异操作。本文中交叉算子采用基于位置的杂交算子，变异算子采用散播变异算子。

(4)静态配流

对于静态配流的操作方法，在3.2节拉格朗日松弛算法求解车流推算中进行论述。

(5)终止规则

将进化代数作为算法的停止条件。

3.2 拉格朗日松弛算法求解车流推算

利用车流推算子问题的特殊结构，设计拉格朗日松弛算法，以有效求解该问题。

(1)问题的分解

利用拉格朗日松弛算法的基本原理，将困难约束松弛到目标函数当中。分析该问题的结构可以发现，现有问题的难点在于最小编成辆数的约束下，导致不同的欠轴出发列车可能会采用不同的处理方式，从而增加了问题的求解难度。为此，将约束式(22)、式(23)作为困难约束，引入拉格朗日乘子向量

(24)

(25)

(26)

(27)

分别松弛该两项约束，并将其添加到目标函数中作为惩罚项，原问题转化为

(28)

s.t. 式(14)～式(21)

(29)

式中：θj为jc中重车的比重。

若已知拉格朗日松弛算子ω1、ω2、ξ1、ξ2，对松弛问题的目标函数

(30)

(31)

则可以将松弛问题的目标函数进一步进行重新表述，得到

minz(ω1,ω2,ξ1,ξ2)=

(32)

由此松弛问题可描述为

目标函数：式(32)。

s.t. 式(14)～式(21)

将松弛问题的目标函数式(32)与原问题的目标函数式(13)相比，假设拉格朗日松弛算子ω1、ω2、ξ1、ξ2已知的条件下，目标函数的结构基本相同，且原问题的最优解同样可以作为松弛问题的可行解，但松弛问题的可行解，或最优解不一定是原问题的可行解。因此，在已知解体编组顺序以及各类时间参数的情况下，相比于原问题，松弛问题就是去掉了编成辆数约束的车流推算问题。

(2)可行解

运用拉格朗日松弛算法求解时，需要确定理论上界以及理论下界，从而得到相对最优解。

①理论上界的求解

在解体编组顺序确定的条件下，可以得到列车最早解体开始时刻以及最晚编组开始时刻，原问题可以变为简单的车流推算问题。该类问题可以采用广义静态配流的搜索算法求解。同时，可以发现，若给定了各列车的最早解体开始时刻以及最晚编组开始时刻，则原问题中解体作业约束以及编组作业约束已经起到了约束作用，运用相关算法求解可以得到一个可行解。这个可行解一定是原问题的一个上界ZUB。

②理论下界的求解

通过问题的分解可以发现，当到了列车运行图规定的发车时刻时，不用考虑列车是否满轴，都可以做发车处理。若不考虑列车是否满轴，货车在技术站的停留时间也会大大减少，因此可以运用相关算法求解得到一个松弛问题的最优解，作为下界ZLB。

在求解得到理论上界和下界后，同时可以确定各个变量的取值。

(3)拉格朗日乘子的更新

拉格朗日松弛算子ω1、ω2、ξ1、ξ2对松弛问题的向下定界有重要作用。通常，乘子的最优值可通过最大化对偶问题得到，对偶问题为

maxz(ω1,ω2,ξ1,ξ2)

s.t.ω1,ω2,ξ1,ξ2≥0

(33)

然而，松弛问题的目标函数是关于拉格朗日松弛算子ω1、ω2、ξ1、ξ2的分段性凸函数，连续不可微。因此，采用次梯度算法进行乘子的更新。

(4)拉格朗日松弛算法的步骤

Step1初始化。

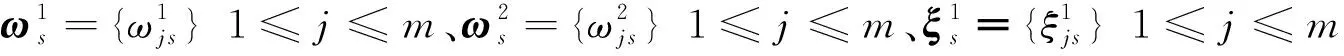
Step2终止条件。

根据迭代终止的原则，若(ZUB-ZLB)/ZLB≤τ，则认为算法终止，输出最优解；否则，令s=s+1，继续执行Step3至Step5中的相关步骤，重新更新相关结果后执行Step2。

Step3最优上界的计算。

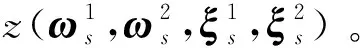
Step4最优下界的计算。

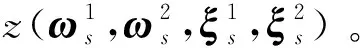
Step5更新拉格朗日乘子。

拉格朗日乘子更新方式为

(34)

式(34)中，步长ts的更新为

(35)

(36)

在式(35)中，若最优下界ZLB连续停留在某个值的次数超过α次，可以将λs的值减半；若最优上界ZUB被成果进行了更新，可以将λs的值恢复为2。

4 算例分析

4.1 基础数据

某技术站衔接3个方向，可集结和编组6个去向的车辆。其中，每个方向都有3个去向，所有的去向根据其方向，由远至近依次进行编号。例如，东方向的去向，由远至近依次可以被标记为1、2；同理，西方向的去向由远至近依次被标记为3、4。根据本文建立的模型，前方各方向区间及技术站数据、费用计算等参数见表3、表4。

表3 前方各编组去向区间及技术站数据

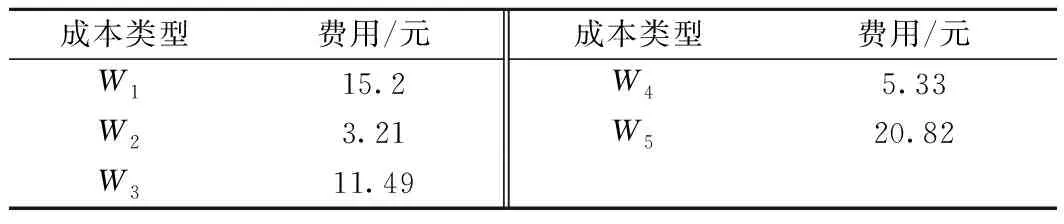
表4 费用计算表

8:00—12:00时间阶段，具体的车流到达信息见表5。

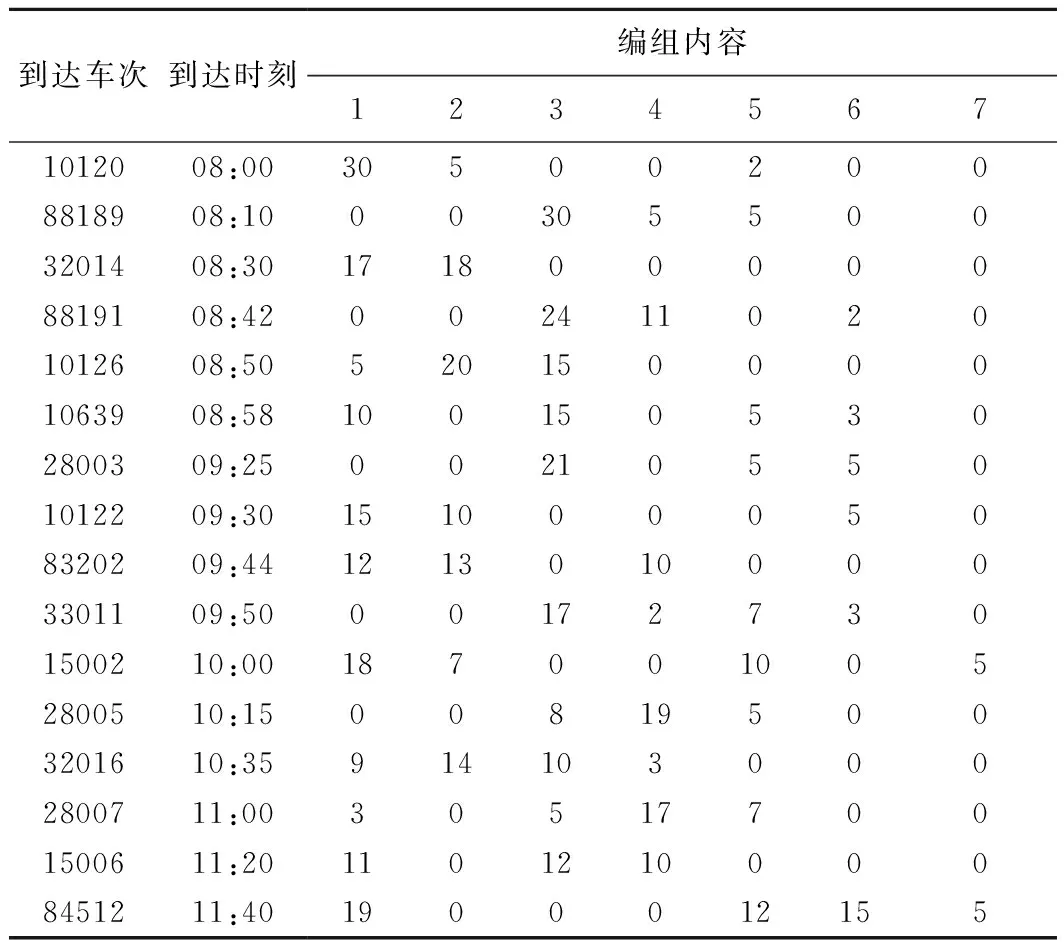
表5 到达列车车流信息

设列车到达技术作业时间及出发技术作业时间为30 min，列车解体技术作业时间及编组技术作业时间为15 min，出发列车的最小总重、最大总重、最小换长、最大换长分别为27 000 kN、28 000 kN、43、45，空车重量为200 kN，重车重量为800 kN。其中，摘挂列车允许欠轴开行，该技术站拥有解体调机2台，编组调机1台。根据车站作业组织情况统计，出发列车所在时段比到达列车晚2 h。因此，选取10:00—14:00的出发列车，具体车流信息见表6。

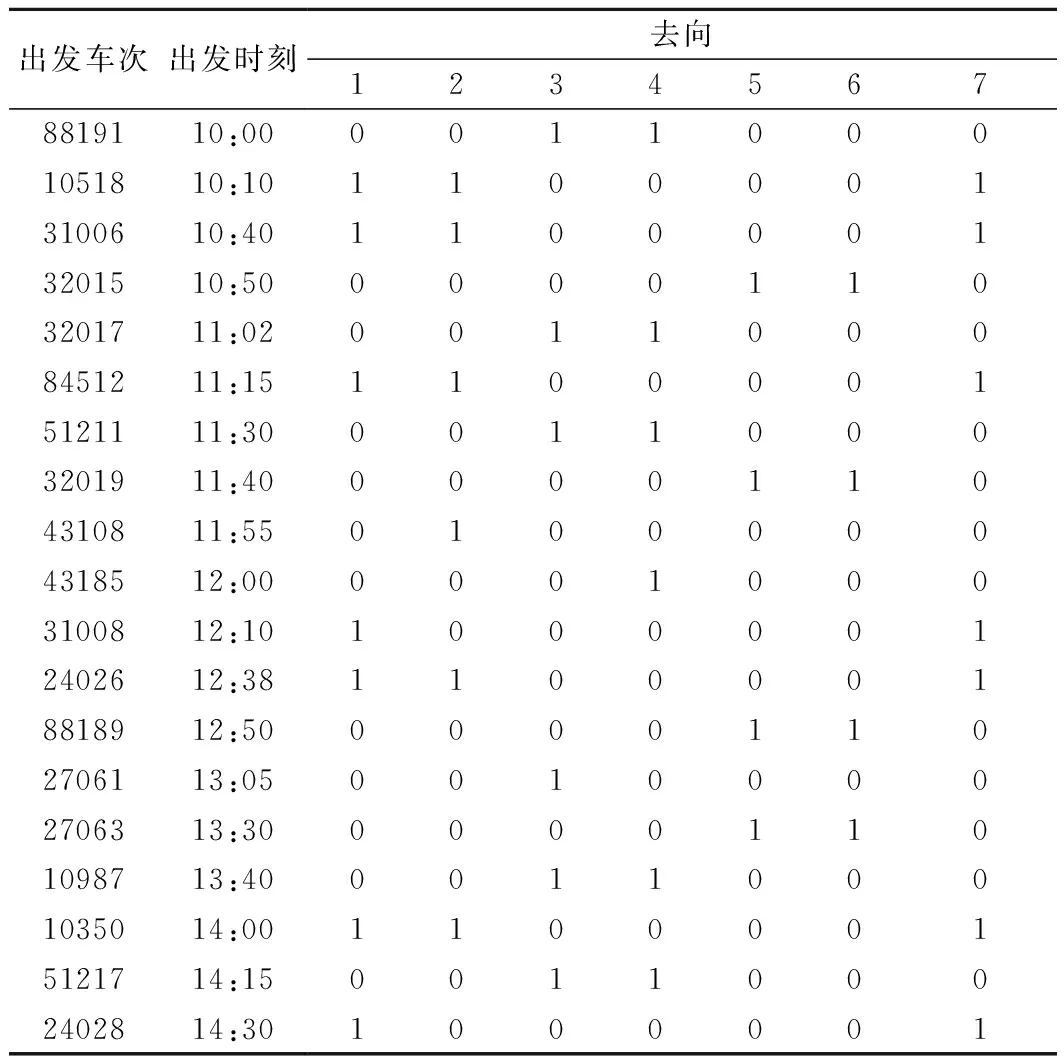
表6 出发列车车流信息

4.2 算例求解

首先对技术站到达与出发车流运用传统的配流方法进行配流，到达列车的解体顺序为[1,2,3,4,5,6,8,7,9,12,11,10,13,14,15,16]，出发列车编组顺序为[2,1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]，得到配流方案见表7，各方向下游技术站车流接续充足的期望时长见图1。

表7 优化前配流方案

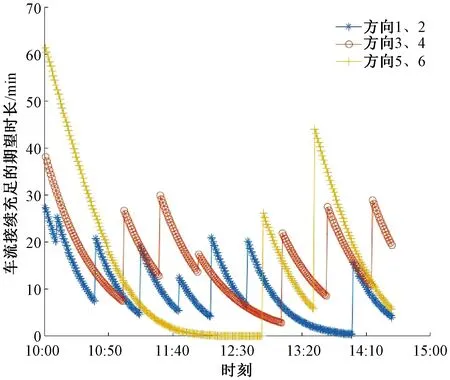
图1 优化前各方向下游技术站车流接续充足的期望时长

在配流方案中，该技术站货车停留时间为1 785.3 h，货车的平均停留时间为187.6 min。

分析优化前的配流方案可以发现，当前的配流方案存在着较大的不足，出发列车11101次、11103次列车都由于车流接续不足而出现丢线的情况。在阶段结束后，调车场内存在残存车，且对于技术站衔接区段的下游技术站，优化前的5、6方向出现了车流接续不足的情况。以上情况的发生都降低了技术站货车转移的效率，为此，采用本文建立的模型及算法对配流计划进行优化。设置交叉概率为0.1，变异概率为0.01，最优误差为0.01，迭代次数为100，可以得到基于放宽条件下定点集结模式下到达列车的解体顺序为：[1,2,3,4,6,5,7,8,9,12,11,10,13,14,15,16]，出发列车编组顺序为[2,1,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]，得到优化后各方向下游技术站车流接续充足的期望时长见图2，优化后的配流方案见表8。

表8 优化后配流方案

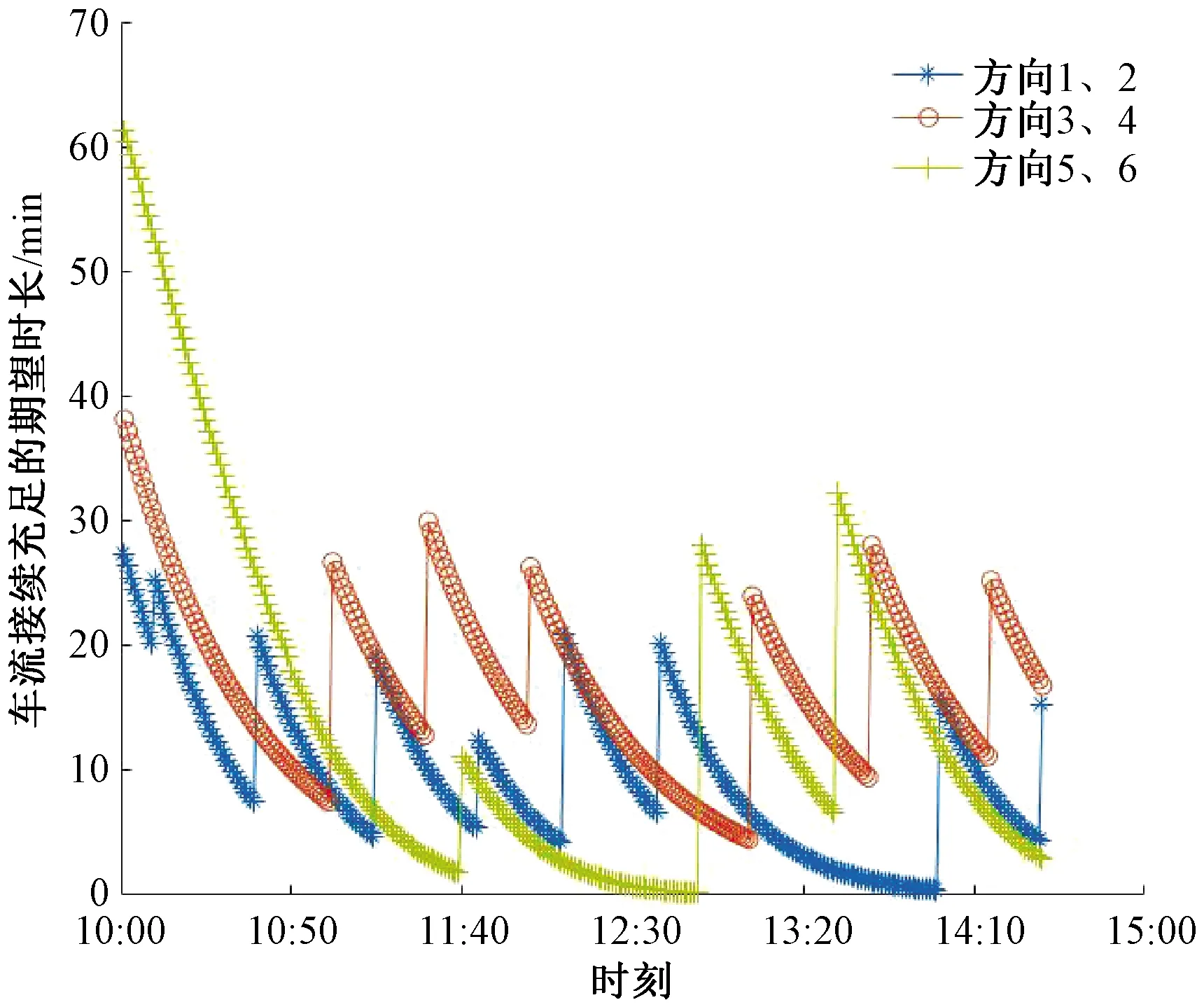
图2 优化后各方向下游技术站车流接续充足的期望时长

在优化配流方案中，技术站内货车停留总时间为1 521.8 h，货车在技术站内的平均停留时间为159.9 min。

对比优化前后技术站的配流方案以及技术站所衔接区段各方向的下游技术站车流接续充足的期望时长，可以发现：运用本文模型对原有的车流接续计划进行优化，改变了技术站内列车的解体编组顺序，并基于放宽条件下的定点集结模式，放宽了编成辆数要求，在优化前配流方案中存在11101、11103、11216次列车出现丢线的情况，且调车场内存在残存车。在优化后，配流方案中仅11101次列车出现了丢线情况，调车场内也不存在残存车，货车平均在站停留时间减少了15%。同时，不但减少了列车丢线的情况，并且使技术站所衔接区段的下游技术站出现车流接续充足的期望时间增加。在算例中，优化前5、6方向技术站在12：00左右出现车流接续不足，而在优化后5、6方向没有出现车流接续不足的情况，有效提高了本技术站及下游技术站的货车整体转移效率。

结合1.1节中列车开行损耗及收益的计算方法，基于表3、表4以及优化前后的配流结果，可以得到优化前后列车开行收益与损耗的差值，即净收益，见图3。

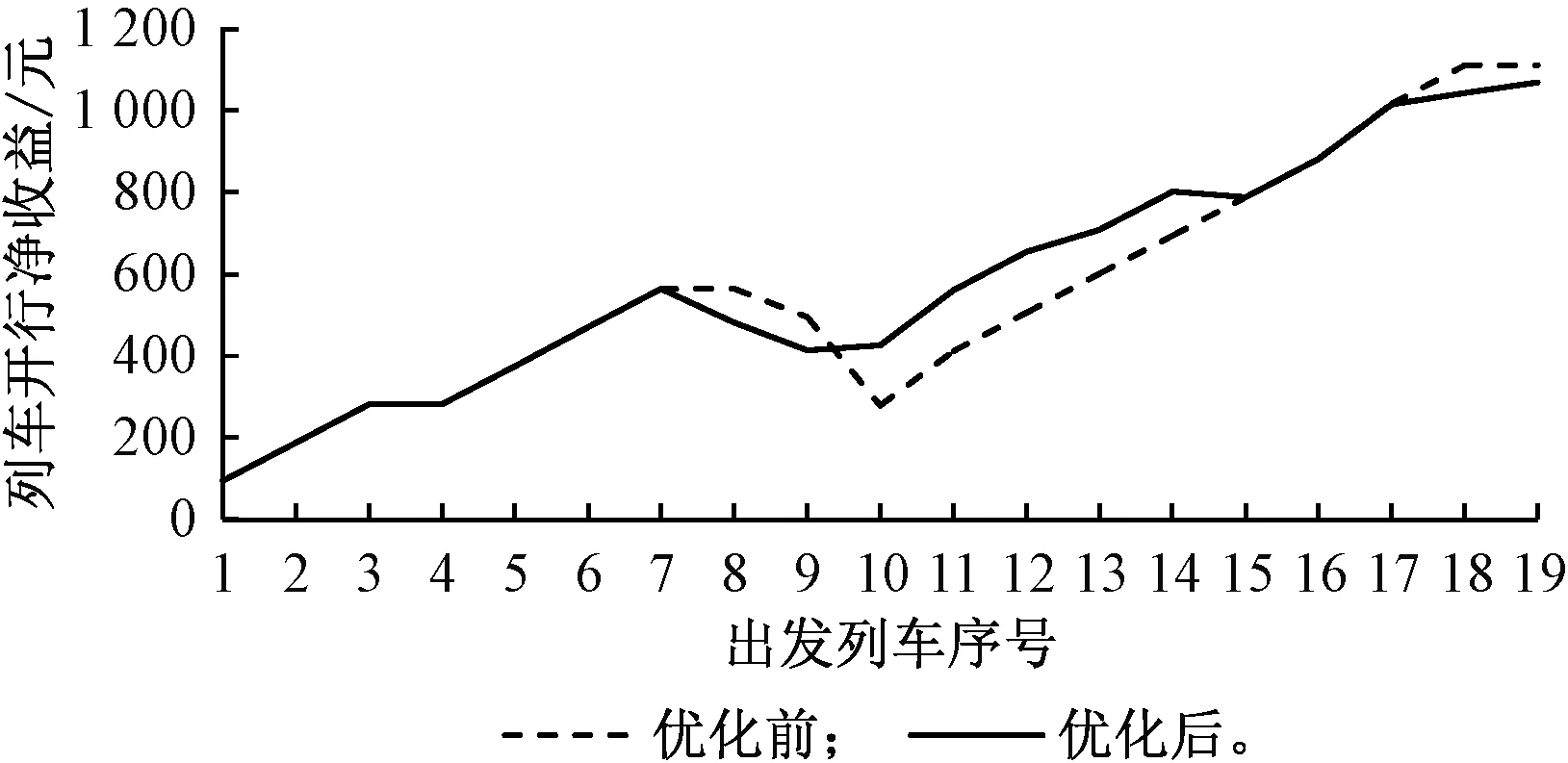
图3 优化前后列车开行净收益

优化前列车开行净收益为1 110.83元，在摘挂列车43108以及43185开行后，由于摘挂列车无视最小编成辆数约束，列车开行的净收益出现了较大的下滑，而其他列车的开行使得净收益能够稳定增长；在优化后列车开行净收益为1 068.61元，虽然优化后下游技术站没有出现车流接续不足的情况，提高了本技术站以及下游技术站整体的货车转移效率，但由于开行了多列欠轴列车，且考虑下游技术站的车流接续情况而开行了多列低于最小编成辆数的欠轴列车，因此列车开行的净收益相较于优化前有所下降。

5 结论

本文在放宽条件下基于定点集结模式，考虑欠轴列车开行相比于丢线处理的经济性以及对下游技术站的影响，建立技术站车流接续模型，通过算例验证，得到以下结论：

(1)欠轴列车开行的必要条件可以从两个方面确定，具备其中之一即可开行：①从列车开行损耗及收益的角度确定不同方向的最小编成辆数，当列车的编成辆数大于最小编成辆数时；②从下游技术站车流接续情况考虑，若列车的丢线将造成下游技术站车流接续不足时，则欠轴列车仍可开行。由于优化后相较于优化前开行了部分欠轴列车，会造成列车开行的净收益减少。

(2)放宽条件下定点集结模式相比于定编集结模式，有更高的适用性，有效降低了丢线情况的发生，并且能够缓解下游技术站车流接续不足的情况，特别是在某方向到达车流较少时，更具有适用性。

(3)采用放宽条件下的定点集结模式，虽然满轴车数相比于定编集结模式较少，但货车平均在站停留时间明显下降，提升了货车的转移效率。算例中显示，采用放宽条件下定点集结模式货车在站停留时间为1 521.8 h，平均在站停留时间为159.9 min，相比于定编集结模式，降低了15%。