考虑填土泊松比变异性的挡土墙失稳概率分析

王雪冰,张 楠,杨跃辉

(1.中国地质科学院研究生院，北京 100081；2.中国地质环境监测院，北京 100081；3.中国地质科学院地质力学研究所，北京 100081)

挡土墙是一种传统的边坡和滑坡支护结构[1-2]，关于土压力计算理论的研究，岩土界的学者从未间断过[3-4]。

库仑土压力理论、朗肯土压力理论是土压力计算中的两大经典理论，但库仑理论只适用于无内聚力的理想散粒体为填土的情况[5]；朗肯土压力理论虽然较库仑理论在黏性土工况下有更好的适用性，但因以Mohr-Coulomb破坏准则为核心，无法考虑中间主应力的影响[6]，使计算结果偏于保守，无法完全发挥土体的材料强度潜力[7]，仍待进一步完善。范文等[8]基于考虑中间主应力效应的统一强度理论，按土压力上限理论和多三角形破坏机构的计算原理推导了基于统一强度理论的土压力公式，但其形式复杂，实际应用较为不便；庄心善等[9]应用广义Hooke定律结合Lade-Duncan屈服准则，得到了考虑中主应力影响的土压力计算公式，且由泊松比来描述中主应力水平，形式简明，对于无黏性填土情况具有较好的适用性，但对具有内聚力填土的适用性尚需考究；胡贺祥等[10]完全基于Lade-Duncan准则推得考虑中主应力的平面应变强度公式，给出土压力计算公式，形式简洁，且对有无内聚力的填土都具有较好的适用性。

以上学者考虑中主应力的影响，提出计算结果更为准确的土压力计算模型，但仍基于填土为完全均匀的假设，无法消除填土内不同部位属性差异的影响。事实上，由于填土组成成分、堆积方式及空间分布的差异性和不均匀性[11]，不同位置填土的物理参数存在不同程度的差异。土体泊松比是一项反映土体侧向变形的重要参数[12]，不同位置填土泊松比的差异性程度在一定程度上可以反映填土的不均匀程度。Wichtmann等[13]通过共振柱试验以及波速试验研究颗粒级配对石英砂泊松比的影响，结果表明泊松比随着颗粒级配不均匀系数的增大而增大；Kumar等[14]通过波速试验研究了干砂泊松比与相对密度的关系，得出泊松比随相对密度的增大而减小；高武平等[15]通过研究天津地区的原位波速测井资料，得出填土的泊松比随深度的增加而增大，且与土层岩性、含水量和孔隙比有较强的对应关系。由此可见，不同位置的填土结构差异越大，其泊松比的变异性越大。目前关于填土泊松比对土压力及挡土墙稳定性影响的研究较少，大部分研究将泊松比作为一个定值，忽略了泊松比的分布差异性和变异性[16]。

基于此，本文在前人考虑中主应力提出的土压力计算模型的基础上，结合相关规范公式[17-18]，给出考虑墙后填土泊松比的挡土墙稳定性分析模型。以稳定性分析模型为基础，将泊松比视为服从均值为测定值、标准差由变异系数控制的正态分布的随机变量，基于Monte Carlo法，建立考虑泊松比变异性的挡土墙失稳概率分析模型。最后通过具体算例分析讨论墙后填土泊松比及其变异性对挡土墙稳定性及失稳破坏概率的影响。以期为墙后填土泊松比变异性对挡土墙失稳破坏概率的影响研究提供参考。

1 土压力计算推导与挡土墙稳定性分析模型

1.1 基本假设

(1)研究土压力时假定填土为表面水平的半无限空间弹性体。

(2)墙后填土位移极小、处于主动极限平衡状态。

1.2 修正的Lade-Duncan破坏准则

Lade准则最初用于描述没有内聚力的散体材料如颗粒状沙土等。1999年Ewy[19]通过引入S和η两个材料参数对Lade准则进行了修正，使其可用于具有内聚力的材料。修正的Lade准则表达式为

(1)

(2)

式中：I′1为应力张量的第一不变量；I′3为应力张量的第三不变量；σ1、σ2和σ3分别表示最大主应力、中主应力和最小主应力。S和η分别与材料的内聚力和内摩擦系数有关，其计算公式为

(3)

(4)

μi=tanφ

(5)

式中：c为内聚力；φ为内摩擦角；μi为内摩擦系数。在修正的Lade-Duncan破坏准则中，若给定内聚力c和内摩擦系数μi，就可确定出两个材料参数S和η。

1.3 主动土压力公式推导

广义Hooke定理[20]中：

(6)

(7)

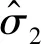
(8)

为方便计算，记α为最小和最大主应力的比值：

(9)

联立式(1)、式(2)、式(7)～式(9)，可整理出一个关于α的一元二次方程：

(1+υ)3α2+[2(1+υ)3-(27+η)υ]α+1=0

(10)

记该方程的解为α1和α2，求解可得

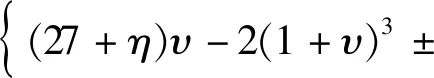
(11)

证得α1∈(1,+∞),α2∈(0,1)。根据主动土压力的定义，主动土压力系数小于1，故主动土压力系数Ka为

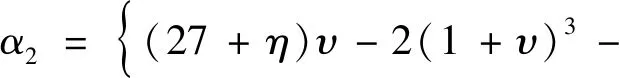
(12)

对于半无限空间弹性体中深度z处的微小单元体，作用在微元体顶面的法向应力σ1方向为竖直方向，侧向应力σ3方向为水平方向，故有

(13)

式(13)中：σz为深度z处的竖向应力；σx为水平向应力；ea为主动土压力。联立式(8)、式(9)和式(13)，整理得

ea-S0=Ka(σz-S0)

(14)

对于填土单元，竖向荷载为

σz=γz+q

(15)

式(15)中：γ为填土重度；q为地面荷载。因此深度z处的主动土压力计算公式为

(16)

对于无黏性土在z处的主动土压力公式，令c=0即可求得。式(16)中，令eaz=0可解得黏性填土的土压力临界深度：

(17)

在临界深度z0以内，墙面不受土压力作用。当z>z0>0时，总主动土压力为

(18)

当z0<0时，总主动土压力为

(19)

式(19)中：ea0为表面处的主动土压力值。

1.4 经典挡土墙模型

所采用的挡土墙模型如图1所示。

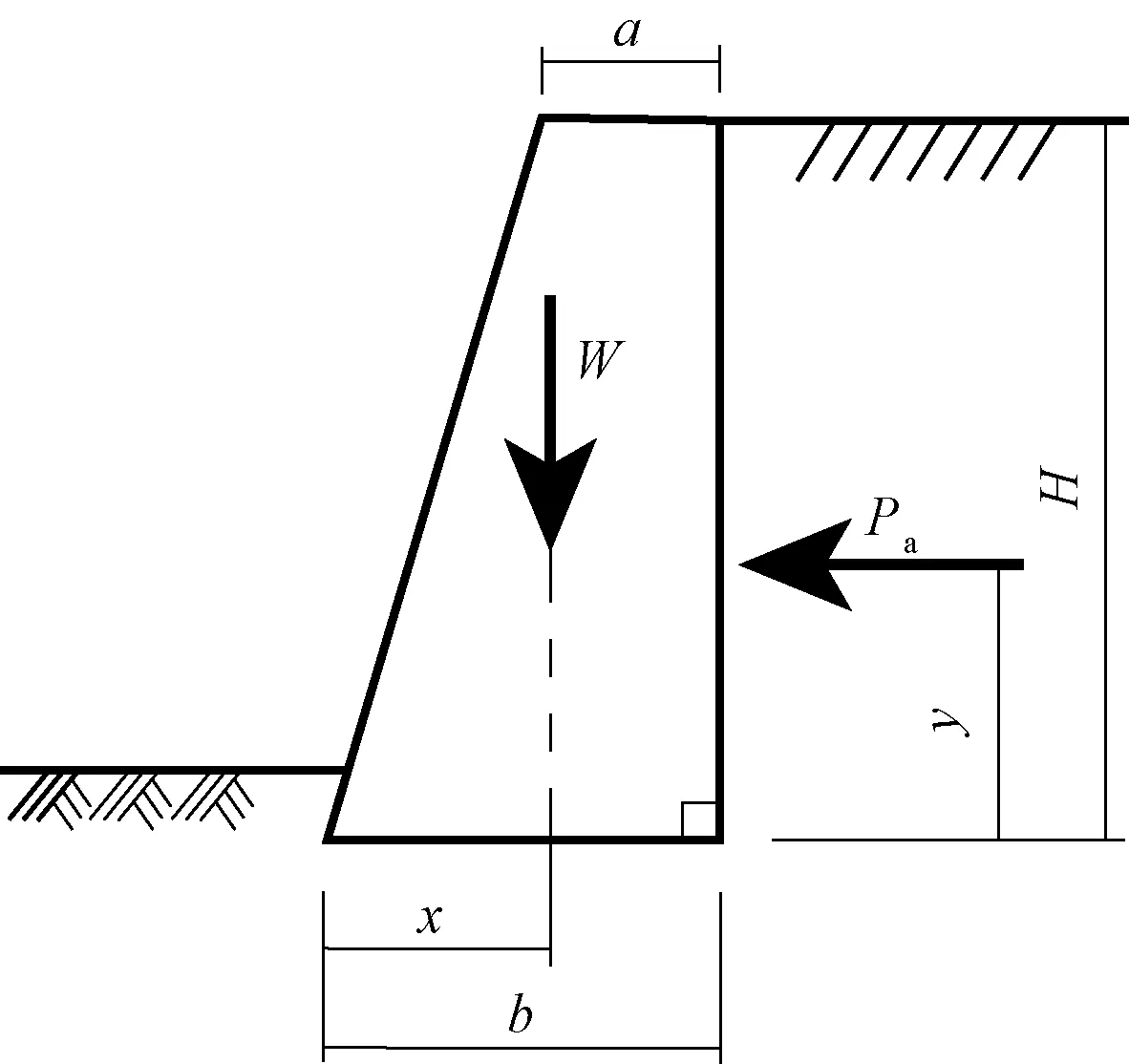
H为挡土墙高；a顶宽；b底宽图1 挡土墙模型示意图Fig.1 Sketch of retaining wall model

根据上述模型，结合相关规范[17-18]，墙自重为

(20)

式(20)：γc为重度。

挡土墙重心至墙趾距离为

(21)

对于三角形分布的总主动土压力作用点距离墙底为

(22)

对于梯形分布的总主动土压力作用点到墙底的距离为

(23)

1.5 考虑填土泊松比的挡土墙稳定性分析模型

参考《建筑地基基础设计规范》GB 50007—2011[17]和《挡土墙设计规范》SL 379—2007[18]，定义挡土墙抗滑稳定性系数与安全系数的比值为有效抗滑安全系数，且有

(24)

式(24)中：ξ填土摩擦系数；fs为安全系数。

同理，记挡土墙有效抗倾覆稳定性系数为

(25)

式(25)中：ft为安全系数。

下面为地基承载力验算。算例中作用在基础底面上的总竖向力等于墙体重W，合力作用点与墙趾距离为

(26)

偏心距e=b/2-x′应满足e

(27)

若要满足地基承载力条件，应同时满足以下两个有效稳定性系数大于1：

(28)

(29)

式中：fa为地基承载力特征值；f′为安全系数，其取值均参考规范。式(24)、式(25)、式(28)和式(29)中任何一个有效稳定性系数小于1，皆判挡土墙失稳，仅当4个判别式同时大于等于1时才可判断挡土墙处于稳定水平。故记挡土墙的稳定性系数

K=min(Ks,Kt,Ka1,Ka2)

(30)

定义墙体稳定性状态用G来表示。当K≥1时，所有稳定性系数均大于规范给定安全系数，挡土墙处于稳定状态，此时G=1；当K<1时，存在至少一个稳定性系数小于安全系数，挡土墙处于失稳状态，此时G=0。

在1.3节主动土压力公式的推导中，由式(12)可得填土泊松比为主动土压力系数的一个自变量，记为Ka=Ka(υ)，将其代入式(16)和式(18)可得ea=ea(υ)，Pa=Pa(υ)，即主动土压力可写为关于泊松比的函数，故挡土墙稳定性系数也为关于填土泊松比的函数，记考虑填土泊松比的挡土墙稳定性分析模型和墙体稳定性状态判别式为

K=K(υ)，G=G(υ)

(31)

通过该模型，墙后填土泊松比对挡土墙稳定性的影响可以被研究。

2 考虑填土泊松比变异性的失稳概率计算模型

为研究墙后填土泊松比变异性对挡土墙失稳破坏概率的影响，在第1节提出的挡土墙稳定性分析模型的基础上，将泊松比视为服从均值为测定值ν0、标准差由变异系CV控制的正态分布的随机变量，结合Monte Carlo法来分析墙后填土泊松比变异性对挡土墙失稳破坏概率的影响。

2.1 随机变量的产生

Monte Carlo法又称随机模拟法，它以概率统计理论为基础，依据大数定律来描述复杂事物的特点。采用MATLAB中的正态分布函数产生相当数量的随机变量νi，记为

(32)

将确定的泊松比ν0作为均值μ，标准差σ=μCV受变异系数CV控制。考虑到土体泊松比的经验取值一般在0.15～0.5[21]，所以生成随机变量时，先随机生成2n个服从正态分布的随机数，再随机筛选出n个符合区间范围的随机数(υ1,υ2,…,υi,…,υn)。

2.2 挡土墙失稳概率计算方法

根据大数定律，在变异系数取CV、均值μ=ν0情况下，将νi分别代入G(νi)进行n次数值模拟，运算结果中共出现m次Gi(μ)=0。当模拟次数n足够大时，所求得失稳概率PCV会趋于稳定，此时可认为挡土墙真实失稳概率为

(33)

整体流程如下。

(1)确定变异系数CV、均值μ，基于Monte Carlo法生成2n个随机数，筛选出n个符合区间的随机泊松比υi,其中，i=1,2,…,n。

(3)根据1.5节公式分别计算Ks、Kt、Ka1、Ka2大小，解出G(νi)。

(4)得到n个Gi(μ)后求解特定CV值下挡土墙的失稳概率PCV。

(5)将步骤(1)～步骤(4)重复λ次，仅当出现的最大概率PjCVmax与最小概率PjCVmin之差小于0.01时，才可进行下个步骤，否则令n=10n，将样本数量n放大10倍后返回步骤(1)重新演算。

(6)当PjCV的值域长度小于0.01时，可认为失稳概率计算值已极接近真实失稳概率。故挡土墙真实失稳概率取所得λ个PjCV的均值，即

(34)

其流程图如图2所示。

3 挡土墙算例的稳定性计算与分析

设挡土墙几何形态如图1所示，其中a=1 m，b=2 m，墙高H=6 m，墙体重度γc=22 kN/m3。墙后填土相关土力学和几何参数如表1所示，部分参数参考文献[22]选定。

表1 填土相关参数统计表Table 1 Parameters of filling soil

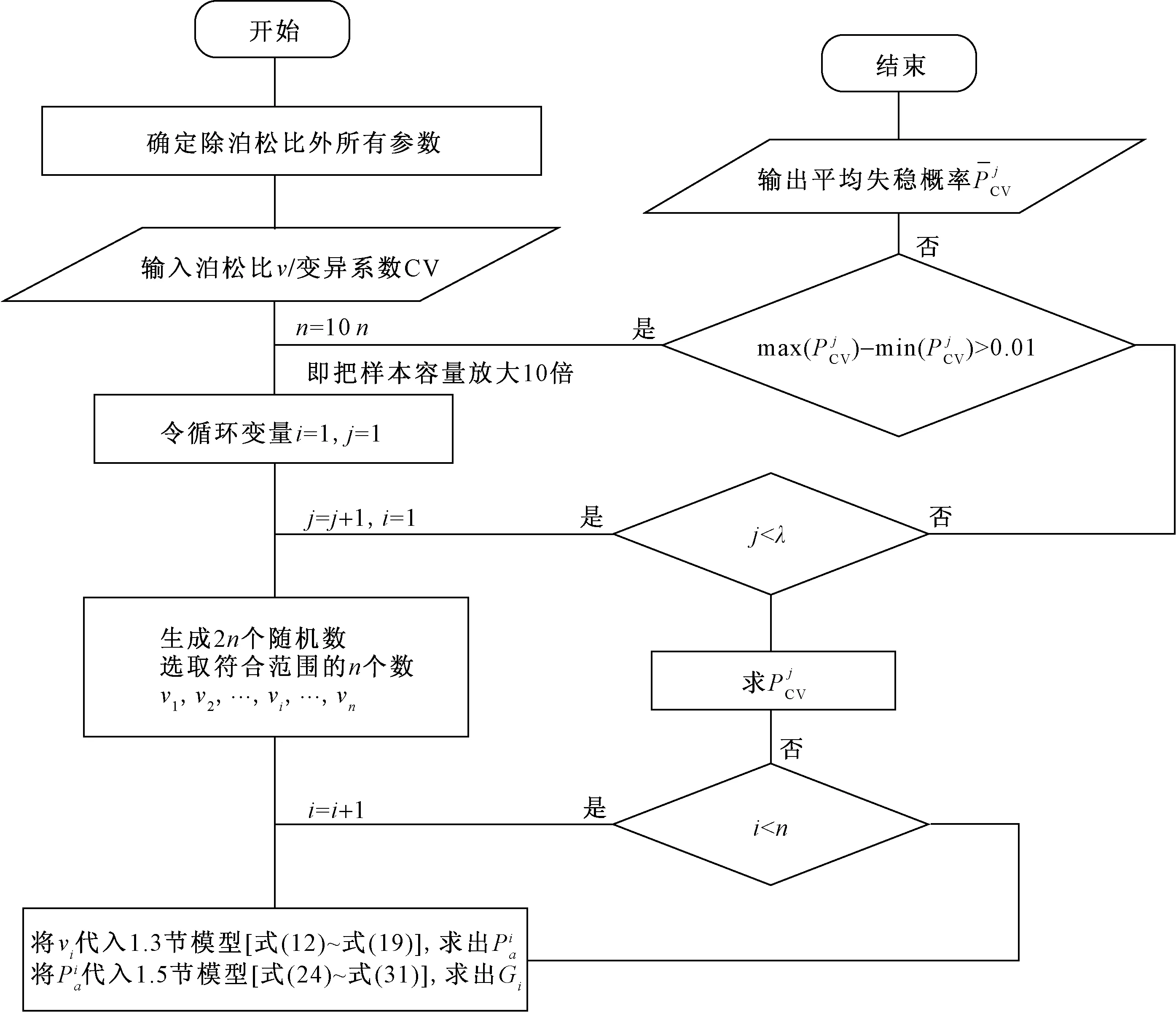
图2 挡土墙可靠度计算流程图Fig.2 Flow chart of reliability calculation of retaining wall

3.1 主动土压力计算式评价

将上述参数代入1.3节基于修正Lade-Duncan准则结合广义Hooke定律的主动土压力计算式中，通过MATLAB平台计算得Ka=0.144,z0=-1.36<0,eaz=15.12 kPa,ea0=2.79 kPa,Pa=45.36 kN/m。

将主动土压力公式计算结果与朗肯土压力计算结果、实测土压力值[22]进行对比，如图3所示。

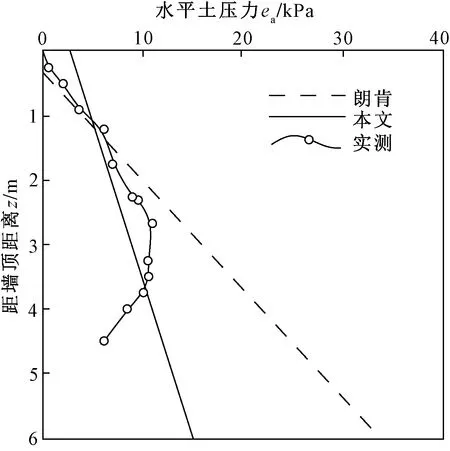
图3 主动土压力曲线对比图Fig.3 Comparison of active earth pressure curves

由图3可见，顶部小范围内，模型计算值略大于朗肯土压力算值，随着距离墙顶距离增大，模型计算值小于朗肯土压力算值，但与实测值更为接近，显示出本模型结果较朗肯土压力具有更好的适用性。其原因在于，朗肯土压力计算中忽略了中主应力σ2的影响，导致其主动土压力系数Ka计算值偏大；而本文模型结合Lade-Duncan准则与Hooke定律，通过引入泊松比ν，考虑了中主应力σ2的影响，使得Ka的取值更加合理，计算结果也表明主动土压力值ea与实测土压力值更为相近。

3.2 考虑填土泊松比的稳定性分析

将3.1节中本文方法的计算结果代入1.5节的稳定性分析模型[式(24)～式(31)]中得

(35)

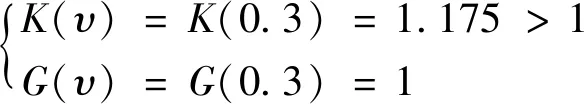
(36)

因此，判得该挡土墙状态为稳定。

3.3 填土泊松比对挡土墙稳定性的影响分析

根据式(31)分析填土泊松比变化对挡土墙稳定性的影响，得到挡土墙稳定性系数K与墙后填土泊松比v的关系曲线如图4所示。

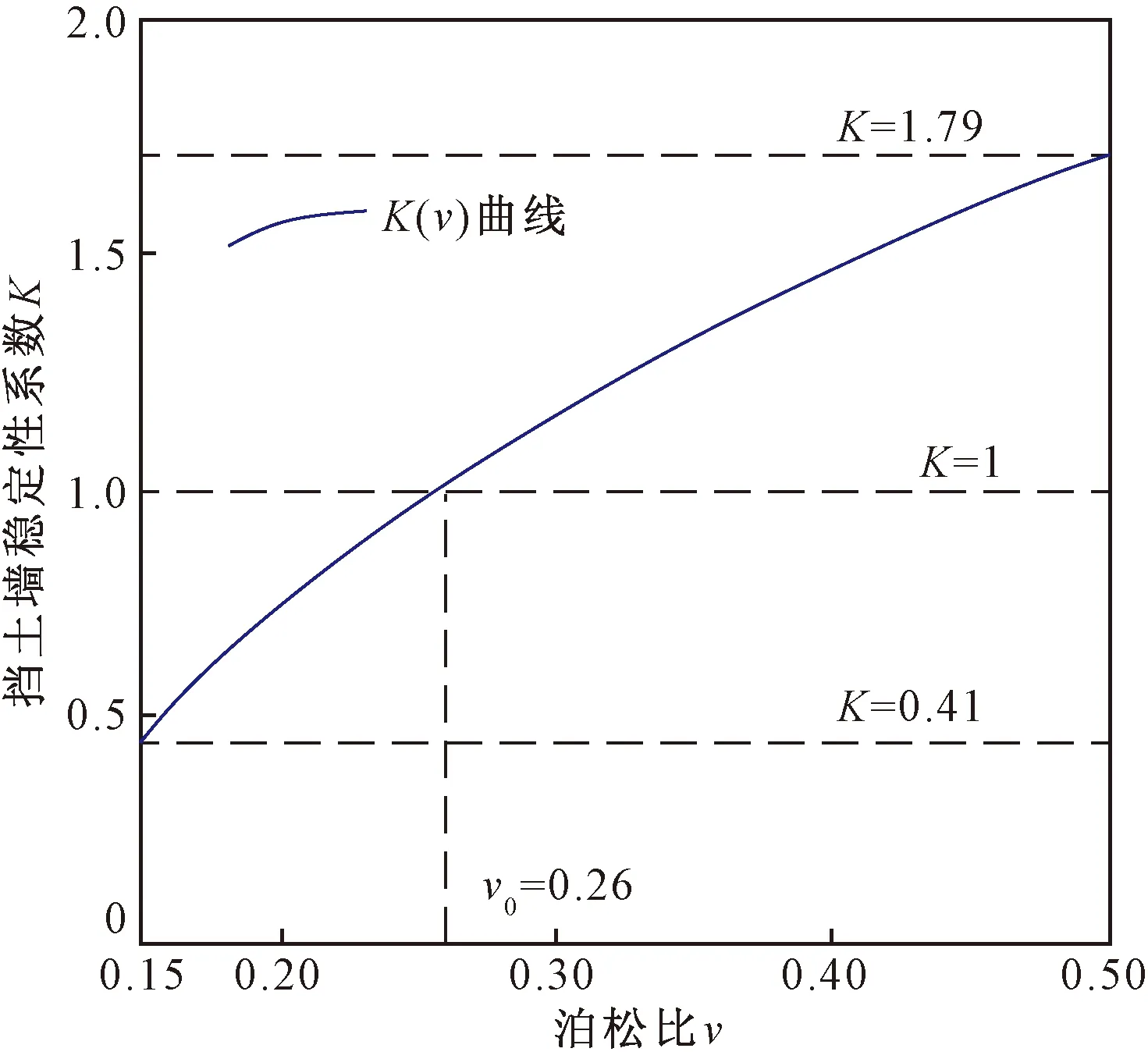
图4 挡土墙稳定系数关于填土泊松比的函数关系曲线Fig.4 Curves of safety factor with Poisson’s ratio of soil

由图4可知挡土墙稳定系数随着墙后填土泊松比的增大而增大。当泊松比ν=0.26时挡土墙的稳定性系数K=1，记此时的临界泊松比为νc。当泊松比ν<νc时，挡土墙稳定系数K<1，当泊松比ν>νc时，K>1。图4表明，在一定取值范围内泊松比取值的不同对墙体有效稳定系数的影响较为明显，泊松比越大，挡土墙有效稳定性越好，也表明了研究微单元土块中主应力水平对墙体稳定性的影响具有重要意义。

4 泊松比变异性对挡土墙失稳概率的影响

4.1 随机样本容量的确定

根据2.2节的分析流程，在结合Monte Carlo法进行挡土墙失稳概率分析前先要随机生成服从正态分析且容量足够的样本。为了确定样本容量，先通过设定泊松比均值μ=ν0=0.3、变异系数CV=0.2来生成随机数来确定样本容量。依据2.1节随机数的产生规则，有

(37)

依据2.2节中失稳概率的分析流程，暂取随机数数量n=10 000，首先基于Monte Carlo法生成20 000个随机数，然后筛选出满足υi∈[0.15,0.5]的10 000个随机数，其分布如图5(a)所示。

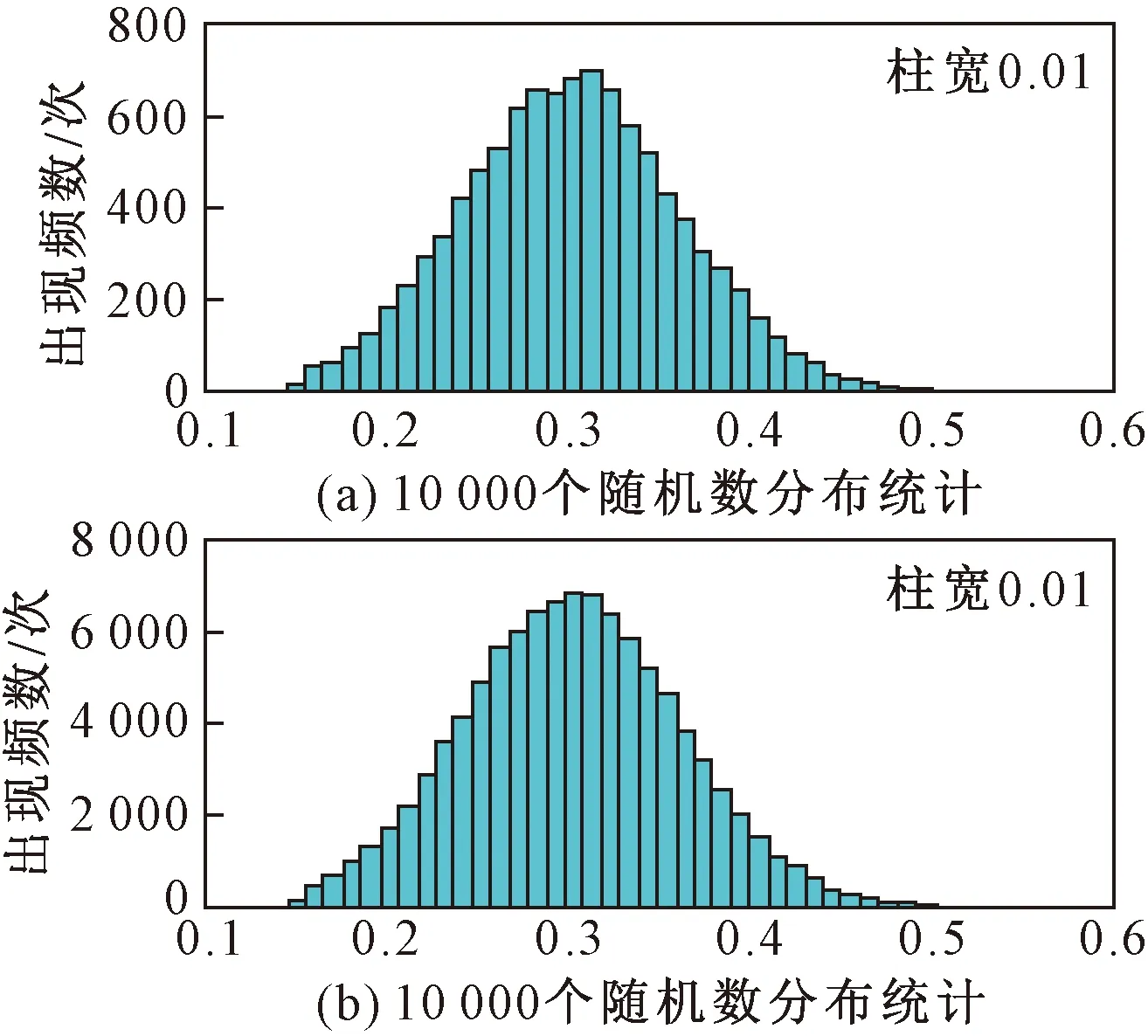
图5 生成随机数分布示意图Fig.5 Sketch of random number distribution

将νi依次通过失稳概率计算求出G(νi)，最后代入式(33)得到CV=0.2时的挡土墙失稳概率PCV=0.2。在MATLAB中循环运算λ次后得到λ个PjCV=0.2。当取λ=100时，发现其值域浮动范围大于0.01，所以认为在计算失稳概率PCV时选取n=10 000样本数量仍不充足，尚不具有代表性。故改令n=100 000，由同样的方法生成100 000个νi，其分布如图5(b)所示。求出λ=100个PjCV=0.2检验得

PjCV=0.2∈(0.231 55,0.238 57)

(38)

PjCV=0.2max-PjCV=0.2min=0.007 02<0.01

(39)

4.2 泊松比变异性对挡土墙失稳概率的影响

现分析该算例中填土泊松比变异性对挡土墙失稳概率的影响。在本文算例中，墙后填土泊松ν=0.3。不考虑泊松比变异性即CV=0时，挡土墙稳定性系数K=1.175。经计算，当生成的随机数属于[0.15,0.5]范围时，随机数样本的变异系数CV的范围属于[0,1)。计算得该范围内泊松比变异系数对失稳概率的影响如图6所示。

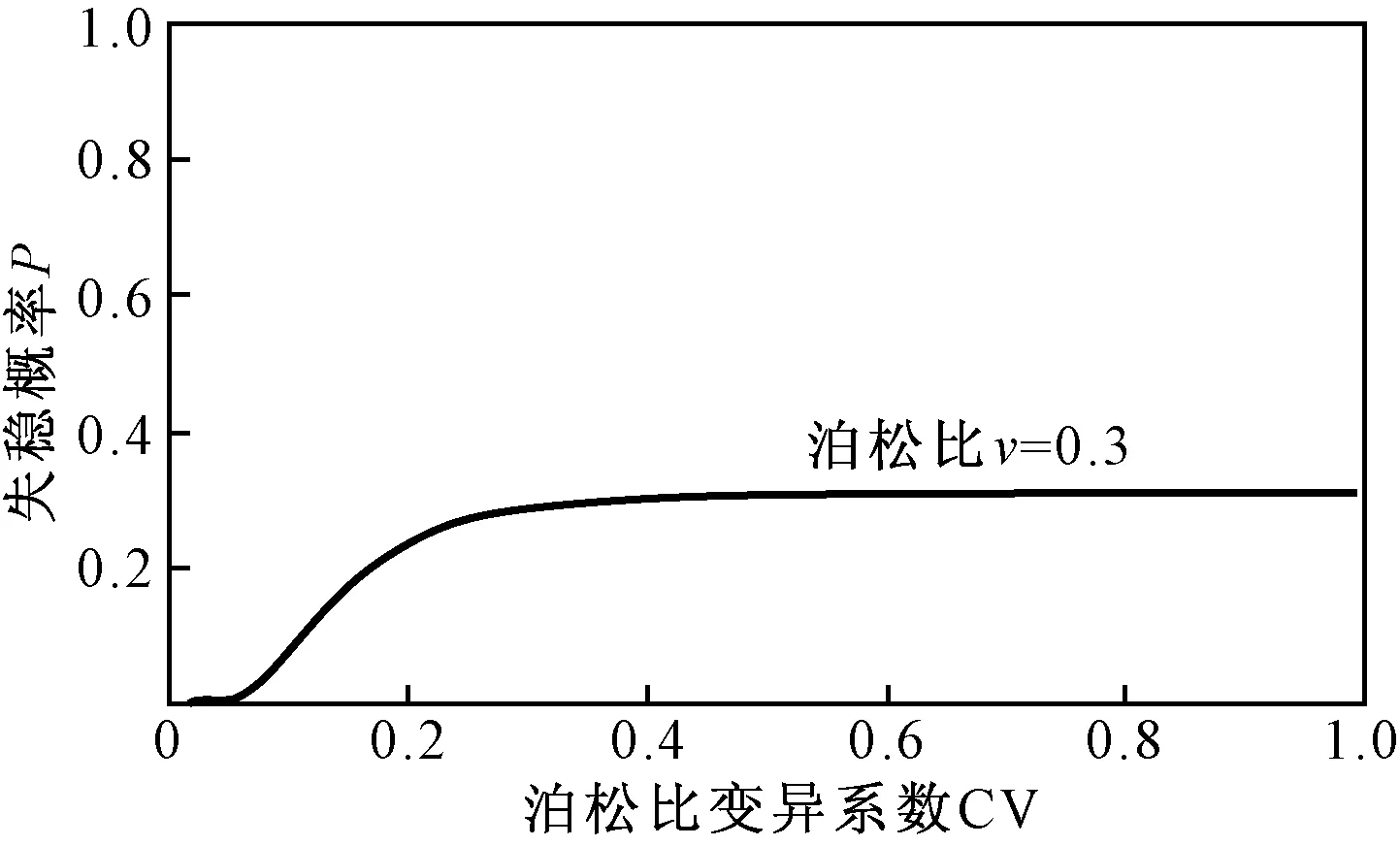
图6 泊松比为0.3时挡土墙失稳概率与变异系数关系曲线Fig.6 Curve of probability of instability of retaining wall with coefficient of variation when Poisson’s ratio is 0.3

由图6可知，在变异系数CV极小的情况下，挡土墙的失稳概率为0。随着变异系数的增加，挡土墙的失稳概率也逐渐增大，并在后期趋于平缓，接近于0.32。

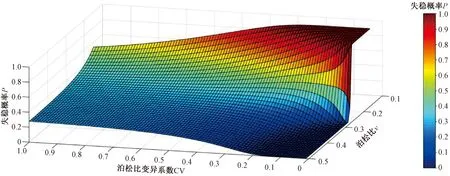
图7 失稳概率关于泊松比和变异系数的函数曲面示意图面Fig.7 Probability diagram of buckling probability versus Poisson’s ratio and coefficient of variation

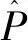
从图7可以更直观地看出，当变异系数一定时，挡土墙的失稳概率大体上随泊松比的增大而降低。

当变异系数CV→0时，失稳概率在ν0=0.26附近处于接近突变的状态。由图4可得挡土墙的稳定性系数与墙后填土的泊松比为正相关关系，且在ν0=0.26时，挡土墙的失稳概率K=1，因此将图4和图7相结合，可将变异系数CV→0时失稳概率在ν0=0.26处突变的现象解读为：变异系数CV越小，填土的泊松比ν0的变异性越小，因此由其计算出的挡土墙稳定性情况越可靠，而结合图4当ν0<0.26时，稳定性系数K<0，当ν0>0.26时稳定性系数K>0，因此判为当ν0<0.26时失稳概率接近1，当ν0>0.26时失稳概率接近0。

随着变异系数的增大，失稳概率在ν0=0.26附近突变的现象逐渐消失，同时失稳概率的最小值(ν0=0.5时)逐渐增大，失稳概率的最大值(ν0=0.15时)逐渐减小，失稳概率关于泊松比的变化曲线随着变异系数的增大由突变性地递增渐变为更加缓和地递增，失稳概率为1或者1的情况也逐渐消失。

当变异系数CV→1时，挡土墙的失稳概率仍随泊松比的增大而降低，此时的变化率最为平缓。当泊松比ν0=0.5时，失稳概率最小(接近0.28)；当泊松比ν0=0.15时，失稳概率最大(接近0.53)。结合图4，说明在CV→1时，即使稳定性系数K=1.79时(泊松比ν0=0.5时)挡土墙仍有大约0.28的可能性失稳，反而稳定性系数K=0.41时(泊松比ν0=0.15时)虽然稳定性系数远小于1，却也仍有约0.47的概率保持稳定状态。

当泊松比ν0>0.26时，挡土墙失稳概率随着变异系数CV的增大而从0开始增大；当泊松比ν0<0.26时，挡土墙失稳概率随着变异系数CV的增大而从1减小。结合图4，说明在挡土墙稳定性系数K>1时，随着墙后填土泊松比变异性的增强，其失稳概率仍会增大，但保持稳定的概率大于失稳的概率；挡土墙稳定性系数K<1时，随着墙后填土泊松比变异性的增强，其失稳概率会减小，即依然保持稳定状态的概率会增大，但保持稳定的概率依然小于失稳的概率。

5 结论

(1)利用修正的Lade-Duncan准则与广义Hooke定律相结合，推导了考虑中主应力的主动土压力计算式，不但将填土泊松比与主动土压力联系在一起，而且对内聚力不为零的填土具较好的适用性，较朗肯土压力对比实际值更为准确。在此基础上，结合相关规范，给出了考虑墙后填土泊松比的挡土墙稳定性分析模型。

(2)基于Monte Carlo法，提出了考虑墙后填土泊松比变异性的挡土墙失稳概率计算模型。模型中泊松比随机数的生成服从均值为测定值、标准差由变异系数控制的正态分布。

(3)结合算例分析了墙后填土泊松比对挡土墙稳定性系数的影响。结果表明：填土泊松比与挡土墙的稳定性系数成正相关关系。填土泊松比越大，挡土墙稳定性越好。

(4)结合算例分析了墙后填土泊松比变异性对挡土墙失稳概率的影响。结果表明：当稳定性系数大于1时，泊松比变异性的增大会引起挡土墙失稳概率的增大，但失稳概率要小于保持稳定的概率；当稳定性系数小于1时，泊松比变异性的增大会引起挡土墙失稳概率的减小，即在泊松比变异性的影响下，虽然计算出的挡土墙稳定性系数小于1，但仍存在保持稳定状态的概率。

(4)在工程实际中，为了更好地把控工程结构的整体稳定性状态、降低挡土墙的失稳概率，应尽量减小墙后填土的不均匀性。在复杂工况下，对挡土墙进行静态或动态稳定性分析时，单靠计算结构稳定性系数的方法并不能完全确保挡土墙结构体处于稳定状态。提出的挡土墙失稳概率分析模型为研究挡土墙的稳定性问题提供了一种新的思路，可以借鉴用于复杂工况中挡土墙可靠度的静态研究，也可用于研究降雨、位移等动态因素作用导致墙后填土差异性增加时的挡土墙稳定性失稳概率分析。