马尔可夫过程在通信物理层中的智能化应用*

张 濛

（中国船舶集团有限公司第七二二研究所 武汉 430205）

1 引言

随着通信技术的不断发展，尤其是5G的研发，一些研究所也成立了5G技术研究室，对通信技术的未来前景提出了更高的要求，即将在各个领域得以广泛应用的人工智能算法应用到通信智能化中，是通信技术发展的大势所趋。

计算机和网络已经成为当今信息时代的核心，现已成为信息社会的命脉和发展知识经济的重要基础。计算机网络是由若干个硬件设备互联而成，这些硬件设备的任务就是要保证系统正常通信。信息的表现形式有多种，各种类型的数据作为基本信息量无差错的传到信宿需要计算机网络来实现。信息化的社会对这些可编程的硬件提出了更高要求。

在五层协议的体系结构中，网络层、运输层、应用层中已经将人工智能算法嵌入资源管理和端系统通信中。现有研究指出将智能核心算法往底层推进，从而让通信更加智能化。但物理层作为分层协议的底层，其作用是要尽可能地屏蔽掉不同传输媒体和通信手段的差异。因为分组信息向下传输到达底层物理层会将原有的数据转化为比特流的形式，不同的传输媒体在传输比特流会存在差别，所以仍处于初探阶段。

一个典型的通信系统由发送端、信道和接收端构成，发送端主要包括信源、信源编码、信道编码、调制等模块；接收端包括信道估计与信号检测、解调、信道解码、信源解码以及信宿等模块。物理层要处理的问题就是信号的调制与解调，包括传信率的大小，传输信号的方向，信号的种类、名称和意义，编码过程等。因为通信系统的信号处理部分，从时域到频域，都遵循着严谨的数学公式，所以若想在物理层中实现智能化，对技术的要求非常高，也难于实现。同时，数学也是人工智能的基石，渗透入各种智能算法中。人工智能就是将数学思维中蕴含的逻辑、建模方法模仿人的思维。其中机器学习中的马尔可夫过程，在实现通信系统物理层的智能化中有一定的应用前景。

2 马尔可夫过程

2.1 马尔可夫过程的无后效性和齐次性

生活中充满了随机事件，比如随风飘落的树叶，一场突如其来的大雨或不期而遇的事故，我们不能改变已经发生的，也不能控制将来，我们能够把握的就是现在。

机器学习中马尔可夫过程即具有只与现在相关的无后效性，其中的马尔可夫链是马尔科夫过程在状态与概率皆离散情况下的特殊情况。当有一组随机序列（Xn，n=0，1，2……）的状态空间E=（1，2，3……），都有第n次的随机状态只受前一次（n-1）状态的影响，见式：P=｛Xn|X1，……，Xn-1｝=P=｛Xn|Xn-1｝，这便是它的无后效性。

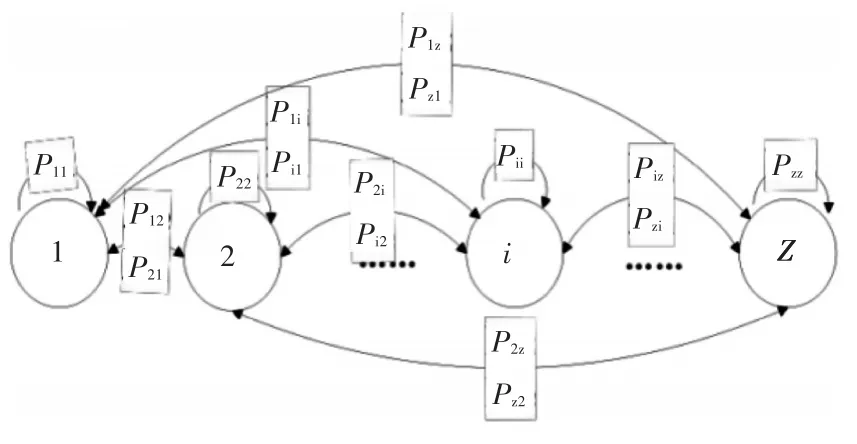
图1 遍历态马尔可夫状态转移过程

同时，马尔可夫过程还具有齐次性和各态遍历性。在马尔可夫链中，若其转移概率与所在位置无关，则称为齐次马尔可夫链。如果一个马尔可夫过程经过有限次状态转移后，不会回到它自身，并且其中任何两个状态不会相互转移，可定义它是各态遍历的。一个各态遍历的马尔可夫过程，无论初始值X0取何值，随着转移次数的增多，随机变量的取值最终都会收敛到平稳分布，这一性质使它可应用到在经济、交通、生物医学、工程建设及无线通信等多领域的智能化技术中。

2.2 马尔可夫的转移概率

马尔可夫过程是从一种状态转移到另一种状态的随机过程，在通信信道建模时，也可描述为转移概率矩阵。因为马尔可夫过程具有在己知当前某一时刻，该通信状态是透明的，马尔可夫过程可以利用统计模型，并且不受先验知识的影响较为准确的预测未来通信可能发生的状态。所以信号在传输过程中，当信道发生异常和衰落等情况发生时，实时获取信号当时的状态，通过马尔可夫状态转移概率矩阵预测下一时刻的通信状态，从而降低或消除了有扰信道中丢失的平均信息量，确保了信息传输的有效性。

因此，将机器学习中的马尔可夫过程应用到通信的智能化中，通信具有连续不间断的特性，对通信信号加以分析处理时需要观察其所处状态，根据某一时刻的状态信息利用转移概率矩阵进行预测，在事件可能发生的集合中选用一个作为决策量。如此循环往复，从而形成决策序列。即在马尔可夫决策过程（Markov Decision Process，MDP）建模时采用马尔可夫假设可以对问题进行简化的同时保留主要关系，针对信道在传输中可能遇到的各种问题，通过马尔可夫过程自适应建模，基于通信系统中物理层的信道估计、信号检测等方面，实现各自模型的智能化适用场景。

3 马尔可夫信源

3.1 编码的不同衡量指标

在通信系统中，接收端收到的信号携带的信息量，要减去有扰信道中不确定的信息量，这些不确定的信息正是因为信道中的干扰和噪声引起的。为了对抗信道中的噪音和衰减，提高抗干扰能力以及纠错能力，保障传输的有效性和可靠性，将通信系统的编码分为信源编码和信道编码。信源编码通过减少信源的冗余，从而增加信息的熵，达到最大的抗干扰性能，提高通信的有效性。信道编码通过增加信源的冗余度减少译码时的错误，从而提高信息传输的可靠性。

在通信系统发送信息时，信源输出是随机性和不确定性的，但又具有一定的关联性，这恰好符合马尔可夫信源的性质。通信过程中将马尔可夫信道状态转移模型应用于信源编码，是从概率角度使其概率达到均匀化，实现统计的独立性，降低信源之间的相关性，使不确定性达到最大，使信源携带的信息量达到最大。

当信源序列中的任何一个消息仅与其前面的一个消息有关联，称它为一阶马尔可夫链，若它与前面m个消息有关联，则称它为m阶马尔可夫链，信源的机制由平稳有限状态的马尔可夫链决定。

其中ui是马尔科夫链的平稳分布，经过多次转移的齐次性和遍历性的马尔可夫信源均趋向平稳分布。即输入的信源，通过建立马尔可夫信道状态转移模型，使其稳定于某一收敛值，达到均方可微或均方可导。

图2 马尔可夫信源转移流程图

3.2 马尔可夫信源数学建模要求

马尔可夫信道状态转移模型，其建模必须满足如下要求。

1）建立遍历态马尔可夫过程：建立通信连接时首先要明确其在正常通信过程中所有可能取到的状态值，在马尔可夫模型的预测下，不论当前时刻信号在传输过程中受到何种影响，均不影响其利用转移概率矩阵对后续可能发生的状态进行概率值预测；

2）状态编码：将1）预测出来的状态值设置合适的阈值大小，进而划分有限个状态区间，对划分出来的状态区间进行编码；

3）构建状态转移约束：对2）编码后，在马尔可夫状态空间的约束下进行遍历，计算其状态转移矩阵。

4 仿真试验

4.1 当前时刻的信号衰落

实验在Matlab2016仿真平台上进行，信号参数的设定：采用频率为900MHz的载波信号，采样频率为15KHz，路径损耗是不变值，为-13dB，信号衰落数据序列服从正态分布N（0，6），在瑞利分布的场景，可以得到瑞利分布的信号衰落概率密度曲线。

无线信道由于在传输过程中受到环境等客观因素的影响，导致通信质量存在很强的随机性，因此，它和有线信道传输方式相比，其搭载的移动通信系统不能或很难预测其信号传输的有效性及可靠性。通过利用数学概率论的统计建模分析，构建先验模型，确立约束函数进而通过马尔可夫决策过程研究信号的发射和接收情况。信号在实际传输过程中，无线的传输环境会受到电磁波的绕射、障碍物的阻碍，致使其需要选择合适的传输路径到达接收端。瑞利衰落信道就是基于传输过程中存在的多种干扰，通过建模分析形成的统计模型。因此，本实验是基于瑞利分布下展开的。

图3 瑞利分布的信号衰落

根据图3结果可知，信源是从一端向外扩散传播，但由于真实场景环境的不确定性导致接收端接收到的信号不是沿着相同路径到达，因此其幅度和相位是随机动态变化的，故造成其包络随机起伏。实验结果符合理论预期。

4.2 马尔可夫状态转移矩阵

图4中，马尔可夫状态转移矩阵为转移步数K从1步到10步的变化时，在瑞利分布场景下观察参数的变化趋势。

图4 瑞利分布场景下马尔可夫状态转移矩阵

可以看出，基于自相关系数计算的马尔可夫状态转移矩阵随着步数增加变化较为平缓，趋向于平稳分布，实验结果较好地验证了马尔可夫决策过程的可行性，以及概率矩阵对于信号经过多步转移后的稳定性，也说明它应用于信号衰落时仍能保持正常通信的可行性。

4.3 马尔可夫状态与传统通信比较

因为信道本身具有随机性和时变性，每一种信道场景需要自适应地选择匹配的马尔可夫模型。本文基于瑞利分布场景，构建了马尔可夫的信道模型，将其与传统通信系统信道作比较，见图5。

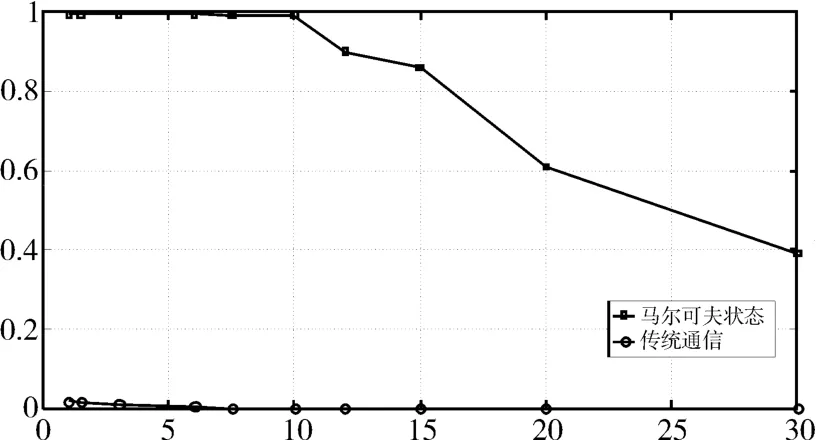
图5 马尔可夫状态与传统通信比较

通过马尔可夫状态与传统通信相比较可看出，马尔可夫状态的信道模型的通信性能要高于传统通信的信道。即当信号发生衰落的情况下，基于马尔可夫过程的信道状态转移模型也能确保通信正常。

表1 马尔可夫转移概率

5 结语

目前，在模拟通信中的语音信号传输中，应用了隐马尔可夫模型（Hidden Markov Model，HMM），把声音模型概率化，成功地运用到语音识别和文字识别中。本文从瑞利分布这个统计模型出发，验证了信号在当前所处时刻的包络情况是符合理论预期的。针对马尔可夫过程数学推理，实验验证了其具有无后效性及平稳性。与传统的通信模型进行对比，具有信号衰减小、失真度低、有效性高、可靠性强等优点。为后续研究计算机网络底层与智能处理算法有机结合提供了实验支撑平台。下一步工作的重点是在前人工作的基础上，创新性的将马尔可夫过程应用到水下救援、工业应急、灾害监测等领域。