双太阳翼GEO 卫星在轨角动量管控方法
2022-01-06洪振强杨立峰陆国平施晨康
洪振强,俞 洁,刘 伟,杨立峰,陆国平,施晨康,赵 辉
(1.上海卫星工程研究所,上海 201109;2.上海航天技术研究院,上海 201109)
0 引言
地球同步轨道(Geosynchronous Earth Orbit,GEO)三轴稳定卫星在轨稳态轮控模式下,通过飞轮吸收环境干扰力矩,保持卫星姿态稳定。在环境力矩的作用下,飞轮角动量存在随时间累积项,需要定期进行角动量卸载,避免飞轮转速饱和。目前,国内外针对航天器环境干扰和动力学特性的在轨辨识已经开展了广泛研究。文献[1]提出了一种利用光压力矩辅助卫星太阳电池翼角度调整进行角动量管控的方法,但该卸载方法仅对对日定向卫星适用。文献[2]设计了一种基于以飞轮极限角动量为参考的零运动力矩分配轮系角动量管控策略,主要目的是避免系统角动量未达到包络面时部分飞轮角动量出现饱和。文献[3]的研究对象限定在采用惯性系为控制基准的航天器角动量管理。文献[4]主要解决引力梯度力矩和气动力矩常值部分带来的角动量积累问题。文献[5]采用引力梯度力矩平衡姿态,设计了基于极点配置的空间站角动量管理控制器。文献[6]对环月地轨道环绕卫星所受重力梯度力矩进行了分析。文献[7]研究了当轨控推力器存在大力矩扰动时系统角动量管控方法。文献[8]研究了角动量管理对卫星轨道的影响,但均不涉及太阳光压力矩。文献[9]研究电推进卫星通过将推力器的指向略微偏离质心来产生控制力矩,完成角动量卸载。文献[10]设计了一种基于气动力矩和模型预测的低地轨道(Low Earth Orbit,LEO)卫星角动量管控算法,但不适用于GEO 卫星。文献[11]用几何方法详细讨论了航天器各表面受晒的情况,推导了不同太阳光入射条件下航天器各面所受到的太阳光压力矩数学模型。文献[12]提出一种精确求取太阳光压有效作用面积的方法。文献[13]对太阳光压力矩与大气阻力力矩的建模与仿真提出了新的方法,准确地对太阳光压力矩与大气阻力力矩进行了估计。文献[14]论述了大型三轴气浮台转动惯量和干扰力矩高精度联合辨识技术,但需要进行主动激励,不便于在轨操作。文献[15]阐述了导航卫星太阳光压建模方法与模型特性分析,主要研究太阳光压对轨道摄动的影响,而不是姿态控制的影响。本文针对对称布局GEO卫星角动量缓慢累积的特点,开展在轨环境力矩辨识和角动量管控研究,可为姿控系统的精细化设计提供参考依据,并以此为基础提出使用3 台飞轮接入闭环控制状态下的角动量管控策略,延长角动量卸载周期。
1 惯性系下角动量模型
静止轨道卫星运行在稳态轮控模式时,通过飞轮吸收外界干扰力矩而保持卫星姿态三轴稳定。由于地球静止轨道高度达到36 000 km,地磁力矩和大气阻尼力矩可以忽略不计,只需要考虑太阳光压和重力梯度力矩的影响。
1.1 太阳光压干扰力矩
关于太阳光压力矩,已经在很多文献中进行了详细的推导和描述。本文的目的是在惯性坐标系中建立太阳光压干扰模型,提取特征参数,为在轨精确辨识奠定基础。单边太阳翼与双边对称太阳翼的太阳光压力矩分析方法一致,其最大区别是太阳光压压心和卫星质心距离存在较大差别。
以双边对称太阳翼为例建立太阳光压干扰力矩模型,如图1 所示。由于角动量守恒定理须在惯性系下描述,因此,首先建立惯性参考系O
X
Y
Z
,其原点O
位于卫星质心,O
X
指向卫星星下点时刻为12:00 对应的飞行方向,O
Y
沿轨道负法向,O
Z
、O
X
和O
Y
满足右手定则。设太阳光压压心在O
X
Y
Z
坐标系中的初始位置矢量为P
=[P P P
],太阳光压法向力为F
=[0 0F
],切向力为F
=[0F
0],力的大小与太阳光入射角α
的关系见文献[1]。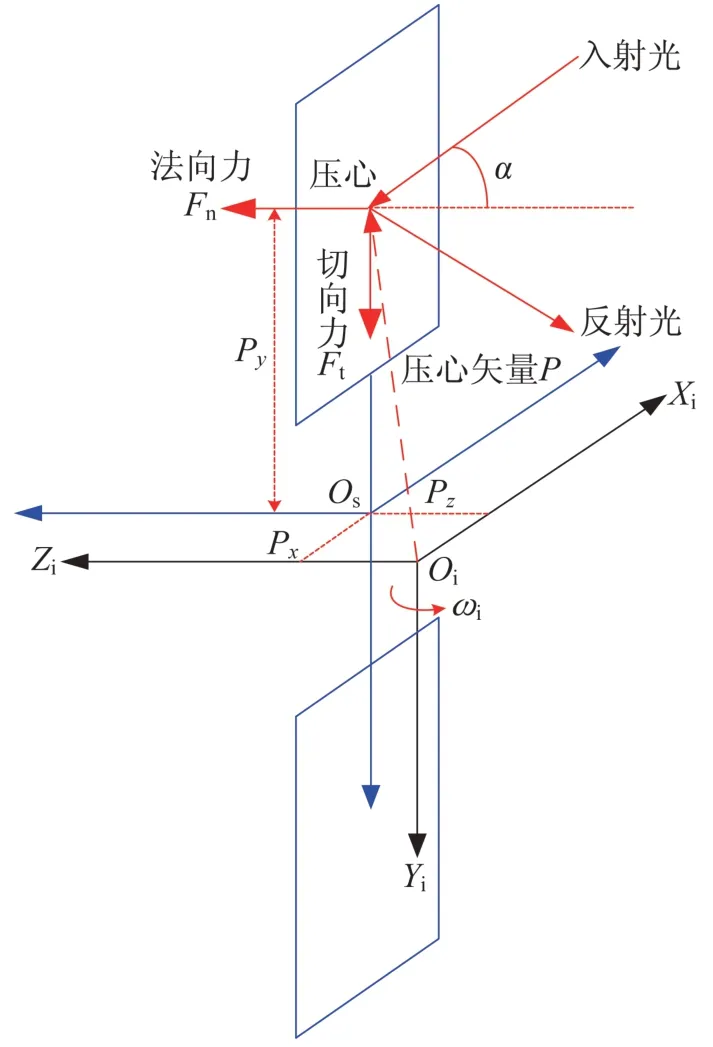
图1 太阳光压作用示意图Fig.1 Schematic diagram of solar pressure effects
设惯性系中太阳光压力矩为T
,其可根据太阳光压力和压心矢量计算得到。由于压心矢量随卫星的轨道运动相对惯性空间旋转,所以先计算时变的压心矢量:

A
(θ
)为绕y
轴的旋转矩阵;旋转角θ
与轨道角速度相关。对于GEO 卫星,可直接由轨道角速度ω
乘以时间得到。进一步可得惯性系下时变的太阳光压力矩T
(t
)为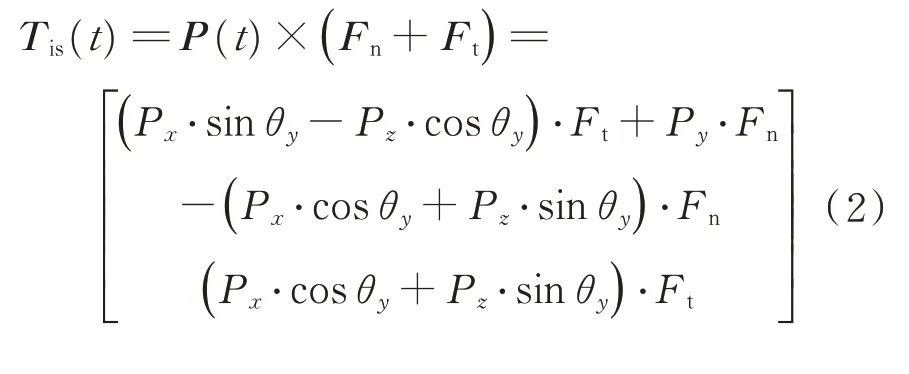
1.2 重力梯度干扰力矩
对于圆轨道卫星,在小姿态情况下,卫星本体坐标系下的重力梯度力矩T
可表示为
φ
、θ
分别为卫星的滚动角和俯仰角。从而可得惯性系中的重力梯度力矩T
(t
)为
φ
≈θ
≈0,因此,式(4)可简化为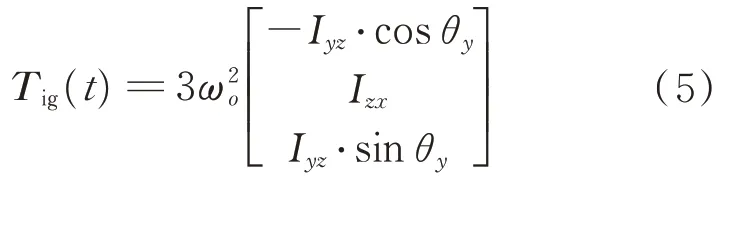
1.3 整星角动量积累模型
根据角动量守恒定理,在惯性系下对干扰力矩进行积分即可得到惯性系中的角动量变化曲线。设惯性系中的角动量为H
=[H
H
H
],有

H
=[H
H
H
],对于GEO卫星,有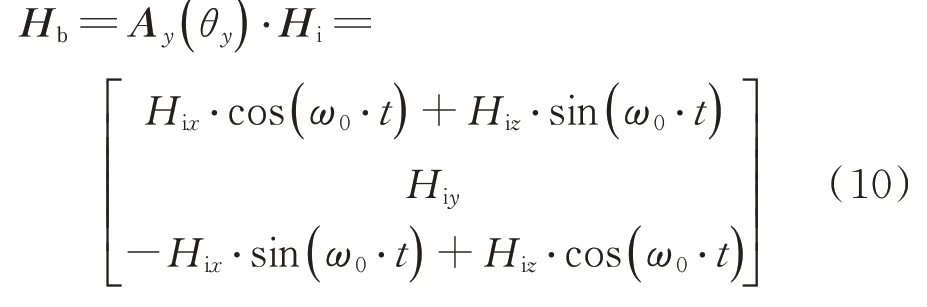
X
、Z
轴合成角动量反映了太阳光压干扰力矩的累积效应,Y
轴角动量反映了重力梯度力矩的累积效应。
表1 GEO 轨道环境干扰力矩分析总结表(相对轨道系零姿态时)Tab.l Analysis summary of GEO orbit environment disturbance torques(relative to the zero attitude of the orbit system)
2 环境干扰力矩辨识
2.1 辨识算法
根据惯性系下的角动量模型式(7)和式(8),其中,式(7)反映了法向太阳光压引起的角动量累积和切向太阳光压及重力梯度力矩引起的角动量交变,式(8)反映了重力梯度力矩引起的角动量累积和切向太阳光压引起的角动量交变。提取特征参数,改写环境干扰角动量累积模型如下:
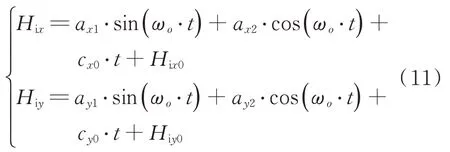
H
、H
分别为X
向和Y
向的初始角动量;特征参数a
、a
、c
、a
、a
、c
分别为
根据上述模型,结合在轨遥测数据,采用最小二乘拟合即可得到各特征系数。根据特征参数,可计算得到法向和切向太阳光压力引起的干扰力矩辨识结果如下:
结果1,法向太阳光压力引起的绕O
X
轴干扰力矩,P
⋅F
=c
;结果2,法向太阳光压力引起的绕O
Y
轴干扰力矩,P
⋅F
=-a
⋅ω
;结果3,切向太阳光压力引起的绕O
Z
轴干扰力矩,P
⋅F
=-a
⋅ω
;
2.2 辨识结果
根据飞轮在轨转速遥测数据,处理得到卫星本体系中和惯性系中的角动量变化曲线如图2 所示。
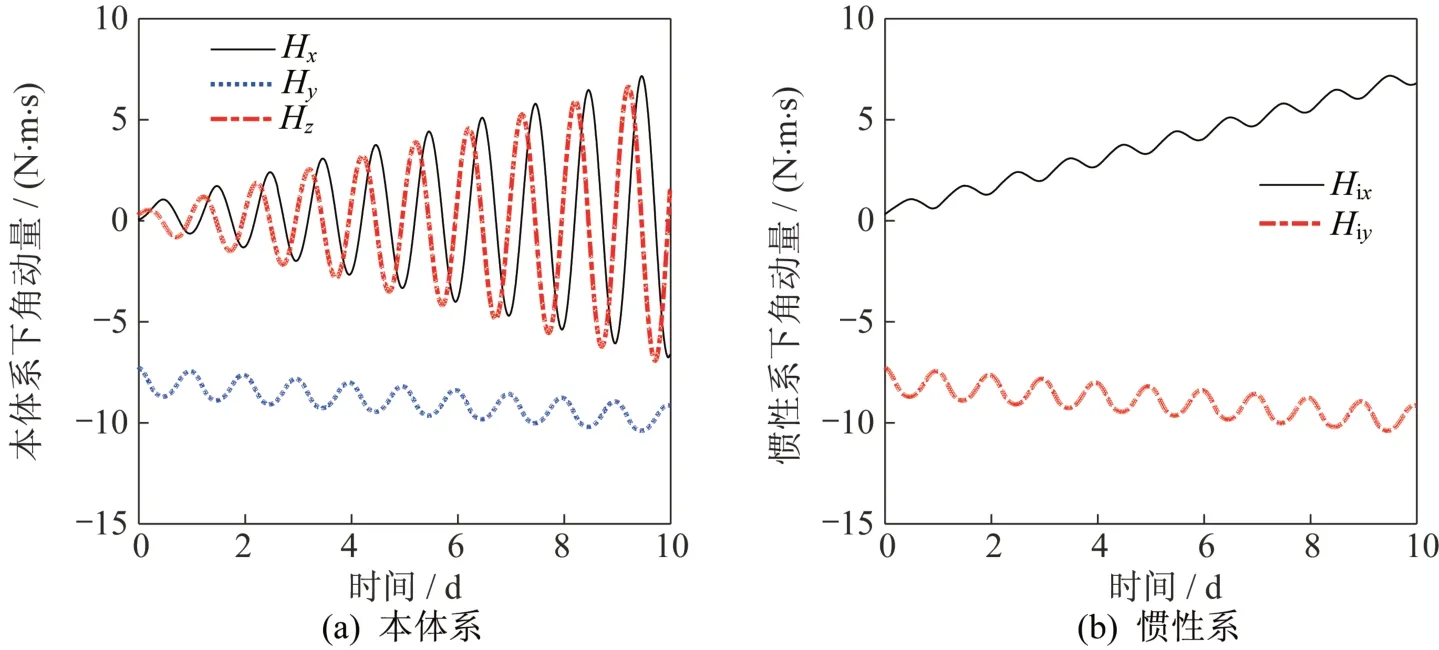
图2 卫星在轨角动量变化示意图Fig.2 Angular momentum change of the on-orbit satellite
对惯性系下的角动量曲线进行拟合,得到拟合结果如图3 和图4 所示。

图3 惯性系下整星角动量拟合结果Fig.3 Fitting results of the angular momentum of the whole satellite in the inertial frame

图4 惯性系下整星角动量拟合残差Fig.4 Fitting residual error of the whole satellite angular momentum in the inertial frame
对应特征参数的数值辨识结果如下:

ω
=7.272 2×10rad/s,根据上述辨识结果可解得,在星下点时刻为12:00 对应的惯性参考系中:结果1,法向太阳光压力引起的绕O
X
轴干扰力矩,P
⋅F
=7.91×10N ⋅m;结果2,法向太阳光压力引起的绕O
Y
轴干扰力矩,P
⋅F
=3.54×10N ⋅m;结果3,切向太阳光压力引起的绕O
Z
轴干扰力矩,P
⋅F
=2.40×10N ⋅m;结果4,切向太阳光压力引起的绕O
X
轴干扰力矩,P
⋅F
=-2.24×10N ⋅m;结果5,绕O
Y
轴重力梯度力矩,T
=3ω
⋅I
=-2.20×10N ⋅m。将上述辨识结果代入式(10),将仿真结果与在轨遥测结果比对,如图5 所示,误差在0.5 N·m·s 以内,表明所建角动量模型和特征参数辨识算法正确且有效。

图5 角动量仿真模型与在轨实际角动量比对示意图Fig.5 Comparison diagram of the angular momentum simulation model and the actual on-orbit angular momentum
3 角动量管控
根据前文的角动量积累机理分析可知,为了延长GEO 卫星在轨的角动量卸载周期,一方面应尽量减小卫星质心与太阳光压压心之间的距离(尤其是在轨道法向);另一方面应尽量减小卫星惯量积I
,从而减小角动量积累的梯度。但是,随着季节的变化和星上剩余燃料的减少,卫星的压心、质心、转动惯量和惯性积均不可避免发生变化。角动量管控的目的是为了延长卸载周期,根据角动量增长趋势设置合理的角动量初值(即对应飞轮初始转速)。因此,有必要对太阳光压力矩和重力梯度力矩进行辨识,并根据辨识结果合理设置飞轮卸载转速(而不是简单卸载到零转速),从而延长角动量卸载周期,提升卫星的在轨应用效能。假设卫星配置三正一斜总共4 台飞轮,正装XYZ
飞轮与卫星本体轴一致,斜装S
飞轮与XYZ
夹角一致,均为54.74°。以上一节的太阳光压力矩和重力梯度力矩辨识结果为例,将其代入整星动力学模型,以飞轮转速超过±2 000 r/min(对应角动量约15 N·m·s)为卸载标志,则可得不同飞轮组合接入状态下,角动量管控前(对应飞轮初始转速均为0 r/min)对应的卸载周期和进行角动量管控后的卸载周期见表2。由表2 可见,角动量管控后使得角动量卸载周期增加1 倍,管控前后的整星角动量累积曲线如图6 和图7 所示。图7 中,从左到右4张图分别展示了4 种接入工况下的飞轮转速变化曲线,每张图的最左侧为设置的飞轮转速初值,最右侧为卸载时对应的飞轮转速,横坐标表示卸载周期。
图6 角动量管控前不同飞轮组合下的飞轮转速变化仿真曲线Fig.6 Simulation curves of flywheel speed changes under different flywheel combinations before angular momentum management and control

图7 角动量管控后不同飞轮组合下的飞轮转速变化仿真曲线Fig.7 Simulation curves of flywheel speed changes under different flywheel combinations after angular momentum management and control
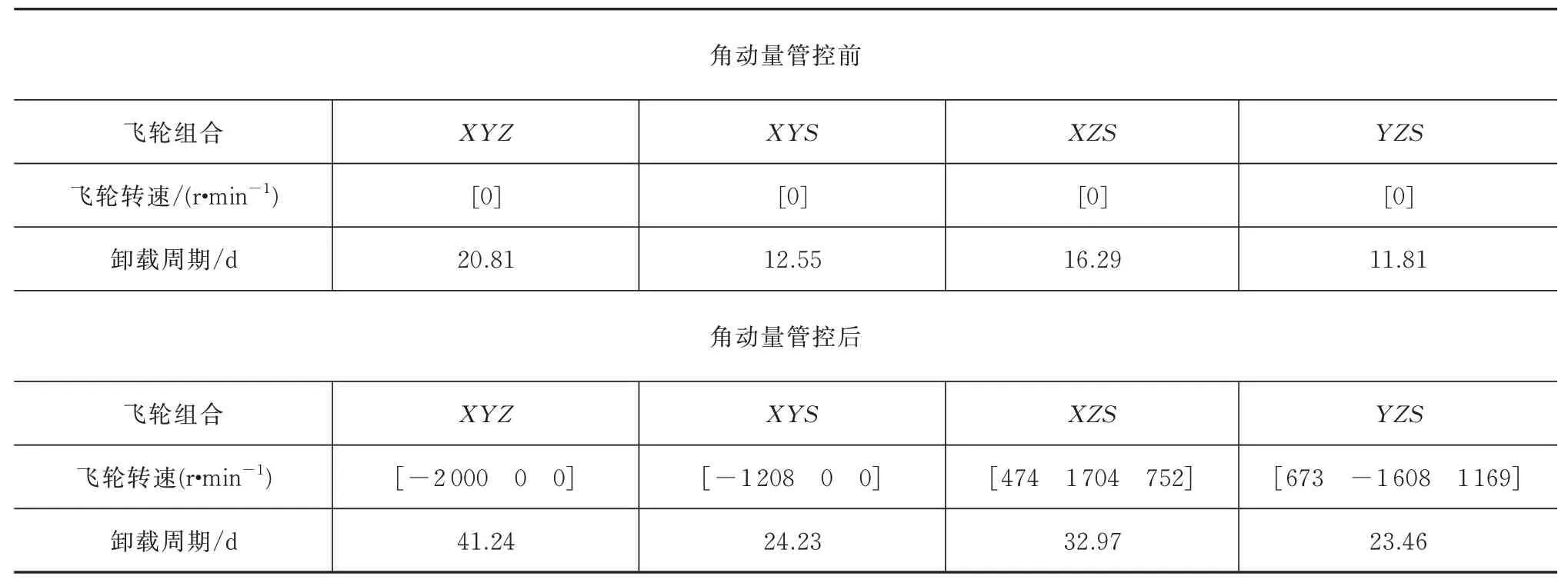
表2 不同飞轮组合下角动量管控前后卸载周期统计表Tab.2 Statistics of unloading periods before and after angular momentum management and control under different flywheel combinations
4 结束语
本文建立了惯性系下双对称太阳电池阵GEO卫星的角动量积累模型,并投影到卫星本体系中,将角动量积累转化为实际飞轮转速的变化。结合实际在轨飞轮转速遥测数据,精准辨识GEO 卫星在轨环境干扰力矩,获取定量结果,并作为输入条件,仿真了不同飞轮组合接入状态下的飞轮转速变化情况。以角动量卸载周期最长为原则,优化了角动量管控策略,将飞轮的角动量卸载周期提升为原来的2 倍,大幅提升卫星在轨的应用效能。
