星箭耦合力学分析中的卫星混合模型研究
2022-01-06赵玉震郭其威唐国安
吴 松,秦 川,刘 松,赵玉震,郭其威,唐国安
(1.复旦大学 航空航天系,上海 200433;2.上海宇航系统工程研究所,上海 201109)
0 引言
为确保航天飞行器能安全可靠地运行,航天飞行器结构不仅要进行静态分析和静力试验,还要进行动力学分析与动态试验,必须采用以结构动力学分析与试验为基础的动态设计技术和动态优化设计技术。为准确预示卫星所承受的载荷和动力学环境,需要卫星研制单位提供代表卫星动力学特性的数学模型给运载火箭研制单位,形成运载-卫星系统级耦合动力学模型,进行星箭耦合系统的动特性响应分析,从而确定卫星所承受的载荷及动力学响应。
用于星箭耦合分析的卫星模型通常以动态子结构方法的缩聚形式提供,即将有限元物理模型内部节点的刚度、质量信息缩聚在边界点上,采用有限元缩聚模型代替物理模型进行力学分析,一方面可以避免输出结构设计的技术细节,起到技术保密的作用;另一方面可以大大减少模型本身的自由度,有利于提高力学分析的计算效率。长期以来,我国卫星特点以“矮胖型”为主,以星箭界面载荷进行结构设计不会造成较严重的过试验。随着航天任务需求的增加,多舱段结构形式的卫星逐步增多,单纯以星箭界面载荷作为卫星结构设计的依据会带来较严重的过设计,需要在星箭耦合分析时提取内部界面的载荷。然而,由于卫星方的动力学模型往往是单纯的缩聚模型,无法直接提取内部界面载荷,需要形成一种适应内部界面载荷提取的卫星缩聚模型生成方法。
动态子结构法是计算大型复杂结构动态特性十分有效的方法,已被广泛应用于航空、航天、舰船、建筑、海洋工程、核工程,以及复杂机械结构的设计与分析,例如运载火箭的建模、星箭耦合分析、大型部件如航天相机、氦气瓶等的建模、复合柔性结构卫星建模,以及卫星的动力学分析。在星箭耦合分析研究方面,文献[15]提出卫星星箭耦合分析模型的二次缩聚方法,将由卫星本体物理模型和天线一次缩聚模型组成的混合模型二次缩聚为满足运载格式的星箭耦合分析出口模型,并与火箭研制方联合开展星箭耦合分析及结果校验,验证了该方法的有效性。文献[10]介绍了采用约束边界模态展开表达式进行星/箭耦合响应分析的方法,通过解析推导可以将整个星/箭耦合结构多自由度方程减缩为仅含星/箭连接界面处自由度的方程,使动力学问题自由度数大大减缩。航天领域的动态子结构方法研究主要集中在缩聚模型生成方法和自由度缩减方面,用于星箭耦合分析的卫星混合模型研究则较少。
本文针对卫星内部界面载荷计算需求,将卫星结构进一步拆分为多个子结构;再基于动态子结构的装配规则,用物理单元将多个子结构进行组装,形成用于耦合分析的卫星混合模型。
1 卫星混合模型生成的基本原理
1.1 卫星子结构划分
假定卫星需要输出一个内部界面载荷,其构型如图1 所示,将卫星划分2 个子结构a
、b
。
图1 卫星构型示意图Fig.1 Schematic diagram of satellite configuration
1.2 子结构缩聚模型生成
对于子结构系统,其振动方程为

定义子结构的外部物理节点,计算其主模态和约束模态为

Φ
为结构的主模态集,即固定界面模态,Φ
=[Φ
… 0];Φ
为结构的约束模态集,Φ
=[Φ
…I
]。将子结构系统的物理坐标采用模态坐标进行表示:

p
为对应主模态的模态坐标;p
为对应约束模态的模态坐标。利用式(3)将子结构振动方程变换到模态坐标p
上,得到
a
的外部节点为A
点和B
点,则子结构a
缩聚模型对应的质量阵和刚度阵分别为
a
与运载火箭连接界面自由度;下标2 为子结构a
与子结构b
连接界面自由度;q
为子结构a
缩聚模型的广义坐标。若将子结构b
的C
点定义为外部节点,则子结构b
截断后的质量阵和刚度阵为
b
与子结构a
连接界面自由度;q
为子结构b
缩聚模型的广义坐标。1.3 子结构间的连接刚度
子结构a
、b
之间的界面连接刚度可等效为6 个方向的刚度,记为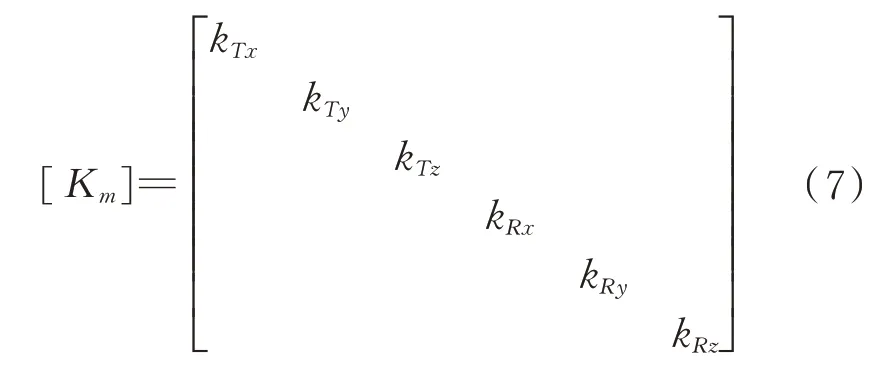
a
、b
连接界面的刚度矩阵为
1.4 子结构装配
若不考虑子结构a
、b
间连接刚度时,对子结构a
、b
进行组装,则卫星综合后质量阵和刚度阵分别为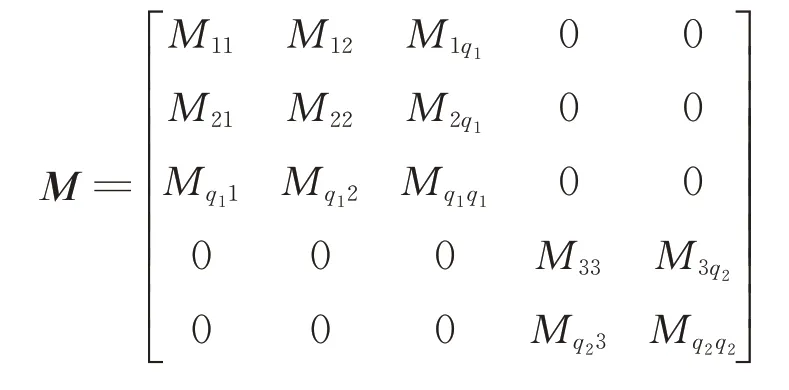

a
和子结构b
间的连接刚度时,卫星综合后的刚度矩阵为
在建立卫星有限元模型时,子结构间的连接刚度可采用弹簧单元或梁单元进行建模。因此,在定义好各子结构的外部节点后,可首先按照动态子结构缩聚理论分别生成各子结构的缩聚模型,再依据各子结构间的连接刚度,按照上述装配关系,组装生成用于星箭耦合分析的卫星混合模型。
该模型中,各子结构的动态特性采用缩聚形式表示,子结构间的连接刚度采用物理模型表示,星箭耦合分析时,可直接输出该物理单元的载荷等响应信息。
2 数值算例
以如图2 所示的包含2 个舱段的典型卫星结构为例,由于其结构呈现出“细长型”的特点,需要进一步分解卫星内部界面载荷等信息,降低卫星“过设计”程度,提升卫星的有效载荷比。

图2 实验舱总体构型Fig.2 Overall configuration of the experimental cabin
卫星总长约20 m,发射质量达22 t,包含舱段1、舱段2。舱段1 质量约13 t,舱段2 质量约9 t。其中,舱段1 与试验夹具、舱段2 之间通过多个螺栓法兰结构进行紧固连接,某一侧连接法兰的局部详细结构如图3 所示。

图3 舱段间的连接法兰Fig.3 Connecting flanges between compartments
建立卫星的有限元分析模型,依据卫星的结构特点,将其划分为子结构a
、b
,2 个子结构间的连接形式通常为螺栓法兰连接结构,考虑到实际工程中往往仅关心界面间的总载荷,而不关心局部连接点的载荷,因而可将各子结构连接界面的点采用多点约束刚性连接至中心点,卫星原始物理模型中,子结构间采用一维弹簧单元或梁单元进行连接,最终划分的子结构如图4 所示。A
、B
点为子结构a
的外部节点,其中,A
点为卫星与运载连接的界面点;B
点为子结构a
上与子结构b
的连接界面点;C
点为子结构b
的外部节点,即子结构b
上,与子结构a
的连接界面点。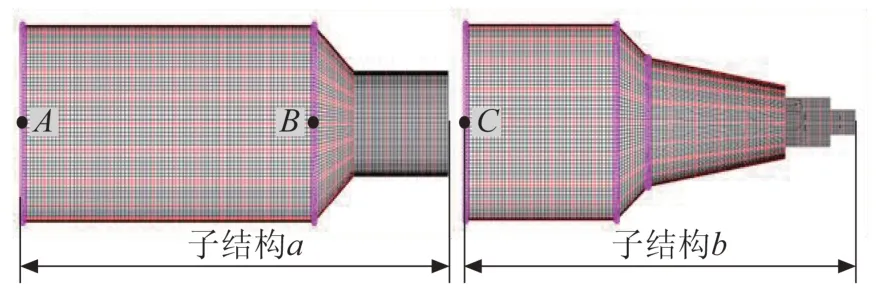
图4 卫星子结构划分Fig.4 Satellite substructure division
依次生成子结构a
、b
的广义刚度矩阵和广义质量矩阵,保留子结构a
、b
之间的一维单元,依据式(10)进行组装,形成缩聚后的卫星混合模型。该模型包含卫星整体的质量阵和刚度阵,依据该质量阵和刚度阵求解其广义特征值,得到混合模型下卫星的模态频率。子结构a、b
保留不同模态阶数时,混合模型下卫星的模态频率计算结果见表1。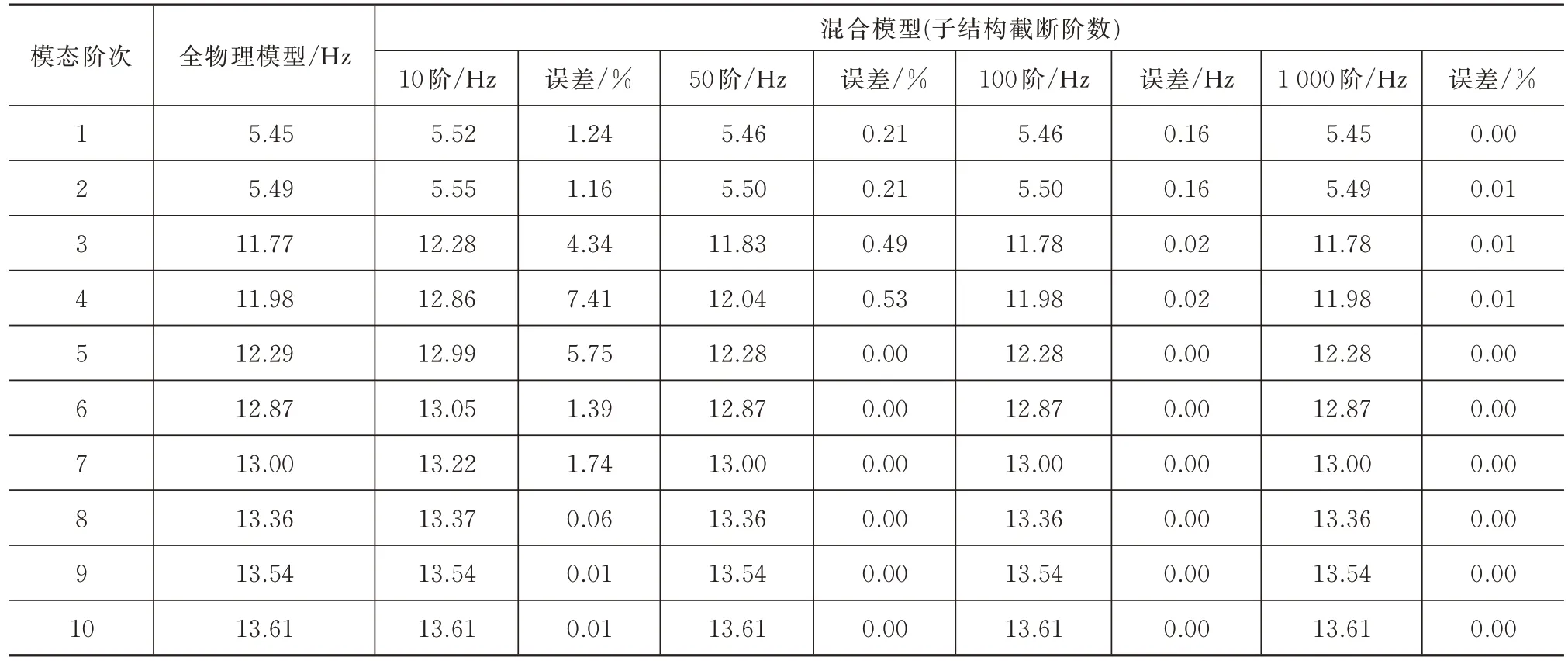
表1 卫星混合模型的计算精度Tab.1 Calculation accuracy of the satellite hybrid model
由表1 可知,子结构在保留较少阶次的模态信息时,即可保证卫星混合模型与全物理有限元模型的计算结果基本一致,说明混合模型能够满足星箭耦合分析的计算精度。而用于星箭耦合分析的卫星模型截断通常在100 阶以上,故卫星的混合模型不会降低星箭耦合分析的精度。此外,表中第5~10 阶频率为子结构局部频率,表明混合模型的精度与子结构的模态截断阶次影响不大。
3 结束语
以某典型卫星结构为例,对“细长型”卫星在星箭耦合分析中其内部界面载荷的计算需求问题,基于子结构缩聚及装配的基本原理,提出了用于星箭耦合分析的卫星混合模型生成方法。该方法在保留了缩聚模型各项优点的基础上,可实现内部界面物理单元的载荷输出,满足工程计算精度的需求,在星箭耦合分析时获取更多响应信息,为卫星设计提供指导。
